Scaling expansions:
universal tool for classification of complex systems
Jan Korbel, Rudolf Hanel and Stefan Thurner


-
Complex systems cover an enormous variety of systems (physics, chemistry, biology, sociology, economy...)
- Different systems have similar statistics
- No united classification
- However, statistical complex systems near the thermodynamic limit (\(N \rightarrow \infty \)) can be characterized by asymptotics of its sample space \(W(N)\)
- Asymptotic behavior can be described by scaling expansion with coefficients corresponding to scaling exponents
- Scaling exponents completely determine universality classes
Asymptotic behavior of \(W(N)\) for \(N \rightarrow \infty\) can be described by the Poincaré asymptotic expansion
$$ f(W(N)) = \sum_{j=0}^n c_j \phi_{j}(N) + \mathcal{O}(\phi_n(N))$$
where \(f(W(N)) = \mathcal{O}(\phi_0(N)) \) and \(\phi_{j+1}(N) = \mathcal{O}(\phi_{j}(N)) \)
Question: What set of functions \( \phi_j(N) \) describes scaling of \(W(N)\)?
Do the coefficients \( c_j \) have any connection to scaling?
Answer: Yes!
We can define an expansion, where the coefficients
\(c_j\) are the scaling exponents of \(W(N)\)
Notation: \(f^{(n)}(x) = \underbrace{f(f(\dots(f(x))\dots))}_{n \ \mathrm{times}} \)
Let us choose \(\phi_j(N) = \log^{(j+1)}(N)\), Then for some \(l\) we can write $$W^{(l)}(N) \equiv \log^{(l+1)}(W(x)) = \sum_{j=0}^n c_j^{(l)} \log^{(j+1)}(N) + \mathcal{O} (\phi_n (N))$$
The coefficients \(c_j^{(l)}\) are the scaling exponents of \(W\)!
We define the set of rescalings \(r_\lambda^{(n)}(x) := \exp^{(n)}(\lambda \log^{(n)}(x) \) )
So \(r_\lambda^{(0)}(x) = \lambda x\), \(r_\lambda^{(1)}(x) = x^\lambda\), \(r_\lambda^{(2)}(x) = e^{\log(x)^\lambda} \), ...
Properties: \(r_\lambda^{(n)} (r_{\lambda'}^{(n)}(x)) = r_{\lambda \lambda'}^{(n)}(x) \), \(r_1^{(n)}(x) = x\)
Leading order scaling: \( \lim_{N \rightarrow \infty}\frac{W^{(l)}(r_\lambda^{(0)}(N))}{W^{(l)}(N)} = \lambda^{\bf c_0^{(l)}} \)
First correction scaling: \( \lim_{N \rightarrow \infty} \frac{W^{(l)} (r_\lambda^{(1)}(N))}{W^{(l)}(N)} \left(\frac{r_\lambda^{(1)}(N)}{N}\right)^{-c_0^{(l)}} = \lambda^{\bf c_1^{(l)}}\)
General rescaling: \( \lim_{N \rightarrow \infty} \frac{W^{(l)}(r_\lambda^{(k)}(N))}{W^{(l)}(N)} \prod_{j=0}^{k-1} \left(\frac{\log^{(j)}(r_\lambda^{(k)}(N))}{\log^{(j)} N}\right)^{-c_j^{(l)}} = \lambda^{\bf c_k^{(l)}}\)
Scaling expansion: \( W(N) \sim \exp^{(l)}\left(\prod_{j=0}^n (\log^{(j)}(N))^{c_j^{(l)}} \right)\)
J.K., R.H., S.T. New J. Phys. 20 093007
Examples
Random walk
- Two possibilities:
step to the left/step to the right
- For \(N\) steps we have
\(W(N) = 2^N\)
possible configurations (paths)
-
Scaling exponents:
- \(l=1\)
- \(c_0^{(1)}=1\)
- \(c_k^{(1)}=0\) for \( k=1,2,\dots\)
Exponential growth:
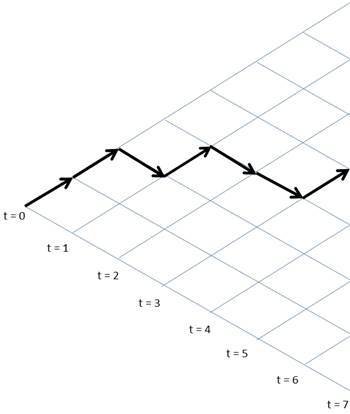
Aging random walk
R.H., S.T. EPL 96 50003, Entropy 15 5324.
Sub-exponential growth (stretched exponential):
- RW with correlations
- After 1 step,
2 steps in the same direction,
3 steps in the same direction....
- Asymptotically we get
\(W(N) \approx 2^{\sqrt{N}/2} \sim 2^{N^{1/2}}\)
-
Scaling exponents:
- \(l=1\)
- \(c_0^{(1)}=1/2\)
- \(c_k^{(1)}=0\) for \( k=1,2,\dots\)
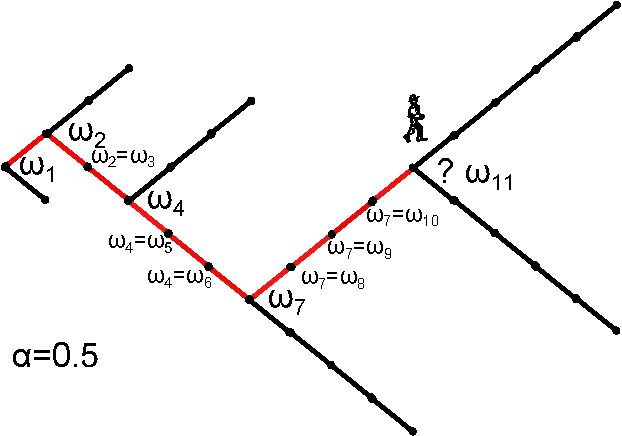
Riemann random walk
Sub-exponential growth:
- another version of correlated RW
- The walker can make decision only for steps which are prime numbers
- Density of prime numbers:
\(\pi(N) \sim N/\log N\)
- \(W(N) = 2^{\pi(N)} \sim 2^{N/\log N}\)
-
Scaling exponents:
- \(l=1\)
- \(c_0^{(1)}=1\)
- \(c_1^{(1)}=-1\)
- \(c_k^{(1)}=0\) for \( k=2,3,\dots\)

Magnetic coins
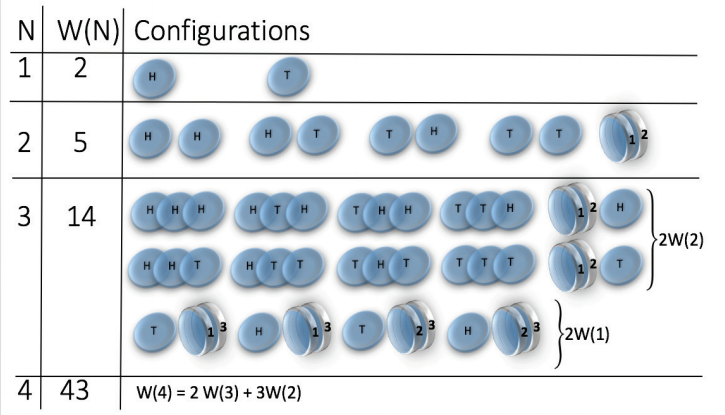
H. Jensen et al. J. Phys. A: Math. Theor. 51 375002
Super-exponential growth:
- \(N\) coins - head or tail
- Coins are magnetic - any two can stick together (1 state)
- \( W(N) \approx N^{N/2} e^{2 \sqrt{N}} \sim e^{N \log N}\)
-
Scaling exponents:
- \(l=1\)
- \(c_0^{(1)}=1\)
- \(c_1^{(1)}=1\)
- \(c_k^{(1)}=0\) for \( k=2,3,\dots\)
Random networks
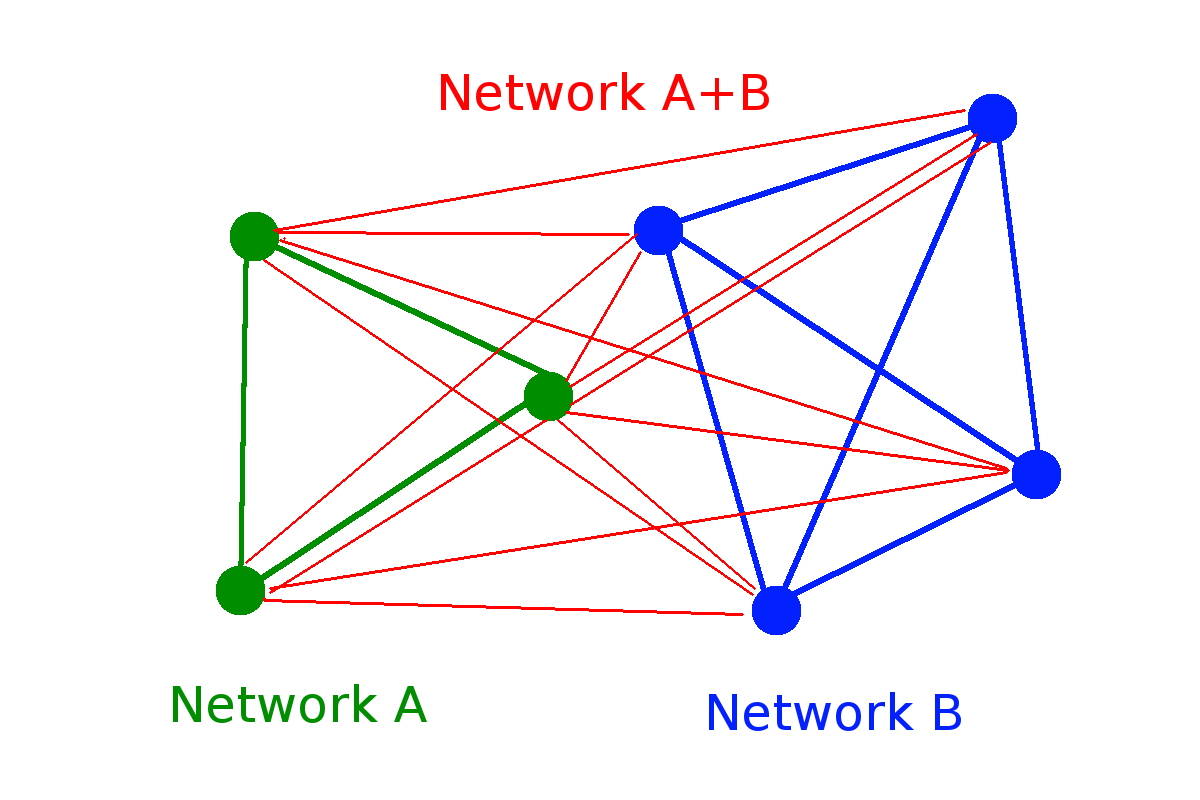
Super-exponential growth (compressed exponential):
- Undirected network with \(N\) nodes has \(\binom{N}{2}\) possible links
- Number of possible networks \( W(N) = 2^{\binom{N}{2}} \sim 2^{N^2}\)
-
Scaling exponents:
- \(l=1\)
- \(c_0^{(1)}=2\)
- \(c_k^{(1)}=0\) for \( k=2,3,\dots\)
Random walk cascades
Super-exponential growth (double-exponential):
- Generalization of RW
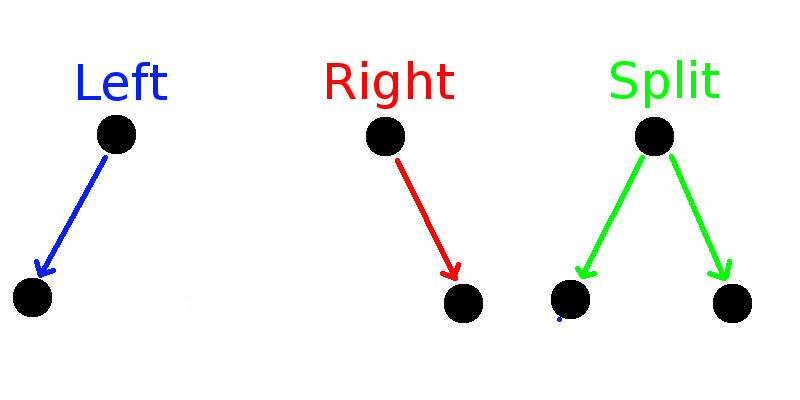
- The walker can go to the left, to the right or split
- After each split, there are two independent walkers
- \(W(N) = 2^{2^N}-1 \sim 2^{2^N}\)
-
Scaling exponents:
- \(l=2\)
- \(c_0^{(2)}=1\)
- \(c_k^{(2)}=0\) for \( k=1,2,\dots\)
Applications
Scaling expansions of extensive entropy
- Scaling expansion can be also found for entropic functionals
- This allows us to consistently define thermodynamics of complex systems and avoid paradoxes from BG thermodynamics
- For microcanonical ensemble ( \(p_i = 1/W\) ) is the scaling expansion given by $$ S(W) \sim \prod_{j=0}^n (\log^{(l+j)} W)^{d_j^{(l)}}$$
- Extensive entropy: \( S(W(N)) \sim N\) for \(N \rightarrow \infty\)
- This gives us relation between \(c_k^{(l)} \) and \(d_k^{(l)} \): $$d_0^{(l)} = 1/c_0^{(l)}$$ $$d_k^{(l)} = - c_k^{(l)}/c_0^{(l)}$$
| Process | S(W) | |||
|---|---|---|---|---|
| Random walk | 0 | 1 | 0 | |
| Aging random walk | 0 | 2 | 0 | |
| Riemann random walk | 0 | 1 | 1 | |
| Magnetic coins | 0 | 1 | -1 | |
| Random networks | 0 | 1/2 | 0 | |
| Random walk cascade | 0 | 0 | 1 |
$$ S(W) \sim \prod_{j=0}^n (\log^{(j)} W)^{d_j}$$
Extensive entropy for example processes
\( \log W\)
\( (\log W)^2\)
\( (\log W)^{1/2}\)
\( \log \log W\)
\( \log W/\log \log W\)
\(d_0\)
\(d_1\)
\(d_2\)
\( \log W \cdot \log \log W\)
Scaling expansions of critical phenomena
- Scaling expansions can determine critical exponents of systems near phase transitions
- Let us have a critical point \(x_c\) where a relevant quantity \(F(x)\) diverges
- Let us write a scaling expansion of \( F \)
in terms of \( \frac{1}{x-x_c} \)
$$ \log F(x) = \sum_{j=0}^n [\log^{(j+1)}(1/(x-x_c))]^{\alpha_j} + \mathcal{O}(\phi_n) $$
- Therefore, we get $$ F(x) \propto (x-x_c)^{-\alpha_0} \log(1/(x-x_c))^{\alpha_1} \log \log(1/(x-x_c))^{\alpha_2}\dots $$
- Typically, only leading-order term is considered, or some other expansions, which do not reflect higher-order rescalings
Information geometry of scaling expansions
- Information geometry applies techniques of diffrerential geometry in statistics and probability theory
- The central quantity of the IG is the information metric \(g_{ij}(p)\)
- The metric is connected to Entropy \(S(P)\) trough Bregman divergence \(D(p||q) = S(p)-S(q) - \langle \nabla S(q),p-q\rangle \) as
- Example: information metric for the first two scaling exponents


\( g_{ij}(p) = \frac{\partial^2 D(p||q)}{\partial q_i \partial q_j}|_{p=q} \)
J.K., R.H., S.T. arXiv:1812.09893
Other possible applications:
- Non-equilibrium thermodynamics
- Dynamics of systems with structures
- ...
We would like to discuss any possible applications, where
- super-exponential processes
- processes with structures
- higher-order scaling exponents
might appear and play a role
Scaling expansions
By Jan Korbel
Scaling expansions
- 340



