Classification of complex systems by their sample-space scaling exponents

Jan Korbel, Rudolf Hanel and Stefan Thurner

Statistical Physics of Complex Systems, 7-11 May 2019, Nordita, Stockholm
this presentation is available online at slides.com/jankorbel
Classification of statistical complex systems
- Many examples of complex system are statistical (stochastic) systems
- Statistical complex systems near the thermodynamic limit \(N \rightarrow \infty \) can be characterized by asymptotics of its sample space \(W(N)\) - space of all possible configurations
-
Asymptotic behavior can be described by
- Coefficients of scaling expansion correspond to scaling exponents
- Scaling exponents completely determine universality classes
-
We can find corresponding extensive entropy
- generalization of (c,d)-entropy \(^\star\)
\(^\star\) R.H., S.T. EPL 93 (2011) 20006
Scaling expansion
Rescaling the sample space
- How the sample space changes when we rescale its size \( N \mapsto \lambda N \)?
- The ratio behaves like \(\frac{W(\lambda N)}{W(N)} \sim \lambda^{c_0} \) for \(N \rightarrow \infty\)
- the exponent \(c_0\) can be extracted by \(\frac{d}{d\lambda}|_{\lambda=1}\): \(c_0 = \lim_{N \rightarrow \infty} \frac{N W'(N)}{W(N)}\)
- For the leading term we have \(W(N) \sim N^{c_0}\).
- Is it only possible scaling? We have \( \frac{W(\lambda N)}{W(N)} \frac{N^{c_0}}{(\lambda N)^{c_0}} \sim 1 \)
- Let us use the other rescaling \( N \mapsto N^\lambda \)
- The we get that \(\frac{W(N^\lambda)}{W(N)} \frac{N^{c_0}}{N^{\lambda c_0}} \sim \lambda^{c_1}\)
- First correction is \(W(N) \sim N^{c_0} (\log N)^{c_1}\)
- It is the same scaling like for \((c,d)\)-entropy
-
Can we go further?
-
We define the set of rescalings \(r_\lambda^{(n)}(x) := \exp^{(n)}(\lambda \log^{(n)}(x) \) )
- \( f^{(n)}(x) = \underbrace{f(f(\dots(f(x))\dots))}_{n \ times}\)
- \(r_\lambda^{(0)}(x) = \lambda x\), \(r_\lambda^{(1)}(x) = x^\lambda\), \(r_\lambda^{(2)}(x) = e^{\log(x)^\lambda} \), ...
- They form a group: \(r_\lambda^{(n)} \left(r_{\lambda'}^{(n)}\right) = r_{\lambda \lambda'}^{(n)} \), \( \left(r_\lambda^{(n)}\right)^{-1} = r_{1/\lambda}^{(n)} \), \(r_1^{(n)}(x) = x\)
-
We repeat the procedure: \(\frac{W(N^\lambda)}{W(N)} \frac{N^{c_0} (\log N)^{c_1} }{N^{\lambda c_0} (\log N^\lambda)^{c_1}} \sim 1\),
- We take \(N \mapsto r_\lambda^{(2)}(N)\)
- \(\frac{W(r_\lambda^{(2)}(N))}{W(N)} \frac{N^{c_0} (\log N)^{c_1} }{r_\lambda^{(2)}(N)^{c_0} (\log r_\lambda^{(2)}(N))^{c_1}} \sim \lambda^{c_2}\),
- Second correction is \(W(N) \sim N^{c_0} (\log N)^{c_1} (\log \log N)^{c_2}\)
Rescaling the sample space II
Rescaling the sample space III
- General correction is given by \( \frac{W(r_\lambda^{(k)}(N))}{W(N)} \prod_{j=0}^{k-1} \left(\frac{\log^{(j)} N}{\log^{(j)}(r_\lambda^{(k)}(N))}\right)^{c_j} \sim \lambda^{\bf c_k}\)
-
Possible issue: what if \(c_0 = +\infty\)? Then \(W(N)\) grows faster than any \(N^\alpha\)
- We replace \(W(N) \mapsto \log W(N)\)
- The leading order scaling is \(\frac{\log W(\lambda N)}{\log W(N)} \sim \lambda^{c_0} \) for \(N \rightarrow \infty\)
- So we have \(W(N) \sim \exp(N^{c_0})\)
- If this is not enough, we replace \(W(N) \mapsto \log^{(l)} W(N)\) so that we get finite \(c_0\)
- General expansion of \(W(N)\) is $$W(N) \sim \exp^{(l)} \left(N^{c_0}(\log N)^{c_1} (\log \log N)^{c_2} \dots\right) $$
J.K., R.H., S.T. New J. Phys. 20 (2018) 093007
$$W^{(l)}(N) \equiv \log^{(l+1)}(W(x)) = \sum_{j=0}^n c_j^{(l)} \log^{(j+1)}(N) + \mathcal{O} (\phi_n (N))$$
Scaling Expansion
- Previous formula can be expressed in terms of Poincaré asymptotic expansion
- Coefficients of the expansion are scaling exponents and can be calculated from:
$$ c^{(l)}_k = \lim_{N \rightarrow \infty} \log^{(k)}(N) \left( \log^{(k-1)} \left(\dots\left( \log N \left(\frac{N W'(N)}{\prod_{i=0}^l \log^{(i)}(W(N))}-c^{(l)}_0\right)-c^{(l)}_1\right) \dots\right) - c^{(l)}_k\right)$$
Extensive entropy
- We can do the same procedure with entropy \(S(W)\)
- Leading order scaling: \( \frac{S(\lambda W)}{S(W)} \sim \lambda^{d_0}\)
-
First correction \( \frac{S(W^\lambda)}{S(W)} \frac{W^{d_0}}{W^{\lambda d_0}} \sim \lambda^{d_1}\)
- First two scalings correspond to \((c,d)\)-entropy for \(c= 1-d_0\) and \(d = d_1\)
- Scaling expansion of entropy $$S(W) \sim W^{d_0} (\log W)^{d_1} (\log \log W)^{d_2} \dots $$
-
Requirement of extensivity \(S(W(N)) \sim N\) determines the relation between \(c\) and \(d\) :
- \(d_l = 1/c_0\), \(d_{l+k} = - c_k/c_0\) for \(k = 1,2,\dots\)
EXAMPLES
| Process | S(W) | |||
|---|---|---|---|---|
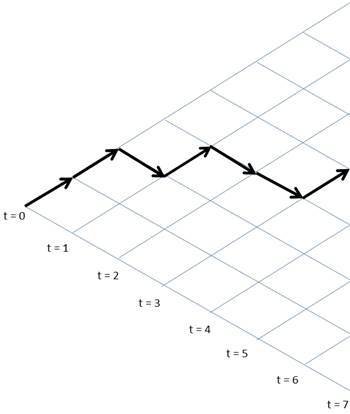
| Random walk |
0 |
1 |
0 |
|
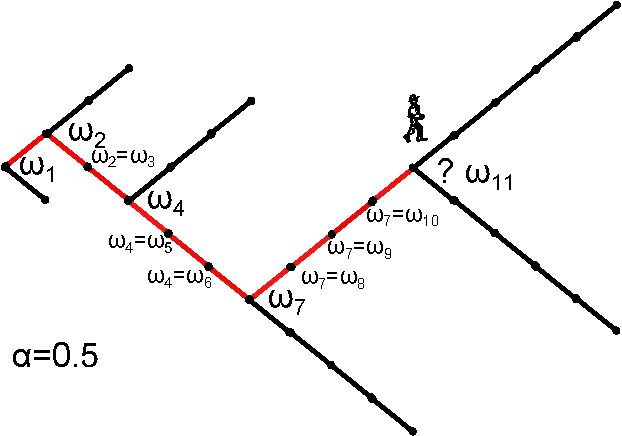
| Aging random walk |
0 |
2 |
0 |
|
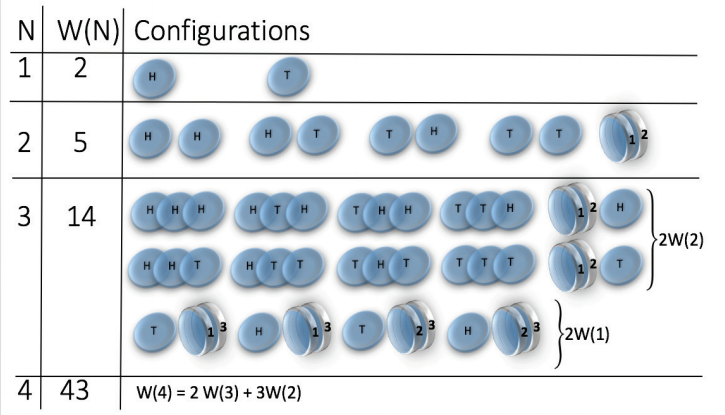
| Magnetic coins * |
0 |
1 |
-1 |
|
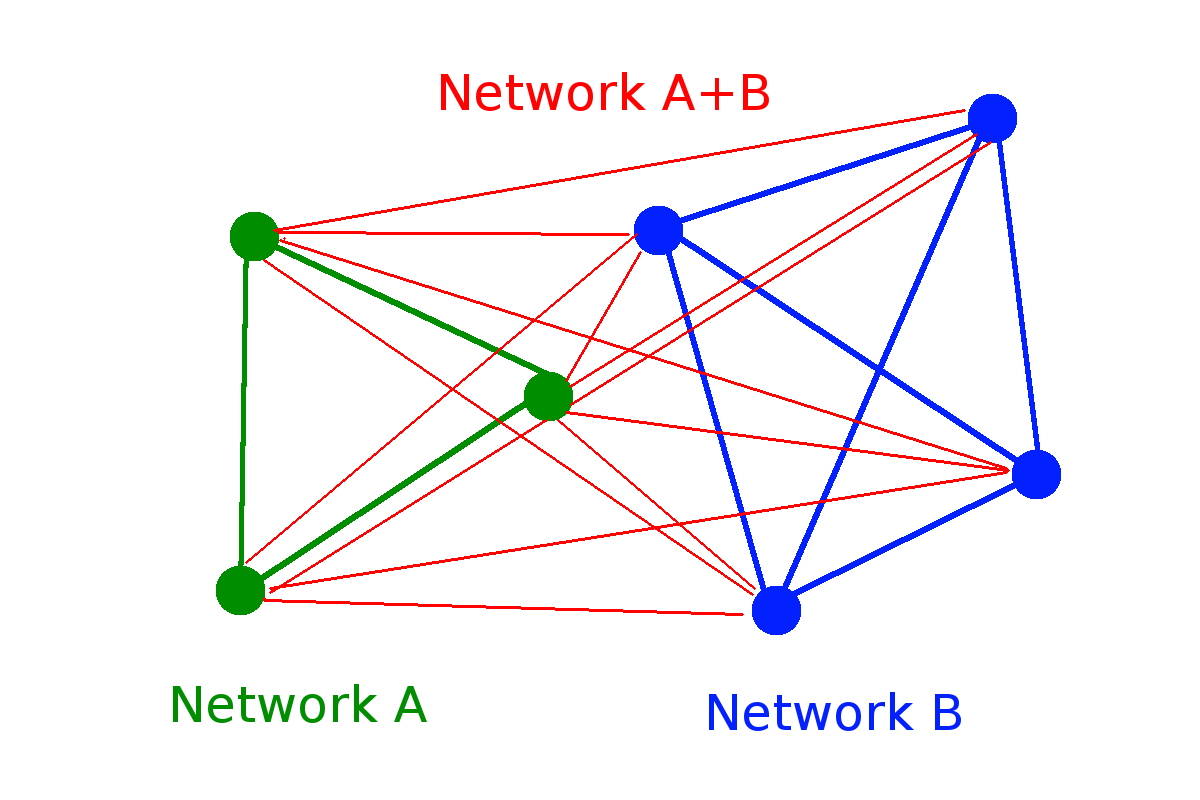
| Random network |
0 |
1/2 |
0 |
|
| Random walk cascade |
0 |
0 |
1 |
\( \log W\)
\( (\log W)^2\)
\( (\log W)^{1/2}\)
\( \log \log W\)
\(d_0\)
\(d_1\)
\(d_2\)
\( \log W/\log \log W\)
* H. Jensen et al. J. Phys. A: Math. Theor. 51 375002
\( W(N) = 2^N\)
\(W(N) \approx 2^{\sqrt{N}/2} \sim 2^{N^{1/2}}\)
\( W(N) \approx N^{N/2} e^{2 \sqrt{N}} \sim e^{N \log N}\)
\(W(N) = 2^{\binom{N}{2}} \sim 2^{N^2}\)
\(W(N) = 2^{2^N}-1 \sim 2^{2^N}\)

Parameter space of \( (c,d) \) - entropy
How does it change for one more scaling exponent?
R.H., S.T. EPL 93 (2011) 20006
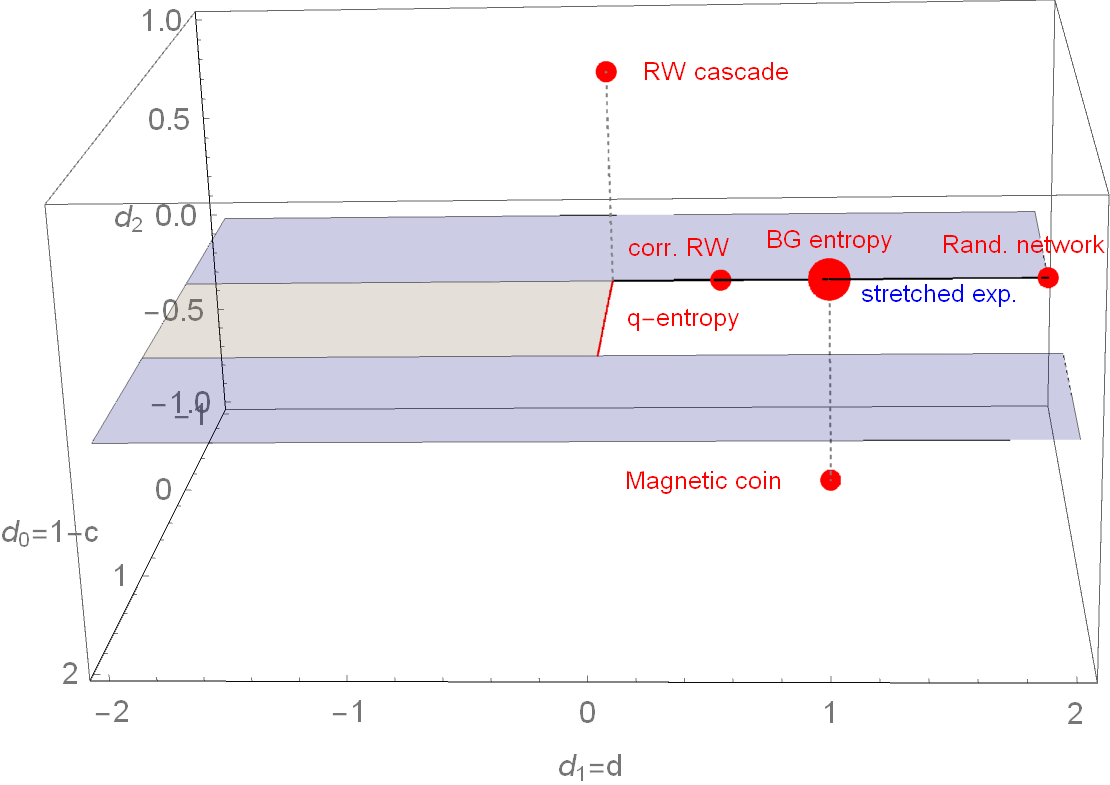
Parameter space of \( (d_0,d_1,d_2) \)-entropy
To fulfill SK axiom 2 (maximality): \(d_l > 0\), to fulfill SK axiom 3 (expandability): \(d_0 < 1\)
Perspectives
Fields of possible applications of scaling expansions:
- Non-equilibrium thermodynamics
- Information geometry\(^\star\)
- Critical phase transitions
- Information theory (Shannon-Khinchin axioms\(^\dag\))
- Statistical inference (Shore-Johnson axioms\(^\ddag\))
- Super-exponential processes
- Processes with structures
- ...
\(^\star\) J.K., R.H., S.T. Entropy 21(2) (2019) 112
\(^\dag\) P. Tempesta, Proc. R. Soc. A 472 (2016) 2195
\(^\ddag\) P.J., J.K. Phys. Rev. Lett. 122 (2019), 120601
References
- J.K., R.H., S.T. Classification of complex systems by their sample-space scaling exponents, New J. Phys. 20 (2018) 093007
- H. Jensen, R. H. Pazuki, G. Pruessner, P. Tempesta, Statistical mechanics of exploding phase spaces: Ontic open systems, J. Phys. A: Math. Theor. 51 375002
- R.H., S.T. A comprehensive classification of complex statistical systems and an axiomatic derivation of their entropy and distribution functions, EPL 93 (2011) 20006
- P. Tempesta, Formal groups and Z-entropies, Proc. R. Soc. A 472 (2016) 2195
- P.J., J.K. Maximum Entropy Principle in Statistical Inference: Case for Non-Shannonian Entropies, Phys. Rev. Lett. 122 (2019), 120601
- J.K., R.H., S.T. Information Geometric Duality of ϕ-Deformed Exponential Families, Entropy 21(2) (2019) 112
I am excited to discuss any possible application
of scaling expansions
during the welcome reception or later
ENJOY THE welcome reception!
Classification of complex system by their sample-space scaling exponents
By Jan Korbel
Classification of complex system by their sample-space scaling exponents
Classification of complex systems by their sample-space scaling exponents
- 376



