Homophily-Based Social Group Formation

in a Spin Glass Self-Assembly Framework

in collaboration with

Simon Lindner

Tuan Pham

Rudolf Hanel

Stefan Thurner

Journal Ref.: Phys. Rev. Lett. 130, 057401 

Slides available at: www.slides.com/jankorbel

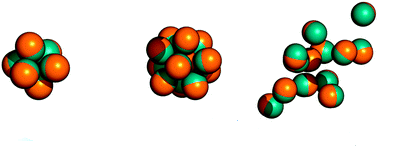
Graphical abstract

Self-assembly

Spin glasses

Social group formation

1. Thermodynamics of self-assembly

• Many systems form structures: molecules of atoms, clusters of colloidal particles, (bio)polymers, or even social groups
• We study the thermodynamics of structure-forming systems
• For small systems, we get a correction to Shannon entropy
• We apply the results to several physical systems

Motivation

Boltzmann's formula for entropy

\( S = k \cdot \log W\)

Typically, \(W = \frac{n!}{n_1!\dots n_j!}\)

Then \(S = - \sum_j p_j \log p_j\)

where \(p_j = n_j/n\) 

Toy model - magnetic coin model

We consider a coin with two states: head             and tail

The coins are magnetic and can stick together 

How many states we get for N coins?

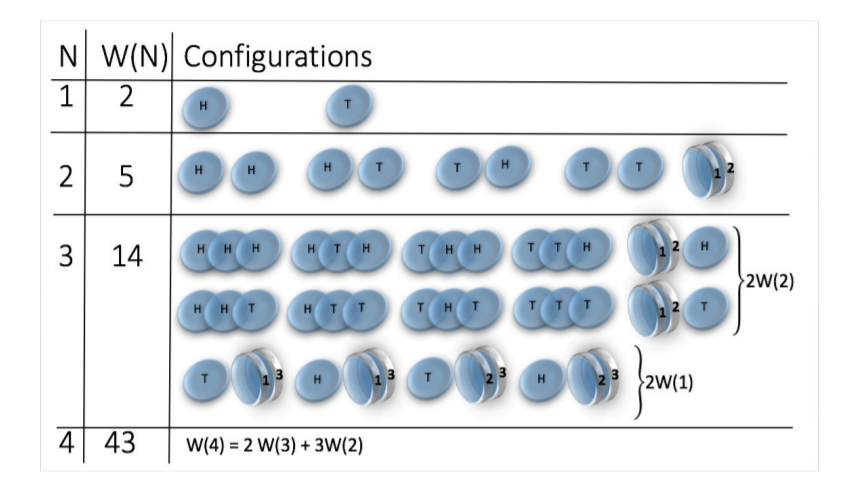
\(W(N) \sim N^N\)

(non-magnetic coins \(W(N) = 2^N\))

picture taken from: H. J. Jensen et al 2018 J. Phys. A: Math. Theor. 51 375002

Multiplicity and entropy

of structure-forming systems

Boltzmann entropy formula: \(S(n_i) = k_B \log W(n_i)\) 

where \(W\) is multiplicity

(number of microstates corresponding to a mesostate \(n_i\))

Microstate: state of each particle; if more particles are bound to a molecule, then the state of each molecule

Mesostate: how many particles and/or molecules are in a given state

Example: magnetic coin model: 3 coins, magnetic

        microstates                       mesostate                 multiplicity

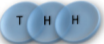
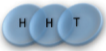
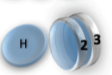
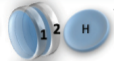
2 x           1x

1 x          1x

3

3

How to calculate a multiplicity?

1. Consider a mesostate
2. Make all permutations of particles
3. Some microstates are overrepresented - calculate how many permutations belong to the same microstate

Examples

2 x           1x

1 x          1x

1    1   2   2    3   3

2   3   1   3    1    2

3   2   3   1    2    1

1    1   2   2    3   3

2   3   1   3    1    2

3   2   3   1    2    1

= (1,2,3) , (2,1,3)

= (1,3,2) , (3,1,2)

= (2,3,1) , (3,2,1)

= (1,2,3) , (1,3,2)

= (2,1,3) , (2,3,1)

= (3,1,2) , (3,2,1)

General formula for multiplicity

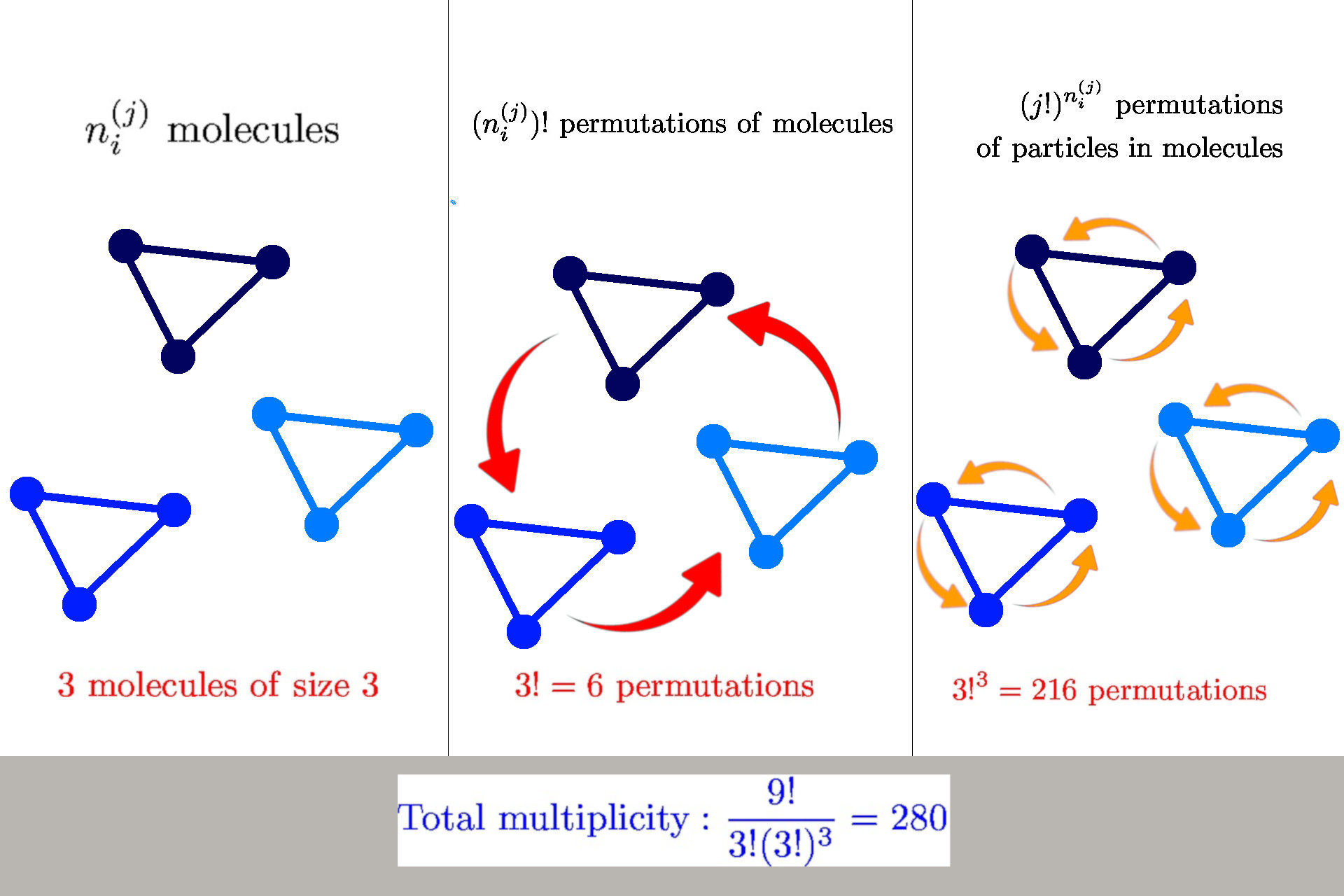
General formula: \(W(n_i^{(j)}) = \frac{n!}{\prod_{ij} n_i^{(j)}!  {\color{red} (j!)^{n_i^{(j)}}}}\)  

we have \(n_i^{(j)}\) molecules of size \(j\) in a state \(s_i^{(j)}\)

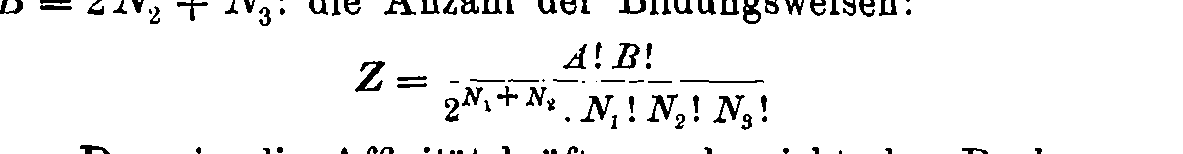
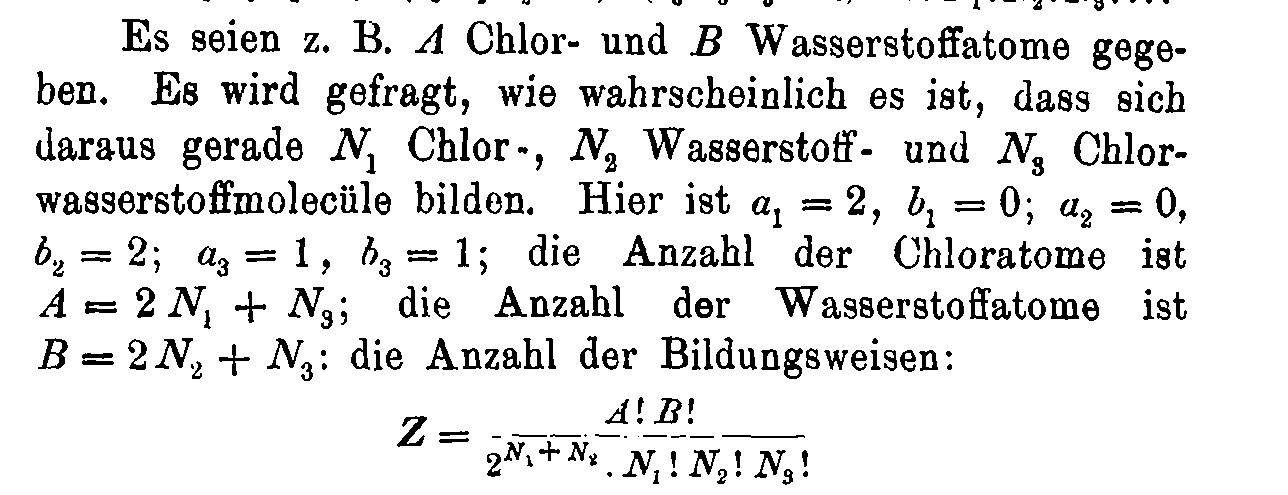
Boltzmann's 1884 paper

Entropy of structure-forming systems

$$ S =  \log W \approx n \log n - \sum_{ij} \left(n_i^{(j)} \log n_i^{(j)} - n_i^{(j)} + {\color{red} n_i^{(j)} \log j!}\right)$$

Introduce "probabilities" \(\wp_i^{(j)} = n_i^{(j)}/n\)

$$\mathcal{S} = S/n = - \sum_{ij} \wp_i^{(j)} (\log \wp_i^{(j)} {\color{red}- 1}) {\color{red}- \sum_{ij} \wp_i^{(j)}\log  \frac{j!}{n^{j-1}}}$$

Finite interaction range: concentration \(c = n/b\) 

$$\mathcal{S} = S/n = - \sum_{ij} \wp_i^{(j)} (\log \wp_i^{(j)} {\color{red}- 1}) {\color{red}- \sum_{ij} \wp_i^{(j)}\log  \frac{j!}{{\color{orange}c^{j-1}}}}$$

Equilibrium distribution:

$$\hat{\wp}_i^{(j)} = \frac{c^{j-1}}{j!} \exp(-\alpha j - \beta \epsilon_i^{(j)})$$

normalization by solving

\(\sum_{ij} j \wp_i^{(j)} = \sum_{ij} \frac{c^{j-1}}{(j-1)!} e^{-{\color{red} \alpha} j - \beta \epsilon_i^{(j)}} = 1\) for \({\color{red} \alpha}\)

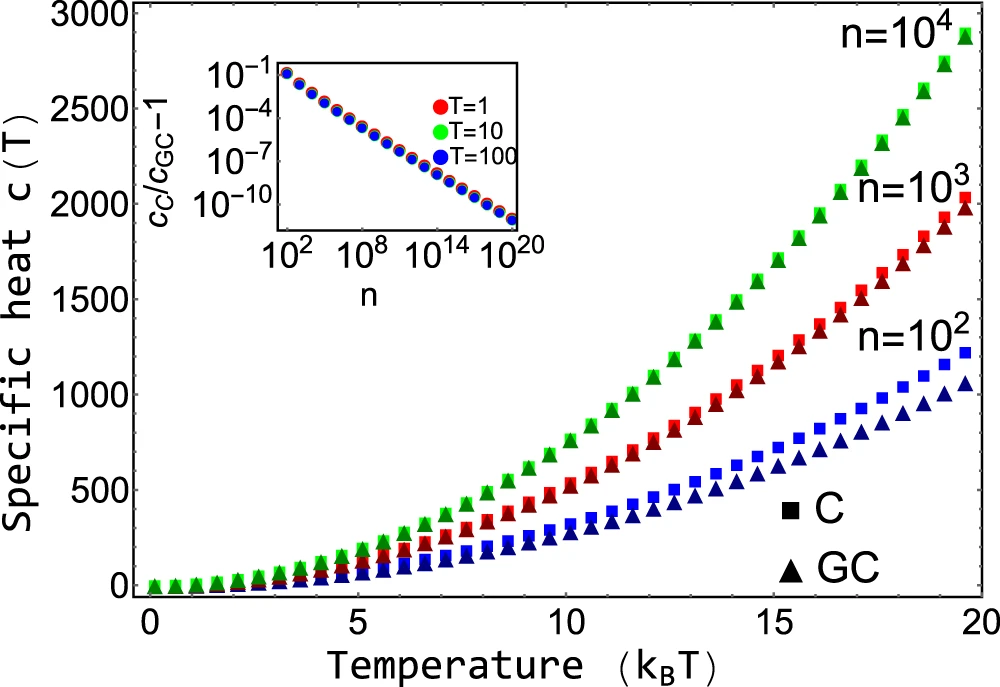
Comparison with Grand-canonical ensemble

Application: Self-assembly of Janus particles

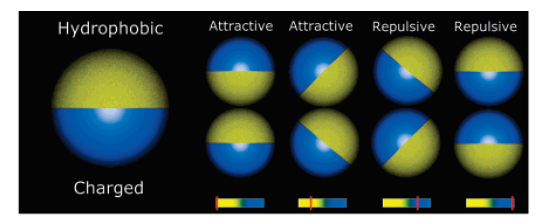
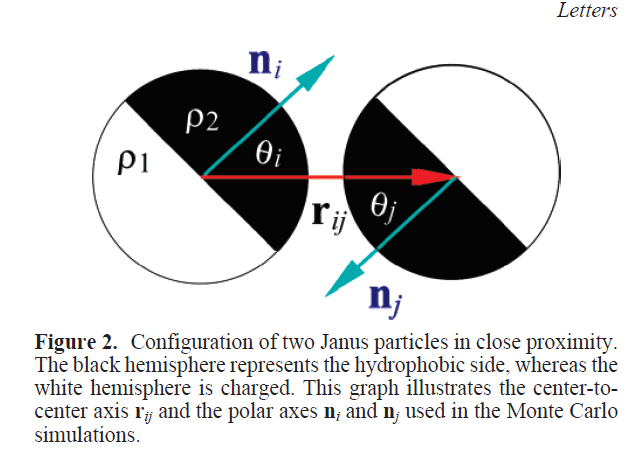
Kern-Frenkel model

Pair-wise potential: \(U^{KF}(r_{ij},n_i,n_j) = u(r_{ij}) \Omega(r_{ij},n_i,n_j) \)

Square-well interaction with hard sphere: 

$$ u(r_{ij}) = \left\{ \begin{array}{rl} \infty, & r_{ij} \leq \sigma \\  - \epsilon, & \sigma < r_{ij} < \sigma + \Delta \\ 0, & r_{ij} > \sigma + \Delta. \end{array} \right.$$

\(\Omega\) decribes orientation of particles:

Particle coverage \(\chi = \sin^2(\theta/2) = \frac{1-\cos{\theta}}{2}\)

Polymers: \(\chi = 0.3\)

Janus particles: \(\chi = 0.5\)

Crystalic structures: \(\chi = 0.6\) (stable lamellar crystals)

$$\Omega(r_{ij},n_i,n_j) = \left\{\begin{array}{rl} -1 & \mathrm{if} \  r_{ij} \cdot n_i > \cos(\theta) \ \mathrm{and} \ r_{ij} \cdot n_j > \cos(\theta)\\ 0 & \mathrm{otherwise} \end{array}  \right.$$

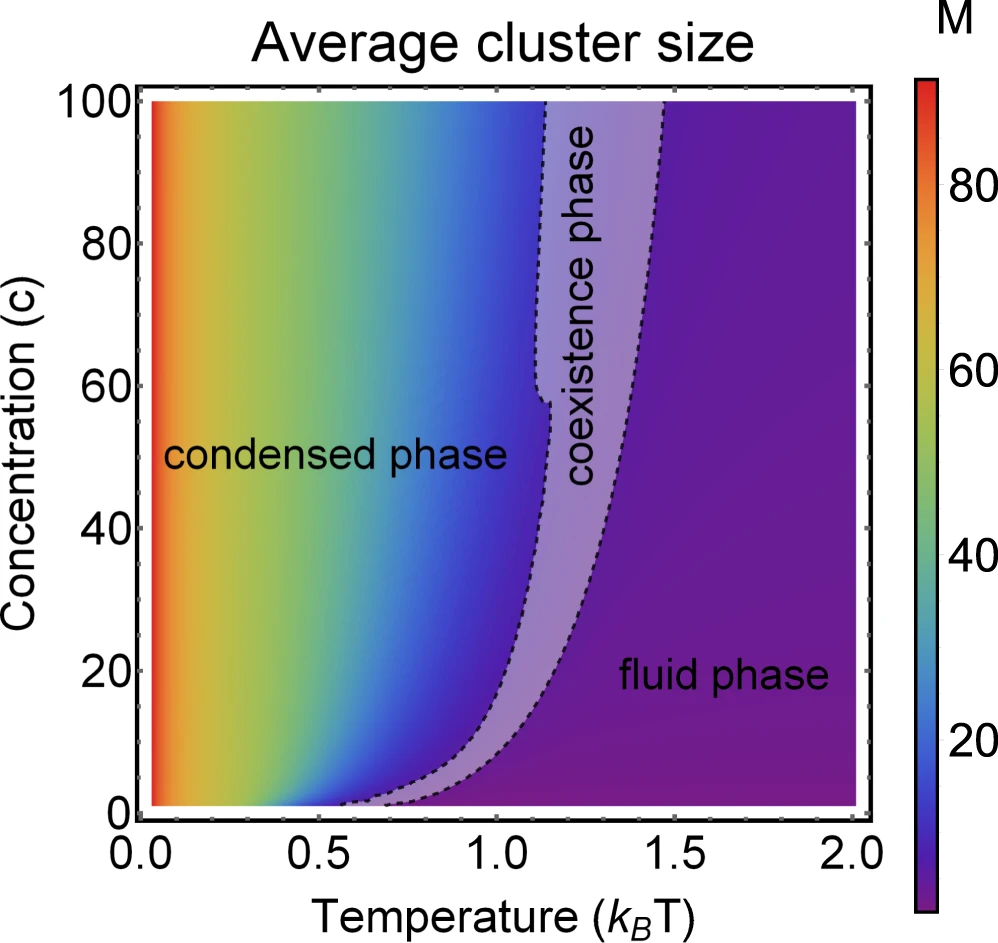
Phase diagram of Janus particles for average cluster size \(M\)

Application: Currie-Weiss model with molecules

(= fully connected Ising model with bound states)

$$ H(s_i) = - \frac{J}{n-1} \sum_{i \neq j, \ free} s_i s_j - h \sum_{j, \ free} s_j $$

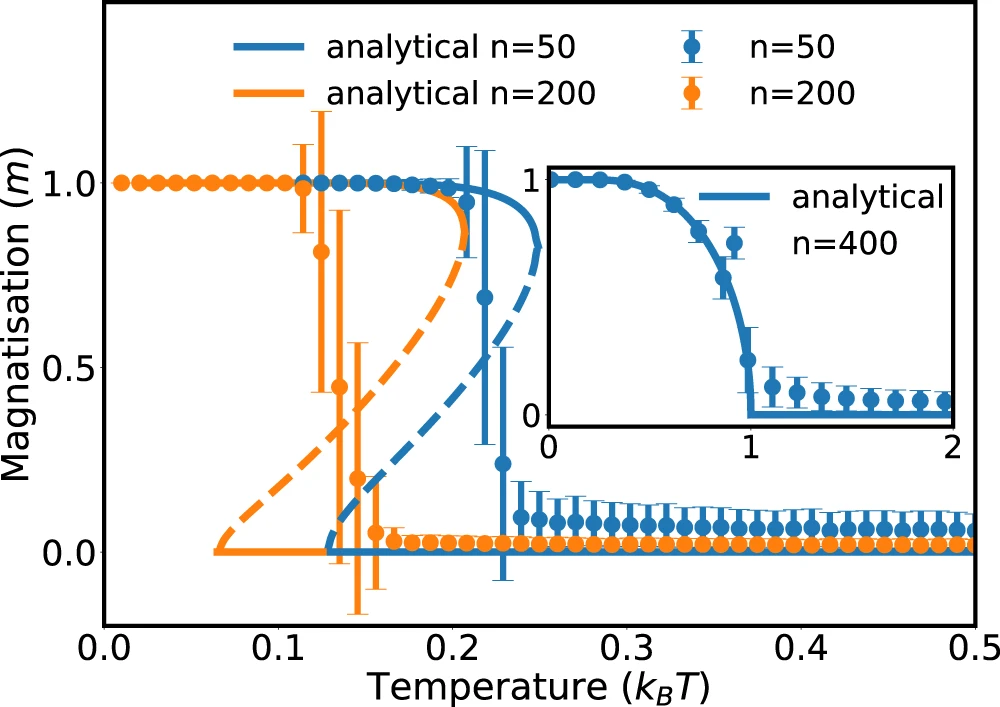
Application: Phase transitions in systems with several interactions

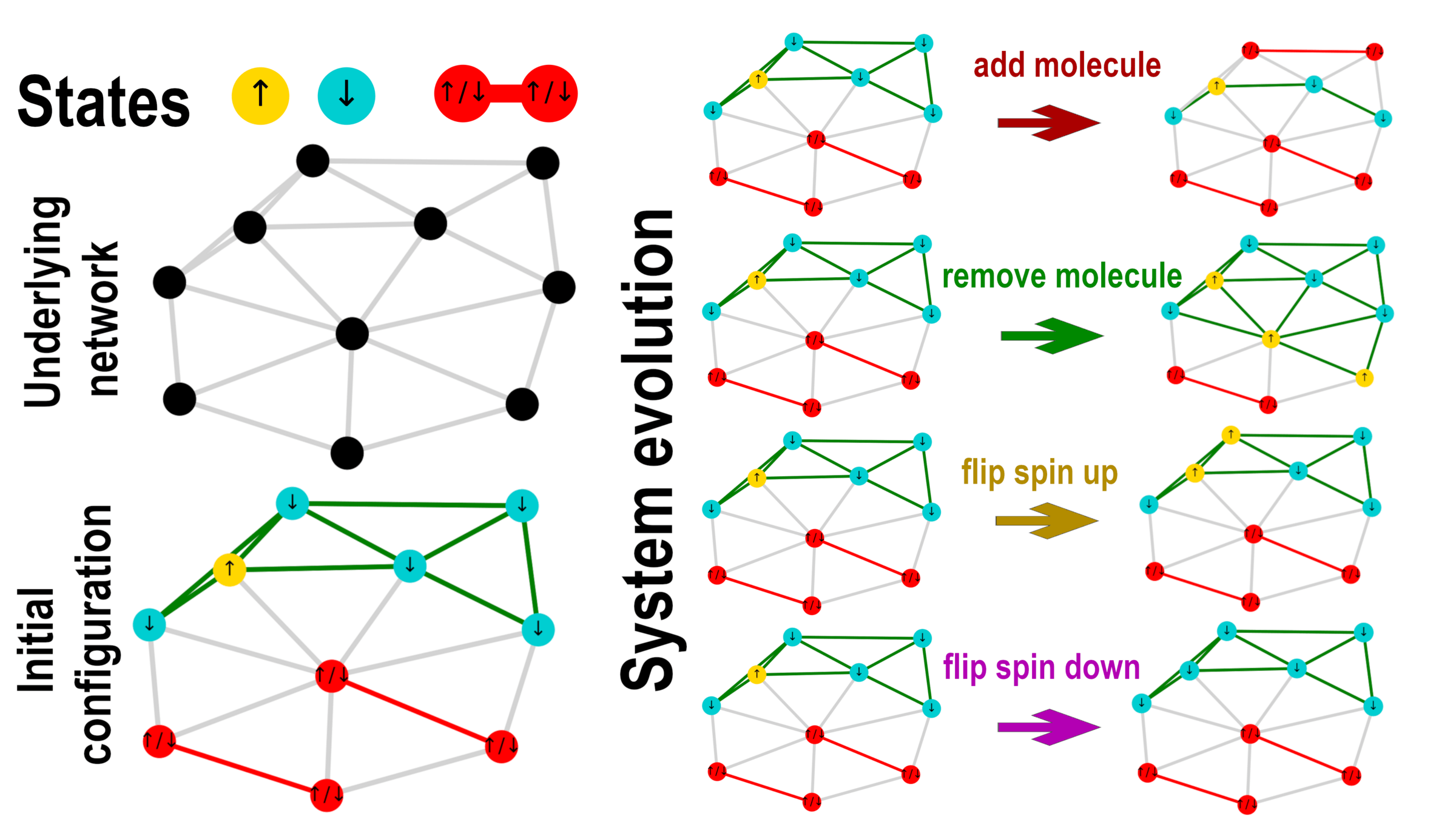
a fraction of particles \(q\) can form molecules

Phase diagram

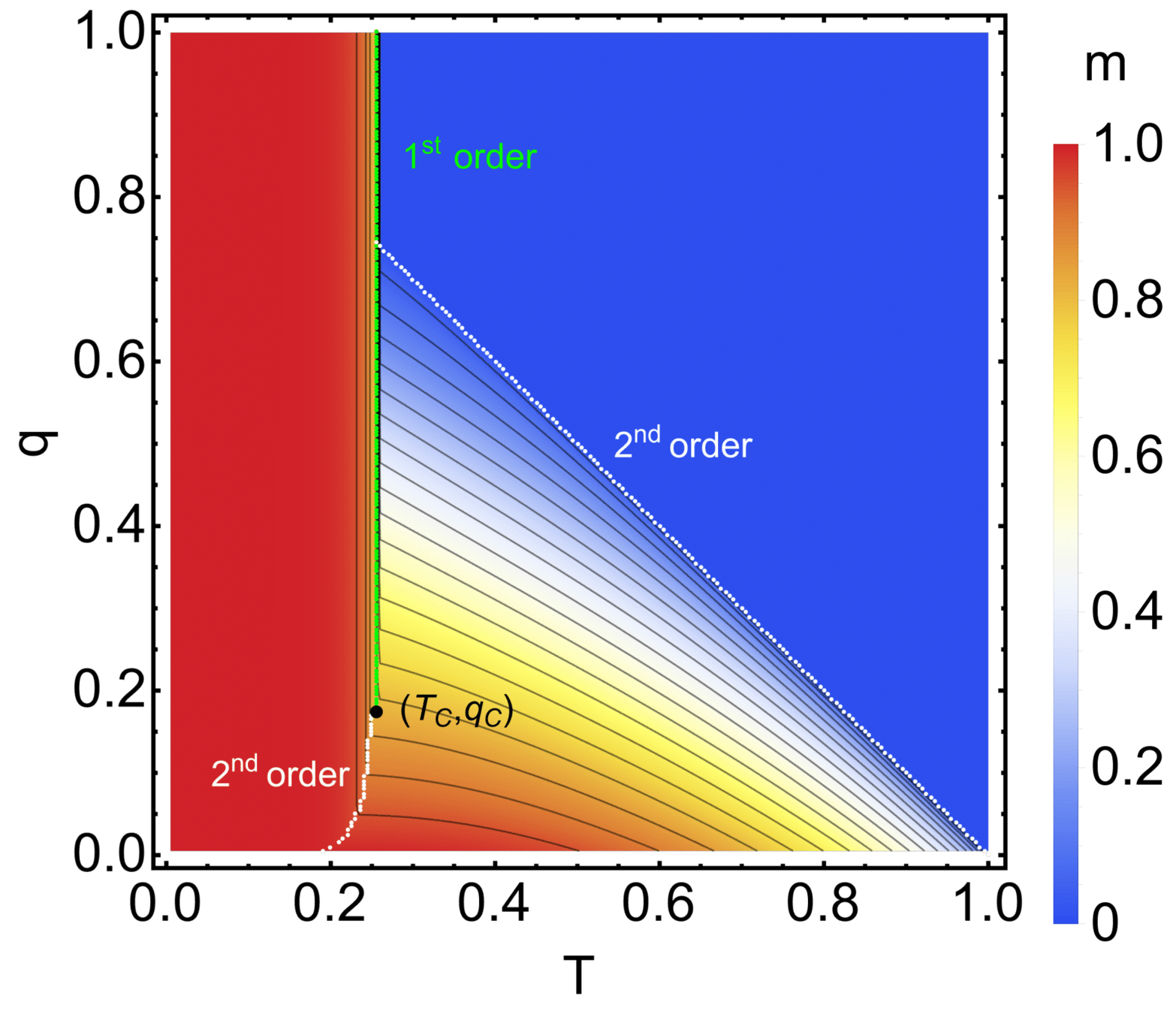
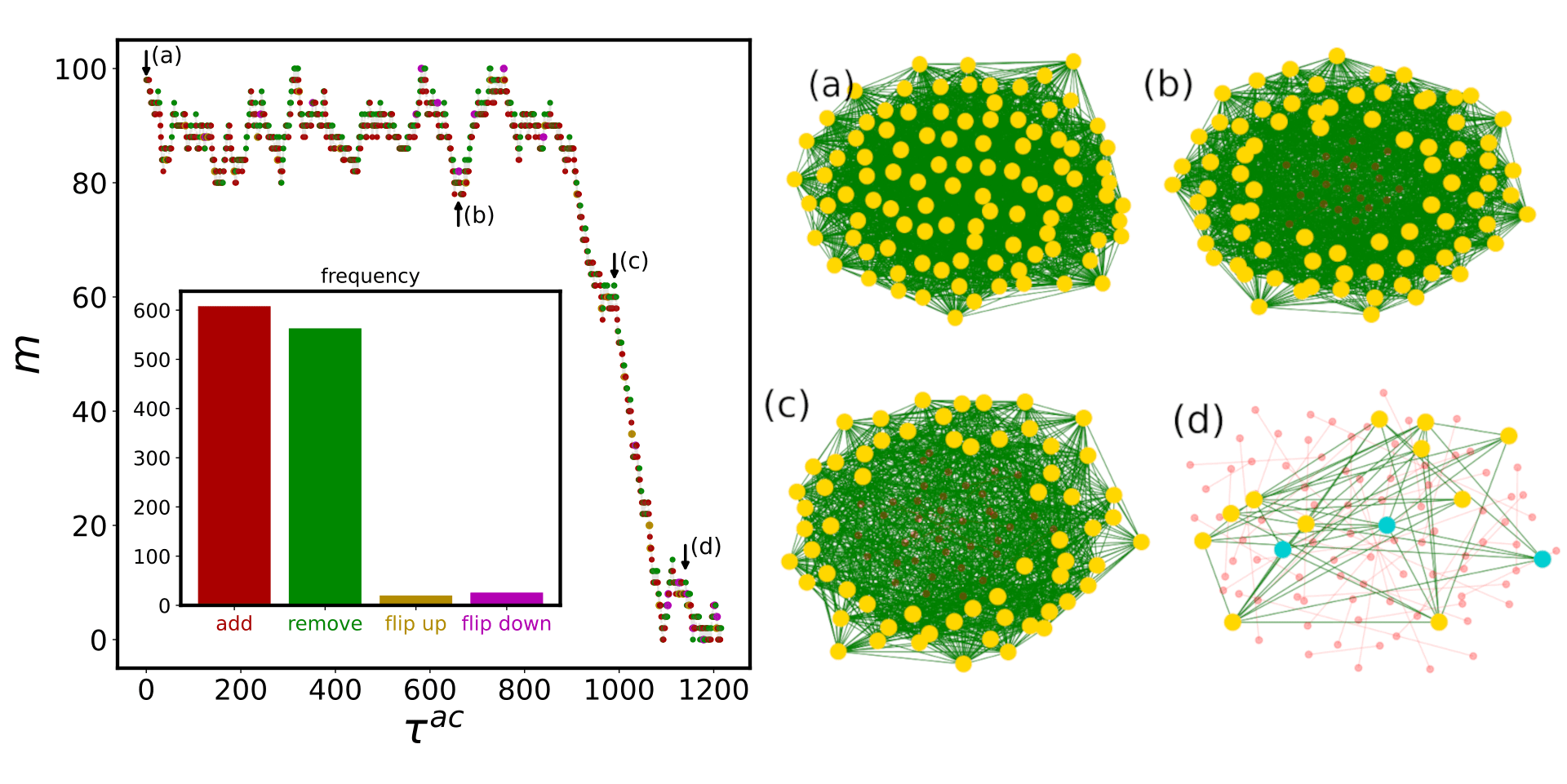
Microscopic origin

2. Spin glasses in opinion dynamics

Motivation

• Many opinion dynamics systems follow two basic concepts:

1. Homophily - people tend to be friends with peers with similar opinions
2.  Social balance - a friend of my friend is my friend, enemy of my friend is my enemy

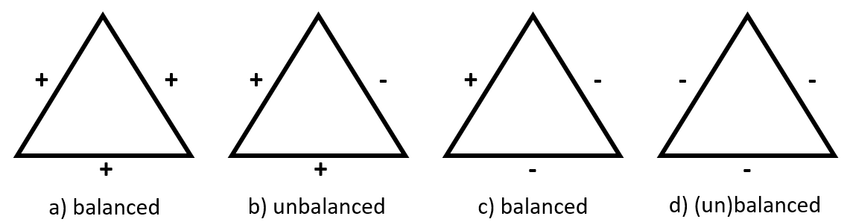
How are these two concepts related?

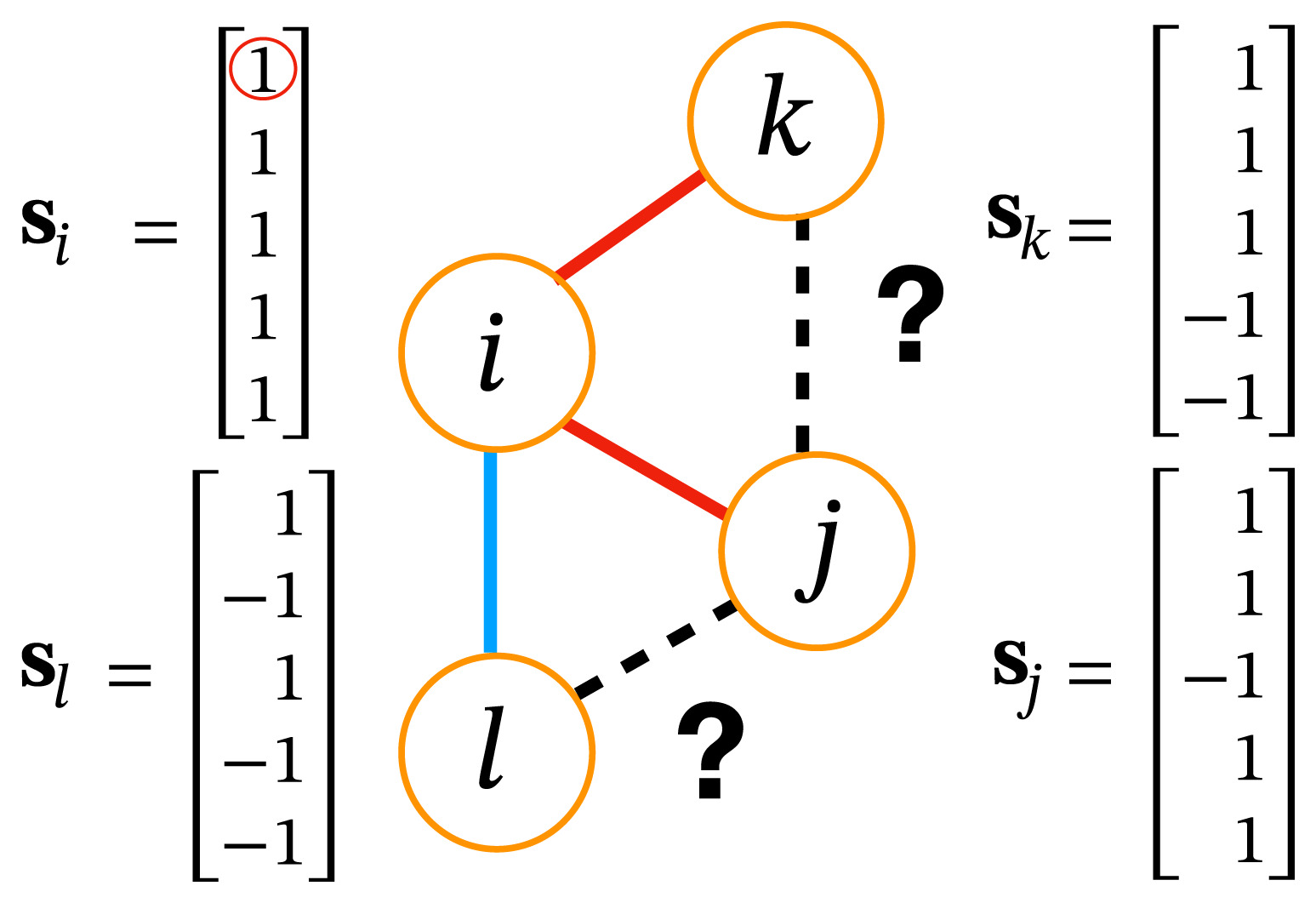
Friendship in large networks

In large networks, it is hard to know the relations among all our friends (a lot of information)

Local Hamiltonian approach

• We introduce a local Hamiltonian (=local stress) based on homophily and show how it is related to social balance
• Each individual has \(G\) binary opinions, \(s_i \in \{-1,1\}^G\)
• If two connected individuals have more common opinions than different opinions, they become friends and vice versa; \(J_{ij} = sign(s_i \cdot s_j)\)
• The local stress Hamiltonian is defined as $$H^{(i)} = -\frac{\alpha}{G} \sum_{j: J_{ij} =1} s_i \cdot s_j + \frac{1-\alpha}{G} \sum_{j: J_{ij} = -1} s_i \cdot s_j$$
• Parameter \(\alpha\) is the relative strength between friendship and enmity
• Individuals tend to minimize their local stress over time

• We define the following order parameters:
• Balance: \(f = \frac{n_{+}-n_{-}}{n_{+}+n_{-}}\) the relative difference of balanced and unbalanced triangles
• Average social stress: \(H = \sum_i H^{(i)}\)
• Similarity score: \(C = \frac{1}{NG} \sum_{i} \sum_{j: J_{ij}} \frac{s_i \cdot s_j}{N_i}\), where \(N_i\) is the number of friends of i

Order parameters

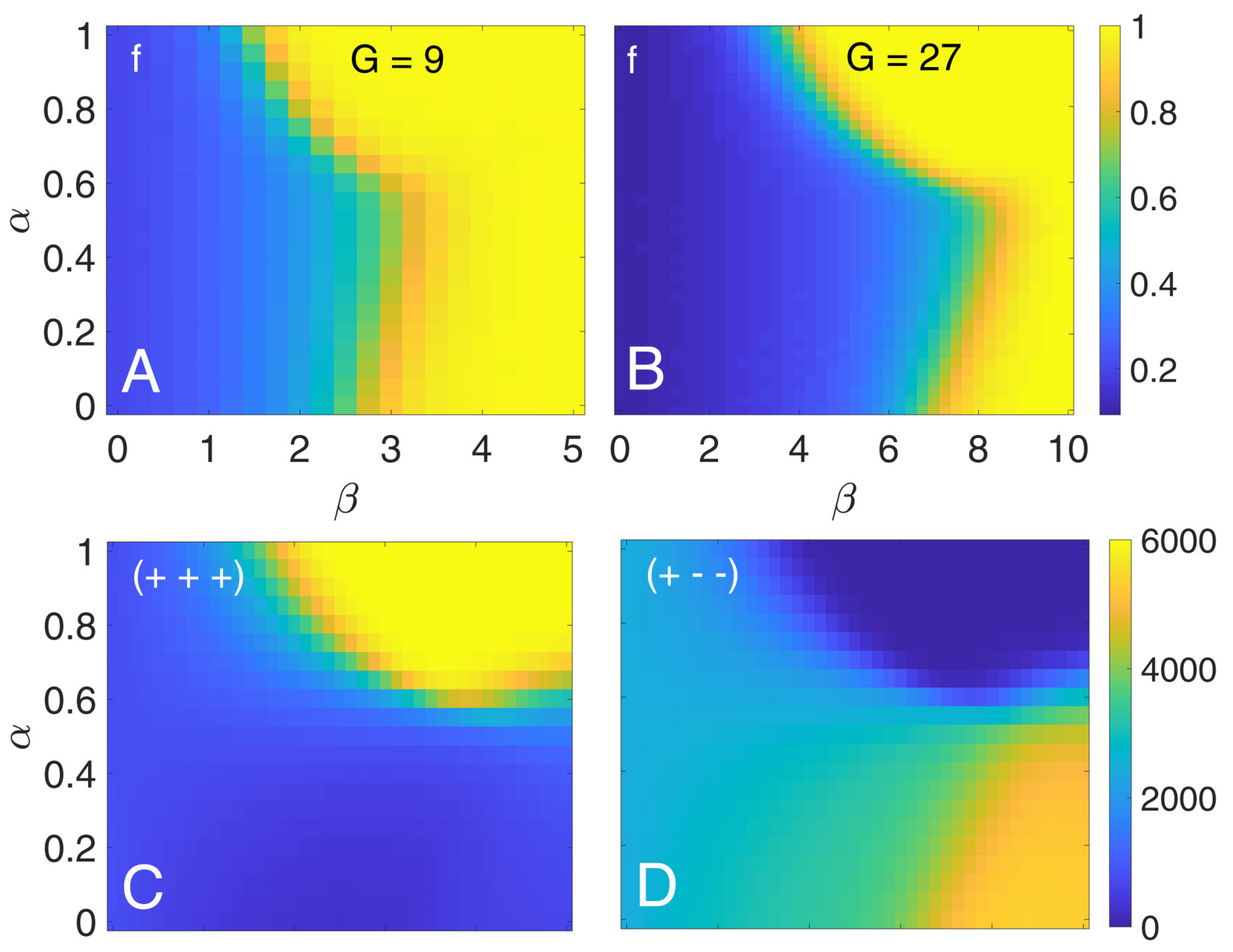
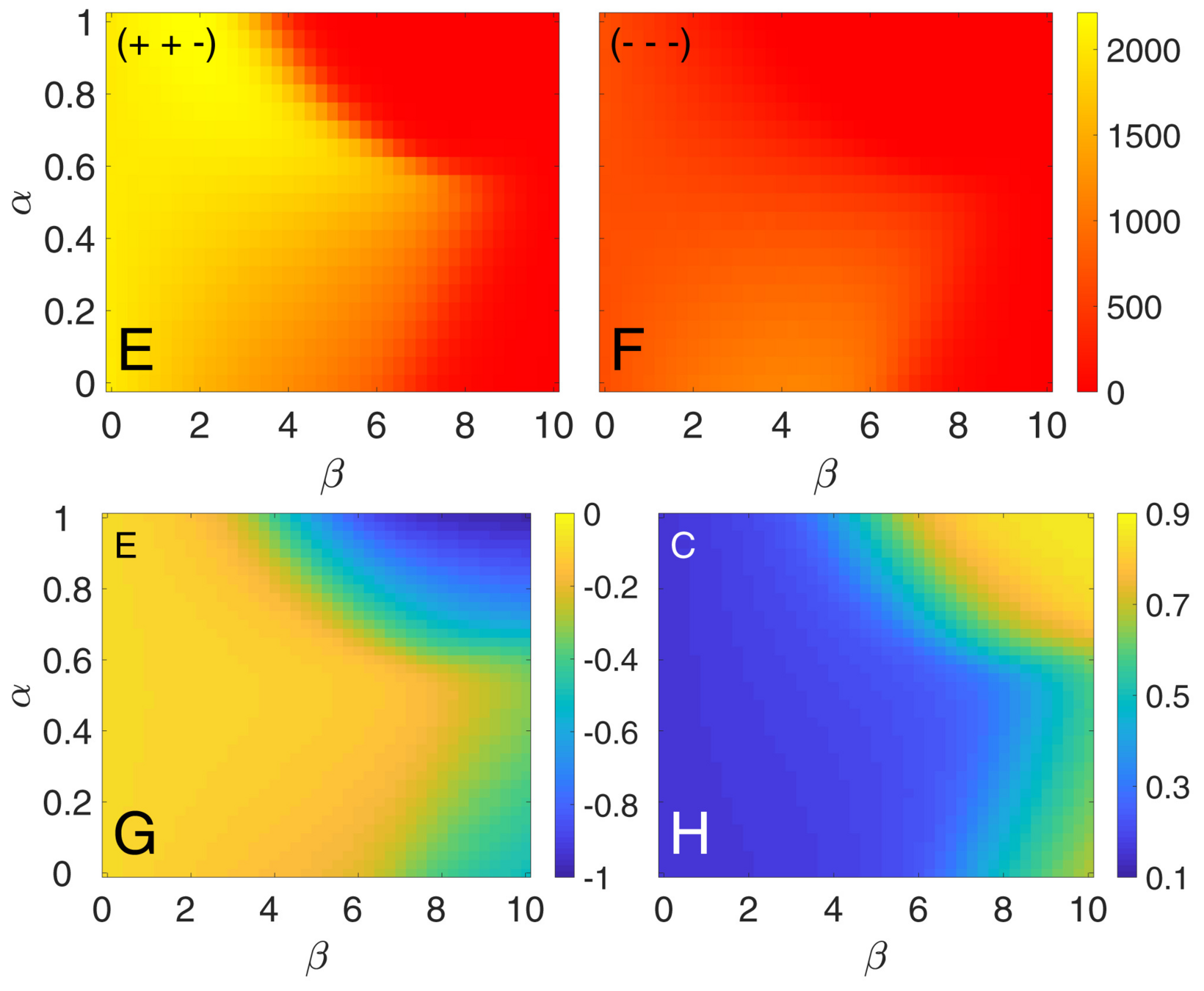
Phase diagrams

\(\beta\) represents "willingness to change",

the analog of inverse temperature

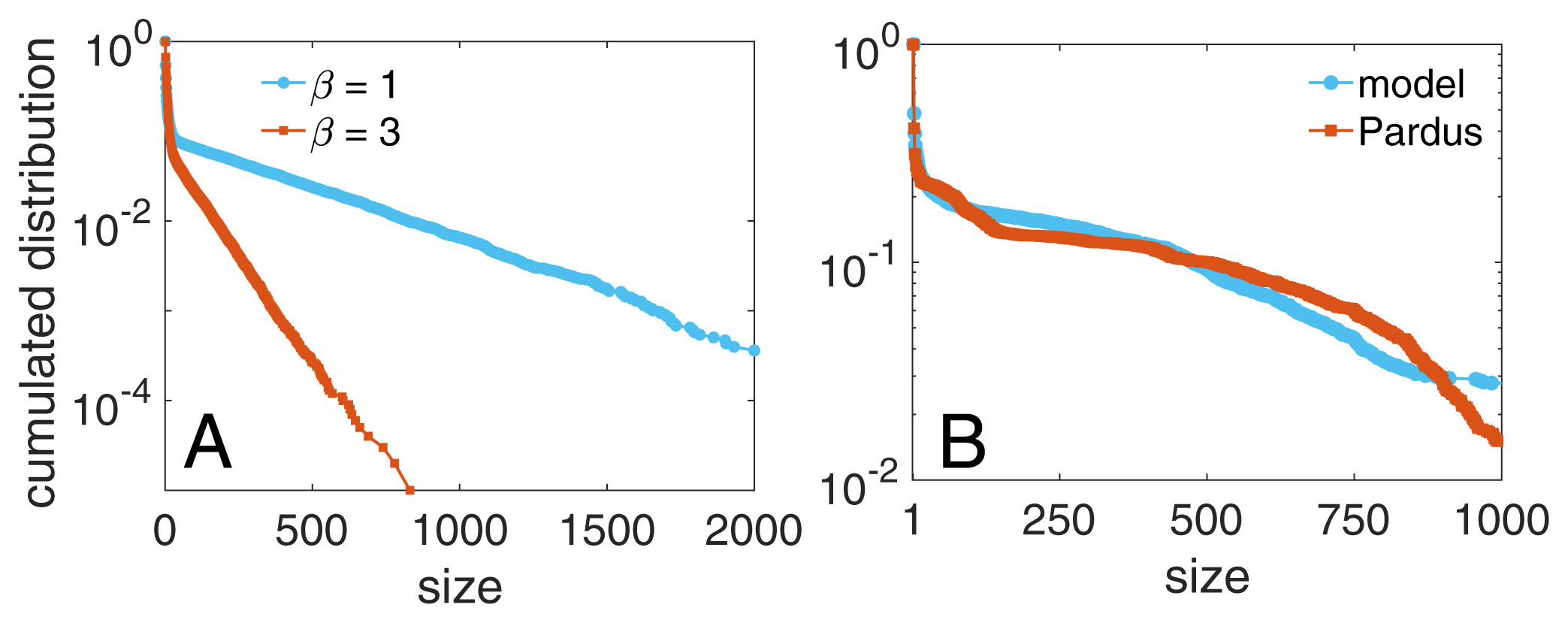
Group size distribution in Pardus

Pardus is an online multiplayer game where players have to interact with other peers 

3. Social group formation

Dora Brücke-Teleky award

Motivation

• Main motivation: application of soft-matter self-assembly and condensed-matter spin glasses in a new framework of social group formation based on homophily
• We use the equilibrium distribution from (1) and the local Hamiltonian from (2) to obtain the group-size distribution and the phase diagram
• Again, we compare it with the real data of Pardus

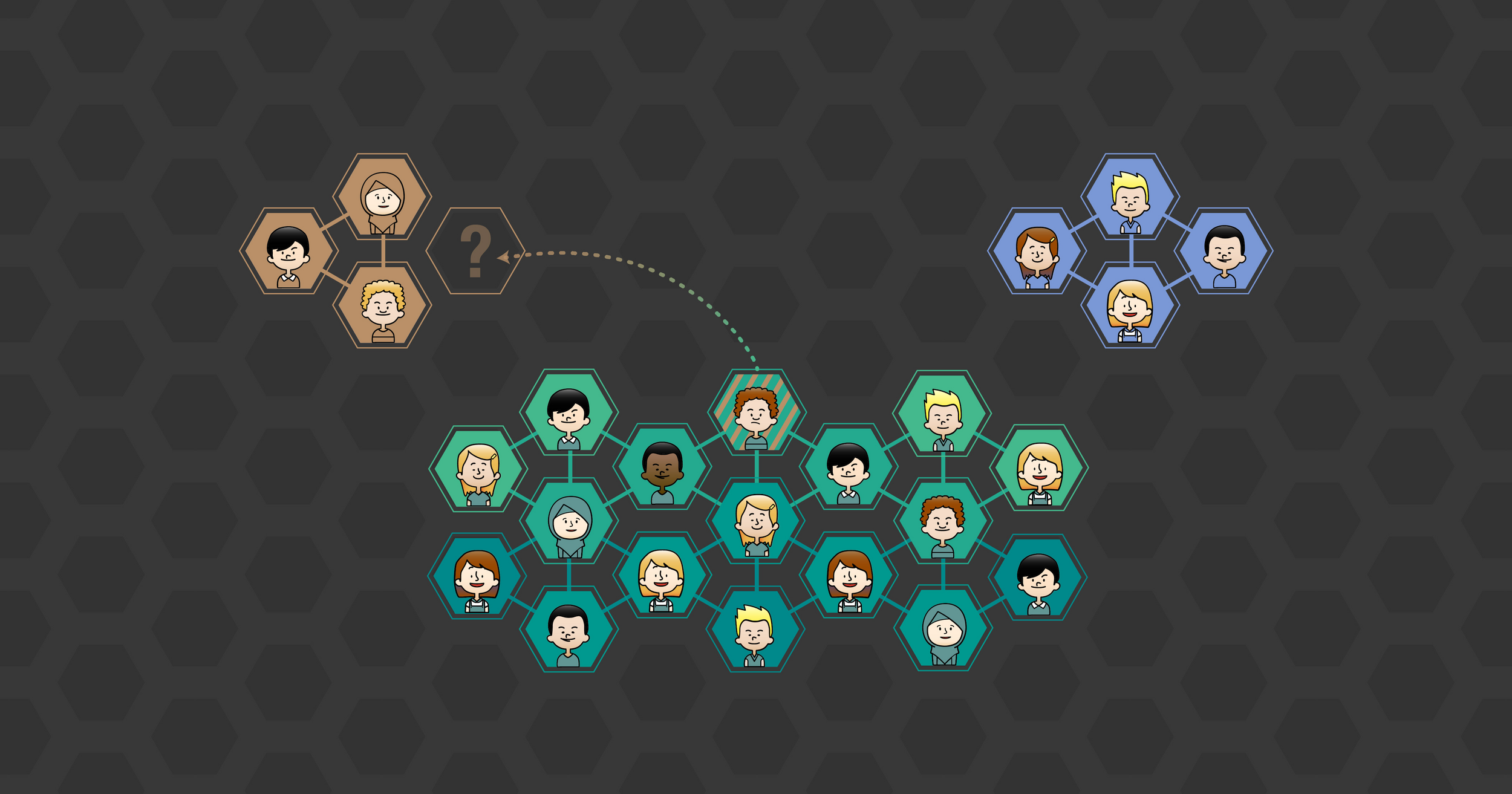
Group formation based on homophily

Hamiltonian of a group \(\mathcal{G}\)

\(H(\mathbf{s}_{i_1},\dots,\mathbf{s}_{i_k}) =  \underbrace{- \phi \, \frac{J}{2} \sum_{ij \in \mathcal{G}} A_{ij} \mathbf{s}_i \cdot \mathbf{s}_j}_{\textcolor{red}{intra-group \ social \ stress}}+ \underbrace{(1-\phi) \frac{J}{2} \sum_{i \in \mathcal{G}, j \notin \mathcal{G}} A_{ij} \mathbf{s}_{i} \cdot \mathbf{s}_j}_{\textcolor{blue}{inter-group \ social \ stress}} \\ \qquad \qquad \qquad \qquad - \underbrace{h \sum_{i \in \mathcal{G}} \mathbf{s}_i \cdot \mathbf{w}}_{external \ field}\)

Group formation based on opinion= self-assembly of spin glass

Group 1

Group 2

Approximations used in the model

1. Simulated annealing (configuration model)

- We do not know the full network, just a degree distribution. The probability of observing a link between \(i\) and \(j\) is proportional to the degree i.e., \(A_{ij} \propto k_i k_j\)

2. Mean-field approximation

- We replace the original Hamiltonian by the mean-field approximation, where \(m^{(k)} = \sum_{i \in group \ of \ size \ k} s_i\) is the average opinion vector of a group of size \(k\)

These two approximations lead to the set of self-consistency equations:

$$m^{(k)} = k \sum_{q^{(k)} q^{(k,l)}} P(q^{(k)}) P(q^{(k,l)}) \tanh(\beta H^{(k)}(m^{(l)},q^{(k)},q^{(k,l)})) $$

where \(q^{(k)}\) is the intra-group degree, \(q^{(k,l)}\) is the inter-group degree and \(P\) is the degree distribution

Results for zero inter-group degree

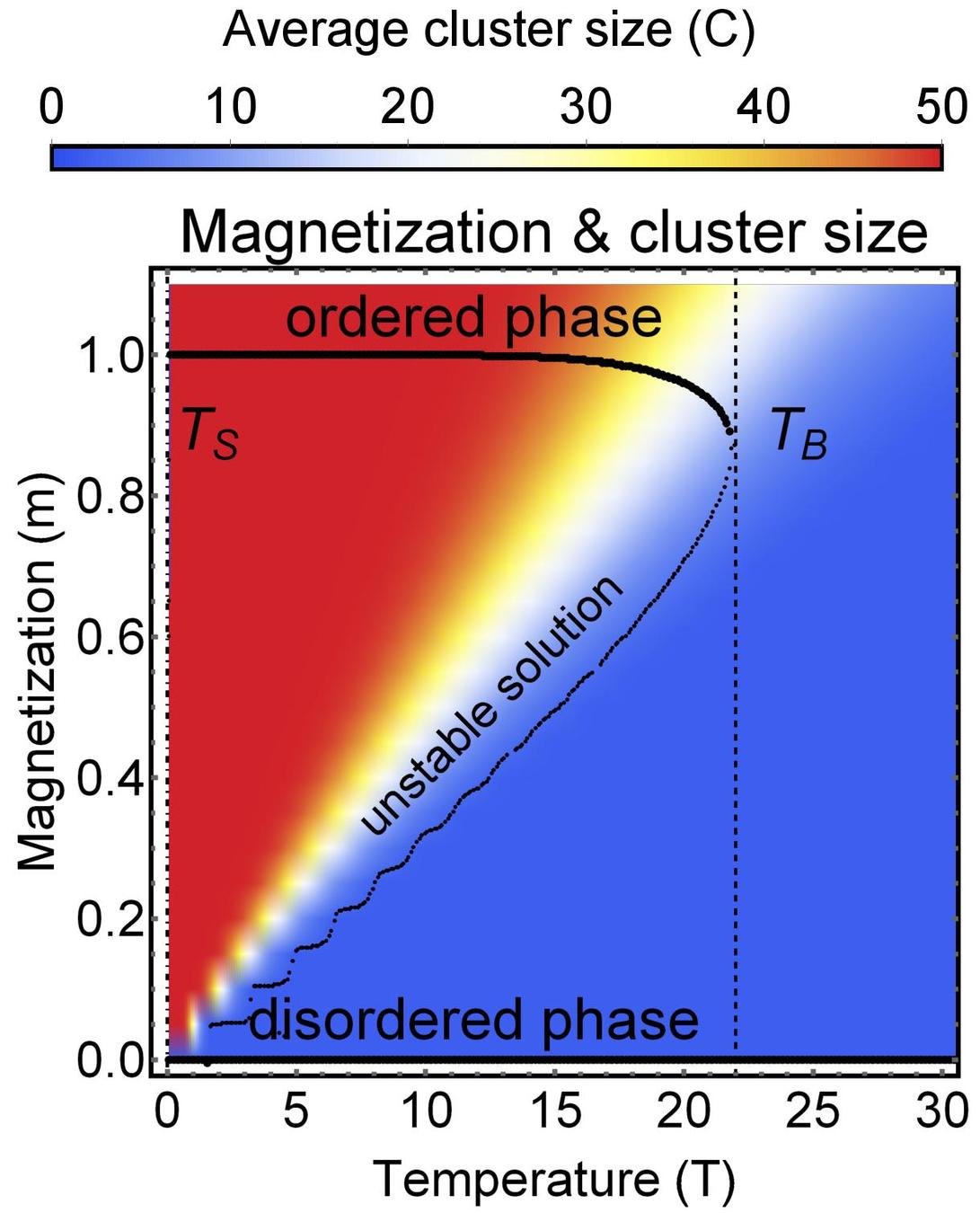
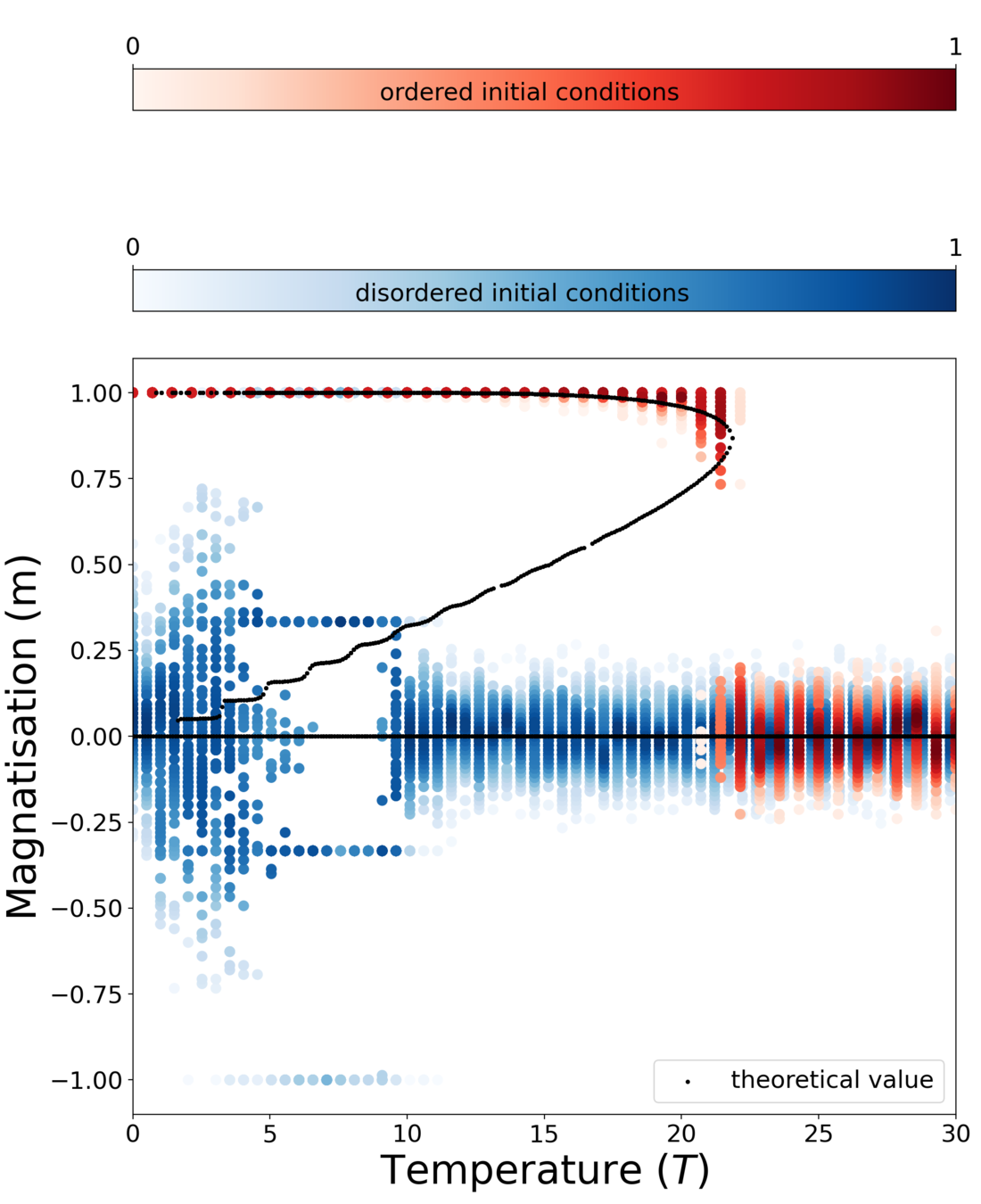
Theory

MC simulation

Dependence on external field

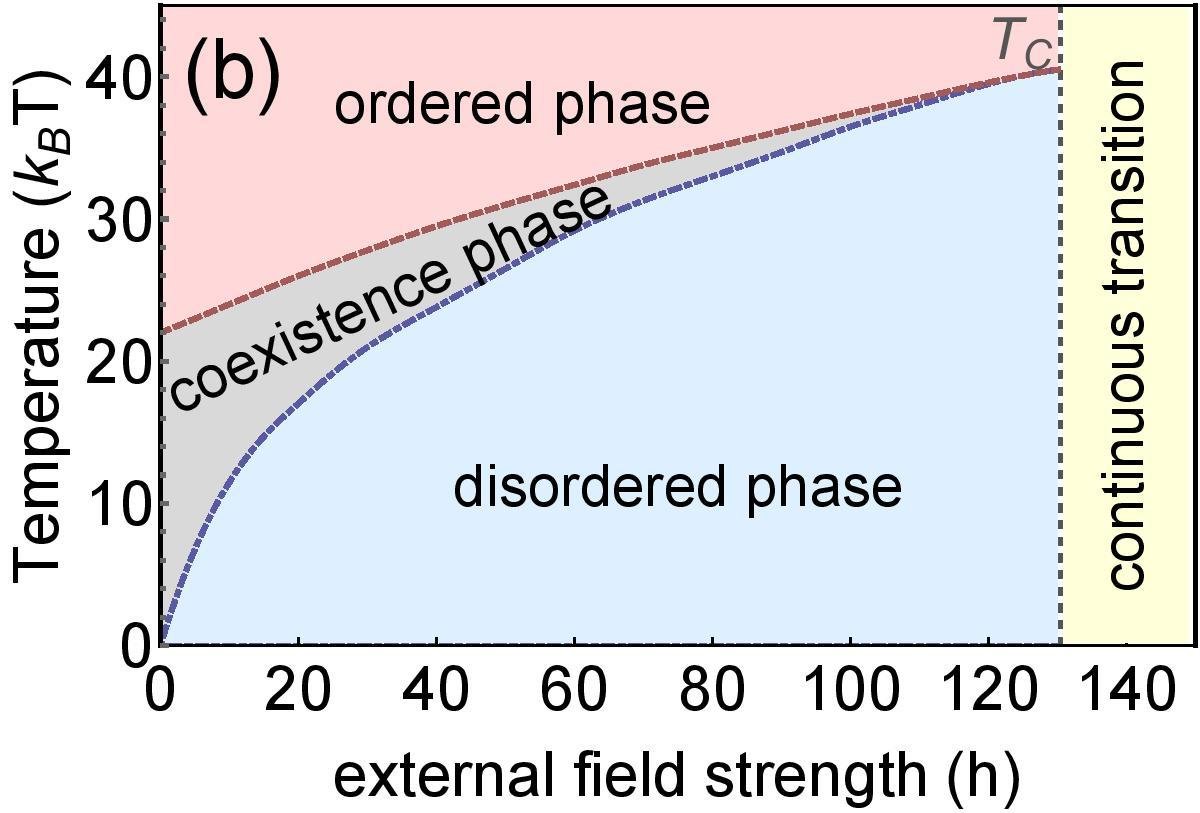
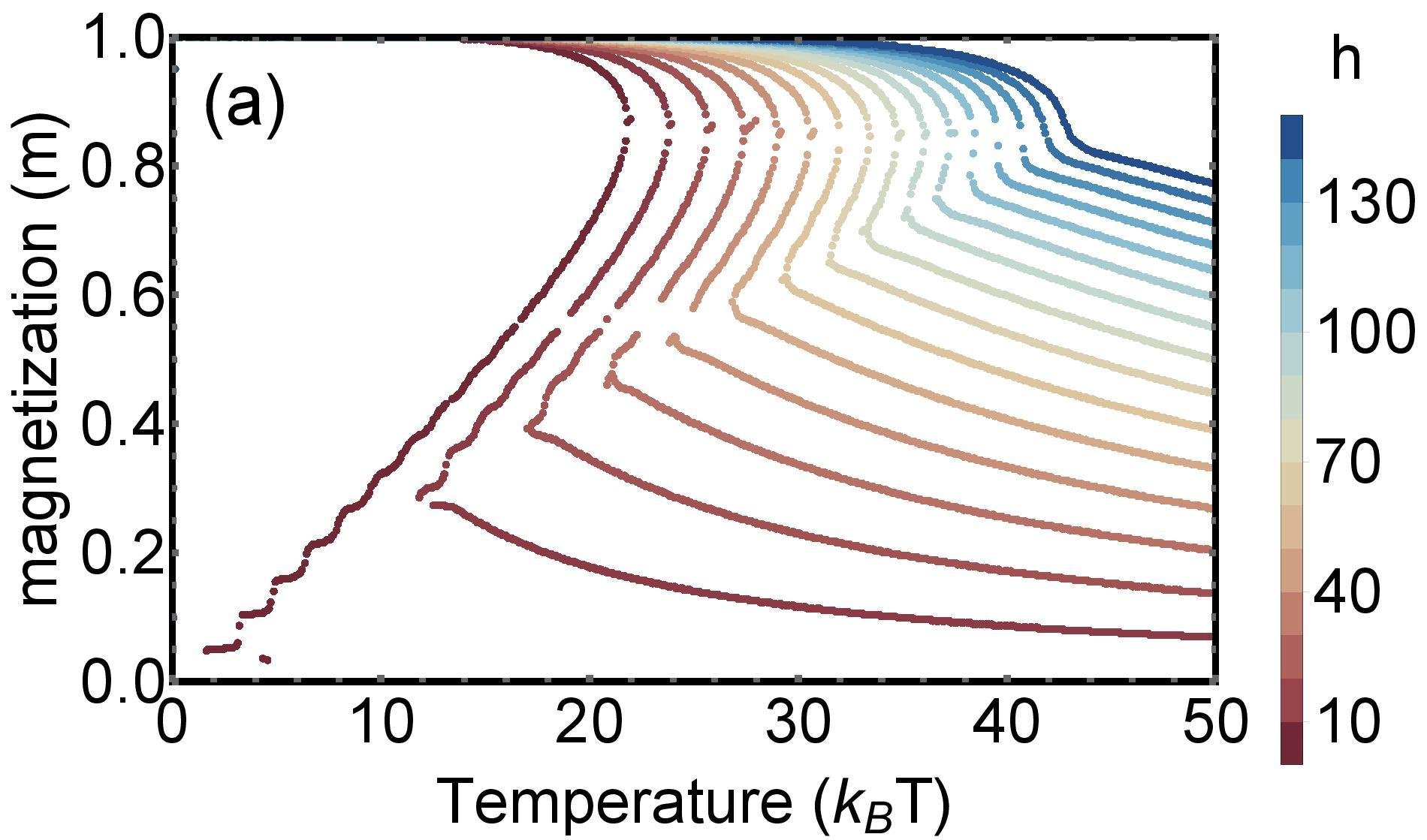
Application: PARDUS multiplayer online game

Summary and future research

• Based on physical models of self-assembly and spin glasses, we created a homophily-based social group formation model that requires only a few parameters, as average friendship degree
• The model has some limitations indeed: 
  1. Lack of higher-order structures in the network (e.g., triangles)
  2. Lack of enmity relations within groups 
  3. Opinions are considered to be independent (no belief system)
  4. Real social networks are typically multilayer (family x work x leisure)
  5. Influence of different opinions on different types of links 
• All the limitations are suggestions for future work