Applications of fractional diffusion in option pricing

Jan Korbel

CCS Satelite on Econophysics, 27th October, Lyon

slides available at: slides.com/jankorbel

Option pricing

• First option pricing model (Black and Scholes 1973) 
  • based on ordinary Brownian motion
  • Nobel prize in economics (Scholes, Merton) - 1997
• ​In financial crises or in complex markets, the model cannot catch
  realistic market dynamics
  • large drops, sudden shocks, memory effects
• Finite moment log-stable model (Carr and Wu 2003)
  • based on Lévy-stable fractional diffusion
  • enables large drops
• We generalize the models by using space-time fractional diffusion equation

Space-time fractional diffusion 

The STFD equation is defined as

$$ \left({}^*_0 \mathcal{D}^\gamma_t - \mu \ {}^\theta \mathcal{D}_x^{\alpha}\right) g(x,t) = 0$$

Caputo derivative: \( {}^*_{t_0} \mathcal{D}^\gamma_t f(t) = \frac{1}{\Gamma(\lceil \gamma \rceil - \gamma)} \int_{t_0}^t \mathrm{d} \tau \frac{f^{\lceil \gamma \rceil}(\tau)}{(t-\tau)^{\gamma + 1 - \lceil \gamma \rceil}}\)

Riesz-Feller derivative: \(\mathcal{F}[{}^{\theta} \mathcal{D}^\alpha_x f(x)](k) = -|k|^\alpha e^{i \, \mathrm{sign}(k) \theta \pi/2} \mathcal{F}[f(x)](k) \)

Solution can be defined in terms of Mellin-Barnes transform

$$g_{\alpha,\theta,\gamma}(x,t) = \frac{1}{2 \pi i} \frac{1}{\alpha x} \int_{c-i \infty}^{c+i \infty} \frac{\Gamma(\frac{y}{\alpha}) \Gamma(1-\frac{y}{\alpha})\Gamma(1-y)}{\Gamma(1-\frac{\gamma}{\alpha} y)\Gamma(\frac{\alpha-\theta}{2 \alpha} y) \Gamma(1- \frac{\alpha-\theta}{2 \alpha} y)} \left(\frac{x}{-\mu t}\right)^y \mathrm{d} y$$

[1] Physica A 449 (2016) 200-214

Space-time fractional diffusion 

• \(\gamma=1, \alpha=2\) - ordinary Gaussian diffusion

• \(\gamma=1, \alpha<2\) - Lévy-stable diffusion

• \(\gamma \neq 1, \alpha=2\) - diffusion with memory

• \(\gamma \neq 1, \alpha<2\) - space-time fractional diffusion

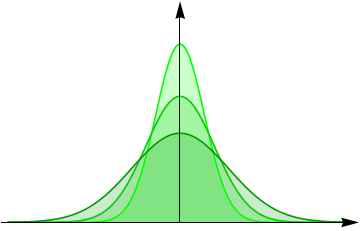
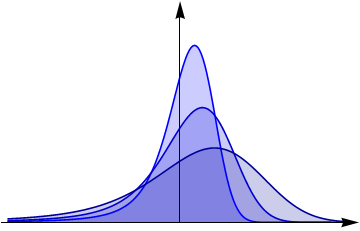
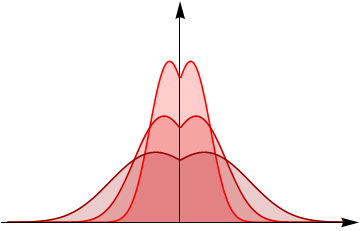
[6] Mathematics 7 (9) (2019) 796

Space-time fractional option pricing

Price of European call option: $$C(S,K,\tau) = \int_{-\infty}^\infty \max\{S e^{(r+\mu) \tau + x}-K,0\} g_{\alpha,\theta,\gamma}(x,\tau) \mathrm{d} x$$

Interpretation of parameters:

• \(\theta = \max\{-\alpha, \alpha-2\}\) 
  • maximally asymmetric distribution
  • power-law probability of drops (negative Lévy tail)
  •  Gaussian probability of rises (positive exponential tail
• \(\alpha < 2\) - risk redistribution to large drops
• \(\gamma \) - risk redistribution in time
  • \(\gamma < 1\) shorter contracts are more risky
  • \(\gamma > 1\) longer contracts are more risky

[1] Physica A 449 (2016) 200-214; [3] Fractal Fract. 2 (1) (2018) 15

Double-series representation

By using residue summation in \(\mathbb{C}^2\) it is possible to express the price in terms of rapidly-convergent double series ( \(\mathcal{L} = \log \frac{S}{K} + r \tau\) ) 

$$C(S,K,\tau) = \frac{K e^{-r \tau}}{\alpha}  \sum_{n=0}^\infty \sum_{m=1}^\infty \frac{1}{n! \Gamma\left(1 + \frac{m-n}{\alpha}\right)}(\mathcal{L}+\mu \tau)^{n}(-\mu \tau)^{\frac{m-n}{2}}$$

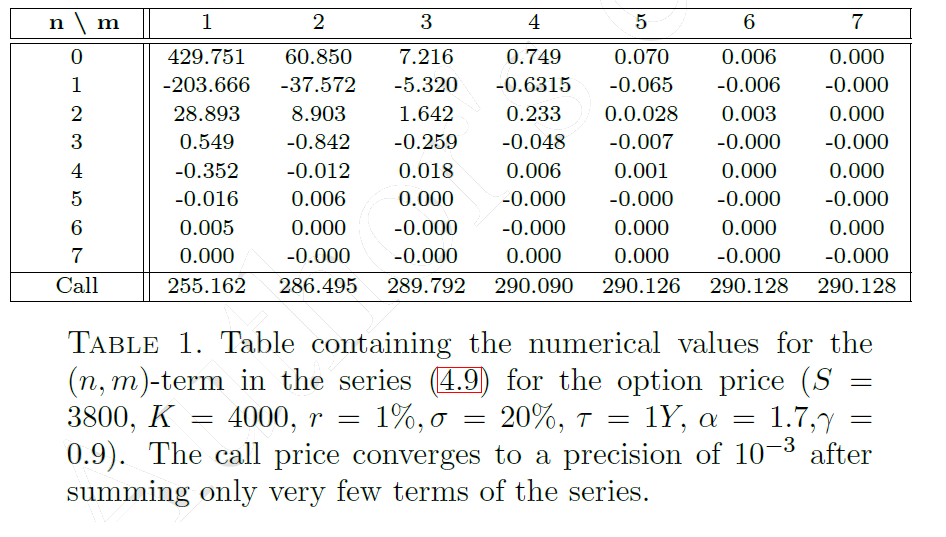
[4] Fract. Calc. Appl. Anal. 21 (4) (2018) 981-1004

Subordinator representation

\(g_{\alpha,\theta,\gamma}(x,t)\) can be represented as a subordinated process

$$g_{\alpha,\theta,\gamma}(x,t) = \int_0^\infty \mathrm{d} l K_\gamma(t,l) L_{\alpha}^\theta(l,x)$$

• \(L_{\alpha}^\theta(l,x)\) - Lévy-stable distribution with scaling parameter \(l\) 
• \(K_\gamma(t,l\) - subordinator (smearing kernel)
  • \(K_\gamma(t,l) =  \frac{t}{l^{1+1/\gamma} \gamma}  L_\gamma^{\gamma}\left(\frac{t}{l^{1/\gamma}}\right)\)
• We compare with other subordinated models
  • Variance gamma \(K_\lambda(t,l) =  \lambda  e^{\lambda  (-t/l)}\)
  • Negative inverse-gamma \(K_{\alpha,\beta}(t,l) = \frac{e^{-\frac{\beta }{t/l}} \left(\frac{\beta }{t/l}\right)^{\alpha }}{t/l \Gamma (\alpha )}\)

[1] Physica A 449 (2016) 200-214; [8] Risks 8 (4) (2020) 124

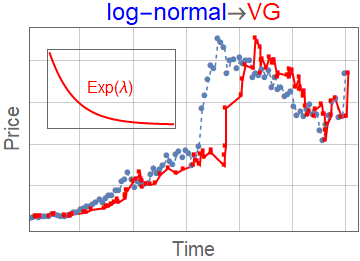
Subordinator representation

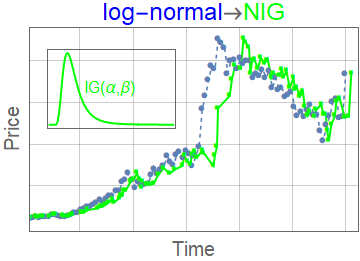
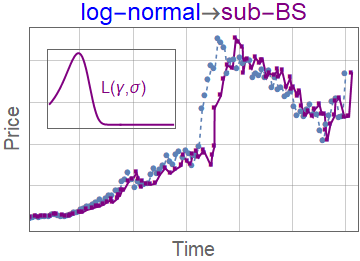
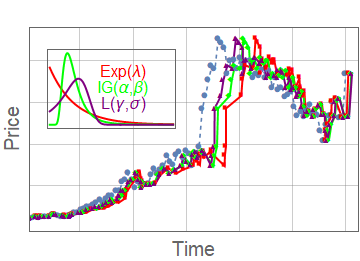
Other results

• Space-time fractional option pricing with varying order of fractional derivatives
  • [3] FCAA 19 (6) (2016) 1414-1433

• Pricing of more exotic types of options (American, digital,...) under the space-time fractional diffusion model and formulas for the risk sensitives  ("the Greeks" - Gamma, Delta, Rho,...)
  • [5] Risks 7 (2) (2019) 36; 10.3390/risks7020036
  • [6] Mathematics 7 (9) (2019) 796; 10.3390/math7090796

• ​Option pricing with more complicated fractional diffusion equation based on Hilfer-Prabhakar fractional derivative​
  • [7] Fract. Calc. Appl. Anal. 23 (4) (2020) 996-1012

Thank you!

Keywords: option pricing, Black–Scholes model, fractional calculus, fractional diffusion, long-term memory, Lévy stable processes, jump processes, fractional Brownian motion, subordinated models, Bergomi model, rough volatility models