Stochastic thermodynamics in uncertain environments

Jan Korbel & David Wolpert

CSH Workshop "Stochastic thermodynamics of complex systems" 30th September 2021

Slides available at: https://slides.com/jankorbel

Motivation

System

heat bath

prepared at

 \(T_1\)

Typical experiment

heat bath

prepared at

 \(T_2\)

work reservoir

Typical experiment

\(T\)

\(X\)

\(P(T)\)

\(X\)

3rd trial

\(T_3\)

\(X_3\)

...

In reality

Measure a quantity \(X\) and the temperature \(T\)

Temperature is measured with limited precision

In many experiments

• We do not know exact value of
  • amount of heat baths
  • temperatures
  • chemical potentials
  • energy spectrum
  • control protocol
  • transition rates
  • initial distribution

In real experiments, there is always some uncertainty about the system and its environment

Related approaches

Stochastic thermodynamics

Stochastic thermodynamics

1.) Consider linear Markov (= memoryless) with distribution \(p_i(t)\).

Its evolution is described by the master equation

$$ \dot{p}_t(x) = \sum_{x'} [K_{xx'} p_{t}(x') - K_{x'x} p_t(x) ]$$

\(K_{xx'}\) is transition rate. 

2.) First law of thermodynamics - internal energy \( U = \sum_x p(x) u(x) \) then First law of thermodyanmics is

\(\dot{U} = \sum_x \dot{p}_t(x) u_t(x) + \sum_x p_t(x)  \dot{u}_t(x) = \dot{Q} + \dot{W}\)

\(\dot{Q}\) - heat rate

\(\dot{W}\) - work rate

Stochastic thermodynamics

3.) Entropy of the system - Shannon entropy  \(S = - \sum_x p_x \log p_x\). Equilibrium distribution is obtained by maximization of \(S\) under the constraint of average energy 

$$ \pi(x) = \frac{1}{Z} \exp(- \beta u(x)) \quad \mathrm{where} \ \beta=\frac{1}{k_B T}, Z = \sum_x \exp(-\beta u(x))$$

4.) Detailed balance - stationary state (\(\dot{p}_t(x) = 0\) ) coincides with the equilibrium state \(\pi(x)\). We obtain

$$\frac{K_{xx'}}{K_{x'x}} = \frac{\pi(x)}{\pi(x')} = e^{\beta(u(x') - u(x))}$$

Note: Transition rate satisfying LDB

a.) General form of transition matrix satisfying detailed balance

      Equilibrium distribution \(\pi\):        \( K \pi = 0\)

      Define:                                            \(\Pi := diag(\pi)\)

      DB condition:                              \(K \Pi = (K \Pi)^T \)

      Decomposition:                             \( K = R \Pi^{-1} \), \(R\) - symmetric

      Normalization:                               \( K = R \Pi^{-1} - diag (R \Pi^{-1} \cdot \mathbf{1}) \)

 b.) General form of transition matrix satisfying LDB

          $$K = \sum_{\nu=1}^N \left[ R^\nu (\Pi^\nu(\beta_\nu,\mu_\nu))^{-1} - diag (R^\nu \Pi^\nu(\beta_\nu,\mu_\nu))^{-1} \cdot \mathbf{1}\right]$$

Stochastic thermodynamics

5.) Second law of thermodynamics:

$$\dot{S} = - \sum_x \dot{p}_x \log p_x = \frac{1}{2} \sum_{xx'} \left[K_{xx'} p_t(x') - K_{x'x} p_t(x)\right] \log \frac{p_t(x')}{p_t(x)}$$

$$ =\underbrace{\frac{1}{2} \sum_{xx'} \left[K_{xx'} p_t(x') - K_{x'x} p_t(x)\right] \log \frac{K_{xx'} p_t(x')}{K_{x'x} p_t(x)}}_{\dot{\Sigma}} $$ $$+ \underbrace{\frac{1}{2} \sum_{xx'} \left[K_{xx'} p_t(x') - K_{x'x} p_t(x)\right] \log \frac{K_{x'x}}{K_{xx'}}}_{\dot{\mathcal{E}}}$$

\( \dot{\Sigma} \geq 0 \)  entropy production rate (2nd law of TD)

\(\dot{\mathcal{E}} = \beta \dot{Q}\) entropy flow rate (connecting 1st and 2nd law quantities)

Stochastic thermodynamics

6.) Trajectory thermodynamics - consider stochastic trajectory

\(\pmb{x}= (x_0,t_0;x_1,t_1;\dots)\). Energy \(u_t(\pmb{x}) = u(\pmb{x}(t),\lambda(t))\)

\(\lambda(t)\) - control protocol

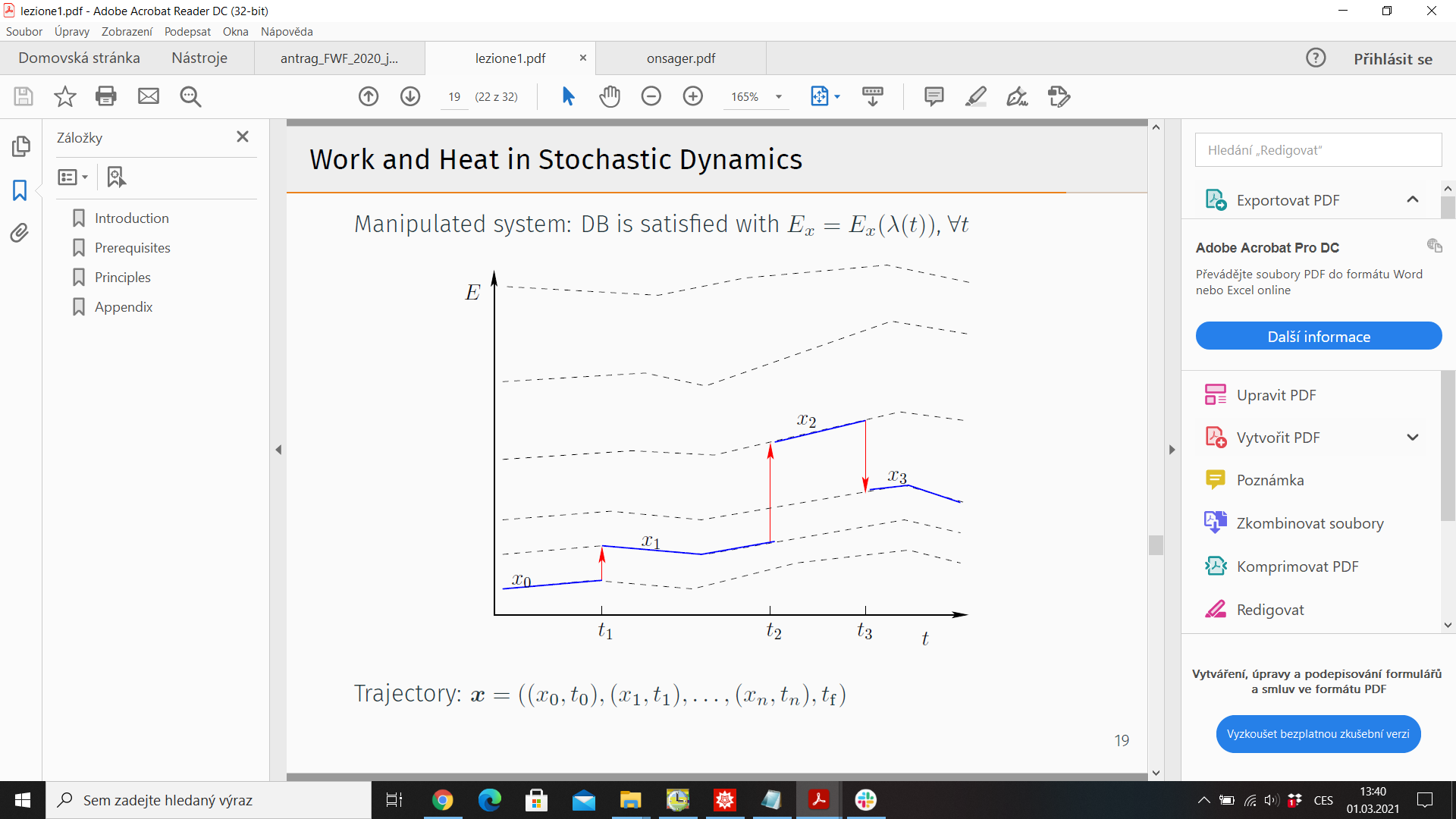
Probability of observing \( \pmb{x}\): \(\mathcal{P}(\pmb{x}\))

7.) Time reversal \(\tilde{\pmb{x}}(t) = \pmb{x}(T-t)\)

Reversed protocol \(\tilde{\lambda}(t) = \lambda(T-t)\)

Probability of observing reversed trajectory under reversed protocol \(\tilde{\mathcal{P}}(\tilde{\pmb{x}})\)

Stochastic thermodynamics

8.) Trajectory second law

Trajectory entropy: \(s_t(\pmb{x}) = - \log p_t(\pmb{x}(t)\)) 

Ensemble entropy: \(S_t = \langle s_t(\pmb{x}) \rangle_{\mathcal{P}(\pmb{x})} = \int \mathcal{D} \pmb{x} \mathcal{P}(\pmb{x}) s_t(\pmb{x})\)

Trajectory 2nd law \( \Delta s =   \sigma +  \epsilon\)

Trajectory EP: \(\sigma = \underbrace{\ln p_t(\pmb{x}(t)) - \ln p_0(\pmb{x}(0))}_{\Delta s} + \underbrace{\sum_{i=1}^M \ln \frac{K_{\pmb{x}_{T_i}\pmb{x}_{T_{i-1}}}}{\tilde{K}_{\pmb{x}_{T_{i-1}}\pmb{x}_{T_i}}}}_{-\epsilon}\)

Stochastic thermodynamics

9.) Detailed Fluctuation theorem

Relation to the trajectory probabilities

$$\log \frac{\mathcal{P}(\pmb{x})}{\tilde{\mathcal{P}}(\tilde{\pmb{x}})} =  \sigma$$

Detailed fluctuation theorem (DFT)

$$\frac{P(\sigma)}{\tilde{P}(-\sigma)} = e^{\sigma}$$

10.) Integrated fluctuation theorem 

By rearraning DFT we get \( P(\sigma) e^{-\sigma} = \tilde{P}(-\sigma)\)

By integrating over \(\sigma\), we obtain IFT

$$ \langle e^{- \sigma} \rangle = 1 \quad \stackrel{Jensen}{\Rightarrow} \langle \sigma \rangle =  \Sigma \geq 0$$

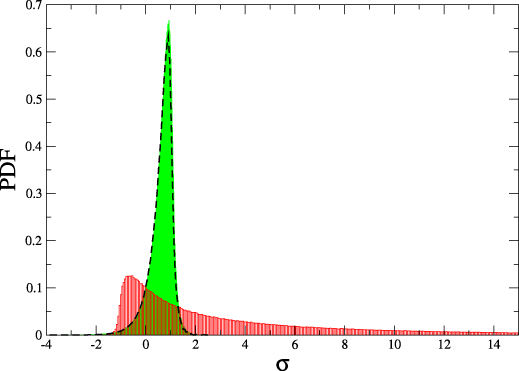
2nd law is consequence of FTs!

Stochastic thermodynamics in uncertain environment

Thermodynamics of systems coupled to uncertain environment

• Consider a set of apparatuses \(\mathcal{A}\).
• For each apparatus \(\alpha \in \mathcal{A}\), we have a system with a precise number of baths, temperatures, chemical potentials, etc. satisfying local detailed balance
• We consider a probability distribution \(P^\alpha\) over the apparatuses

Effective value over the apparatuses can be defined as 

$$ \overline{X}:= \int \mathrm{d} P^\alpha X^\alpha$$

Effective distribution \(\bar{p}_x(t)\) fulfills the equation

  \( \dot{\bar{p}}_x(t) = \sum_{x'} \int \mathrm{d} P^\alpha K^\alpha_{xx'} p^\alpha_{x'}(t) \)   which is generally non-Markovian

Effective ensemble stochastic thermodynamics

• Expected internal energy is \(\bar{U} = \int \mathrm{d} P^\alpha \sum_x p^\alpha_t(x) u^\alpha(x)\)
• Expected first law of thermodynamics

$$\dot{\bar{U}} = \dot{\bar{Q}} + \dot{\bar{W}}$$

• Expected ensemble entropy \(\bar{S} =  - \sum_x \int \mathrm{d} P^\alpha p_t^\alpha(x) \ln p_t^\alpha(x)\)
• Expected second law of thermodynamics $$\dot{\bar{S}} = \dot{\bar{\Sigma}} + \dot{\bar{\mathcal{E}}}$$
• \(\dot{\bar{\Sigma}} \geq 0\)

• \(\dot{\bar{\mathcal{E}}} = \overline{\beta \dot{Q}}\) - no explicit relation between \(\dot{\bar{\mathcal{E}}}\) and \(\dot{\bar{Q}}\)

Effective trajectory stochastic thermodynamics

• Effective trajectory entropy is defined as \(\overline{s}_t(\pmb{x}) = - \overline{\log p_t(\pmb{x}(t)}\))
• Ensemble average \( \langle \overline{s}_t(\pmb{x})\rangle_{\overline{\mathcal{P}}(\pmb{x})} \neq \bar{S}_t \equiv \overline{\langle s^\alpha_t(\pmb{x}) \rangle_{\mathcal{P}^\alpha(\pmb{x})}}\)
• In general, ensemble average and effective averaging do not commute
• As a consequence, the fluctuation theorems do not hold for \(\overline{\sigma}\)

Decomposition of effective EP

Denote \(\mathcal{P}^\alpha(\pmb{x}) \equiv \mathcal{P}(\pmb{x}|\alpha)\) and \(\mathcal{P}(\pmb{x},\alpha) = \mathcal{P}(\pmb{x}|\alpha) P^\alpha\)

Effective ensemble EP \(\bar{\Sigma}\) can be expressed as $$\bar{\Sigma} = \int \mathrm{d} P^\alpha \mathcal{D} \pmb{x} \, \mathcal{P}^\alpha(\pmb{x}) \sigma^\alpha(\pmb{x}) = \int \mathrm{d} \alpha \mathcal{D} \pmb{x} P^\alpha \mathcal{P}^\alpha(\pmb{x}) \ln \frac{\mathcal{P}^\alpha(\pmb{x}) P^\alpha}{\tilde{\mathcal{P}}^\alpha(\tilde{\pmb{x}}) P^\alpha}$$

$$= D_{KL}(\mathcal{P}(\pmb{x},\alpha)||\tilde{\mathcal{P}}(\tilde{\pmb{x}},\alpha)) $$

By using chair rule for KL-divergence

$$D_{KL}(\mathcal{P}(\pmb{x},\alpha)||\tilde{\mathcal{P}}(\tilde{\pmb{x}},\alpha)) = D_{KL}(\mathcal{P}(\pmb{x})||\tilde{\mathcal{P}}(\tilde{\pmb{x}})) + D_{KL}(\mathcal{P}(\alpha|\pmb{x})||\tilde{\mathcal{P}}(\alpha|\tilde{\pmb{x}}))$$

where \(\mathcal{P}(\pmb{x}) = \int \mathrm{d} \alpha \, P^\alpha \mathcal{P}(\pmb{x}|\alpha) \equiv \bar{\mathcal{P}}(\pmb{x})\) and \(\mathcal{P}(\alpha|\pmb{x}) = \frac{\mathcal{P}(\pmb{x}|\alpha) P^\alpha}{\mathcal{P}(\pmb{x})}\)

Phenomenological EP

Phenomenological EP \(\underline{\Sigma} = D_{KL}(\mathcal{P}(\pmb{x})||\tilde{\mathcal{P}}(\tilde{\pmb{x}})) = \int \mathcal{D} \pmb{x} \mathcal{P}(\pmb{x}) \ln \frac{\mathcal{P}(\pmb{x})}{\tilde{\mathcal{P}}(\tilde{\pmb{x}})}\)

Phenomenological trajectory EP is \(\underline{\sigma} = \ln \frac{\mathcal{P}(\pmb{x})}{\tilde{\mathcal{P}}({\tilde{\pmb{x}}})}\)

It is straightforward to show that \(\underline{\sigma}\) fullfills detailed fluctuation theorem

$$ \frac{P(\underline{\sigma})}{\tilde{P}(-\underline{\sigma})} = e^{\underline{\sigma}}$$

Phenomenological EP describes thermodynamics for the case of expected probability

It is a lower bound for the effective EP: \(\overline{\Sigma} \geq \underline{\Sigma}\)

Inference EP

Inference EP \(\Omega = D_{KL}(\mathcal{P}(\alpha|\pmb{x})||\tilde{\mathcal{P}}(\alpha|\tilde{\pmb{x}})) = \int \mathrm{d} P^\alpha \mathcal{P}(\alpha|\pmb{x}) \ln \frac{\mathcal{P}(\alpha|\pmb{x})}{\tilde{\mathcal{P}}(\alpha|\tilde{\pmb{x}})}\)

Inference trajectory EP as \(\omega:= \sigma^\alpha - \underline{\sigma} =  \ln \frac{\mathcal{P}(\alpha|\pmb{x})}{\tilde{\mathcal{P}}(\alpha|\tilde{\pmb{x}})}\)

We can also show that \(\omega\) fulfills Detailed FT:

$$\frac{P(\omega|\pmb{x})}{\tilde{P}(-\omega|\tilde{\pmb{x}})} = e^{\omega}  $$

From Integrated FT, we obtain that \(\Omega_{\pmb{x}} = \langle \omega \rangle_{P(\omega|\pmb{x})} \geq 0\)

Interpretation: \(\Omega\) is the average rate of how much information we gain from Bayesian inference of \(P(\alpha)\) from observing \(\pmb{x}\)

Interpretation of phenomenological EP

Let us consider \(\pmb{x}_t\) as a part of trajectory \(\pmb{x}\) from 0 to t.

Define \(\underline{X}_t := \int \mathrm{d} \alpha  \mathcal{P}(\alpha|\pmb{x}_t) X^\alpha\)

Then we can show that 

$$\underline{\sigma} = \underbrace{\ln \underline{p}_t(x(t)) - \ln \underline{p}_0(x_0)}_{\Delta \underline{s}} + \underbrace{\sum_{i=1}^M \ln \frac{\underline{K}_{\pmb{x}_{T_i}\pmb{x}_{T_{i-1}}}}{\tilde{\underline{K}}_{\pmb{x}_{T_{i-1}} \pmb{x}_{T_i}}}}_{-\underline{\epsilon}} $$ 

We can effectively treat the non-Markovian model with uncertain \(\alpha\) as Markovian model with trajectory-dependent distribution \(\mathcal{P}(\alpha|\pmb{x}_t)\)

Example:

two-state system with uncertain temperature

Two-state CTMC with unknown temperature

\(E_0\)

\(E_1\)

consider \(E_1 > E_0\)

Consider transition rates:

\(K_{0 \rightarrow 1} = e^{-\beta(E_0-E_1)/2}\)

\(K_{1 \rightarrow 0} = e^{-\beta(E_1-E_0)/2}\)

The rates satisfy detailed balance

Let us assume that we do not know the inv. temperature \(\beta\)

Two-state CTMC with unknown temperature

We observe a trajectory \(\pmb{x}\)

According to the waiting times, we can calculate \(\mathcal{P}(\beta|\pmb{x}_t)\) for times

\(t = \{T_1,T_2,T_3\}\)

Updating of \(P(\beta) \mapsto P(\beta|\pmb{x}_t)\)

from observing \(\pmb{x}_t\)

Text

True value: \(\beta^\star = 1\)

Updating of \(P(\beta) \mapsto P(\beta|\tilde{\pmb{x}}_t)\)

from reversed dynamics

Trajectory Inference EP

\(\Omega_{\pmb{x}_t}\) increases in time

There is more!

• Maximal work extractions with uncertain temperatures
• Dynamic of the thermodynamic value of information                    

Possible extensions:

• Systems with uncertain energy spectrums
• Experiments with uncertain control protocols
• Complete analysis of maximal work extraction to reach a target distribution with a given probability measure, both when one can specify aspects of the evolution (e.g., a quenching Hamiltonian) and when  one can only specify it up to a given precision.

Thanks!