Stochastic thermodynamics of computation
Jan Korbel
CSH Workshop "Computation in dynamical systems", Obergurgl
slides available at: www.slides.com/jankorbel
Why should we care about thermodynamics of computation?
- Computers consume 6-10% of total electricity
- A part of the energy is inevitably transferred to a waste heat
- Most research in CS has been focused on the performance of the computation, not taking into account the costs
- A little is known about whether and how the energetic costs can be eliminated

Fundamental costs of computing
- The fundamental question is what are the inevitable costs of computation and what costs can be mitigated
- The notoriously known is the Landauer's bound $$Q \geq - k T \Delta S$$
- Originally, it was used to lower-bound the dissipated heat of a bit eraser. The eraser changes the initial distribution \(\{1/2,1/2\}\) to the final distribution \(\{1,0\}\), so \(\Delta S = - \ln 2\) and we obtain the famous formula $$Q \geq k T \ln 2$$
General form of Landauer's bound
- More generally, the Landauer's bound is a direct consequence of the second law of thermodynamics
- A central quantity in non-equilbrium thermodynamics is the entropy production $$\sigma = \Delta S + \sum_i \frac{Q_i}{k T_i}$$
- The main property of the entropy production is that it cannot be negative, i.e., \(\sigma \geq 0\)
- From this, we obtain that $$ \sum_i \frac{Q_i}{k T_i} > - \Delta S$$
- Typically the computation is designed to lower the entropy, so we get a strictly positive bound on the dissipated heat
Parallel 2-bit eraser
- What is Landauer's cost of the simultaneous erasure of two bits \(B_{1,2}\) with initial marginal distributions \(\{1/2,1/2\}\)?
- Naively, one can think that it is \( 2 kT \ln 2\) because we erase two bits
- By using the general formula, the cost is the drop in the joint entropy of the two bits.
- The initial joint entropy can be expressed as $$S(B_1,B_2) = S(B_1) + S(B_2) + I(B_1,B_2)$$ where \(S(B_{1,2}) =- \ln 2\) is the entropy of the marginal initial distribution and \(I(B_1,B_2)\) is the mutual information
- Thus, the landauer cost can be expressed as $$Q \geq kT 2 \ln 2 + k T I(B_1,B_2)$$
- The mutual information is a special case of a mismatch cost

Parallel 2-bit eraser
Logical and thermodynamic reversibility
- In the previous decades, there has been a debate about the relationship of logical reversibility and thermodynamic reversibility
- Logical reversibility: a computation is logically reversible if and only if, for any output logical state, there is a unique input logical state.
- Thermodynamic reversibility: a process is thermodynamically reversible if and only if the entropy production is equal to zero (quasi-static process)
- Historically, some authors were pointing out a relation between logical and thermodynamic reversibility
- However, several papers have shown that logical and thermodynamic (ir)reversibility are, in fact, completely independent properties of a physical process
Logical and thermodynamic reversibility

| Initial value bit | Final value bit |
|---|---|
| 1 | 0 |
| 0 | 0 |
Example 1: bit erasure
Example 2: measurement
| Initial value system | Inivial value m. device | Final value system | Final value m. device |
|---|---|---|---|
| 1 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 |
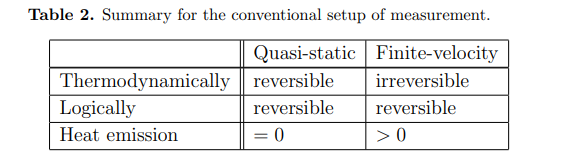
Relevance of Landauers bound
- While Landauer bound gives us a fundamental bound of computation, it is well known that the actual computers, both artificial and natural, dissipate much more energy than Landauer's bound predicts
- Even for a bit erasure, the bound can only be achieved by a quasistatic process (that takes infinite time) and with the optimal protocol
- Real computers are designed to compute in finite time and do much more than just a bit erasure
- In general, physical constraints of computers lead to increased heat dissipation
Stochastic thermodynamics
- Since real computations are performed in finite time, using the framework of equilibrium thermodynamics is not sufficient for characterizing the thermal dissipation of computation
- Thus, it is necessary to use another framework that can incorporate the far-from-equilibrium dynamics of computation
- Stochastic thermodynamics provides us with powerful tools that enable to connect the theory of stochastic processes to far-from-equilibrium thermodynamics
Stochastic thermodynamics
- Stochastic thermodynamics is a field that emerged in 90's
- Its original application was in non-equilibrium thermodynamics of mesoscopic systems, as chemical reaction networks and molecular motors
- Probably the most popular result are the fluctuation theorems extending the validity of the 2nd law of thermodynamics to the case trajectory quantities
- The direct corollaries as Crooks fluctuation theorem and Jarzynski equality relate work done on a system with the free energy difference

Fluctuation theorems
Mismatch cost
- In the previous example, we observed a special case of a mismatch cost
- The mismatch cost is an additional term to the entropy production caused by the fact that the control protocol of a process was designed to optimize a (computation) process given the particular initial distribution but the actual distribution is different
- Consider a physical process with initial distribution \(q_{t_0}(x)\) that minimizes the entropy production
- The actual initial distribution is \(p_{t_0}(x)\)
- The EP can be then expressed as $$\sigma(p_{t_0}) = \sigma(q_{t_0}) + D_{KL}(p_{t_0}\|q_{t_0}) - D_{KL}(p_{t_f} \| q_{t_f})$$
- \(D_{KL}(p\|q) = \sum_x p(x) \log \frac{p(x)}{q(x)}\) is the Kullback-Leibler divergence
Mismatch cost for a 2-bit eraser
- In the case of a 2-bit eraser, \(q_{t_0}(B_1,B_2) = p_{t_0}(B_1) p_{t_0}(B_2)\) and therefore
$$D_{KL}(p_{t_0}(B_1,B_2)\|p_{t_0}(B_1) p_{t_0}(B_2)) = I(B_1,B_2)$$
- This particular type of mismatch cost is called modularity cost which is the cost for the fact that the subsystems are statistically coupled
- Therefore, each time a system is build from two or more statistically coupled subsystems (which is a typical setup in all computational devices) we pay an extra cost
Speed limit theorems
$$ \sigma (\tau) \geq\frac{\left(\sum_x |p_0(x) -p_\tau(x)|\right)^2}{2 A_{\text{tot}}(\tau)}$$
- Another aspect of computation is the time of computation
- One could expect that faster computation leads to more dissipated heat
- The lower bound is provided by the speed limit theorem which can be formulated as
where \(p_0\) is the initial distribution, \(p_{\tau}\) is the final distribution, and \(A_{tot}\) is the total activity which is the average number of state transitions that occur during the computational process.
- The term in the enumerator is the square of the \(L_1\) distance between the initial and the final state
Thermodynamic uncertainty relation
$$\sigma (\tau) \geq \frac{2 \langle J (\tau) \rangle^2}{\mathrm{Var}(J (\tau))} $$
- Another contribution to the EP is due to the cost of precision
- Suppose we choose an increment function \(d(x', x)\). Such a function can be any observable, real-valued function of state transitions \(x' \to x\) that is anti-symmetric under the interchange of its two arguments.
- The current \(J\) associated with that function is the value of the associated observable summed over all state transitions in a trajectory.
- The entropy production can be then lower-bounded by the normalized precision of a current

SLT & TUR

Example: two equivalent circuits
\(\sum_x |p_i(x) - p_f(x)| = 3/8\)
Initial distribution: input states - uniform, internal states - 0
\(\sum_x |p_i(x) - p_f(x)| = 6/8\)
Possible consequences for CS
- In theoretical CS, a computational device is typically an abstract, generic model of any entity that computes (transforms an input into an output)
- We think about computation in an abstract way: we count the number of operations and how they scale
- In applied CS, the programmers are also thinking about other costs, runtime, memory, etc.
- Similarly, we can think about other costs as dissipated energy

Mapping between design features of a computer and its performance through resource costs
Possible consequences for CS
- Depending on the particular task, the amount of dissipated heat can depend not only on theoretical computation but also on the physical representation of the computational device
- It is not only the architecture of the computational devide, but the physical substrate and representation of computational states that can have a large impact

Probabilistic computation
- One possible example of a non-conventional approach to computation is the probabilistic computation
- Similarly to quantum computation, one might generalize the standard binary representation of the information to a probabilistic representation
- This approach might be useful when dealing with stochastic problems (MC simulations, Bayesian networks, Markov models)
- Probabilistic computing has a wide range of applications, including machine learning, robotics, computer vision, natural language processing, and cognitive computing.
Neuromorphic computing
- Another example of a non-conventiional computation approach is neuromorphic computing
- Here, contrary to standard CMOS-based computers, the architecture is inspired by the structure and function of the human brain
- While this approach might be useful in specific computation tasks, it might be also more energetically favorable

Conclusions
- Thermodynamics of Computation is an important aspect of CS
- It is important to understand which energetic costs are fundamental and which can be optimized by using different approaches (algorithms, architecture, physical representation)
- Non-conventional approaches to computation (that are also the topic of this workshop) can have important consequences to thermodynamics of computation
More resources
- David's review paper: J. Phys. A: Math. Theor. 52 193001
- David's lectures on YouTube
- Perspective paper (in prep)
Stochastic thermodynamics of computation
By Jan Korbel
Stochastic thermodynamics of computation
- 302



