S1 Statistics Probability
By Jay Teach
S1 Statistics Probability
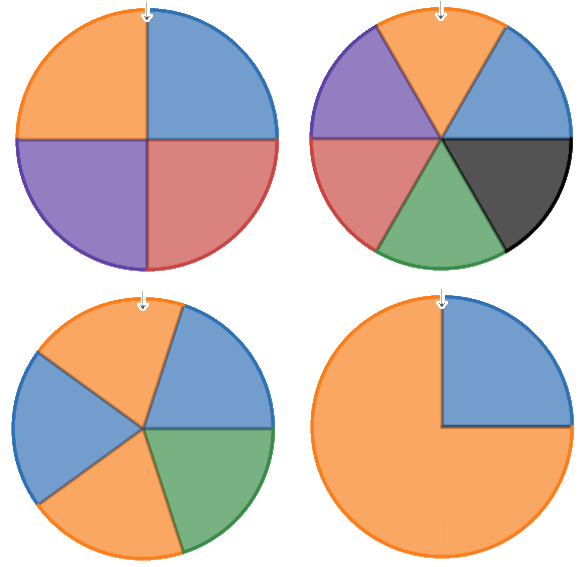
·# Probability Number Line [Drawn on Board] (Exciting Vegas Cover Picture) · ·impossible unlikely even 50/50 likely certain ·0 0.5 1 ·A B C D E F G · ·# Describing Probability with Words (Qualitative) ·An event's probability is a prediction of how LIKELY it is to occur e.g. ·impossible unlikely even 50/50 likely certain · ·# Estimate the Likleyhood of Different Events ·https://www.menti.com/hpippc1cdf ·1. P(A bus stops in George Street within 10mins) ·2. P(you see a bright pink Lamborghini in a car park) ·3. P(an equilateral triangle has a 60° angle) ·4. P(the next baby born in a family is a girl) ·5. P(Saturday is 3 days after Tuesday) ·6. P(it rains on at least 1 day in April) ·7. P(a wife is taller than her husband) ·Answers: 1. E 2. B 3. G 4. D 5. A 6. F 7. C ·Invent your own events. Locate their probability on the scale using words, numbers, and labels · ·# Describing Probability with Numbers (Quantitative) ·It is a number between 0–1, with no units. ·It can be written as a percentage, or more commonly as fraction or decimal. ·Express probabilities as 1/2 (0.5) rather than "1 in 2", because a probability is always a number in-between or equal to 0 or 1 ·This is a fraction, we should always simplify fractions (e.g. the probability 6/15 = 2/5) · ·# Calculate Probabilities Using Frequency ·To compare probabilities, we need a fair way to measure them (to put numbers on them). ·Probability = P(number of the events we want) / P(number of all the possible events) · ·# Examples of Counting the Number of Possible Cases (Quickly with Show-Me Boards) ·Coin flip / Dice / Egg Cartons / Truck Wheels / Different Spinners · ·# How to Write Probability Equations ·We can write a probability in an equation: ·"The probability of event 'X' happening is 1." ·becomes: "P(event 'X') = 1" ·Or even shorter: P(X)=1 · ·# Probability of Rolling a 6 on a Cube ·There is only one '6' out of the 6 sides of a dice, there is only one 'blue' side on a fully-solved Rubik's cube. [Roll a cube around as an example of a large dice]. · ·# Exercise 2 page 161 Questions 1-6 · ·# Easier vs. Harder Dice Games ·Take a dice game where you win if you roll 5 or 6, and lose otherwise. Is it more likely to win this game or to lose it? [2 cases / 6 possible] ·Compare this probability to a game where you only win if you roll a 6. · 2/6 > 1/6 · 1/3 > 1/6 ·33.3% > 16.67% · ·# Opposite Probabilities ·If P(A) is the probability that A happens, the opposite probability (the probability that A does NOT happen) is calculated using 1-P(A) . ·Page 161 Question 6: 4 marbles, 1 blue 3 red. P(red)+P(blue)=1 so P(blue)=1-P(red)=1-3/4=1/4 · ·# Probability Kahoot https://create.kahoot.it/details/probability/cab63a54-cac7-41d1-9e46-72f5235e800d