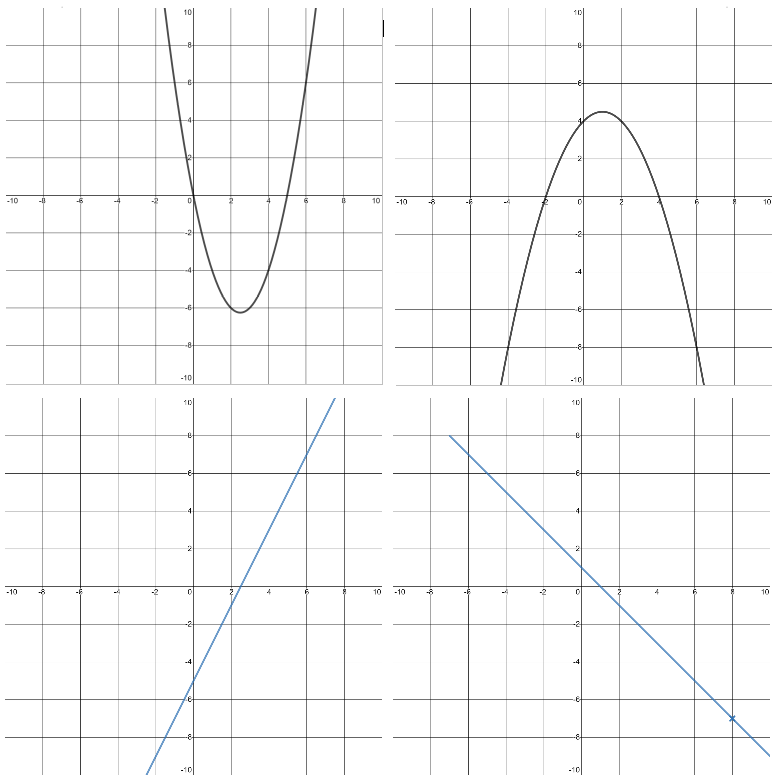
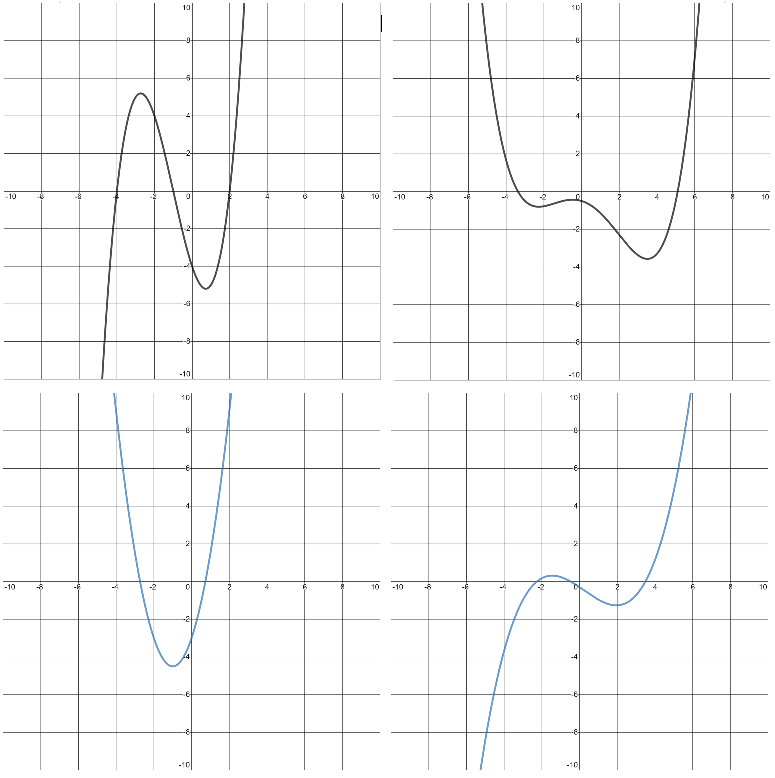
S5 Calculus Curve Table Min Max
By Jay Teach
S5 Calculus Curve Table Min Max
·Understand the relation between the shape of \(f’(x)\) and \(f(x)\), how one connects with the other. · ·Can plot Curve Tables of functions to identify their shape, and can use these to plot the graph of \(f’(x)\) for a given \(f(x)\). ·S5 Class, 2x40min period, end of day, 3 days in a row, usually quite tired. · ·Heinemann Higher Mathematics textbook Chapter6 pg105–111. https://is.gd/ea_21 ·Slides: https://slides.com/jayteach/s5_calc_min_max/fullscreen/ Desmos:https://www.desmos.com/calculator/fxglkpqt4p · · ·# Review yesterday’s content and feedback: · ·# Every value of \(a\) that makes \(f’(a)=0\) is called a “stationary point” · ·When \(f’(x)\) is negative, \(f(x)\) is decreasing. ·When \(f’(x)\) is \(0, f(x)\) is stationary. ·When \(f’(x)\) is positive, \(f(x)\) is increasing. · ·Minimum: - 0 + “min” for “minus” Maximum: + 0 - “max” has ‘x’→ ‘+’ · \ _ / / ‾ \ · ·Steps for Constructing ‘Curve Tables” to Analyze Graphs using the Derivative Graph: ·1. Differentiate ·2. Solve for Zeroes ·3. Assign sign of zones (by plugging-in values, visually from the graph, or from patterns) ·4. Identify as either minimum, maximum, or turning point. ·Use DESMOS to help visualize things · ·# ·pg104 Exercises 6L 2–8 finding where functions are positive/negative · ·The parabola \(f(x)=x^2-5x\) differentiates to \(f’(x)=2x-5\), with maximum at \(x=\frac{5}{2}\). ·The parabola \(f(x)=-\frac{1}{4}(x+2)(x-4)\) differentiates to \(f’(x)=-\frac{1}{2}x+\frac{1}{8}\), with maximum at \(x=1\). [Annotate Printout side 1] · ·# ·To sketch the graph of \(f’(x)\) from \(f(x)\): ·1. Find the stationary and turning points, ·2. Assign the sign for each zone, and ·3. Connect-up all the details. [Annotate Printout side 2] · ·pg110 Exercises 6P sketching graph of derivatives · ·# Same feedback questions as yesterday: Assess self-reported confidence in: ·●Pairing up a particular graph with its derivative graph. ·●Identifying where f’(x) is +,-,0 just by looking at f(x). ·●Sketching f'(x) just by looking at f(x). ·●Using f(x) to explain what happens in f’(x). ·●Using f'(x) to explain what happens in f(x). ·●Using the equation for f'(x) to calculate the rate of change of f(x) at different places.