Jason Dobry
Husband. Father. Software Engineer. Open Source hacker. Always learning.
Make Dat Money
TDF
By Jason Dobry
Problem #1
Need Clean Data
Inconsistent intervals,
crazy numbers in off ours, etc.
Solution
Clean it
Gathered data every hour on the hour from operational hours
Problem #2
Predicting Returns
Predict next hourly data point?
Or predict opening value?
Closing value?
Um, how?
Attempt #1
L2 Regression
Example
Fail
Heavily affected by outliers,
non-linearity,
too many variables, etc.
Attempt #2
Kalman Filter
What's that?
The Gist
The Kalman filter operates recursively on streams of noisy input data to produce a statistically optimal estimate of the underlying system state.
Applications
Autopilot
Tracking and Vertex Fitting of charged particles in Particle Detectors
Tracking of objects in computer vision
Economics, in particular macroeconomics, time series, and econometrics
Inertial guidance system
Orbit Determination
Radar tracker
Dynamic positioning &
Navigation systems
Seismology
Simultaneous localization and mapping
Speech enhancement, Weather forecasting, 3D modeling
Example
How does it work?
xt = A * (xt - 1) + w
xt -
hidden variable we're trying to estimate
A - state transition matrix
(xt - 1) -
current state
w -
noise of model
zt = H * xt + v
zt - noisy measurement
H -
observation model
xt -
xt from above
v -
noise of model
How does it work?
xt = A * (xt - 1) + w
xt -
hidden variable we're trying to estimate
A - state transition matrix
(xt - 1) -
current state
w -
noise of model
zt = H * xt + v
zt - noisy measurement
H -
observation model
xt -
xt from above
v -
noise of model
Quadratic Filter
xk | k-1 = 3 (xk-1 - xk-2) + xk-3
assumes that every four consecutive trend values fit a quadratic curve
xk = xk | k-1 + ( Gk * (yk - xk | k-1) )
final estimate combines observation and state change estimate
Problem #3
Risk
Solution
Force Diversification
Restrict Maximum amount of wealth invested per stock
Experiments
Restrict investment per stock to:
1% of wealth
5% of wealth
20% of wealth
Solve LP for Optimal Portfolio
Trade = Optimal Portfolio - Current Portfolio
Experiments
Trade:
Every Hour
At Opening
At Closing
Most successful agents had diverse portfolios and traded once a day
Make Dat Money
By Jason Dobry
Make Dat Money
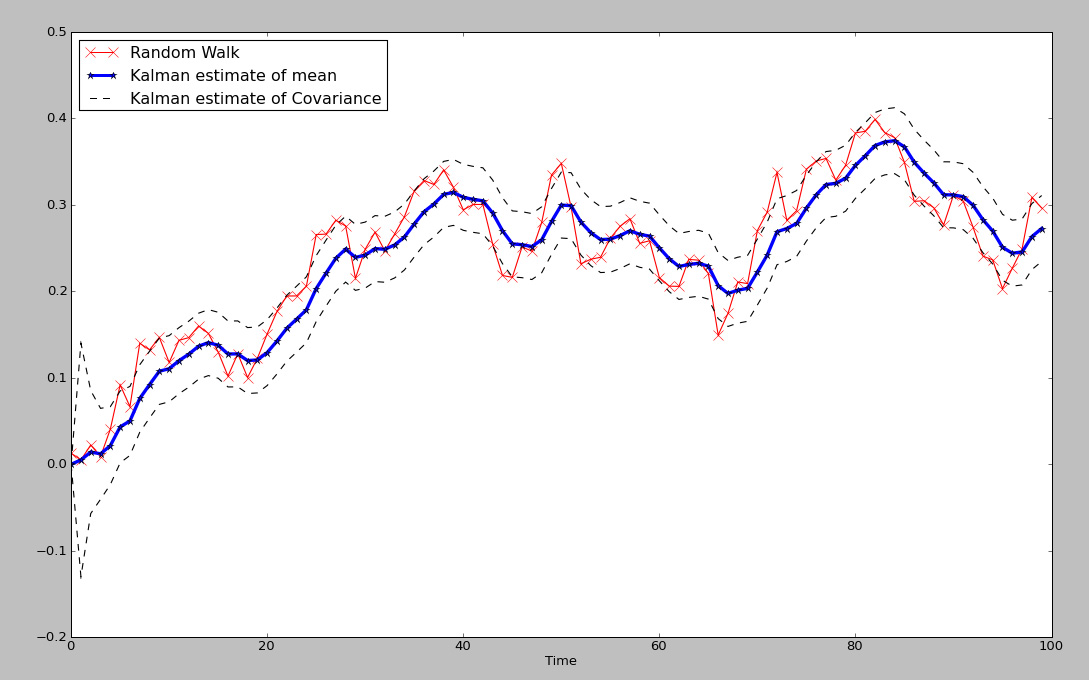
Portfolio Optimization with Kalman Filters
