From Data to Insights
Jeremias Sulam
Trustworthy methods for modern biomedical imaging


ARISE Network Virtual Meeting

50 years ago ...
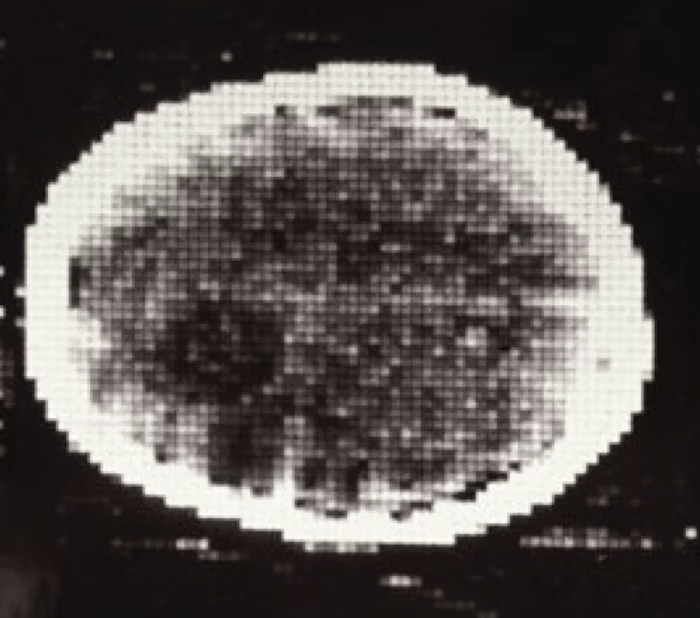
first CT scan


ELECTRIC & MUSICAL INDUSTRIES
50 years ago ...

imaging
diagnostics
complete hardware & software description
human expert diagnosis and recommendations

imaging was "simple"
... 50 years forward

Data

Compute & Hardware



Sensors & Connectivity







Research & Engineering
... 50 years forward

Data

Compute & Hardware



Sensors & Connectivity







Research & Engineering


data-driven imaging
automatic analysis and rec.
societal implications


data-driven imagingautomatic analysis and rec.societal implicationsProblems in trustworthy biomedical imaging
inverse problems
uncertainty quantification
model-agnostic interpretability
robustness
generalization
policy & regulation
Demographic fairness
hardware & protocol optimization



inverse problems
uncertainty quantification
model-agnostic interpretability
robustness
generalization
policy & regulation
Demographic fairness
hardware & protocol optimization
data-driven imaging
automatic analysis and rec.
societal implications
Problems in trustworthy biomedical imaging



Demographic fairness
Inputs (features): \(X\in\mathcal X \subset \mathbb R^d\)
Responses (labels): \(Y\in\mathcal Y = \{0,1\}\)
Sensitive attributes \(Z \in \mathcal Z \subseteq \mathbb R^k \) (sex, race, age, etc)
\((X,Y,Z) \sim \mathcal D\)
Eg: \(Z_1: \) biological sex, \(X_1: \) BMI, then
\( g(Z,X) = \boldsymbol{1}\{Z_1 = 1 \land X_1 > 35 \}: \) women with BMI > 35
Goal: ensure that \(f\) is fair w.r.t groups \(g \in \mathcal G\)
Demographic fairness
Group memberships \( \mathcal G = \{ g:\mathcal X \times \mathcal Z \to \{0,1\} \} \)
Predictor \( f(X) : \mathcal X \to [0,1]\) (e.g. likelihood of X having disease Y)
-
Group/Associative Fairness
Predictors should not have very different (error) rates among groups
[Calders et al, '09][Zliobaite, '15][Hardt et al, '16]
-
Individual Fairness
Similar individuals/patients should have similar outputs
[Dwork et al, '12][Fleisher, '21][Petersen et al, '21]
-
Causal Fairness
Predictors should be fair in a counter-factual world
[Nabi & Shpitser, '18][Nabi et al, '19][Plecko & Bareinboim, '22]
-
Multiaccuracy/Multicalibration
Predictors should be approximately unbiased/calibrated for every group
[Kim et al, '20][Hebert-Johnson et al, '18][Globus-Harris et at, 22]
Demographic fairness
-
Multiaccuracy/Multicalibration
Predictors should be approximately unbiased/calibrated for every group
[Kim et al, '20][Hebert-Johnson et al, '18][Globus-Harris et at, 22]
Demographic fairness
Observation 1:
measuring (& correcting) for MA/MC requires samples over \((X,Y,Z)\)
Definition: \(\text{MA} (f,g) = \big| \mathbb E [ g(X,Z) (f(X) - Y) ] \big| \)
\(f\) is \((\mathcal G,\alpha)\)-multiaccurate if \( \max_{g\in\mathcal G} \text{MA}(f,g) \leq \alpha \)
Definition: \(\text{MC} (f,g) = \mathbb E\left[ \big| \mathbb E [ g(X,Z) (f(X) - Y) | f(X) = v] \big| \right] \)
\(f\) is \((\mathcal G,\alpha)\)-multicalibrated if \( \max_{g\in\mathcal G} \text{MC}(f,g) \leq \alpha \)


Observation 2: That's not always possible...


Observation 2: That's not always possible...
sex and race attributes missing
- We might want to conceal \(Z\) on purpose, or might need to
We observe samples over \((X,Y)\) to obtain \(\hat Y = f(X)\) for \(Y\)
Fairness in partially observed regimes
\( \text{MSE}(f) = \mathbb E [(Y-f(X))^2 ] \)
A developer provides us with proxies \( \color{Red} \hat{g} : \mathcal X \to \{0,1\} \)
\( \text{err}(\hat g) = \mathbb P [({\color{Red}\hat g(X)} \neq {\color{blue}g(X,Z)} ] \)
[Awasti et al, '21][Kallus et al, '22][Zhu et al, '23][Bharti et al, '24]
Question
Can we (how) use \(\hat g\) to measure (and correct) \( (\mathcal G,\alpha)\)-MA/MC?
Fairness in partially observed regimes
Theorem [Bharti, Clemens-Sewall, Yi, S.]
With access to \((X,Y)\sim \mathcal D_{\mathcal{XY}}\), proxies \( \hat{\mathcal G}\) and predictor \(f\)
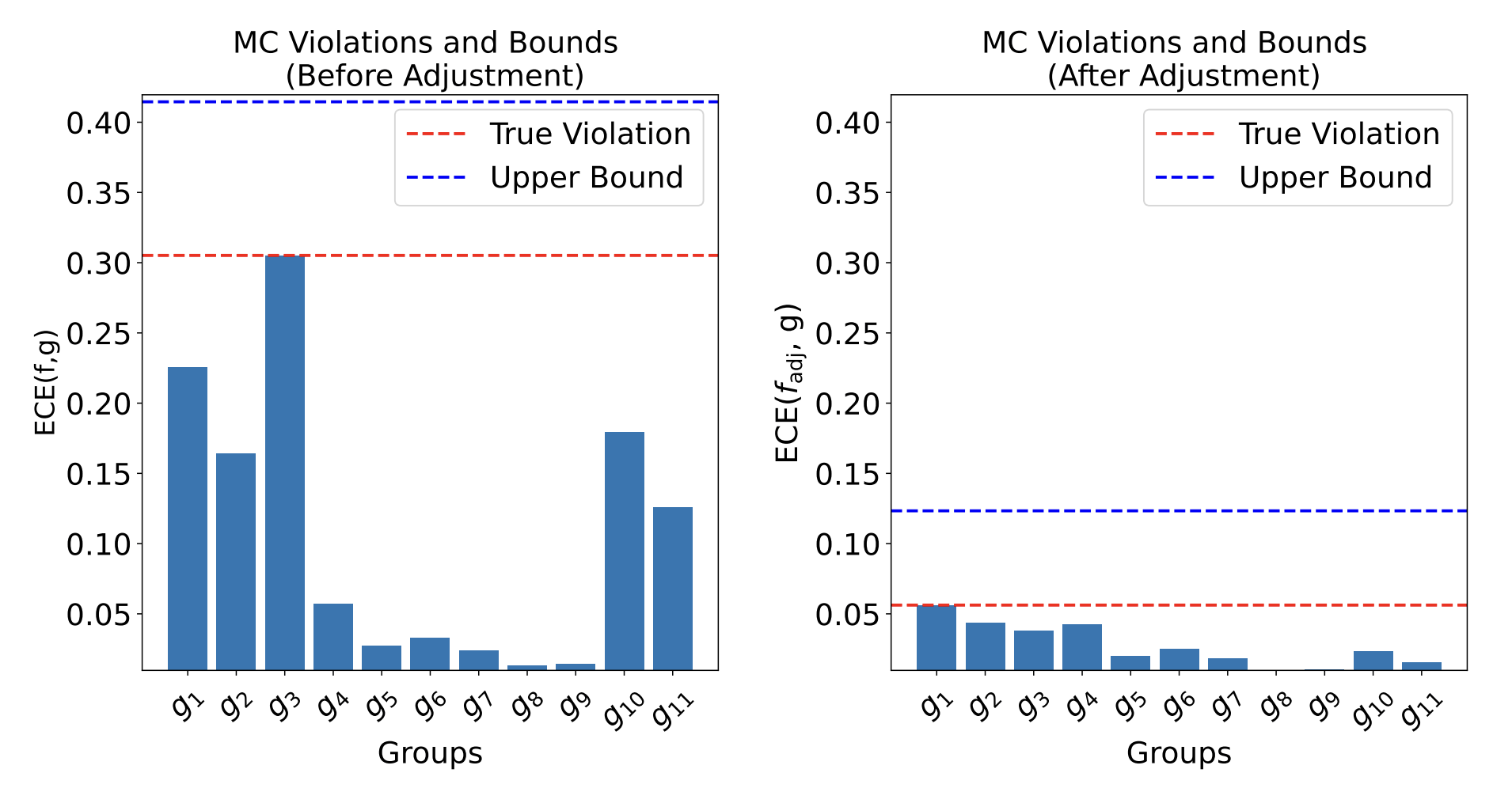
\[ \max_{\color{Blue}g\in\mathcal G} MC(f,{\color{blue}g}) \leq \max_{\color{red}\hat g\in \hat{\mathcal{G}} } B(f,{\color{red}\hat g}) + MC(f,{\color{red}\hat g}) \]
with \(B(f,\hat g) = \min \left( \text{err}(\hat g), \sqrt{MSE(f)\cdot \text{err}(\hat g)} \right) \)
- Practical/computable upper bounds \(\)
- Multicalibrating w.r.t \(\hat{\mathcal G}\) provably improves upper bound
[Gopalan et al. (2022)][Roth (2022)]
true error
worst-case error
Fairness in partially observed regimes
CheXpert: Predicting abnormal findings in chest X-rays
(not accessing race or biological sex)
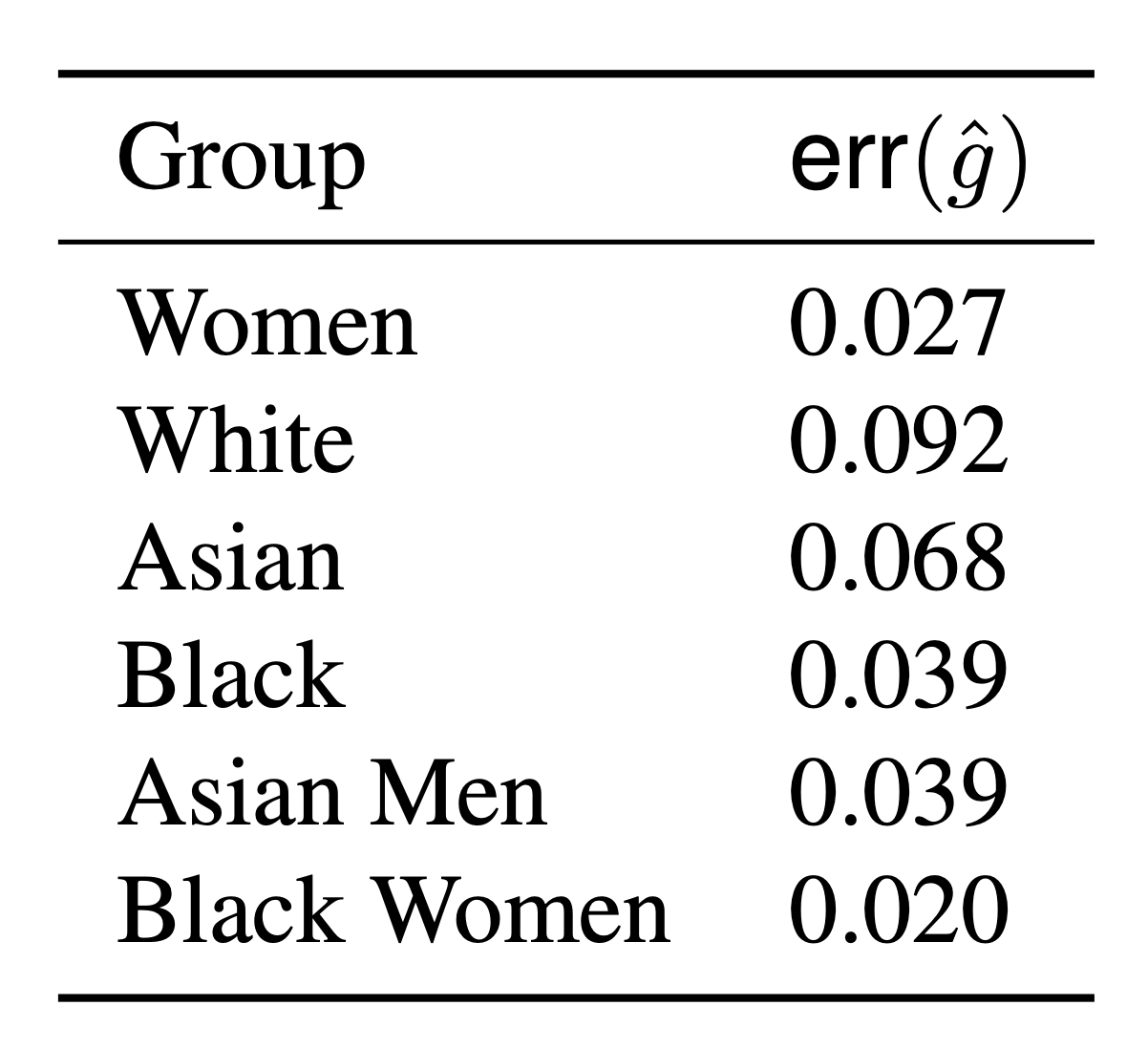
\(f(X): \) likelihood of \(X\) having \(\texttt{pleural effusion}\)
Demographic fairness
Take-home message
- Proxies can be very useful in certifying max. fairness violations
- Can allow for simple post-processing corrections





Thanks to the ARISE Community!

ARISE 2025
By Jeremias Sulam
ARISE 2025
- 70



