Yes, my network works!
Jeremias Sulam
... but what did it learn?
Biomedical Engineering Seminar
Yale University
"The biggest lesson that can be read from 70 years of AI research is that general methods that leverage computation are ultimately the most effective, and by a large margin. [...] Seeking an improvement that makes a difference in the shorter term, researchers seek to leverage their human knowledge of the domain, but the only thing that matters in the long run is the leveraging of computation. [...]
We want AI agents that can discover like we can, not which contain what we have discovered."The Bitter Lesson, Rich Sutton 2019
What did my model learn?
PART I
Inverse Problems
PART II
Image Classification
Two vignettes on medical imaging
Inverse Problems
y = A x^* + v
measurements
\hat x = \arg\min_x \frac 12 \| y - A x \|^2_2 + R(x)
reconstruction
Inverse Problems
y = A x^* + v
measurements
\hat x = \arg\min_x \frac 12 \| y - A x \|^2_2 + R(x)
reconstruction
= \arg\min_x ~-\log p(y|x) - \log p(x)
= \arg\max_x~ p(x|y)
\text{MAP estimate when }R(x) \propto -~p_x(x):\text{ prior}
Magnetic Susceptibility Imaging
\bar{M} = \chi \bar{H}
degree to which a material is magnetized when placed in a magnetic field
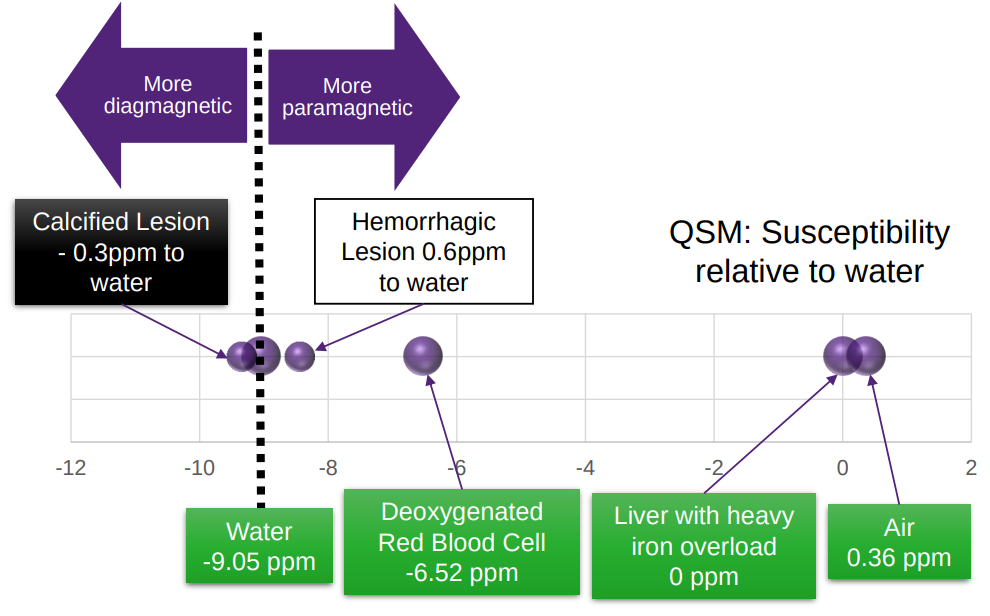
[from talk by S. Bollmann]
- Heme Iron (in RBC)
paramagnetic
- Myelin
diamagnetic
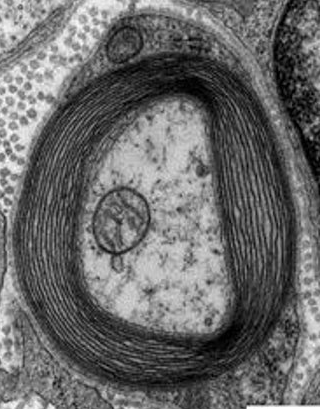
- Very important implications for neurodegenerative disorders
[Li et al, 2012]
Magnetic Susceptibility Imaging
Calculation of susceptibility through multiple orientation sampling (COSMOS)
[Liu et al, 2009]
As close as possible to "ground truth" in vivo
Impractical in the clinic
A{x} + v = y :
A'x + v' = y' :
A'x + v'' = y'' :
\hat x = \arg\min_x \frac 12 \| y - Ax \|^2_2 + R(x)
dipole inversion via
Image Priors
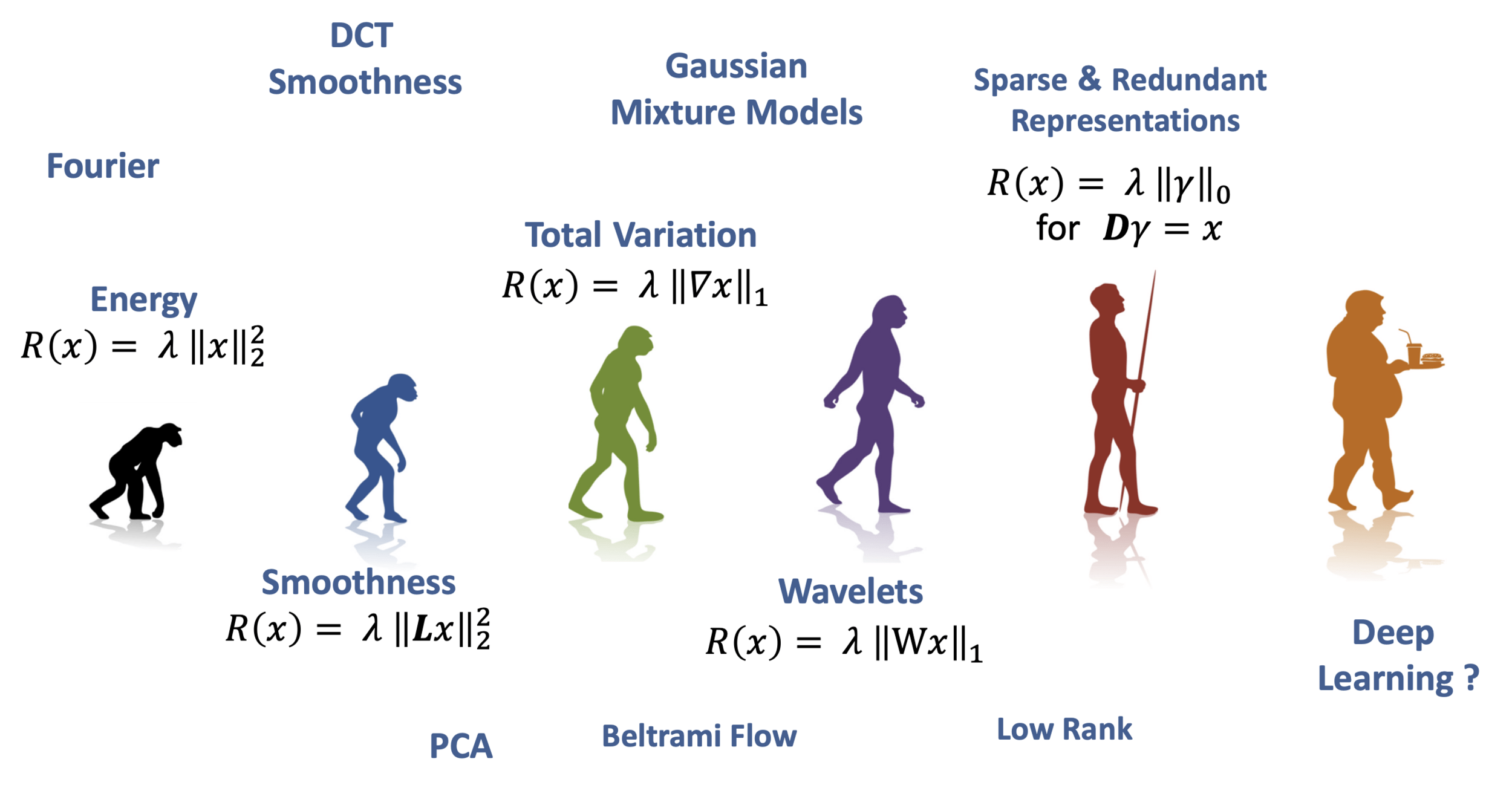
Deep Learning in Inverse Problems
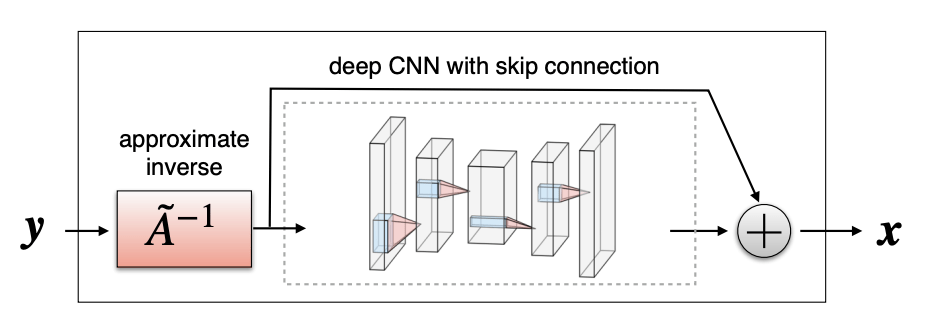
Option A: One-shot methods
Given enough training pairs \({(x_i,y_i)}\) train a network
\(f_\theta(y) = g_\theta(A^+y) \approx x\)
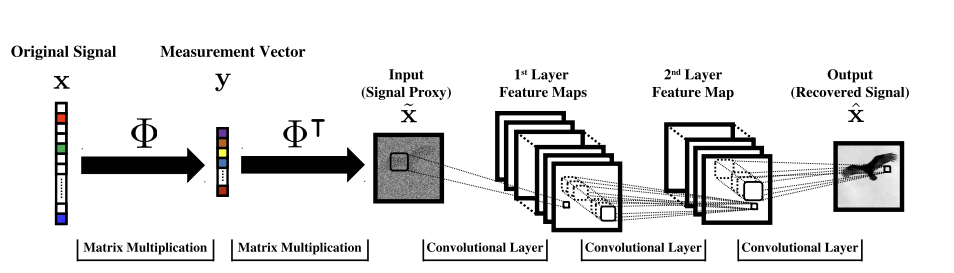
[Mousavi & Baraniuk, 2017]
[Ongie, Willet, et al, 2020]
Deep Learning in Inverse Problems
Option A: One-shot methods
Given enough training pairs \({(x_i,y_i)}\) train a network
\(f_\theta(y) = g_\theta(A^+y) \approx x\)
Option B: data-driven regularizer
\hat x = \arg\min_x \frac 12 \| y - A x \|^2_2 + {\color{Green}\hat R_\theta(x)}
[Lunz, Öktem, Schönlieb, 2020][Bora et al, 2017][Romano et al, 2017][Ye Tan, ..., Schönlieb, 2024]Deep Learning in Inverse Problems
\hat x = \arg\min_x \frac 12 \| y - A x \|^2_2 + R(x)
Proximal Gradient Descent: \( x^{k+1} = \text{prox}_R \left(x^k - \eta A^T(Ax^k-y)\right) \)
\hat{x}^{k+1} \leftarrow f_\theta \left( \hat{x}^k - \eta A^T(A \hat{x}^k - y)\right)
What if we don't know \(R(x)\), or \(\text{prox}_R\) ?
Train via:
f_{\hat{\theta}} \leftarrow \underset{\theta}{\min} \frac{1}{N} \displaystyle \sum_{i=1}^N \| x_i - \hat{x}_i^K(y_i)\|^2_2
Collect data:
\{(x_i,y_i)\}^N_{i=1}
pick a function class
f \in \mathcal H_\theta
Single Phase Quantitative Susceptibility Mapping
f_\theta
f_\theta
f_\theta
f_\theta
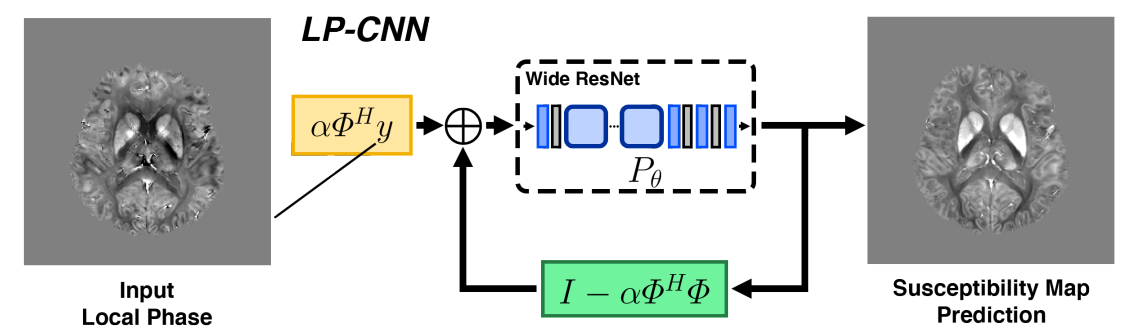
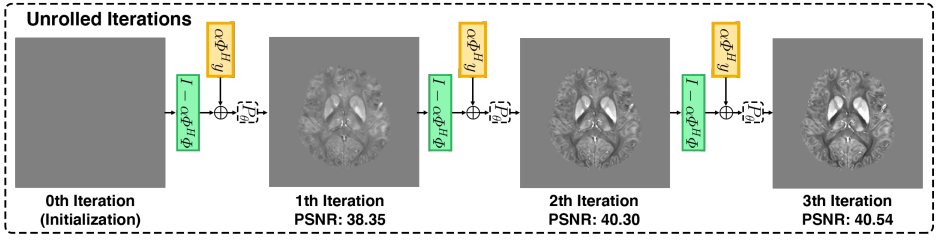
[Lai, Aggarwal, van Zijl, Li, Sulam, Learned Proximal Networks for Quantitative Susceptibility Mapping, MICCAI 2020]
(isotropic model)
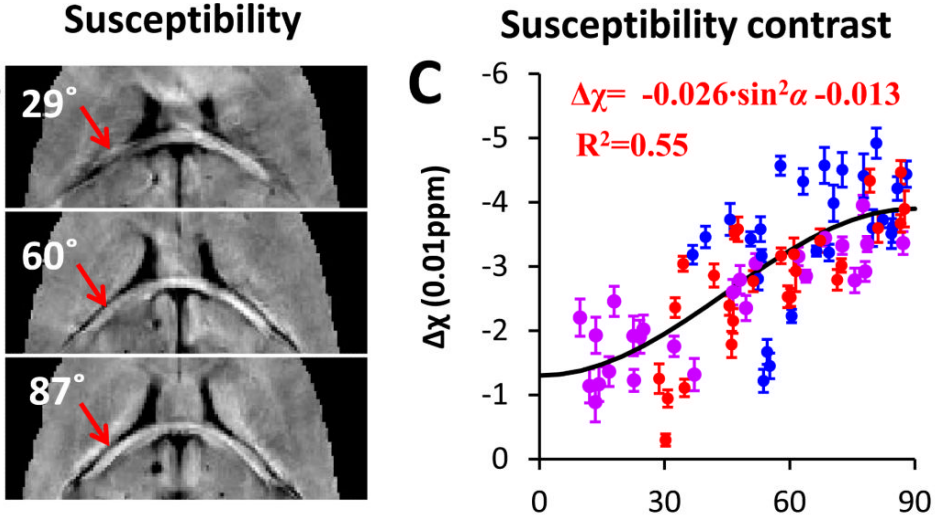
Single Phase Quantitative Susceptibility Mapping
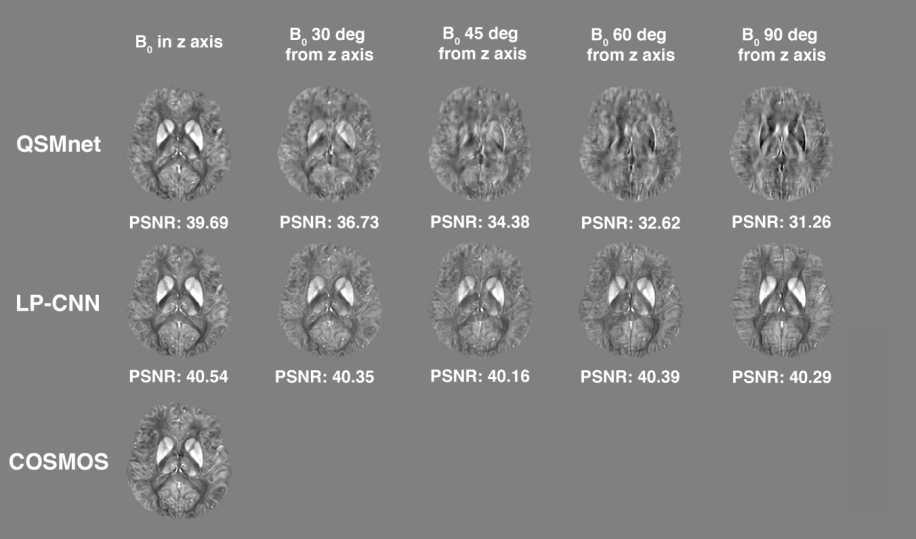
unseen angles during training
[Lai, Aggarwal, van Zijl, Li, Sulam, Learned Proximal Networks for Quantitative Susceptibility Mapping, MICCAI 2020]
(isotropic model)
Susceptibility Tensor Imaging
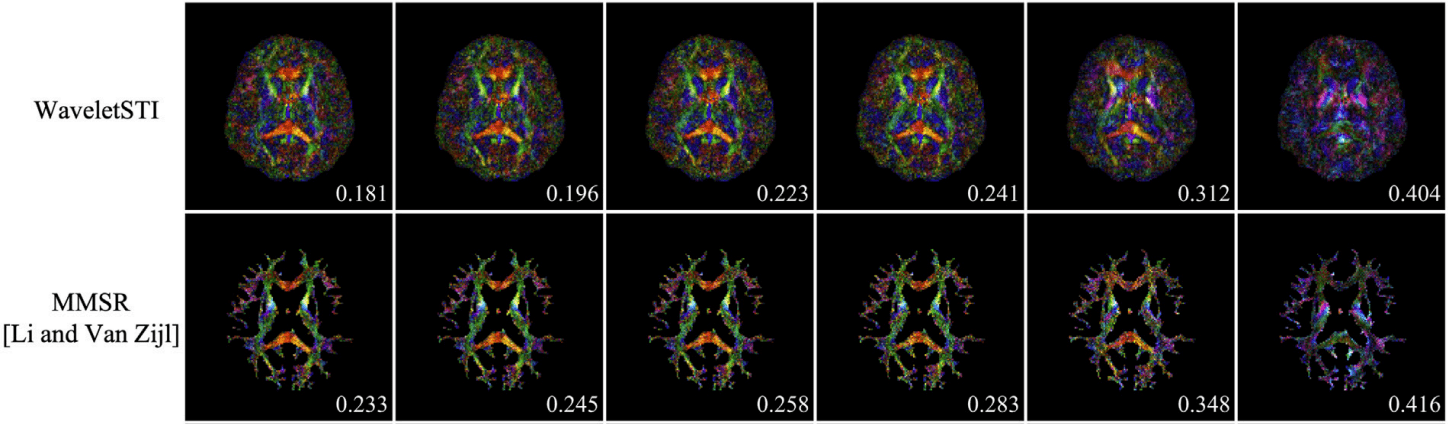
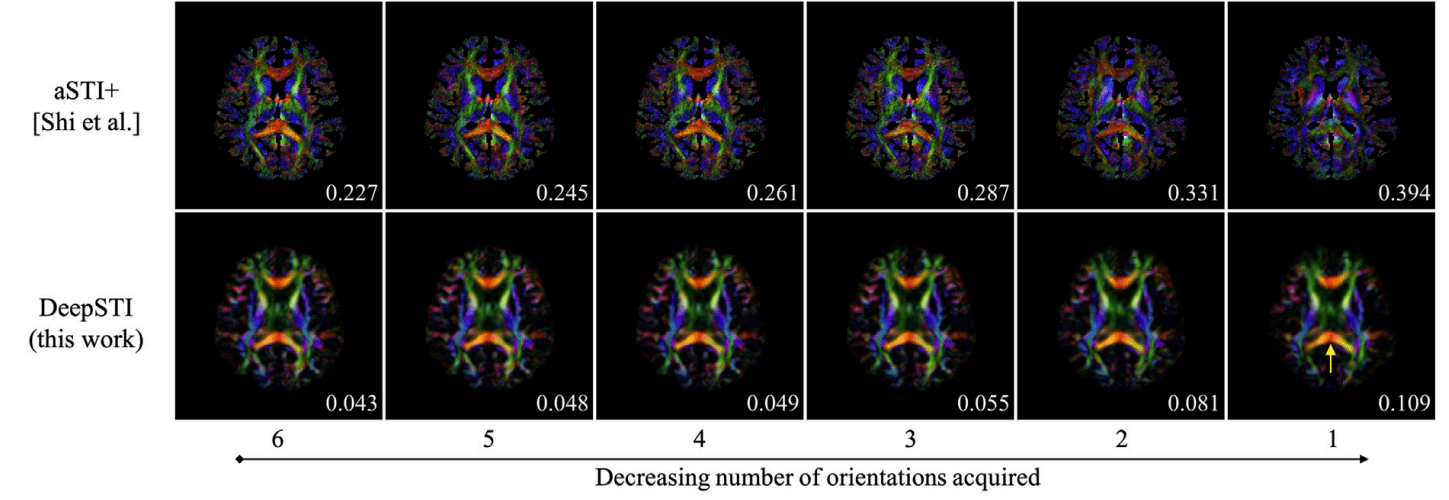
(anisotropic model)
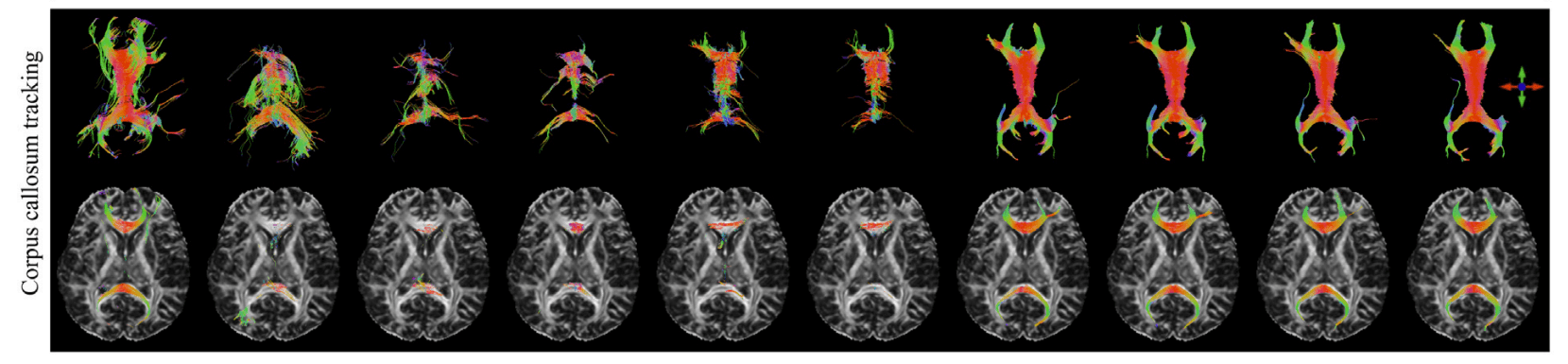
Susceptibility Tensor Imaging
What are these networks actually computing?
Deep Learning in Inverse Problems
Proximal Gradient Descent: \( x^{t+1} = \text{prox}_R \left(x^t - \eta A^T(Ax^t-y)\right) \)
\text{prox}_R \left( u \right) = \arg\min_x \frac 12 \|u - x\|_2^2 + R(x)
\text{prox}_R \left( u \right) = \texttt{MAP}(X|u), \qquad u = x + v
... a denoiser
\hat x = \arg\min_x \frac 12 \| y - A x \|^2_2 + R(x)
Deep Learning in Inverse Problems
any latest NN denoiser
[Venkatakrishnan et al., 2013; Zhang et al., 2017b; Meinhardt et al., 2017; Zhang et al., 2021; Kamilov et al., 2023b; Terris et al., 2023]
[Gilton, Ongie, Willett, 2019]
Proximal Gradient Descent: \( x^{t+1} = {\color{red}f_\theta} \left(x^t - \eta A^T(A(x^t)-y)\right) \)
\hat x = \arg\min_x \frac 12 \| y - A x \|^2_2 + R(x)
Question 1)
When will \(f_\theta(x)\) compute a \(\text{prox}_R(x)\) ? and for what \(R(x)\)?
Deep Learning in Inverse Problems
\(\mathcal H_\text{prox} = \{f : \text{prox}_R~ \text{for some }R\}\)
\(\mathcal H = \{f: \mathbb R^n \to \mathbb R^n\}\)
Question 1)
When will \(f_\theta(x)\) compute a \(\text{prox}_R(x)\) ? and for what \(R(x)\)?
Question 2)
Can we estimate the "correct" prox?
Deep Learning in Inverse Problems
\text{prox}_R : R(x) = -\log p_x(x)
\(\mathcal H_\text{prox} = \{f : \text{prox}_R~ \text{for some }R\}\)
\(\mathcal H = \{f: \mathbb R^n \to \mathbb R^n\}\)
\hat x = \arg\min_x \frac 12 \| y - A x \|^2_2 + R(x)
= \arg\min_x ~-\log p(y|x) - \log p(x)
= \arg\max_x~ p(x|y)
Interpretable Inverse Problems
Question 1)
When will \(f_\theta(x)\) compute a \(\text{prox}_R(x)\) ?
Theorem [Gibonval & Nikolova, 2020]
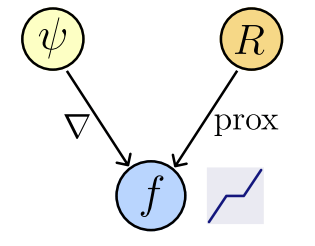
\( f(x) \in \text{prox}_R(x) ~\Leftrightarrow \exist ~ \text{convex l.s.c.}~ \psi: \mathbb R^n\to\mathbb R : f(x) \in \partial \psi(x)~\)
Interpretable Inverse Problems
Question 1)
When will \(f_\theta(x)\) compute a \(\text{prox}_R(x)\) ?
\(R(x)\) need not be convex!
Theorem [Gibonval & Nikolova, 2020]
Learned Proximal Networks
Take \(f_\theta(x) = \nabla \psi_\theta(x)\) for convex (and differentiable) \(\psi_\theta\)
\( f(x) \in \text{prox}_R(x) ~\Leftrightarrow \exist ~ \text{convex l.s.c.}~ \psi: \mathbb R^n\to\mathbb R : f(x) \in \partial \psi(x)~\)
Given \(f_\theta(x)\), we can compute \(R(x)\) via a LP
Interpretable Inverse Problems
If so, can you know for what \(R(x)\)?
Yes
R_\theta(x) = \langle {\color{red}\hat{f}^{-1}_\theta(x)},x\rangle - \frac 12 \|x\|^2_2 - \psi_\theta( {\color{red}\hat{f}^{-1}_\theta(x)} )
[Gibonval & Nikolova]
Easy! \[{\color{grey}y^* =} \arg\min_{y} \psi(y) - \langle y,x\rangle {\color{grey}= \hat{f}_\theta^{-1}(x)}\]
Interpretable Inverse Problems
Question 2)
Could we have \(R(x) = -\log p_x(x)\)?
(we don't know \(p_x\)!)
\text{Let } y = x+v , \quad ~ x\sim p_x, ~~v \sim \mathcal N(0,\sigma^2I)
f_\theta = \arg\min_{f_\theta:\text{prox}} \mathbb E_{x,y} \left[ {\ell (f_\theta(y),x)} \right]
\bullet ~~ {\ell (f_\theta(y),x)} = \|f_\theta(y) - x\|^2_2 ~~\implies~~ \mathbb E[x|y] \text{ (MMSE)}
\bullet ~~ {\ell (f_\theta(y),x)} = \|f_\theta(y) - x\|_1 ~~\implies~~ \texttt{median}(p_{x|y})
i.e. \(f_\theta(y) = \text{prox}_R(y) = \texttt{MAP}(x|y)\)
Which loss function?
Interpretable Inverse Problems
i.e. \(f_\theta(y) = \text{prox}_R(y) = \texttt{MAP}(x|y)\)
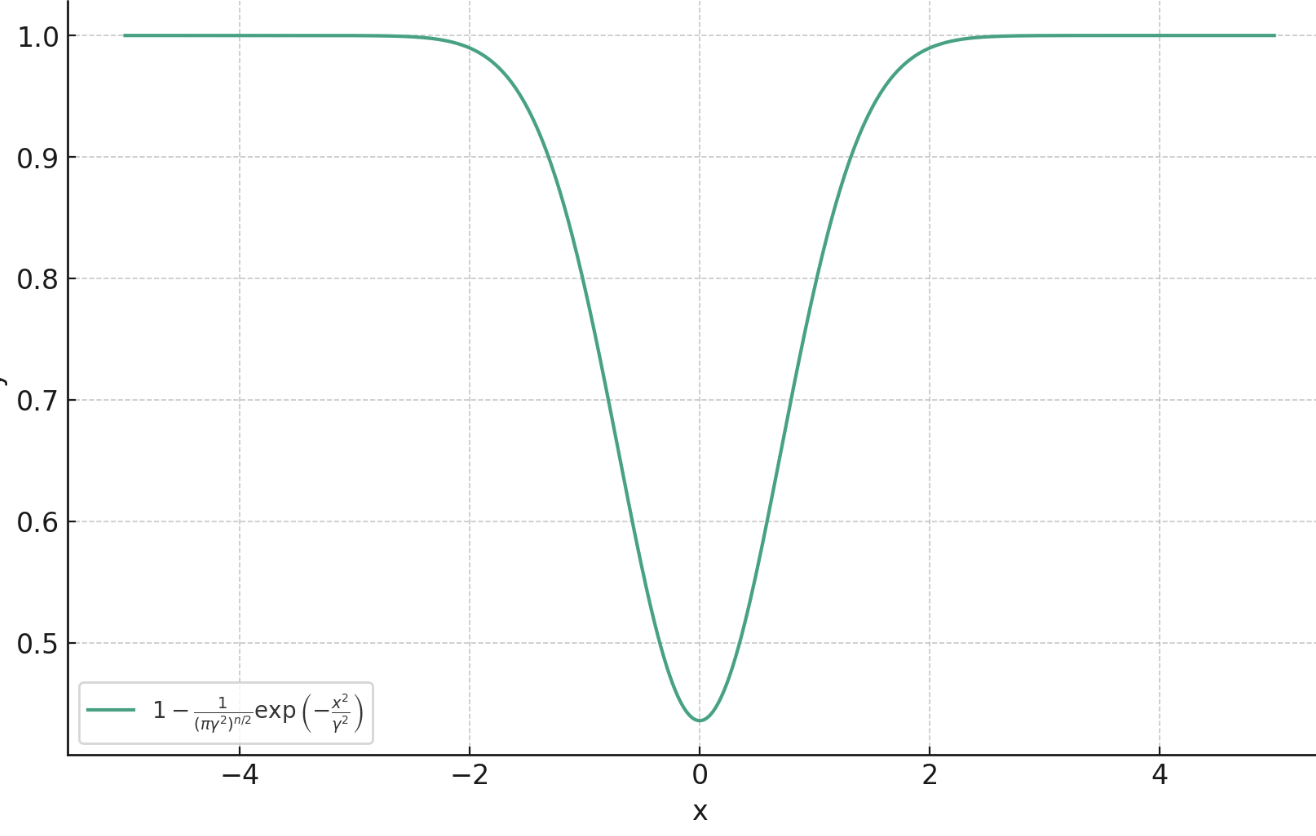
Theorem (informal)
\hat{f}^* = \arg\min_{f} \lim_{\gamma \searrow 0}~ \mathbb E_{x,y} \left[ \ell^\gamma_\text{PM}(f_\theta(y),x)\right]
\hat{f}^*(y) = \arg\max_c p_{x|y}(c) = \text{prox}_{-\sigma^2\log p_x}(y)
\ell^\gamma_\text{PM} (f_\theta(y),x) = 1- \frac{1}{(\pi\gamma^2)^{n/2}} \exp\left( -\frac{\|f(y)-x\|_2^2}{\gamma} \right)
Proximal Matching Loss
\(\gamma\)
Question 2)
Could we have \(R(x) = -\log p_x(x)\)?
(we don't know \(p_x\)!)
Learned Proximal Networks
\text{Sample } y = x+v,~ \text{ with } x \sim \text{Laplace}(0,1) \text{ and } v \sim \mathcal N(0,\sigma^2)
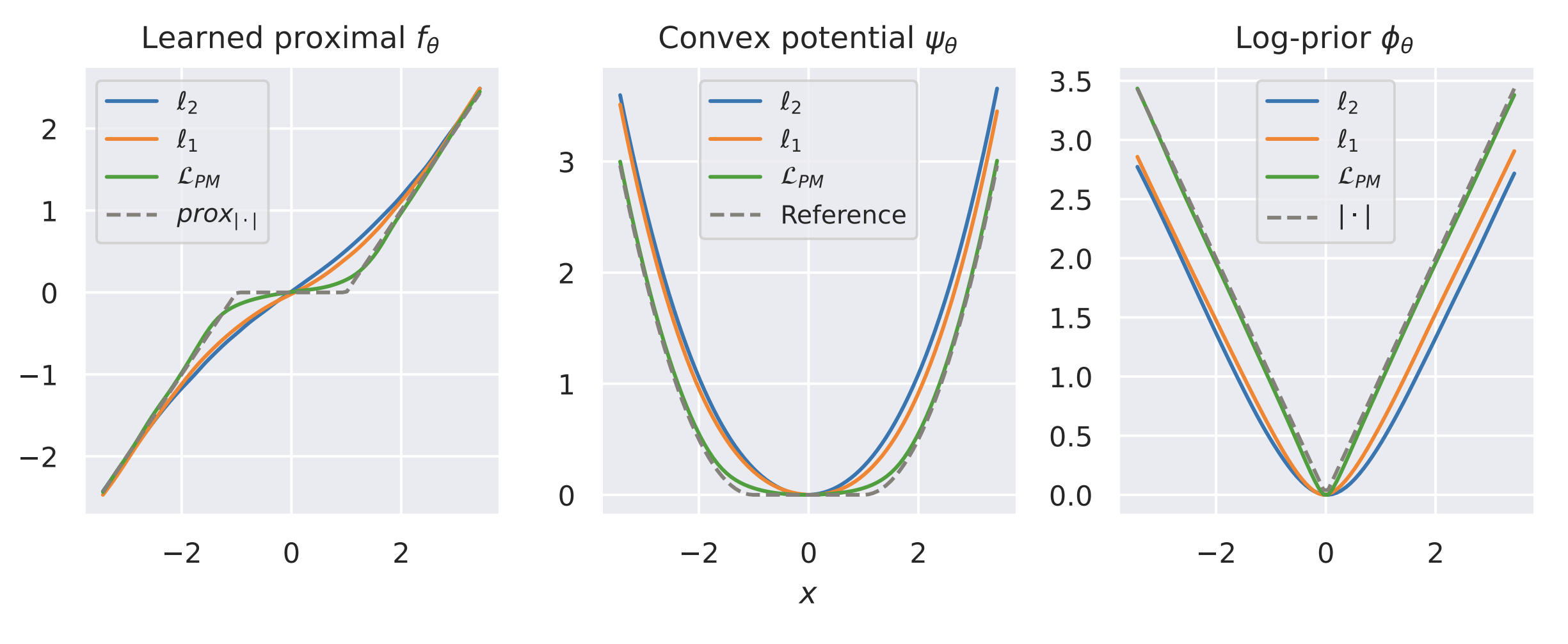
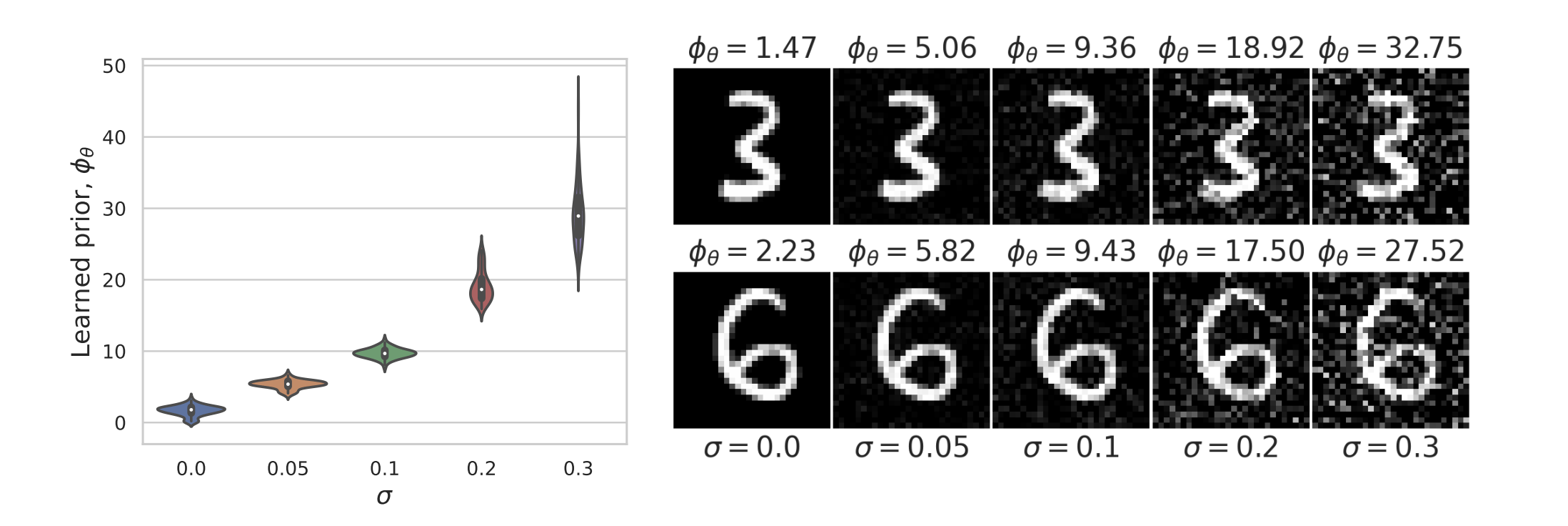
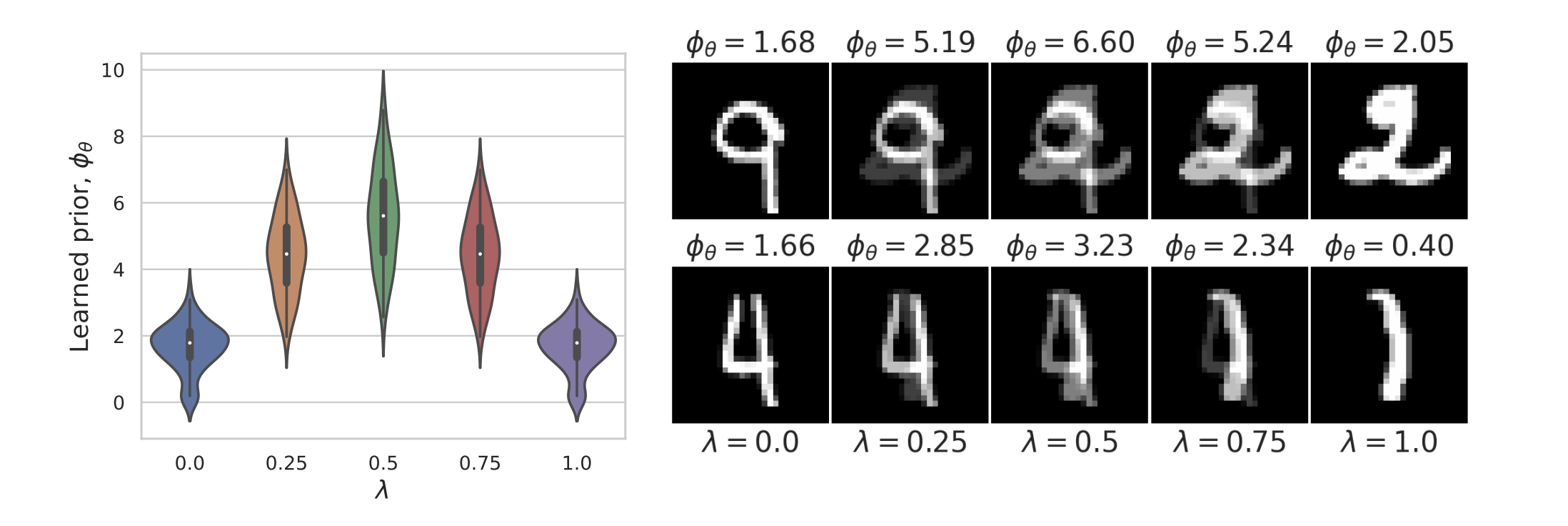
Learned Proximal Networks
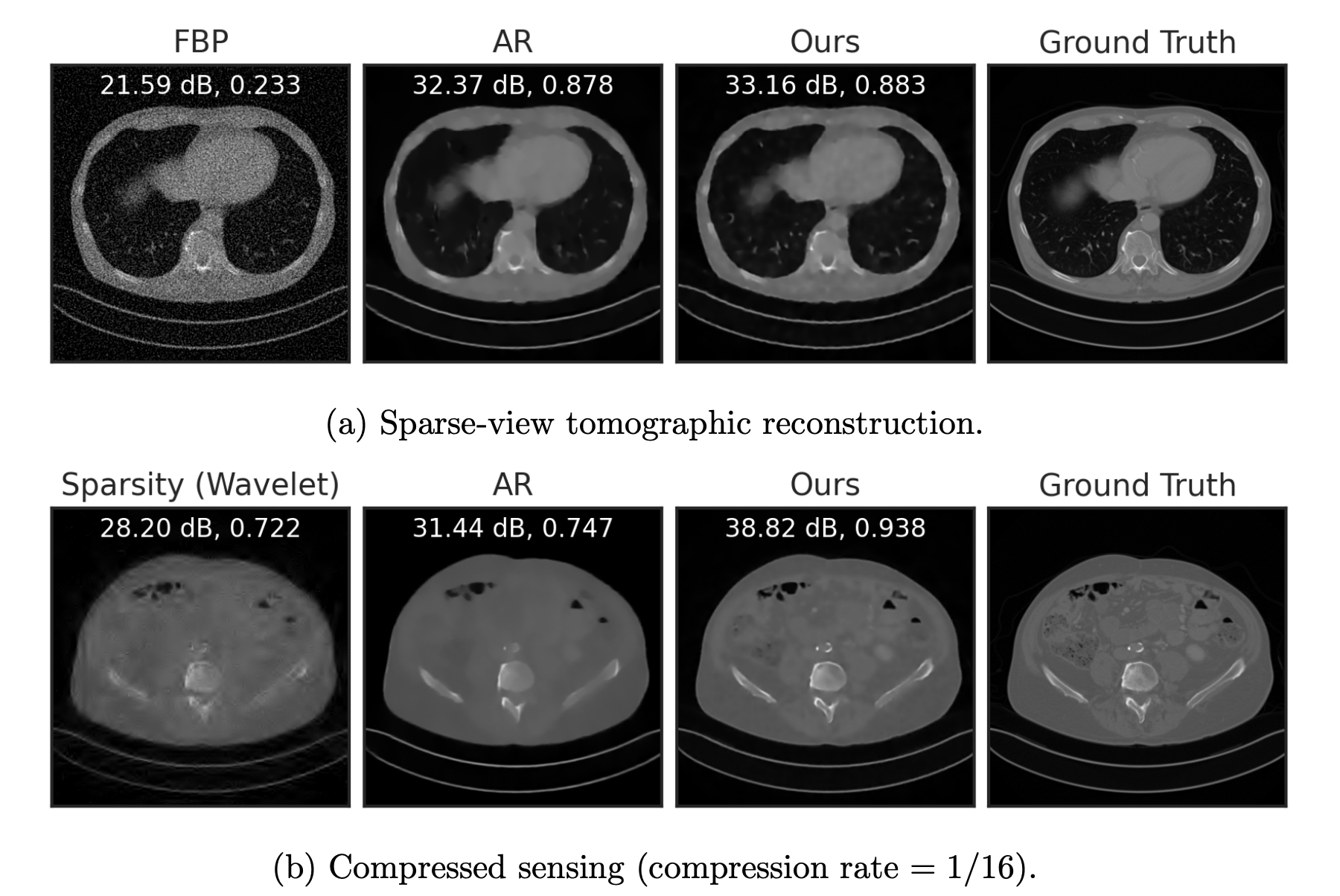
Fang, Buchanan & S. What's in a Prior? Learned Proximal Networks for Inverse Problems. ICLR 2024.
Learned Proximal Networks
+ Convergence guarantees
What did my model learn?
PART I
Inverse Problems
PART II
Image Classification
Two vignettes on medical imaging
Interpretable Image Classification
{f}\huge(
{\huge)} = \text{\texttt{sick}}
What parts of the image are important for this prediction?
What are the subsets of the input so that
{f}(x_C) \approx {f}(x) ?
C \subseteq [d]
-
Sensitivity or Gradient-based perturbations
-
Shapley coefficients
-
Variational formulations
-
Counterfactual explanations
LIME [Ribeiro et al, '16], CAM [Zhou et al, '16], Grad-CAM [Selvaraju et al, '17]
Shap [Lundberg & Lee, '17], ...
RDE [Macdonald et al, '19], ...
[Sani et al, 2020] [Singla et al '19],..
Interpretability
efficiency
nullity
symmetry
exponential complexity
Lloyd S Shapley. A value for n-person games. Contributions to the Theory of Games, 2(28):307–317, 1953.
Let be an -person cooperative game with characteristic function
G = ([n],f)
n
f : \mathcal P([n]) \mapsto \mathbb R
How important is each player for the outcome of the game?
\displaystyle \phi_i = \sum_{S_j\subseteq [n]\setminus \{i\} } w_{S_j} \left[ f(S_j\cup \{i\}) - f(S_j) \right]
marginal contribution of player i with coalition S
Shapley values
\displaystyle \phi_i = \sum_{S_j\subseteq [n]\setminus \{i\}} w_j ~ \mathbb ~~ \left[ f(\tilde X_{S_j\cup \{i\}}) - f(\tilde X_{S_j}) \right]
Shap-Explanations
X \in \mathcal X \subset \mathbb R^n
Y\in \mathcal Y = \{0,1\}
inputs
responses
f:\mathcal X \to \mathcal Y
predictor
How important is feature \(x_i\) for \(f(x)\)?
x_{S_j}
\tilde{X}_{S_j}:
X_{S_j^c}
\(X_{S_j^c}\sim \mathcal D_{X_{S_j}={x_{S_j}}}\)
Scott Lundberg and Su-In Lee. A Unified Approach to Interpreting Model Predictions, NeurIPS , 2017
\displaystyle \phi_i = \sum_{S_j\subseteq [n]\setminus \{i\}} w_j ~ \mathbb E \left[ f(\tilde X_{S_j\cup \{i\}}) - f(\tilde X_{S_j}) \right]
Shap-Explanations
X \in \mathcal X \subset \mathbb R^n
Y\in \mathcal Y = \{0,1\}
inputs
responses
How important is feature \(x_i\) for \(f(x)\)?
x_{S_j}
\tilde{X}_{S_j}:
X_{S_j^c}
f:\mathcal X \to \mathcal Y
predictor
\(X_{S_j^c}\sim \mathcal D_{X_{S_j}={x_{S_j}}}\)
Scott Lundberg and Su-In Lee. A Unified Approach to Interpreting Model Predictions, NeurIPS , 2017
Shap-Explanations
Question 1)
Can we resolve the computational bottleneck (and when) ?
Question 2)
What do these coefficients mean, really?
Question 3)
How to go beyond input-features explanations?
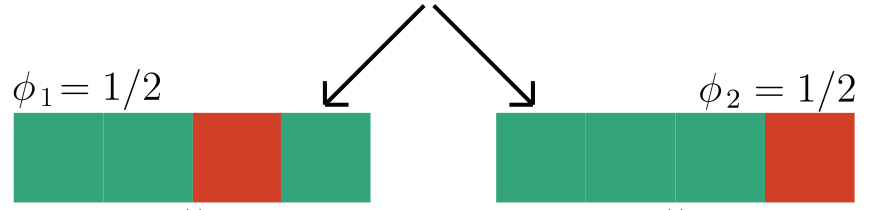
We focus on data with certain structure:
f\huge(
{\huge)} = 0
{f}\huge(
{\huge)} = 1
{f}\huge(
{\huge)} = 0
Example:
f(x) = 1
if contains a sick cell
x
Hierarchical Shap (h-Shap)
\text{\textbf{Assumption 1:}}~ f(x) = 1 \Leftrightarrow \exist~ i: f(\tilde X_i) = 1
Question 1) Can we resolve the computational bottleneck (and when) ?
Theorem (informal)
-
hierarchical Shap runs in linear time
-
Under A1, h-Shap \(\to\) Shapley
\mathcal O(2^\gamma k \log n)
[Teneggi, Luster & S., IEEE TPAMI, 2022]
We focus on data with certain structure:
f\huge(
{\huge)} = 0
{f}\huge(
{\huge)} = 1
{f}\huge(
{\huge)} = 0
Example:
f(x) = 1
if contains a sick cell
x
Hierarchical Shap (h-Shap)
\text{\textbf{Assumption 1:}}~ f(x) = 1 \Leftrightarrow \exist~ i: f(\tilde X_i) = 1
Question 1) Can we resolve the computational bottleneck (and when) ?
Theorem (informal)
-
hierarchical Shap runs in linear time
-
Under A1, h-Shap \(\to\) Shapley
\mathcal O(2^\gamma k \log n)
[Teneggi, Luster & S., IEEE TPAMI, 2022]
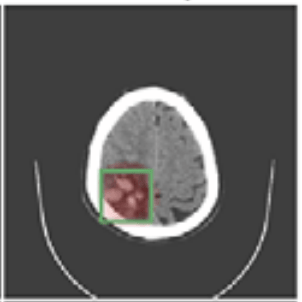
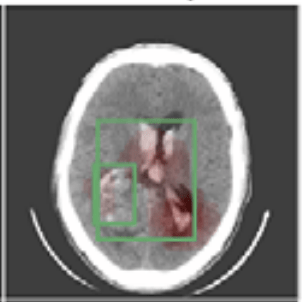
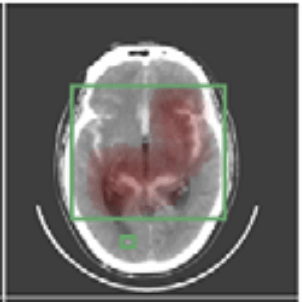
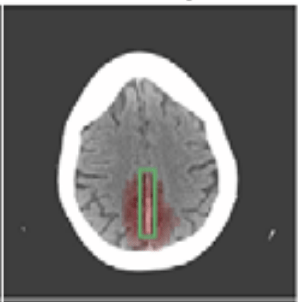
Question 2) What do these coefficients mean, really?
Precise notions of importance
Formal Feature Importance
H_{0,S}:~ X_S \perp\!\!\!\perp Y | X_{[n]\setminus S}
[Candes et al, 2018]
Question 2) What do these coefficients mean, really?
Precise notions of importance
XRT: eXplanation Randomization Test
returns a \(\hat{p}_{i,S}\) for the test above
\text{reject} ~\Rightarrow~ i=2 \text{: important}
H^0_{i=2,S=\{1,3,4\}}
i=1
i=2
i=3
i=4
How do we test?
\text{For any } S \subseteq [n]\setminus \{{\color{Red}i}\}, \text{ and a sample } x\sim \mathcal p_X
H^0_{{\color{red}i},S}:~ (f(\tilde X_{S\cup \{{\color{red}i}\}}) ) \overset{d}{=} (f(\tilde X_{S}) )
Local Feature Importance
Precise notions of importance
Local Feature Importance
\text{For any } S \subseteq [n]\setminus \{{\color{Red}i}\}, \text{ and a sample } x\sim \mathcal D_X
H^0_{{\color{red}i},S}:~ (f(\tilde X_{S\cup \{{\color{red}i}\}}) ) \overset{d}{=} (f(\tilde X_{S}) )
\gamma_{i,S}
\displaystyle \phi_{\color{red}i}(x) = \sum_{S\subseteq [n]\setminus \{{\color{red}i}\}} w_{S} ~ \mathbb E \left[ f(\tilde X_{S\cup \{{\color{red}i}\}}) - f(\tilde X_S) \right]
Given the Shapley coefficient of any feature
Then
p_{i,S}
and the (expected) p-value obtained for , i.e. ,
H^0_{i,S}
Theorem:
p_{i,S} \leq 1 - \gamma_{i,S}.
i\in[n],
Teneggi, Bharti, Romano, and S. "SHAP-XRT: The Shapley Value Meets Conditional Independence Testing." TMLR (2023).
Question 3)
How to go beyond input-features explanations?
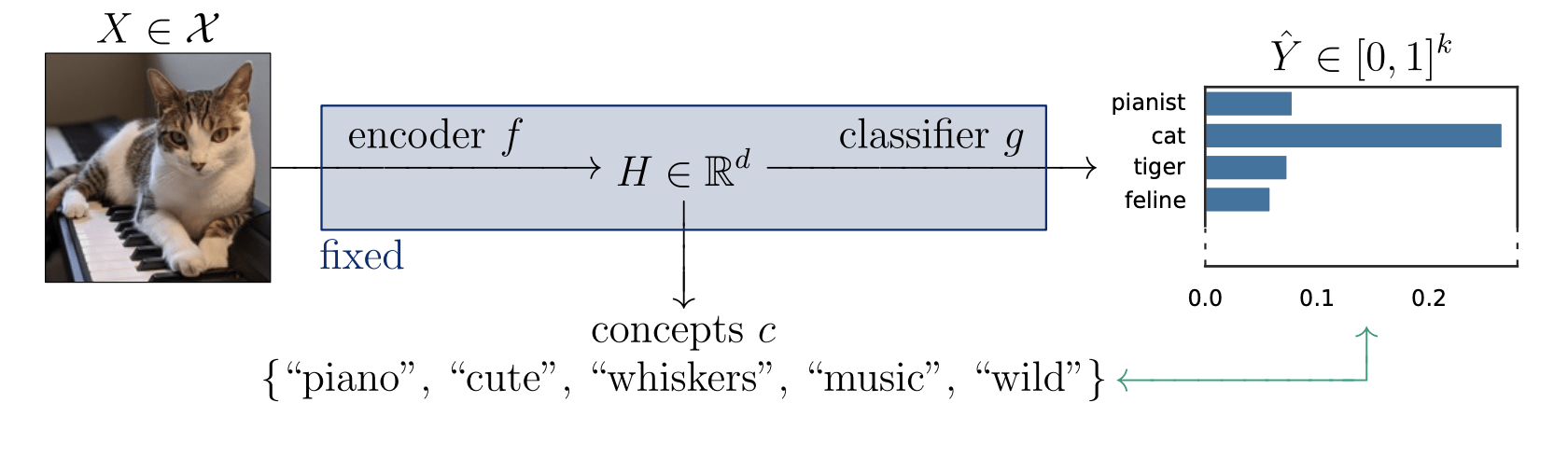
Is the piano important for \(\hat Y = \text{cat}\) given that there is a cute mammal?
Testing Semantic Importance
Question 3) How to go beyond input-features explanations?
Precise notions of semantic importance
semantics \(Z = c^TH\)
embeddings \(H = f(X)\)
predictions \(\hat{Y} = g(H)\)
Concept Bottleneck Models (CBM)
[Koh et al '20, Yang et al '23, Yuan et al '22, Yuksekgonul '22 ]
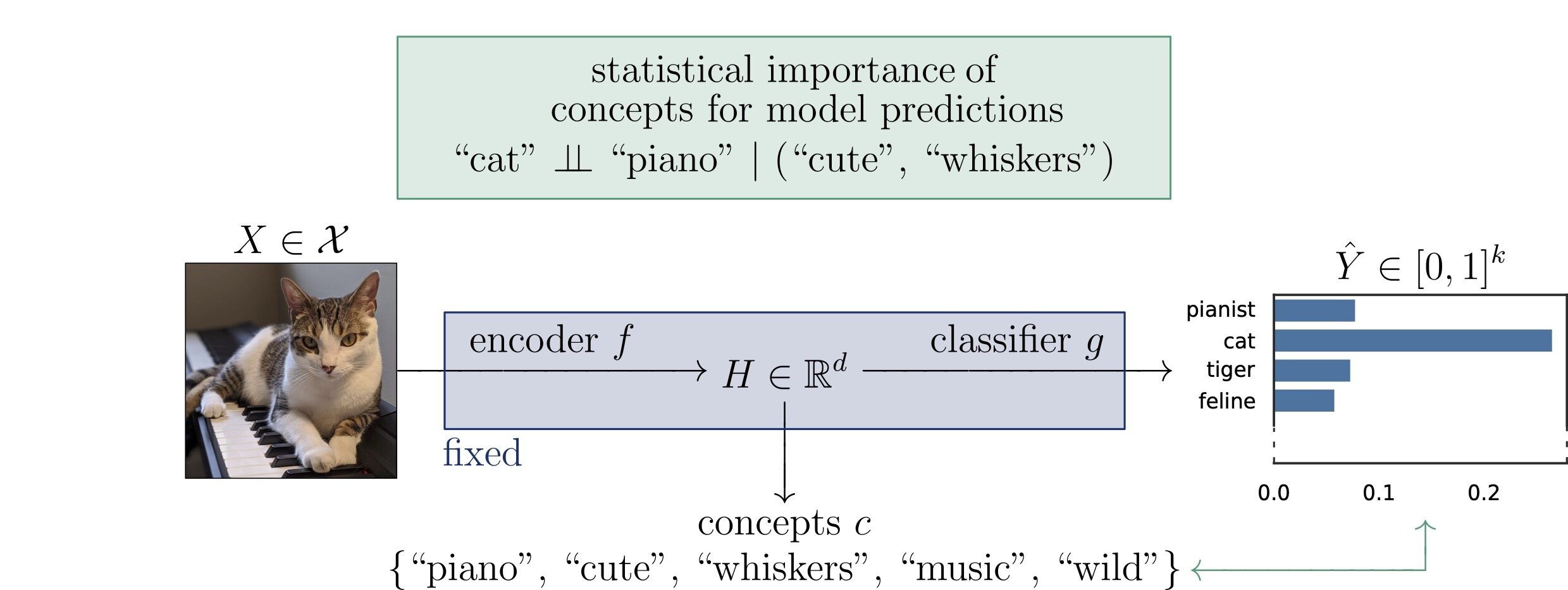
Precise notions of semantic importance
semantic XRT
\[H^{j,S}_0:~g(\widetilde{H}_{S \cup \{j\}}) \overset{d}{=} g(\widetilde{H}_S),\quad\widetilde{H}_C \sim P_{H | Z_C = z_C}\]
"The classifier (its distribution) does not change if we condition
on concepts \(S\) vs on concepts \(S\cup\{j\} \)"
semantics \(Z = c^TH\)
embeddings \(H = f(X)\)
predictions \(\hat{Y} = g(H)\)
Precise notions of semantic importance
semantic XRT
\[H^{j,S}_0:~g(\widetilde{H}_{S \cup \{j\}}) \overset{d}{=} g(\widetilde{H}_S),\quad\widetilde{H}_C \sim P_{H | Z_C = z_C}\]
"The classifier (its distribution) does not change if we condition
on concepts \(S\) vs on concepts \(S\cup\{j\} \)"
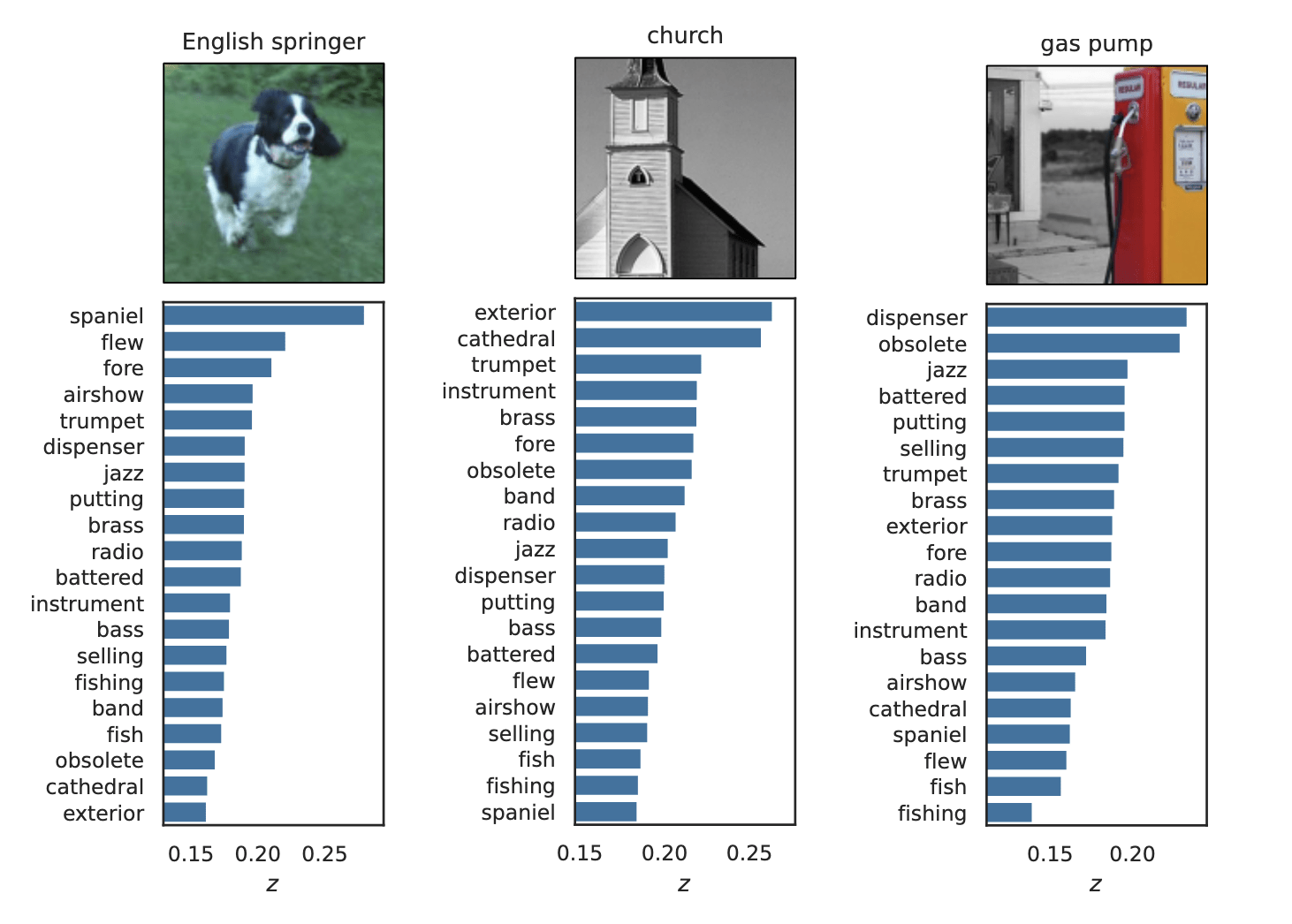
\(\hat{Y}_\text{gas pump}\)
\(Z_S\cup Z_{j}\)
\(Z_{S}\)
Precise notions of semantic importance
semantic XRT
\[H^{j,S}_0:~g(\widetilde{H}_{S \cup \{j\}}) \overset{d}{=} g(\widetilde{H}_S),\quad\widetilde{H}_C \sim P_{H | Z_C = z_C}\]
"The classifier (its distribution) does not change if we condition
on concepts \(S\) vs on concepts \(S\cup\{j\} \)"
\(\hat{Y}_\text{gas pump}\)
\(\hat{Y}_\text{gas pump}\)
\(Z_S\cup Z_{j}\)
\(Z_{S}\)
\(Z_S\cup Z_{j}\)
\(Z_{S}\)
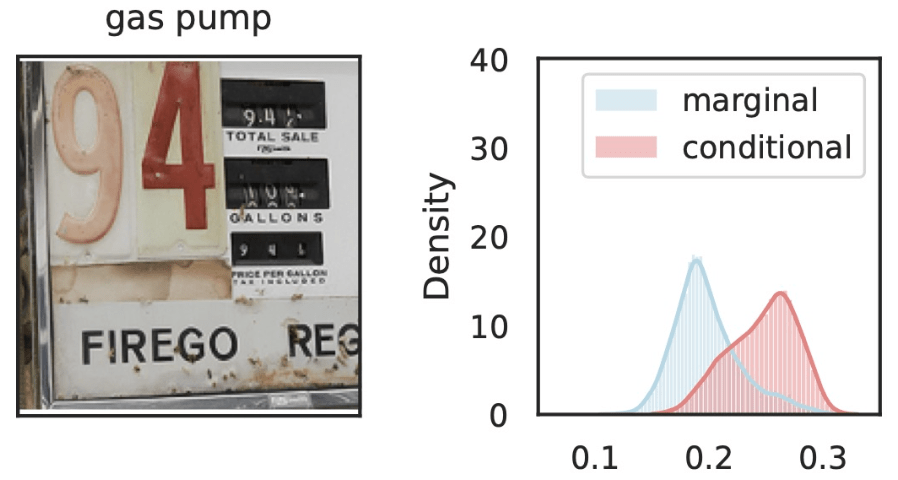
Precise notions of semantic importance
semantic XRT
\[H^{j,S}_0:~g(\widetilde{H}_{S \cup \{j\}}) \overset{d}{=} g(\widetilde{H}_S),\quad\widetilde{H}_C \sim P_{H | Z_C = z_C}\]
Testing by Betting
- Instantiate a wealth process
\(K_0 = 1\)
\(K_t = K_{t-1}(1+\kappa_t v_t)\)
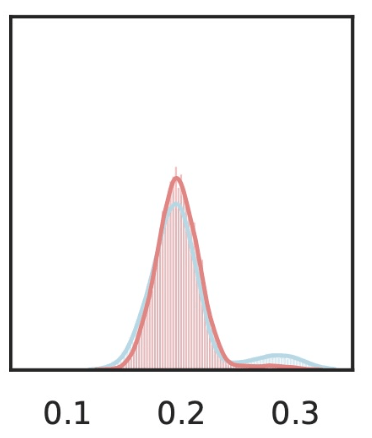
- Reject \(H_0\) when \(K_t \geq 1/\alpha\)
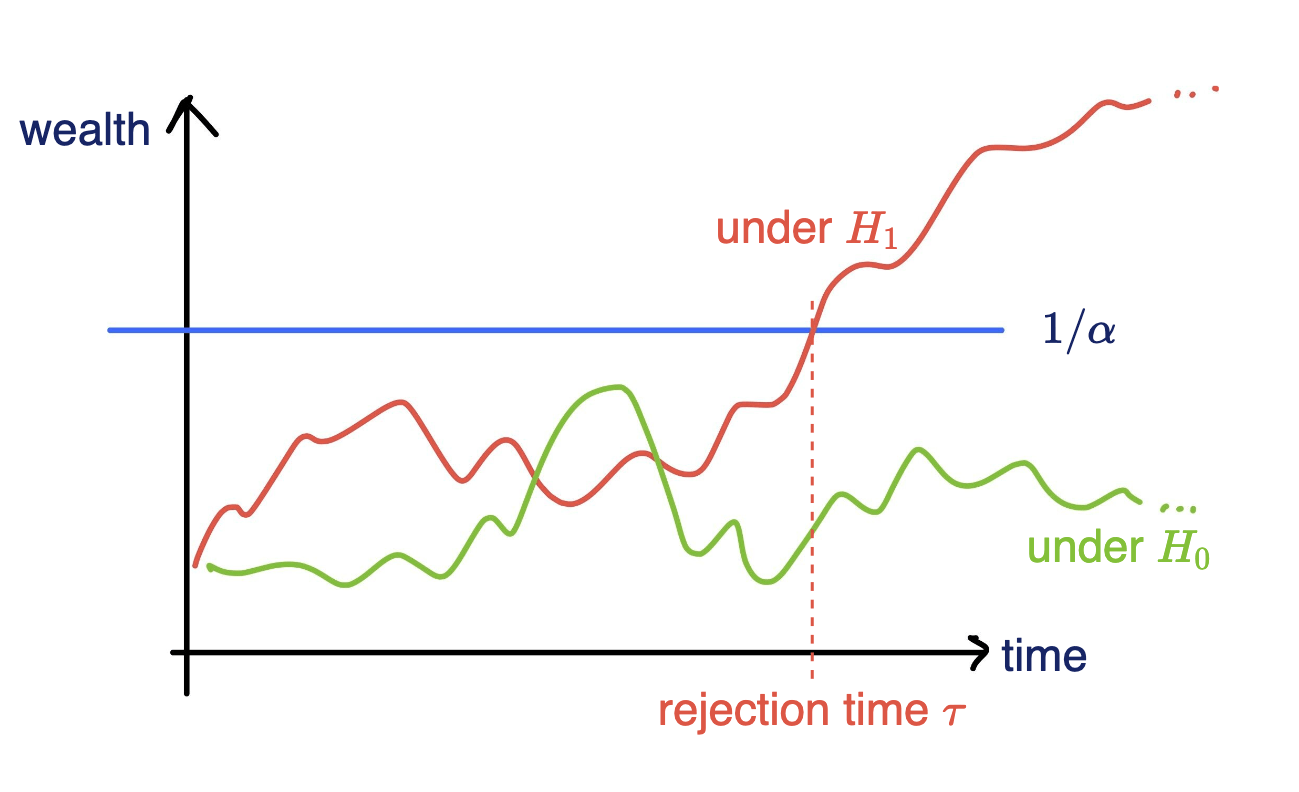
[Shaer et al. 2023, Shekhar and Ramdas 2023 ]
Precise notions of semantic importance
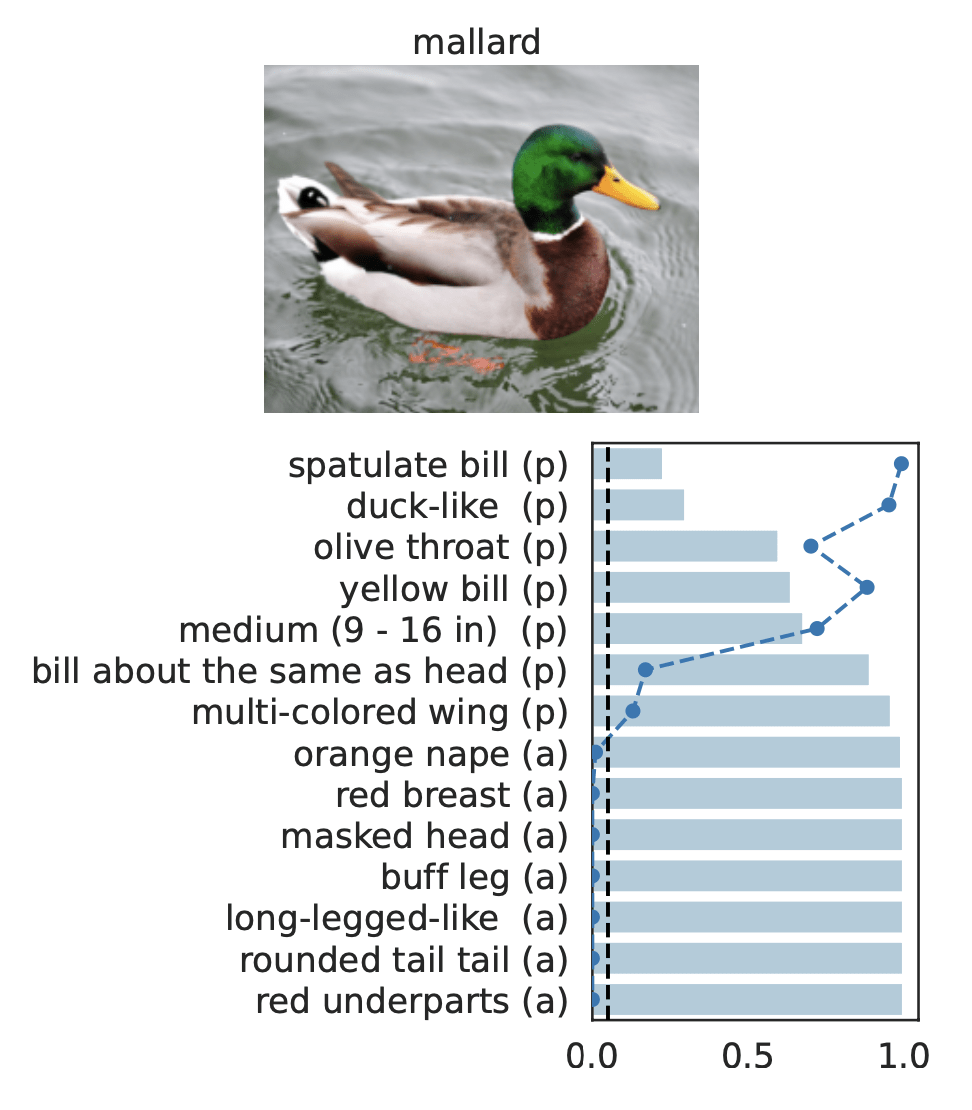
Important Semantic Concepts
(Reject \(H_0\))
Unimportant Semantic Concepts
(fail to reject \(H_0\))
- Type 1 error control
- False discovery rate control
rejection rate
rejection time
Precise notions of semantic importance
-
Exciting open problems to making AI tools safe, trustworthy and interpretable
-
Importance in clear definitions and guarantees
Concluding Remarks
* Fang, Z., Buchanan, S., & J.S. (2023). What's in a Prior? Learned Proximal Networks for Inverse Problems. International Conference on Learning Representations. * Teneggi, J., Luster, A., & J.S. (2022). Fast hierarchical games for image explanations. IEEE Transactions on Pattern Analysis and Machine Intelligence. * Teneggi, J., B. Bharti, Y. Romano, and J.S. (2023) SHAP-XRT: The Shapley Value Meets Conditional Independence Testing. Transactions on Machine Learning Research. * Teneggi, J. and J.S. I Bet You Did Not Mean That: Testing Semantic Importance via Betting. NeurIPS 2024 (to appear).
Interpretability
Fairness
Uncertainty Quantification
Inverse Problems
(some) Challenges in Biomedical Data Science
Interpretability
Fairness
Uncertainty Quantification
Inverse Problems
(some) Challenges in Biomedical Data Science
Fairness in Data Science
Is the model fair?
\text{TPR}_{A} = \mathbb P [\hat Y = 1 | Y = 0, {A}]
Pneumonia
Clear
95% accurate
\Delta_{\text{TPR}} = {\Large|} \mathbb P [\hat Y = 1 | Y = 0, {\color{blue}A=0}] - \mathbb P [\hat Y = 1 | Y = 0, {\color{blue}A=1}] {\Large|}
Fairness in Data Science
Does your model achieve a \(\Delta_{\text{TPR}}\) of at most (say) 6% ?
Fairness in Data Science
Pneumonia
Clear
95% accurate
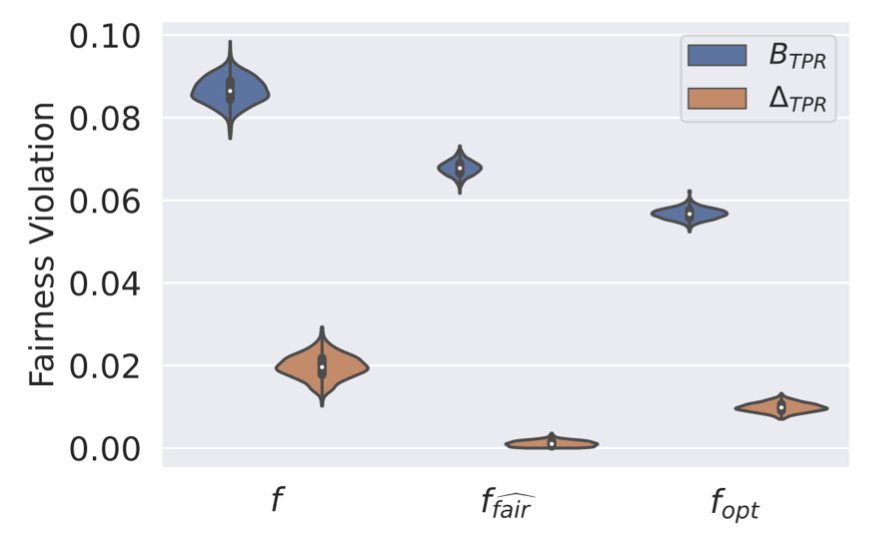
Tight upper bounds to fairness violations
(optimally) Actionable
Maximum TPR
discrepancy
True TPR
discrepancy
Bharti, B., Yi, P., & Sulam, J. (2023). Estimating and Controlling for Equalized Odds via Sensitive Attribute Predictors NeurIPS 2023Fairness in Data Science
Pneumonia
Clear
95% accurate
How to quantify and report uncertainty?
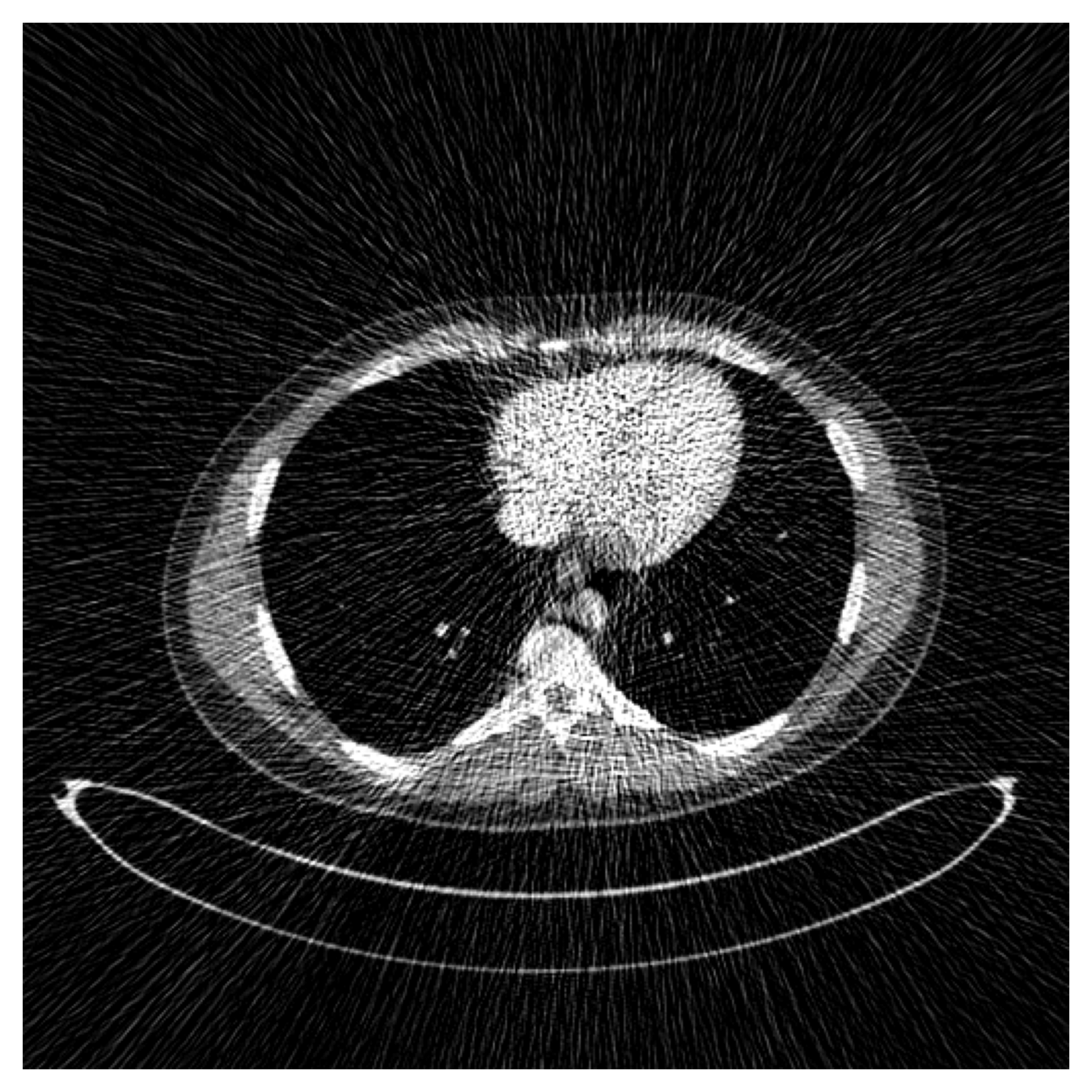
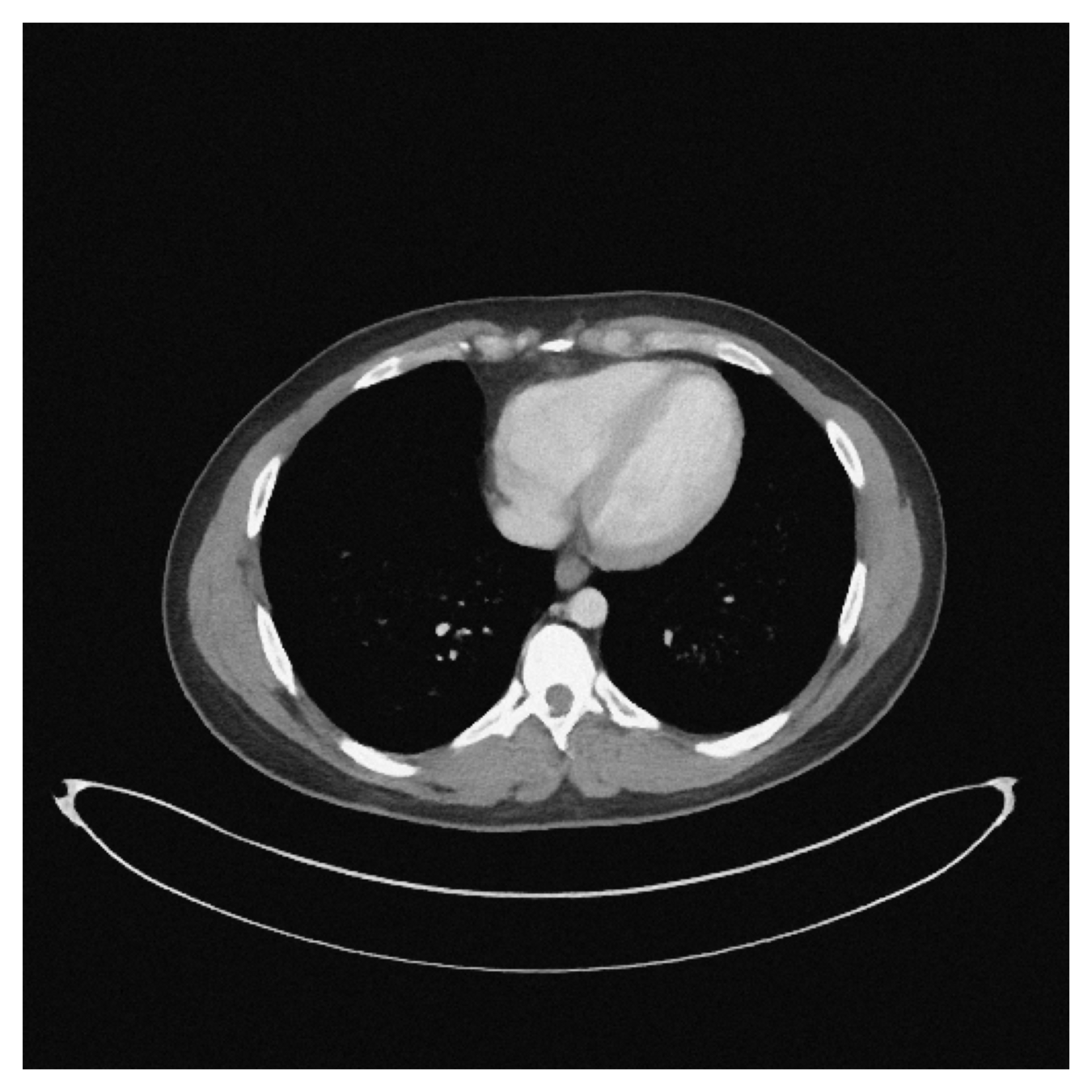
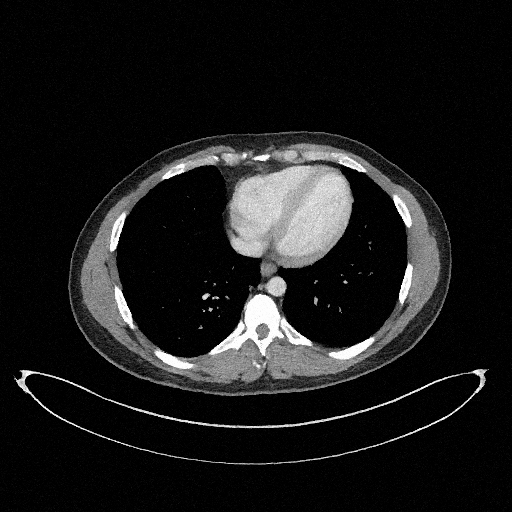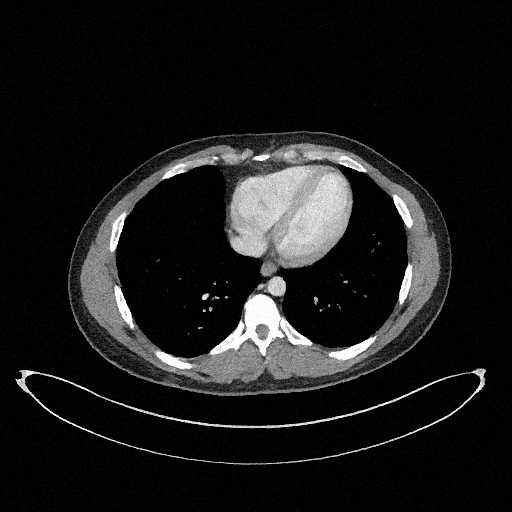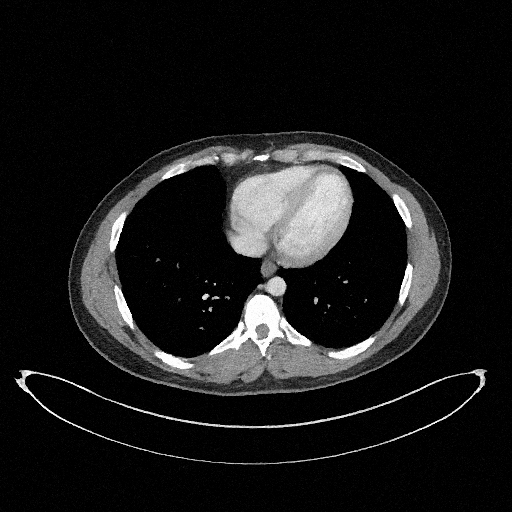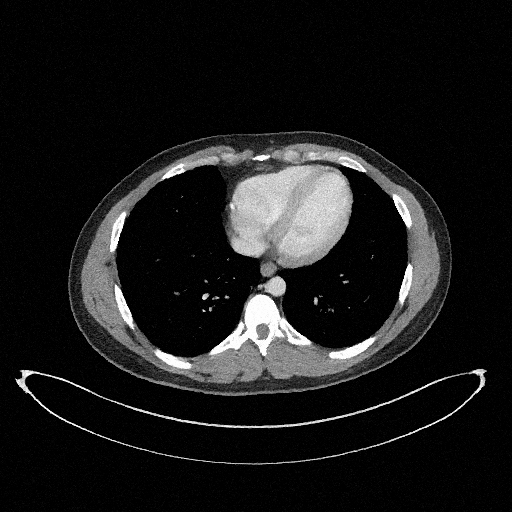
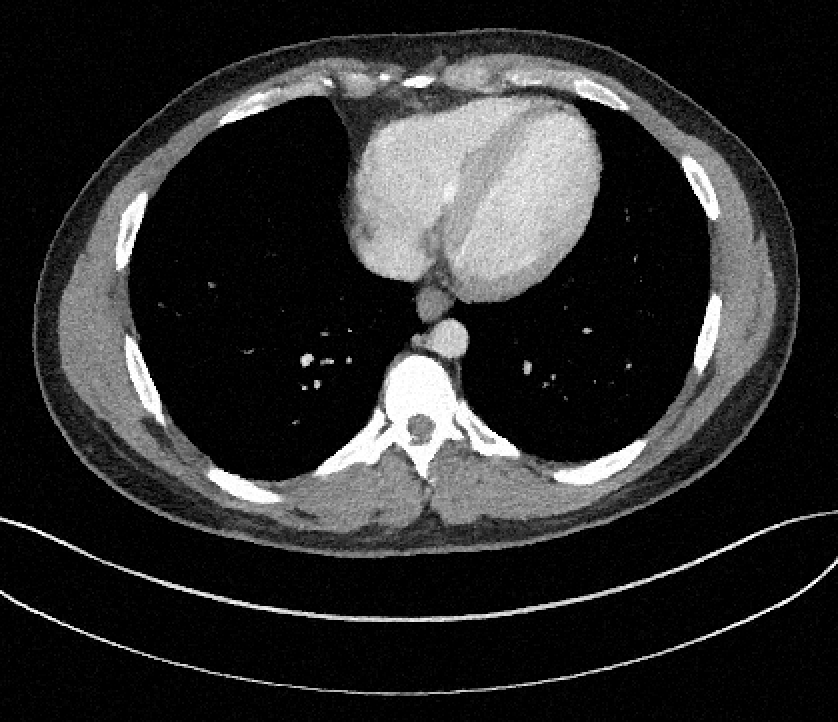
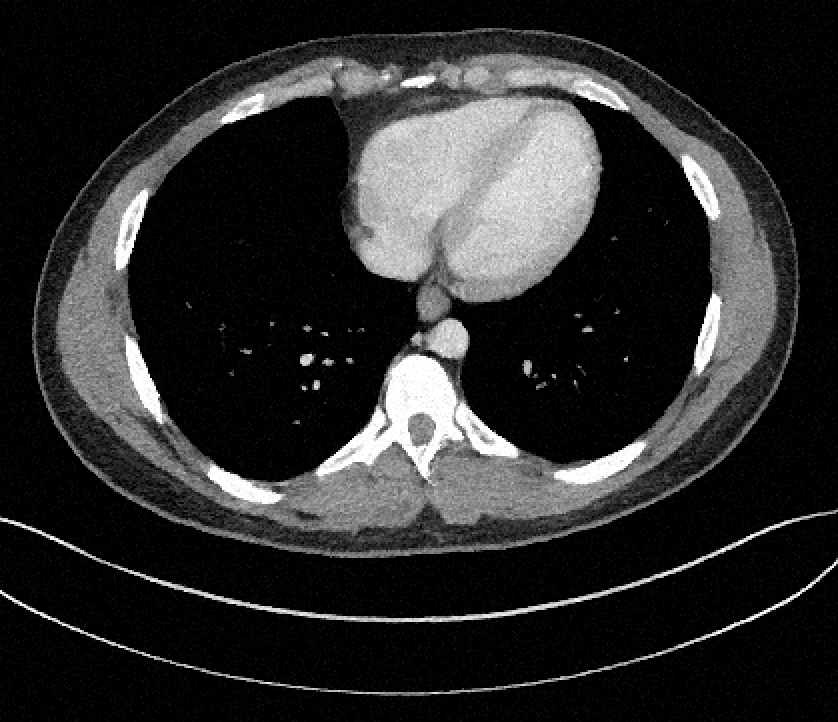
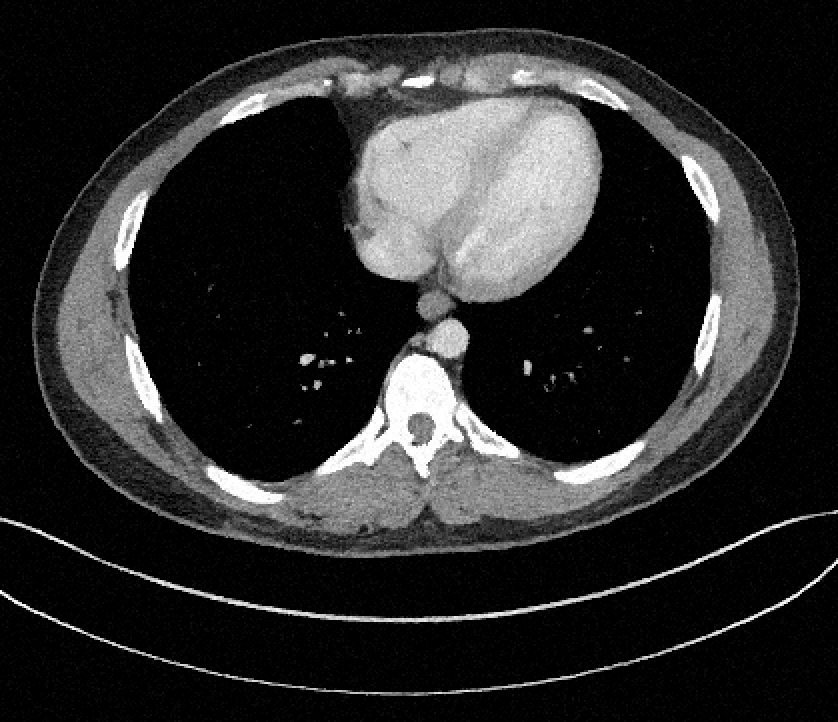
Filtered Back Projection
Deep ConvNet Model
Diffusion Model
Uncertainty Quantification
For an observation \(y\)
\[y = x + \epsilon,~\epsilon \sim \mathcal{N}(0, \sigma^2\mathbb{I})\]
reconstruct \(x\) with
\[\hat{x} = F(y) \sim \mathcal{Q}_y \approx p(x \mid y)\]
Uncertainty Quantification
\(x\)
\(y\)
\(F(y)\)
Lemma
\(\mathcal I(y)\) provides entrywise coverage for pixel \(j\), i.e.
\[\mathbb{P}\left[\text{next sample}_j \in \mathcal{I}(y)_j\right] \geq 1 - \alpha\]
If \[\mathcal{I}(y)_j = \left[ \frac{\lfloor(m+1)Q_{\alpha/2}(y_j)\rfloor}{m} , \frac{\lceil(m+1)Q_{1-\alpha/2}(y_j)\rceil}{m}\right]\]
Uncertainty Quantification
\(0\)
\(1\)
low: \( l(y) \)
\(\mathcal{I}(y)\)
up: \( u(y) \)
(distribution free)
\(x\)
\(y\)
lower
upper
intervals
\(|\mathcal I(y)_j|\)
Uncertainty Quantification
\(0\)
\(1\)
Risk Controlling Prediction Sets
ground-truth is
contained
\(\mathcal{I}(y_j)\)
\(x_j\)
Procedure For pixel \(j\)
\[\mathcal{I}_{\lambda}(y)_j = [\text{lower} - \lambda, \text{upper} + \lambda]\]
choose
\[\hat{\lambda} = \inf\{\lambda \in \mathbb{R}:~\forall \lambda' \geq \lambda,~\text{risk}(\lambda') \leq \epsilon\}\]
ground-truth is
contained
\(0\)
\(1\)
\(\mathcal{I}(y_j)\)
\(\lambda\)
\(x_j\)
Risk Controlling Prediction Sets
Definition For risk level \(\epsilon\), failure probability \(\delta\), \(\mathcal{I}(y_j) \) is a RCPS if
\[\mathbb{P}\left[\mathbb{E}\left[\text{fraction of pixels not in intervals}\right] \leq \epsilon\right] \geq 1 - \delta\]
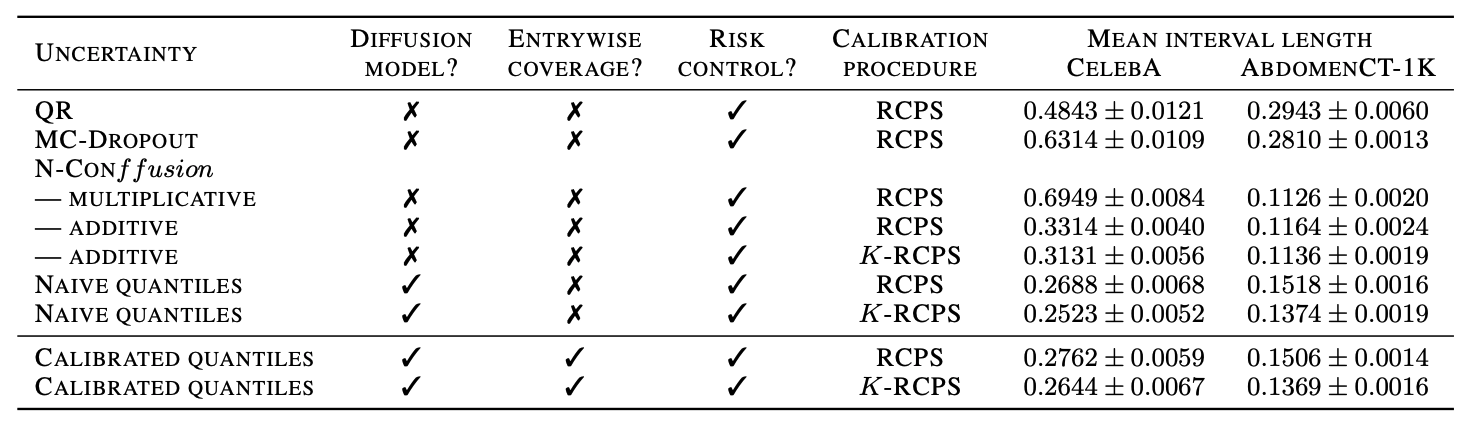
\(K\)-RCPS: High-dimensional Risk Control
scalar \(\lambda \in \mathbb{R}\)
\(\mathcal{I}_{\lambda}(y)_j = [\text{low} - \lambda, \text{up} + \lambda]\)
\(\rightarrow\)
vector \(\bm{\lambda} \in \mathbb{R}^d\)
\(\rightarrow\)
\(\mathcal{I}_{\bm{\lambda}}(y)_j = [\text{low} - \lambda_j, \text{up} + \lambda_j]\)
Guarantee: \(\mathcal{I}_{\bm{\lambda}}(y)_j = [\text{low} - \lambda_j, \text{up} + \lambda_j]\) are RCPS
For a \(K\)-partition of the pixels \(M \in \{0, 1\}^{d \times K}\)
\(K=4\)
\(K=8\)
\(K=32\)
scalar \(\lambda \in \mathbb{R}\)
\(\rightarrow\)
vector \(\bm{\lambda} \in \mathbb{R}^d\)
\(\mathcal{I}_{\lambda}(y)_j = [\text{low} - \lambda, \text{up} + \lambda]\)
\(\rightarrow\)
\(\mathcal{I}_{\bm{\lambda}}(y)_j = [\text{low} - \lambda_j, \text{up} + \lambda_j]\)
1. Solve
\[\tilde{\bm{\lambda}}_K = \arg\min~\sum_{k \in [K]}n_k\lambda_k~\quad\text{s.t. empirical risk} \leq \epsilon\]
2. Choose
\[\hat{\beta} = \inf\{\beta \in \mathbb{R}:~\forall \beta' \geq \beta,~\text{risk}(M\tilde{\bm{\lambda}}_K + \beta') \leq \epsilon\}\]
\(K\)-RCPS: High-dimensional Risk Control
\(\hat{\lambda}_K\)
conformalized uncertainty maps
\(K=4\)
\(K=8\)
\[\mathbb{P}\left[\mathbb{E}\left[\text{fraction of pixels not in intervals}\right] \leq \epsilon\right] \geq 1 - \delta\]
Teneggi, J., Tivnan, M., Stayman, W., & Sulam, J. (2023, July). How to trust your diffusion model: A convex optimization approach to conformal risk control. In International Conference on Machine Learning. PMLR.
\(K\)-RCPS: High-dimensional Risk Control
Thank you
Zhenghan Fang
JHU
Jacopo Teneggi
JHU
Beepul Bharti
JHU
Sam Buchanan
TTIC
Yaniv Romano
Technion
Appendix
\hat x = \arg\min_x \frac 12 \| y - A x \|^2_2 + \hat{R}(x)
Learned Proximal Networks
Convergence guarantees for PnP
x^{t+1} = f_\theta \left(x^t - \eta A^T(Ax^t - y)\right)
- [Sreehari et al., 2016; Sun et al., 2019; Chan, 2019; Teodoro et al., 2019]
Convergence of PnP for non-expansive denoisers. -
[Ryu et al, 2019]
Convergence for close to contractive operators - [Xu et al, 2020]
Convergence of Plug-and-Play priors with MMSE denoisers -
[Hurault et al., 2022]
Lipschitz-bounded denoisers
Theorem (PGD with Learned Proximal Networks)
x^{t+1} = \text{prox}_{\hat R} \left(x^t - \eta A^T(Ax^t - y)\right)
\hat x = \arg\min_x \frac 12 \| y - A x \|^2_2 + \hat{R}(x)
Let \(f_\theta = \text{prox}_{\hat{R}} {\color{grey}\text{ with } \alpha>0}, \text{ and } 0<\eta<1/\sigma_{\max}(A) \) with smooth activations
\text{Then } \exists x^* : \lim_{k\to\infty} x^t = x^* \text{ and }
f_\theta(x^* - \eta A^T(Ax^*-y)) = x^*
(Analogous results hold for ADMM)
Learned Proximal Networks
Convergence guarantees for PnP
\hat x = \arg\min_x \frac 12 \| y - A x \|^2_2 + \hat{R}(x)
Learned Proximal Networks
Convergence guarantees for PnP
x^{t+1} = f_\theta \left(x^t - \eta A^T(Ax^t - y)\right)
- [Sreehari et al., 2016; Sun et al., 2019; Chan, 2019; Teodoro et al., 2019]
Convergence of PnP for non-expansive denoisers. -
[Ryu et al, 2019]
Convergence for close-to-contractive operators - [Xu et al, 2020]
Convergence of Plug-and-Play priors with MMSE denoisers -
[Hurault et al., 2022]
Lipschitz-bounded denoisers
Theorem (PGD with Learned Proximal Networks)
x^{t+1} = \text{prox}_{\hat R} \left(x^t - \eta A^T(Ax^t - y)\right)
\hat x = \arg\min_x \frac 12 \| y - A x \|^2_2 + \hat{R}(x)
Let \(f_\theta = \text{prox}_{\hat{R}} {\color{grey}\text{ with } \alpha>0}, \text{ and } 0<\eta<1/\sigma_{\max}(A) \) with smooth activations
\text{Then } \exists x^* : \lim_{k\to\infty} x^t = x^* \text{ and }
f_\theta(x^* - \eta A^T(Ax^*-y)) = x^*
(Analogous results hold for ADMM)
Learned Proximal Networks
Convergence guarantees for PnP
f \approx \mathbb E[Y|X=x]
X \in \mathcal X \subset \mathbb R^n
Y\in \mathcal Y = \{0,1\}
inputs
responses
f:\mathcal X \to \mathcal Y
\text{For any}~ S \subset [n],~ \text{and a sample } { x} \newline
\text{ define }\tilde{X}_S = [{x_S},X_{S^c}], \text{ where } X_{S^c}\sim \mathcal D_{X_S={x_S}}
predictor
Shap-Explanations
x_S
x:
x_{S^c}
f \approx \mathbb E[Y|X=x]
X \in \mathcal X \subset \mathbb R^n
Y\in \mathcal Y = \{0,1\}
inputs
responses
f:\mathcal X \to \mathcal Y
\text{For any}~ S \subset [n],~ \text{and a sample } { x} \newline
\text{ define }\tilde{X}_S = [{x_S},X_{S^c}], \text{ where } X_{S^c}\sim \mathcal D_{X_S={x_S}}
predictor
Shap-Explanations
x_S
x:
x_{S^c}
\tilde{X}_S:
Shap-Explanations
x_S
x
\tilde{X}_S
f \approx \mathbb E[Y|X=x]
X \in \mathcal X \subset \mathbb R^n
Y\in \mathcal Y = \{0,1\}
inputs
responses
f:\mathcal X \to \mathcal Y
\text{For any}~ S \subset [n],~ \text{and a sample } { x} \newline
\text{ define }\tilde{X}_S = [{x_S},X_{S^c}], \text{ where } X_{S^c}\sim \mathcal D_{X_S={x_S}}
predictor
\displaystyle \phi_i = \sum_{S_j\subseteq [n]\setminus \{i\}} w_j ~ \mathbb E \left[ f(\tilde X_{S_j\cup \{i\}}) - f(\tilde X_{S_j}) \right]
Scott Lundberg and Su-In Lee. A Unified Approach to Interpreting Model Predictions, NeurIPS , 2017
efficiency
nullity
symmetry
exponential complexity
Shap-Explanations
f \approx \mathbb E[Y|X=x]
X \in \mathcal X \subset \mathbb R^n
Y\in \mathcal Y = \{0,1\}
inputs
responses
f:\mathcal X \to \mathcal Y
\text{For any}~ S \subset [n],~ \text{and a sample } { x} \newline
\text{ define }\tilde{X}_S = [{x_S},X_{S^c}], \text{ where } X_{S^c}\sim \mathcal D_{X_S={x_S}}
predictor
\gamma = 2
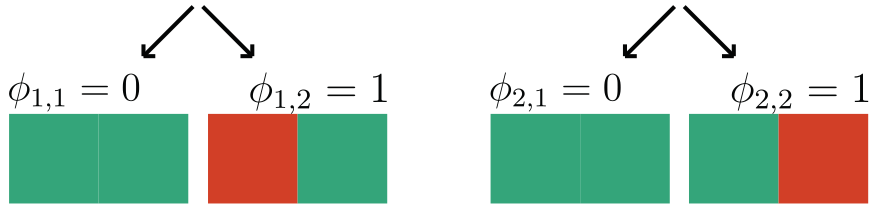
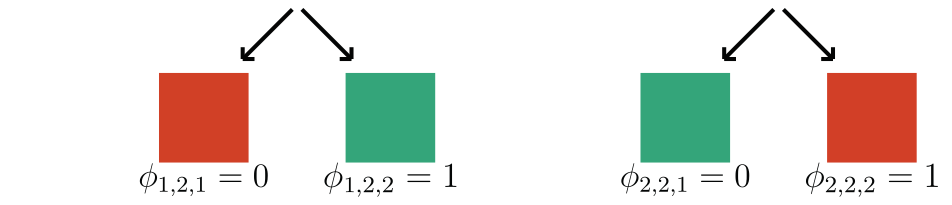
We focus on data with certain structure:
\text{\textbf{Assumption 1:}}~ f^*(x) = 1 \Leftrightarrow \exist~ i: f^*(\tilde X_i) = 1
Theorem (informal)
-
h-Shap runs in linear time
-
Under A1, h-Shap \(\to\) Shapley
\mathcal O(2^\gamma k \log n)
Hierarchical Shap (h-Shap)
Hierarchical Shap (h-Shap)
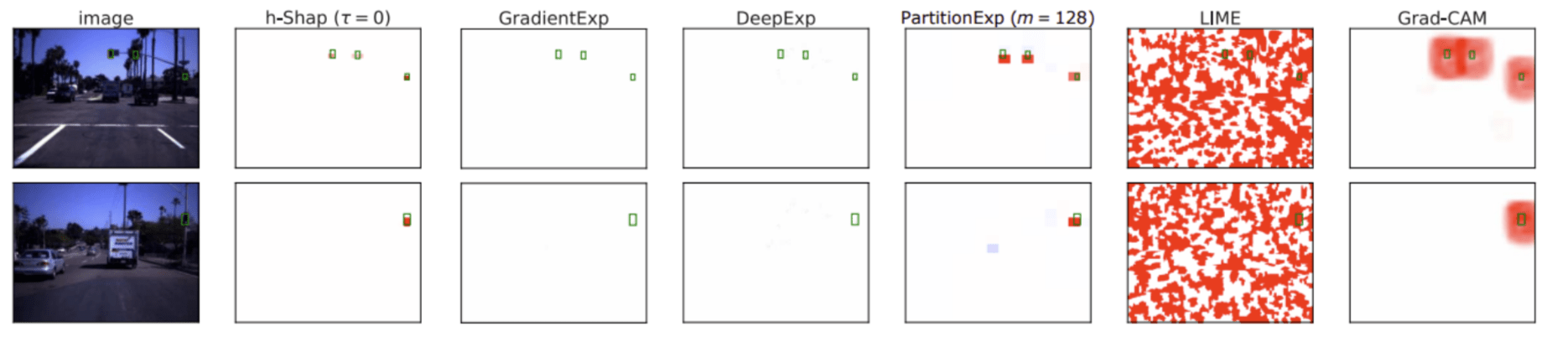
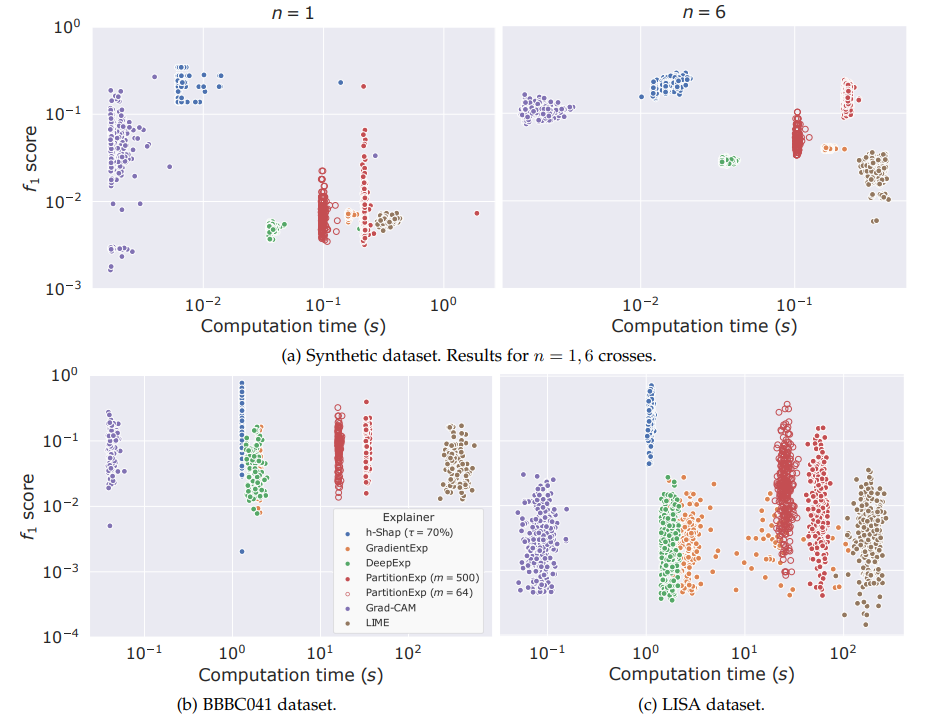
Teneggi, Luster & S. Fast hierarchical games for image explanations, IEEE Transactions on Pattern Analysis and Machine Intelligence, 2022Hierarchical Shap (h-Shap)
[Chattopadhyay et al, 2024]
Cheaper predictors via Interpretability
Hemorrhage detection in head CT
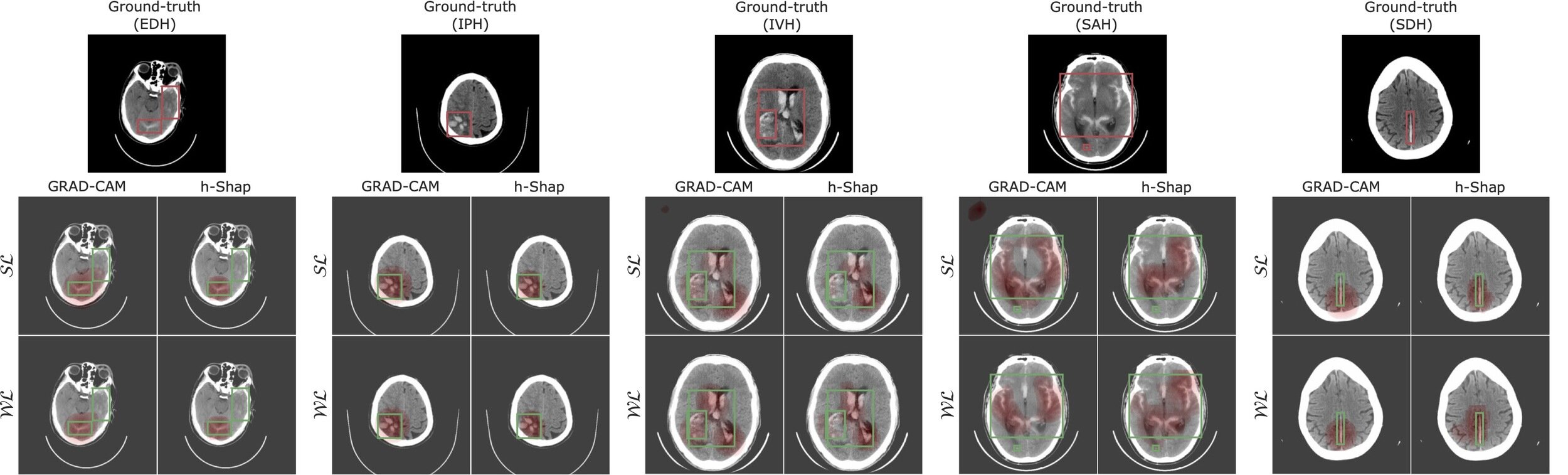
Image-by-image supervision (strong learner)
true/false
Cheaper predictors via Interpretability
Image-by-image supervision (strong learner)
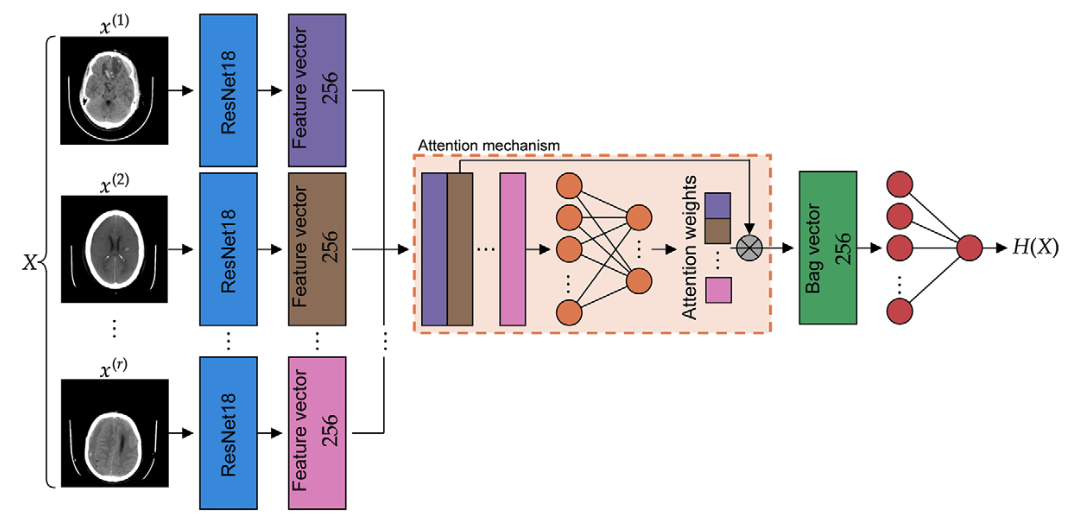
Study/volume supervision (weak learner)
one label per image!
one label per study!
true/false
true/false
Cheaper predictors via Interpretability
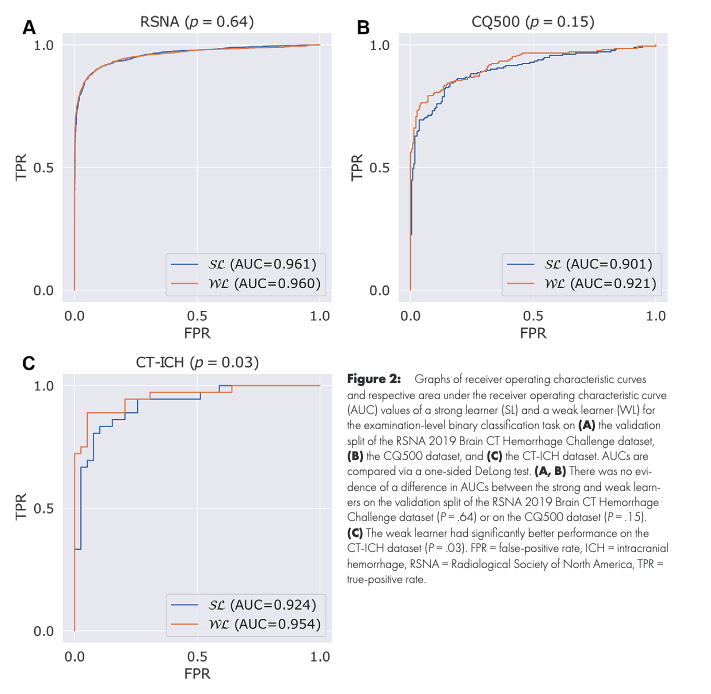
Both methods do as well for case screaning
Teneggi, J., Yi, P. H., & Sulam, J. (2023). Examination-level supervision for deep learning–based intracranial hemorrhage detection at head CT. Radiology: Artificial Intelligence, e230159.
Cheaper predictors via Interpretability
Weak learner is more efficient for detecting positive slices
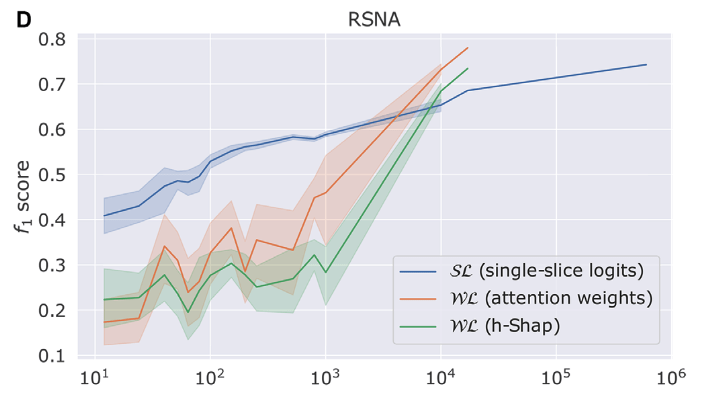
training labels
Teneggi, J., Yi, P. H., & Sulam, J. (2023). Examination-level supervision for deep learning–based intracranial hemorrhage detection at head CT. Radiology: Artificial Intelligence, e230159.
Cheaper predictors via Interpretability
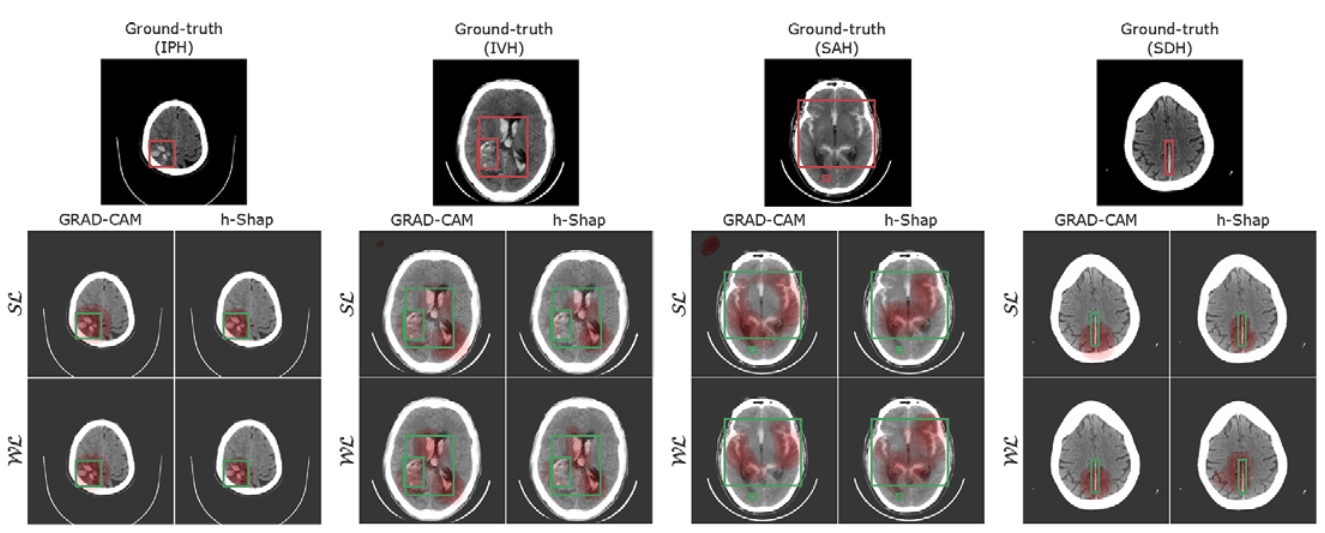
Teneggi, J., Yi, P. H., & Sulam, J. (2023). Examination-level supervision for deep learning–based intracranial hemorrhage detection at head CT. Radiology: Artificial Intelligence, e230159.
Cheaper predictors via Interpretability
What has my model learned (Yale)
By Jeremias Sulam
