On the real cycle class map

\[H^d(X,I^d)\rightarrow H^d(X(\mathbb{R}),\mathbb{Z})\]

Jeremy Jacobson

Wuppertal Topology Seminar 06/16/2021

Outline

Part 1: Real cohomology \[H^{n}(X_r,\mathbb{Z})\] is everywhere
Part 2: Demonstration of a cycle map isomorphism \[H^d(X,I^d)\simeq H^d(X(\mathbb{R}),\mathbb{Z})\] where $d$ is the dimension of $X$.

Jeremy Jacobson

Part 1: Real cohomology is everywhere

Jeremy Jacobson

The cohomological 2-dimension $\text{cd}_2(X_t)$ of $X$ is defined to be the largest integer $n$ for which there is a 2-primary torsion sheaf $A$ on $X_t$ with $H^n(X_t, A) \neq 0$. If no such $n$ exists one writes $\text{cd}_2(X_t) = \infty$

Let $X$ be a scheme. Let $t$ denote a Grothendieck topology, e.g. $t = \{zar, et, r, b\}$.

Part 1: Real cohomology is everywhere

Jeremy Jacobson

Question

If $X$ is noetherian and of Krull dimension $d$, what is $\text{cd}_2(X_{zar})$?

(a) It is $\infty$.

(b) It is not known.

(d) It is less than or equal to the Krull dimension.

Part 1: Real cohomology is everywhere

Jeremy Jacobson

Question

If $X$ is noetherian and of Krull dimension $d$, what is $\text{cd}_2(X_{et})$?

(a) It is $\infty$.

(b) It is less than or equal to $\infty$.

(d) It is less than or equal to the Krull dimension.

Part 1: Real cohomology is everywhere

Jeremy Jacobson

Question

If $X$ is an algebraic variety over the real numbers and $X(\mathbb{R})\neq 0$, what is $\text{cd}_2(X_{et})$?

(a) It is $\infty$.

(b) It is less than or equal to $\infty$.

(d) It is less than or equal to the Krull dimension.

Part 1: Real cohomology is everywhere

Jeremy Jacobson

Question

If $X$ has a point $x$ with residue field which admits an ordering, e.g. $k(x) = \mathbb{Q}$, what is $\text{cd}_2(X_{et})$?

(a) It is $\infty$.

(b) It is less than or equal to $\infty$.

(d) It is less than or equal to the Krull dimension.

Part 1: Real cohomology is everywhere

Jeremy Jacobson

Question

If $X$ has the property that all points $x$ have residue field admitting no ordering, e.g. $k(x) = \mathbb{Q[\sqrt{-1}]}$ or is a finite field, and $\text{cd}_2(X_{et}[\sqrt{-1}]) < \infty$, then what is $\text{cd}_2(X_{et})$?

(a) It is $\infty$.

(b) It is less than or equal to $\infty$.

(d) It is less than or equal to the $\text{cd}_2(X_{et}[\sqrt{-1}])$.

Part 1: Real cohomology is everywhere

Jeremy Jacobson

Question

Let $X$ be a scheme which is q.c.q.s. on which 2 is invertible. Is there a cohomological condition which implies that the etale cohomology $H^*(X_{et},\Z/2)$ is not generated by symbols?

Answer

The real cohomology $H^n(X_r,\mathbb{Z}/2)\neq 0$ for some n. (Corollary 20.2.7.6 in the book by Scheiderer).

Recall that the Milnor conjecture implies that etale cohomology is generated by symbols.

Part 1: Real cohomology is everywhere

Jeremy Jacobson

So what is the real spectrum and real cohomology?

Let $X$ be a scheme. The orderings of all residue fields of X form a topological space called the real spectrum of X. Real cohomology is the sheaf cohomology of this space. It is denoted here $$ H^n(X_r,F)$$ where $F$ is a sheaf on the real spectrum.

Part 1: Real cohomology is everywhere

Jeremy Jacobson

Properties of real cohomology

Let $X$ be a scheme which is q.c.q.s and on which 2 is invertible.

Then $\text{cd}_2(X_r)$ is less than or equal to $\text{cd}_2(X_{zar})$.

Any sheaf for the real topology is a sheaf for the Zariski topology (it is finer).

Further, when $X$ is a real algebraic variety, then $H^n(X_r,\mathbb{Z})$ may be identified with the classical singular cohomology of the real points $H^n_{sing}(X(\mathbb{R}),\mathbb{Z})$.

Part 1: Real cohomology is everywhere

Jeremy Jacobson

Properties of real cohomology

Theorem 7.17 and its corollaries (Scheiderer)

Let $X$ be a scheme which is q.c.q.s and on which 2 is invertible.

There is a map $$ h: H^n(X_{et},\mathbb{Z}/2) \rightarrow \bigoplus_{i=0}^n H^i(X_r,\mathbb{Z}/2)$$ and if $s := \text{cd}_2(X_{et}[\sqrt{-1}]) $ is finite, then this map is bijective for $n\geq s+1$. This is one of the main results, Corollary 7.20, of the book by Scheiderer.

Part 1: Real cohomology is everywhere

Jeremy Jacobson

Questions and conjecture

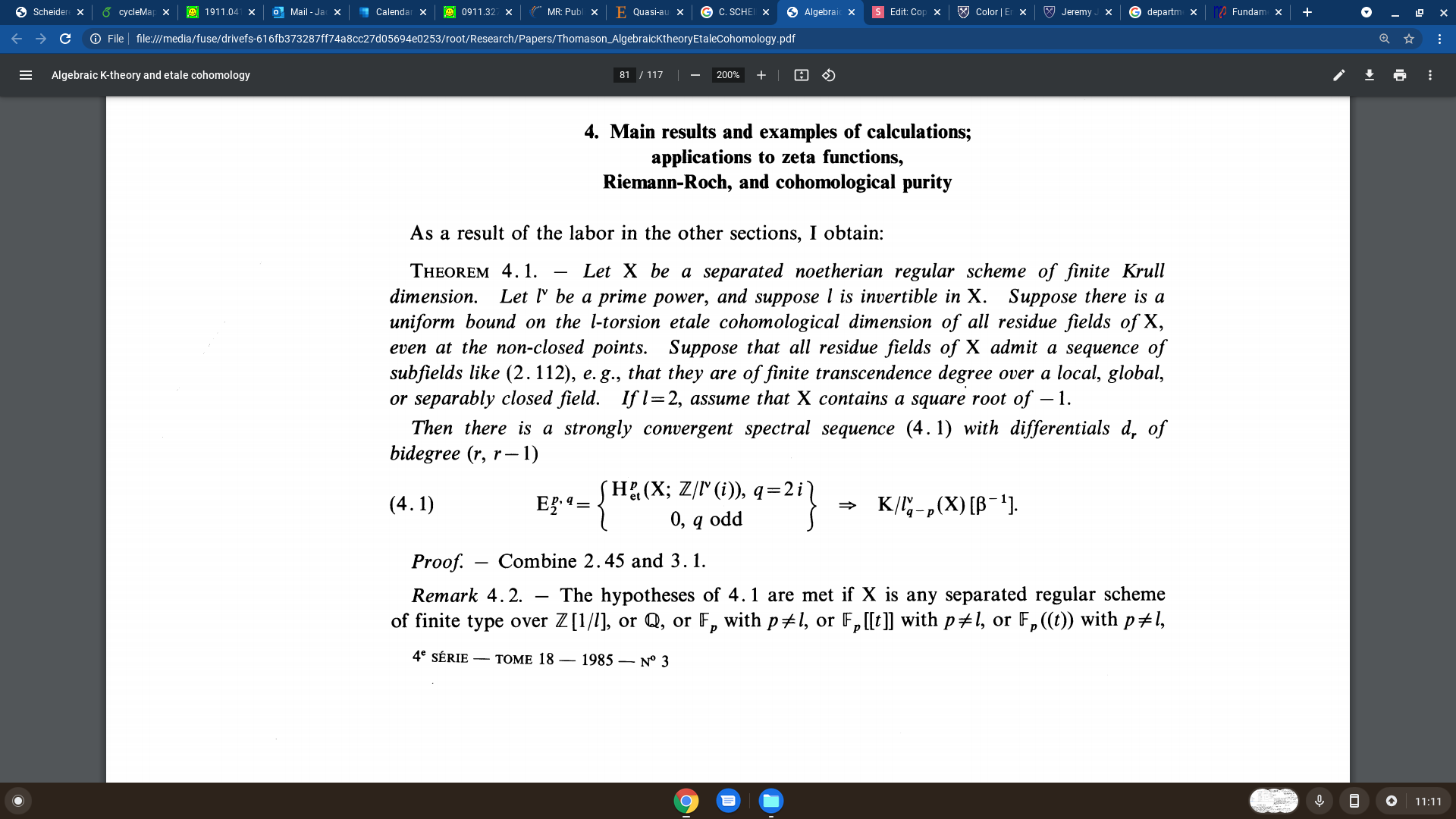
Thomason

Part 1: Real cohomology is everywhere

Jeremy Jacobson

Question

For $l=2$ in Thompson's theorem, can one obtain strong convergence in the spectral sequence without assuming $X$ contains a square root of -1?

For example, suppose instead that $X$ is only separated, noetherian, regular, of finite krull dimension and that $\text{cd}_2(X_{et}[\sqrt{-1}]) < \infty$.

Questions and conjecture

Part 1: Real cohomology is everywhere

Jeremy Jacobson

Properties of real cohomology

Theorem 20.2.13 (Scheiderer)

Let $X$ be a noetherian scheme of finite Krull dimension $d$. Let $s$ denote the supremum over $d$ and $\text{cd}_l(X_{b})$ for all primes $l$. Then for all integers $q > s+1$ the map $h$ defines an isomorphism $$H^n(X_{et},\mathbb{Z}) \cong H^q(X_r,\mathbb{Z}/2) \oplus H^{q-2}(X_r,\mathbb{Z}/2) \oplus H^{q-4}(X_r,\mathbb{Z}/2) \oplus \cdots $$

Part 1: Real cohomology is everywhere

Jeremy Jacobson

Questions and conjecture

Milnor

Let $F$ be a field with an ordering. In his paper Algebraic K-theory and Quadratic forms, Milnor defines a map

$$ K_n^M(F) \rightarrow H^0(X_r,\mathbb{Z}/2)$$

by the correspondence

$$ l(a_1)\times \cdots \times l(a_n) \mapsto \frac{1-\text{sgn}(a_1)}{2} \cdots \frac{1-\text{sgn}(a_n)}{2}$$

In other words, each $l(a)$ is assigned to the map in $H^0(X_r,\mathbb{Z}/2)$ which takes an ordering in $X_r$ and assigns it to $1\in \mathbb{Z}/2$ if $a$ is negative with respect to the ordering and 0 if it $a$ positive.

Part 1: Real cohomology is everywhere

Jeremy Jacobson

Questions and conjecture

Theorem 1.4 (Milnor)

Let $F$ be a field. The element -1 is a sum of squares in $F$ if and only if every positive dimensional element of $K_{*}F$ is nilpotent.

In fact he shows more in the proof, namely if -1 is a sum of $r$ squares, then $l(-1)^{r+1}=0$ and further, for any generator $\gamma = l(a_1)\cdots l(a_n)$, when $n(s-1)>r$ then $\gamma^s=0$.

He also uses it to compute the Milnor k-theory of the real numbers. For all $n\geq 1$, $$K^M_n(\mathbb{R}) \cong H^0(\mathbb{R}_r,\mathbb{Z}/2) \oplus D$$

where $D$ is a divisible group generated by all products $l(a_1)\cdots l(a_n)$ consisting of positive elements $a_1,\cdots,a_n > 0$.

Part 1: Real cohomology is everywhere

Jeremy Jacobson

Questions and conjecture

Tom Bachmann defines a map $K_n^{MW}(F)\rightarrow H^0(F_r,\mathbb{Z}/2)$ by passing through the fundamental ideal and mod 2 Milnor k-theory.

Question

Let $F$ be a field. Can one define a map

$$ K_n^{MW}(F) \rightarrow H^0(X_r,\mathbb{Z})$$

by the correspondence

$$ l(a_1)\times \cdots \times l(a_n) \mapsto \frac{1-\text{sgn}(a_1)}{2} \cdots \frac{1-\text{sgn}(a_n)}{2}$$

and obtain similar results for Milnor-Witt K-theory?

Part 2: The real cycle class map

The origin

Jeremy Jacobson

Part 2: The real cycle class map

Let $X$ be a smooth real variety. There are two ways to obtain a mod 2 cycle map.

The cycle map \[CH^n(X)/2\rightarrow H^n(X(\mathbb{R}),\mathbb{Z}/2)\]
Étale cohomology and the cycle map\[H^n(X_{et},\mathcal{H}^n)\rightarrow H^n(X(\mathbb{R}),\mathbb{Z}/2)\] where $\mathcal{H}^n$ denotes the sheaf associated to the presheaf $U\mapsto H^n(X_{et},\mathbb{Z}/2)$

Jeremy Jacobson

Part 2: The real cycle class map

Let $X$ be a scheme.

There is a map \[H^n(X_{et},\mathcal{H}^n)\rightarrow H^n(X_r,\mathbb{Z}/2)\] induced from a map of sheaves for the Zariski topology \[\mathcal{H}^n \rightarrow H^0(X_r,\mathbb{Z}/2)\]
This map of sheaves is the sheafification of a component $h_0$ of the map $h$ that we saw earlier \[H^n(X_{et},\mathbb{Z}/2) \rightarrow H^0(X_r,\mathbb{Z}/2)\]
When $X$ is a real variety, we obtain the map we saw on the previous slide.

Jeremy Jacobson

Part 2: The real cycle class map

Let $F$ be a field with an ordering.

Given a symmetric form $\beta$ over $F$, after diagonalizing we may count the number of elements on the diagonal that are positive with respect to the ordering and subtract from that count the number that are negative. The resulting integer may be shown to be a well-defined invariant of the form that is called its signature.
Using the signature one defines a map $$W(F) \rightarrow H^0(F_r,\mathbb{Z})$$

Jeremy Jacobson

The signature

Part 2: The real cycle class map

Let $X$ be a scheme.

The Witt ring $W(X)$ of symmetric bilinear forms on $X$ is the Grothendieck group of the abelian monoid of isometry classes of symmetric forms modulo the metabolic spaces.
Using the signature introduced earlier, one may obtain a ring homomorphism $$W(X)\rightarrow H^0(X_r,\mathbb{Z})$$ called the global signature, or just signature.
Here is a sketch of the construction: Given a symmetric space on $X$, we need to assign to every point of the real spectrum an integer. Given such a point $x$, localization produces a morphism $ W(X) \rightarrow W(k(x))$ and we take the signature of the form on $k(x)$ to get our integer in $\mathbb{Z}$.

Jeremy Jacobson

The signature

Part 2: The real cycle class map

Let $X$ be a scheme.

There is a well-defined ring homomorphism $$W(X) \rightarrow H^0(X_r, \mathbb{Z}/2)$$ called the rank, which assigns an isometry class of a symmetric bilinear form $[E, \phi]$ over $X$ to the rank of its underlying vector bundle $E$ modulo 2.
The kernel of the rank map is called the fundamental ideal and is denoted by $I(X)$
The powers of the fundamental ideal are denoted by $I^n(X)$
The sheafification for the Zariski topology of these powers are denoted by $\mathbf{I}^n$

Jeremy Jacobson

Part 2: The real cycle class map

Let $X$ be a scheme.

The signature maps elements of $I^n(X)$ into $H^0(X_r, 2^n\mathbb{Z})$ and dividing by $2^n$ one obtains a map $I^n(X) \rightarrow H^0(X_r, \mathbb{Z})$
The sheafification for the Zariski topology induces a map $$ \mathbf{I}^n \rightarrow H^0(X_r, \mathbb{Z})$$
Taking cohomology we obtain the real cycle class map \[H^m(X,\mathbf{I}^n)\rightarrow H^m(X(\mathbb{R}),\mathbb{Z})\]
For smooth real varieties of dimension $d$, this map is an isomorphism for $n > d$.

Jeremy Jacobson

Part 2: The real cycle class map

Jeremy Jacobson

In a recent paper of Hornbostel, Wendt, Xie, and Zibrowius, for varieties $X$ over a field $F$ with a real embedding $\sigma: F \rightarrow \mathbb{R}$ the full cycle class map is developed and studied.

One aspect of it is the real cycle class map

$$ H^n(X_{Zar},\mathbf{I}^n)\rightarrow H^n_{sing}(X(\mathbb{R}), \Z) $$ induced by the signature.

When $X$ is smooth, affine, and $n=d$, where $d$ is the Krull dimension of $X$, this map is known to be an isomorphism by work of J. Fasel.

Part 2: The real cycle class map

Jeremy Jacobson

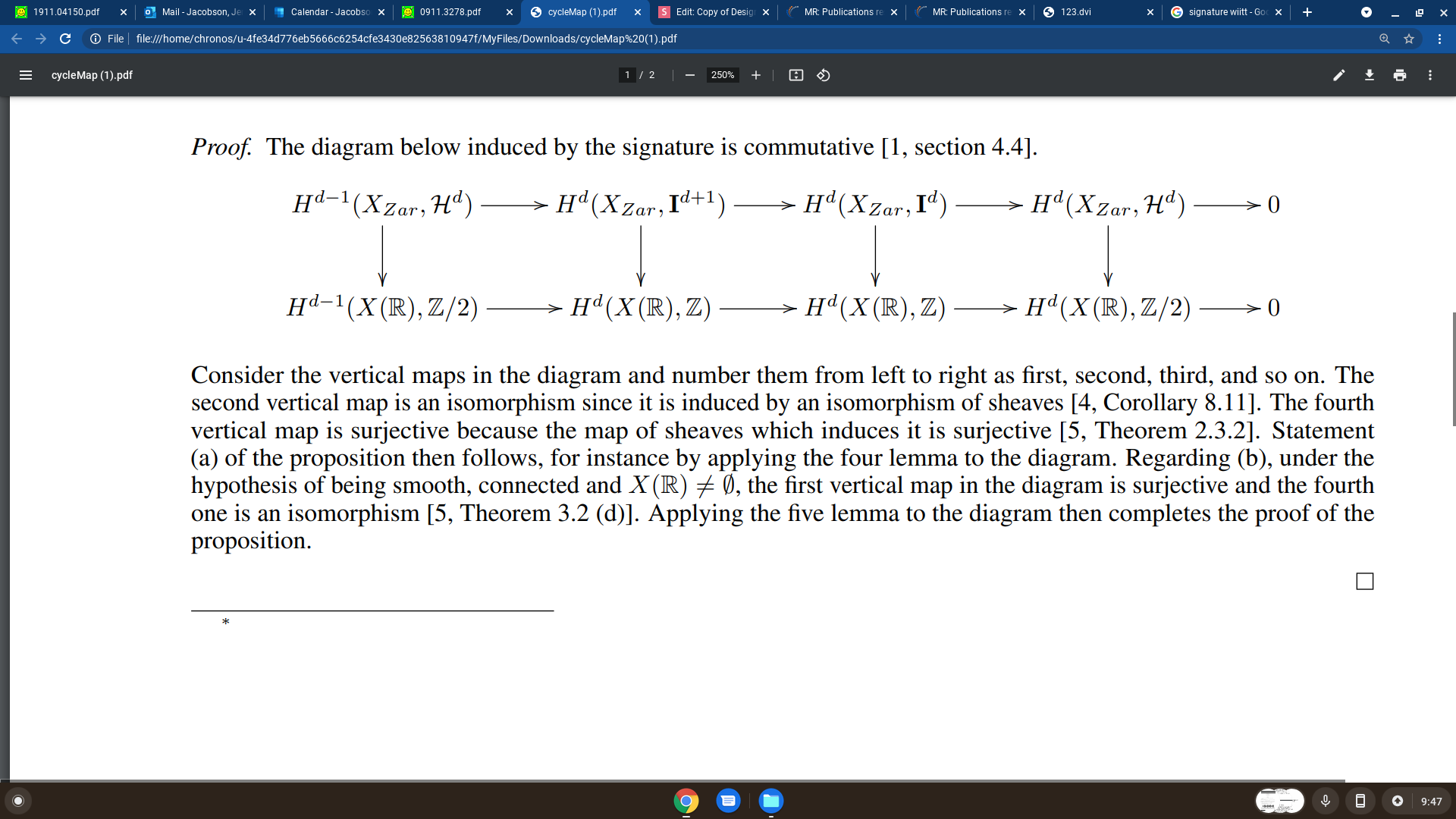
Theorem (Jacobson)

Let $X$ be a real algebraic variety and let $X(\mathbb{R})$ denote the set of real points of $X$ equipped with the analytic topology. Let $d$ denote the Krull dimension of $X$.

The homomorphism of abelian groups $$ H^d(X_{Zar},\mathbf{I}^d)\rightarrow H^d_{sing}(X(\mathbb{R}), \Z) $$ is surjective.
If $X$ is additionally smooth, connected, and $X(\mathbb{R})\neq \emptyset$, then this map is an isomorphism.

Part 2: The real cycle class map

Jeremy Jacobson

Part 2: The real cycle class map

Jeremy Jacobson

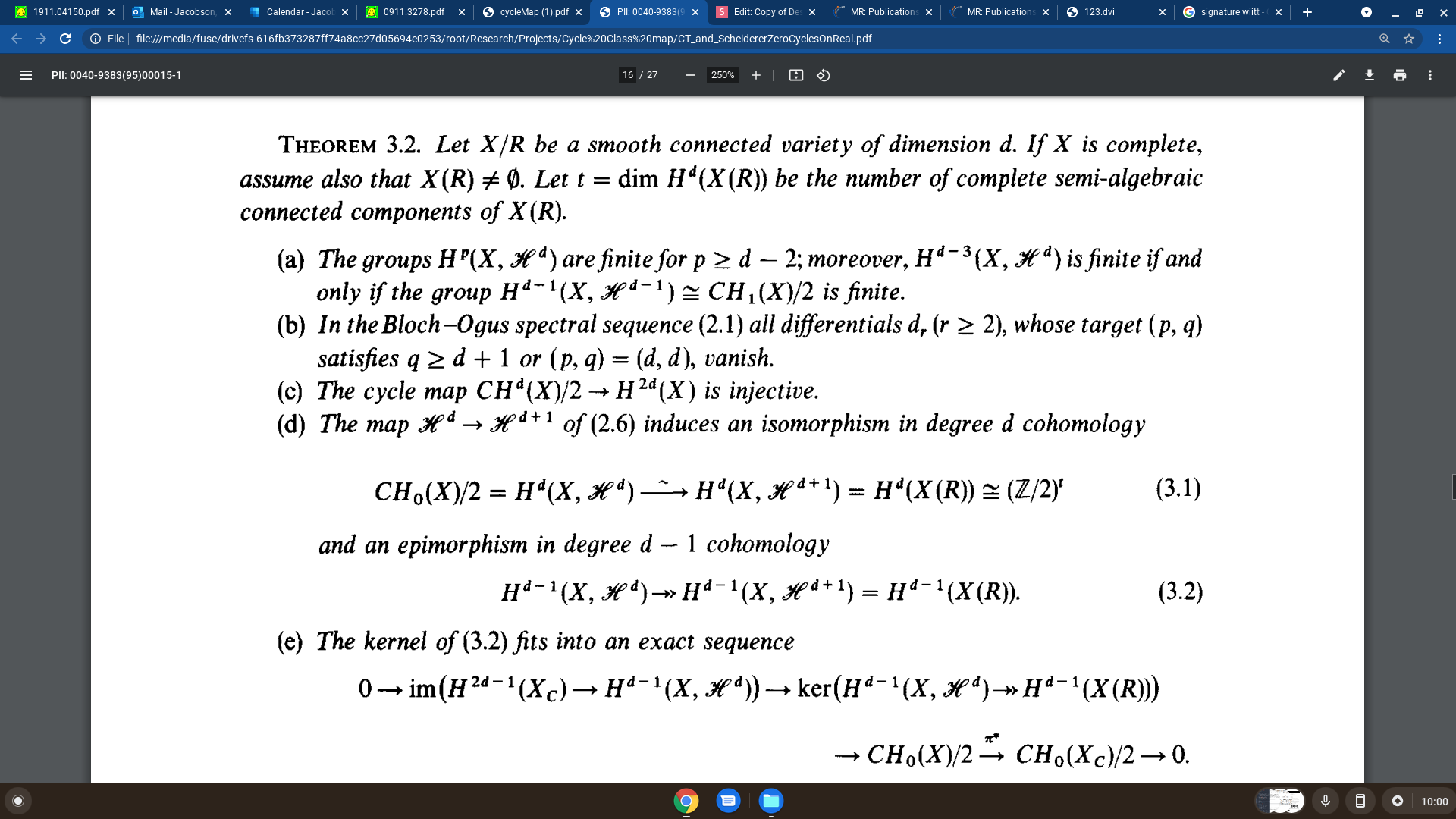
The work of Colliot-Thelene and Scheiderer

Part 2: The real cycle class map

Jeremy Jacobson

The proof of Colliot-Thelene and Scheiderer

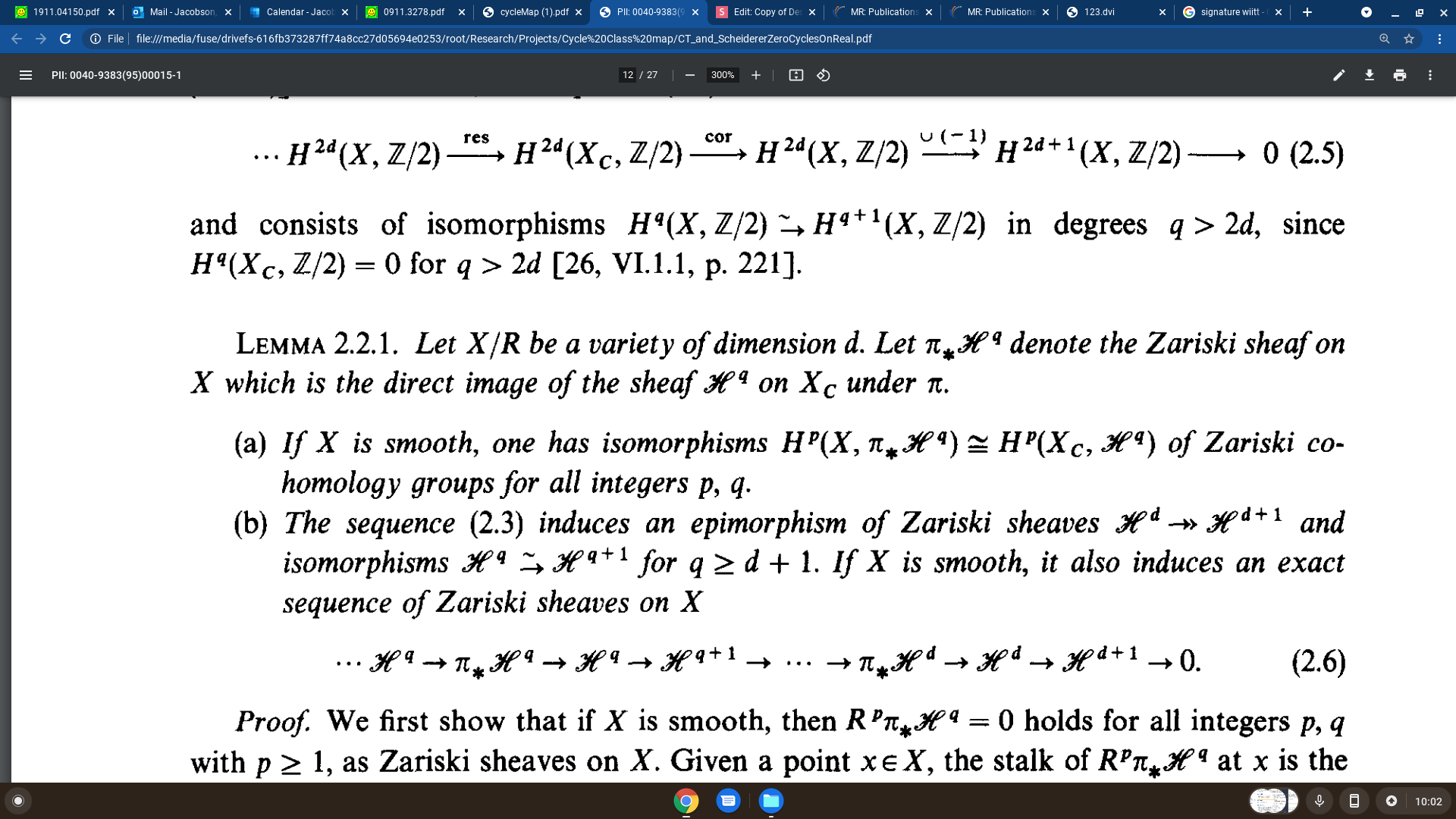
Part 2: The real cycle class map

Jeremy Jacobson

The proof of Colliot-Thelene and Scheiderer

Part 2: The real cycle class map

Jeremy Jacobson

The proof of Colliot-Thelene and Scheiderer

Part 2: The real cycle class map

Jeremy Jacobson

Thank you!

Part 2: The real cycle class map

Jeremy Jacobson

Work in progress

Theorem (J.)

Let $X$ be an affine real variety. Then the real cycle class map is an isomorphism in top degree.

Part 2: The real cycle class map

Jeremy Jacobson

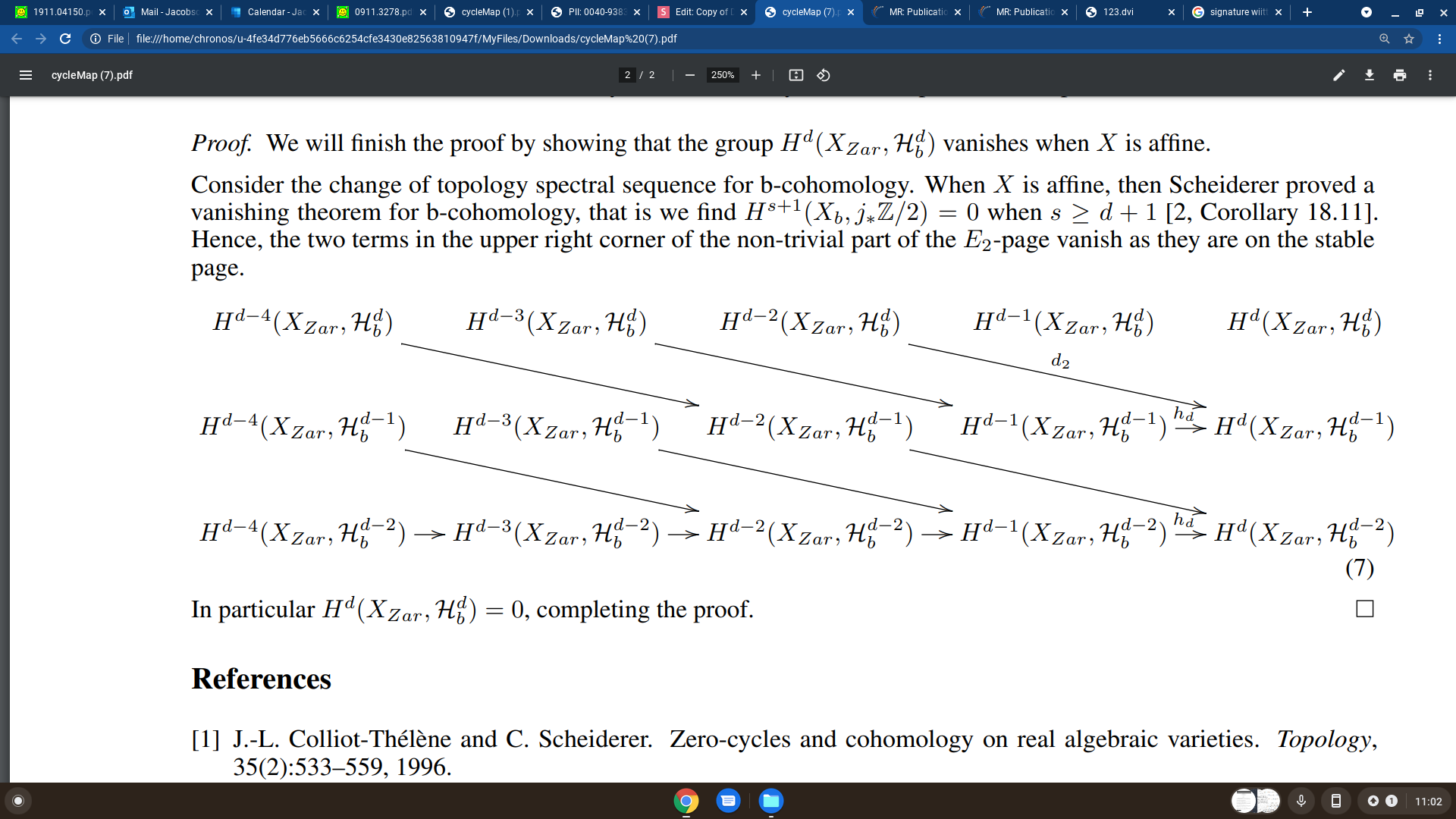
Proof

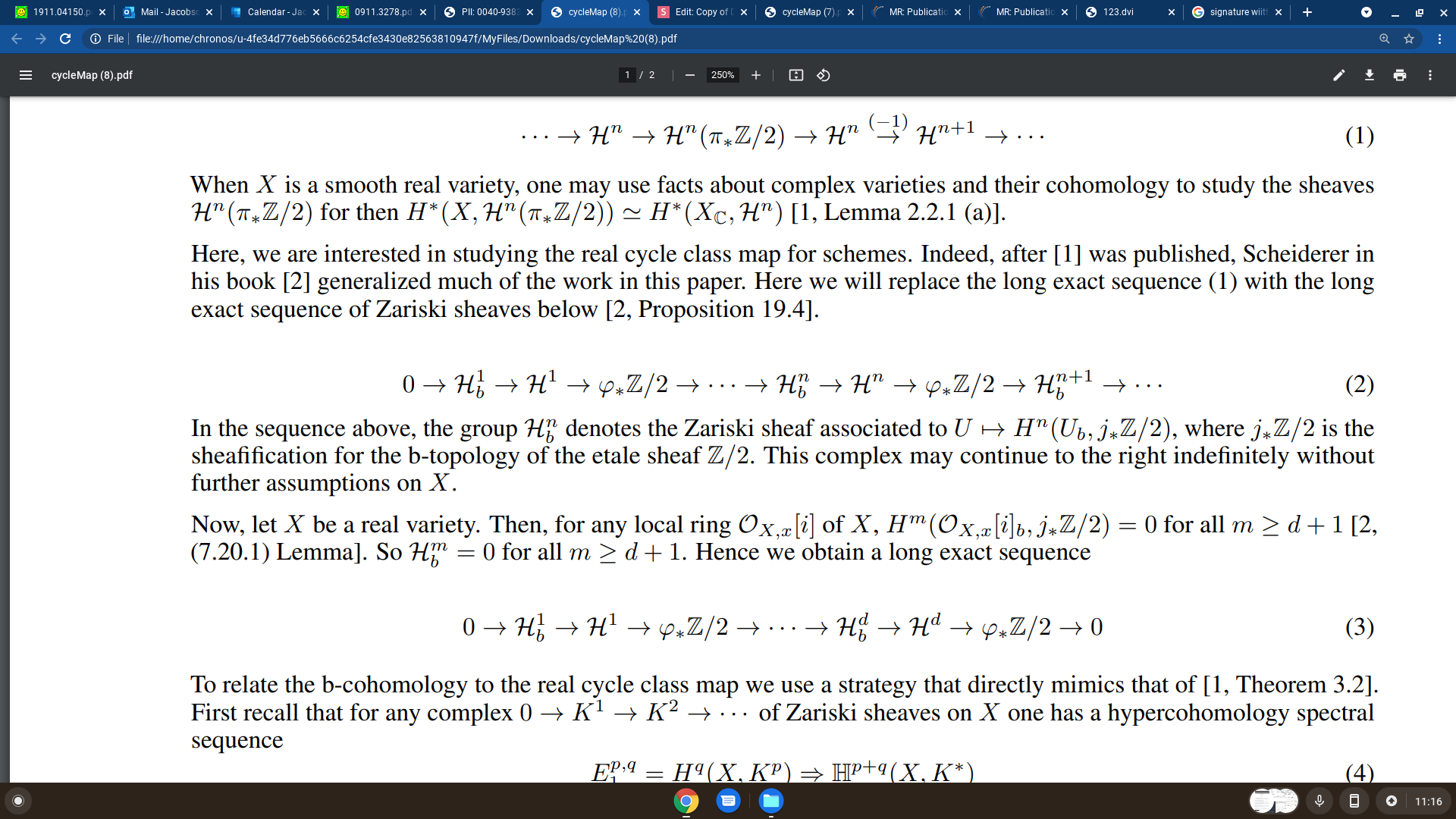
Part 2: The real cycle class map

Jeremy Jacobson

Proof

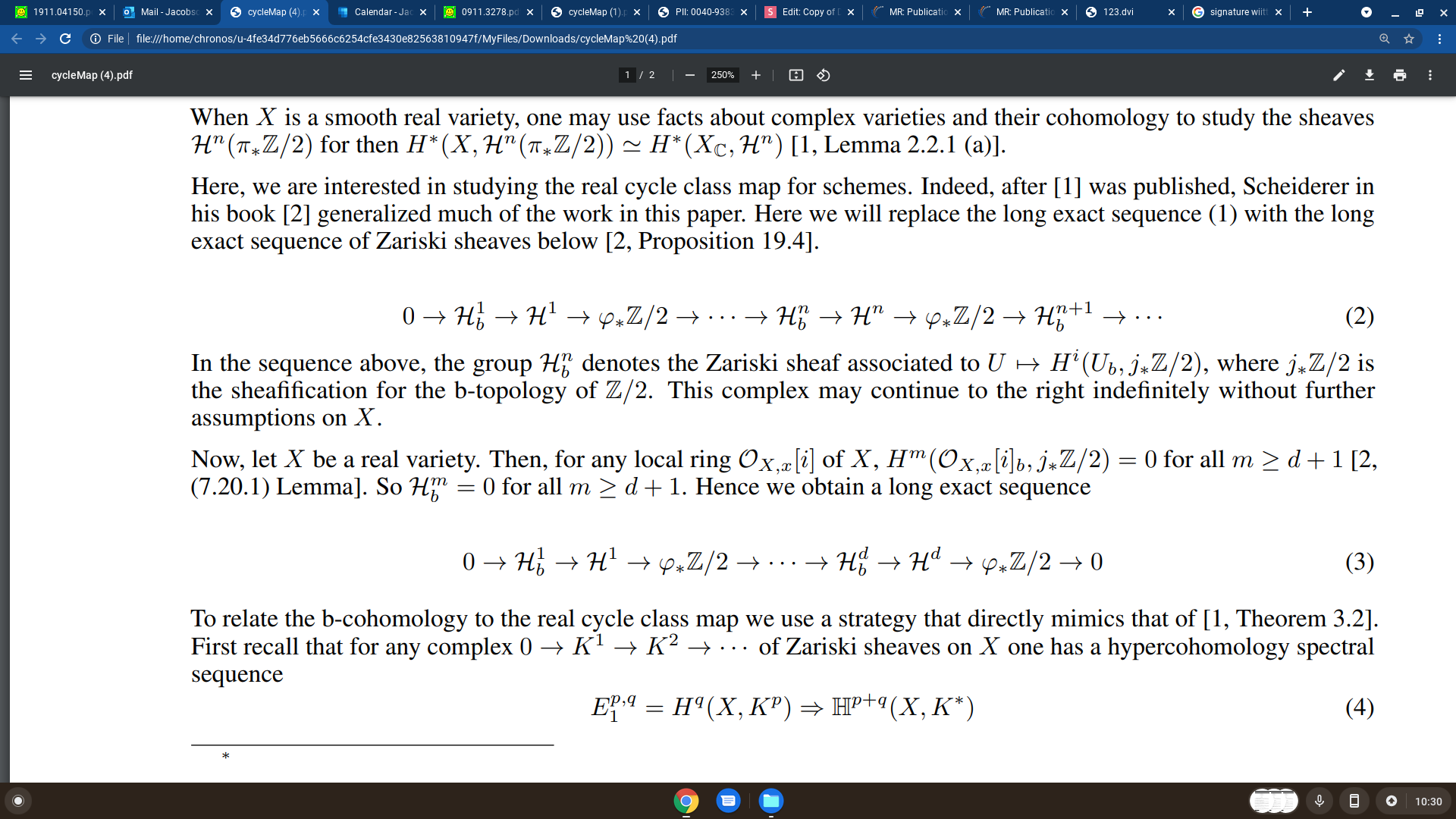
Part 2: The real cycle class map

Jeremy Jacobson

Proof

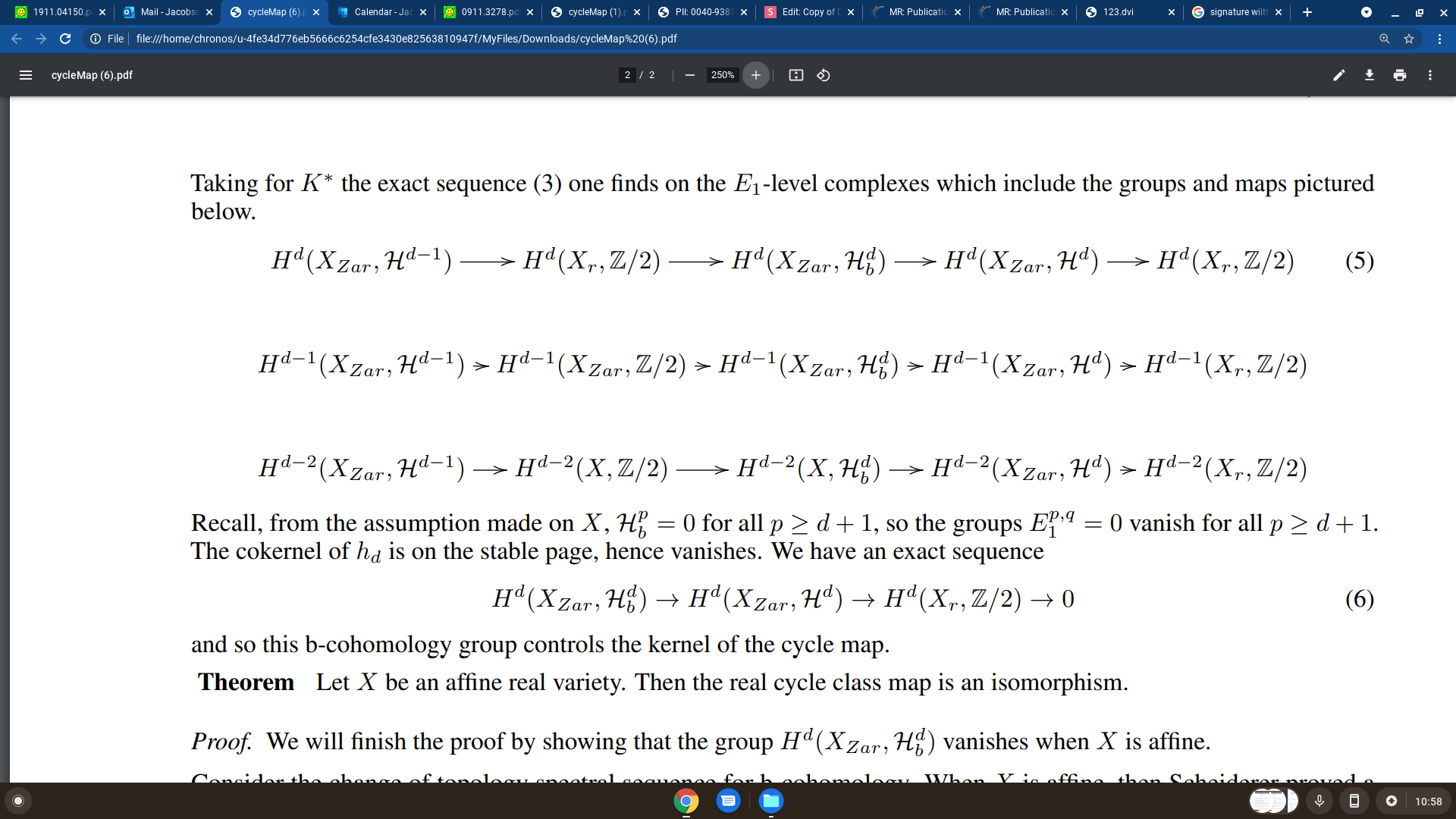
Part 2: The real cycle class map

Jeremy Jacobson

Questions?

Copy of Designing & Building Gutenberg Blocks

By Jeremy Jacobson

Copy of Designing & Building Gutenberg Blocks

Let’s dive in and learn the very basics of building fantastic Gutenberg blocks. We’ll explore the foundations of the block development, setting up a local block development environment, proper user experience techniques within blocks, and how to get involved with the Gutenberg design and technical community. While we won’t go super technical, you’ll leave the session with a clearer understanding of how to design and build Gutenberg blocks.

Jeremy Jacobson

jeremyallenjacobson.github.io

On the real cycle class map

Outline

Part 1: Real cohomology is everywhere

Part 1: Real cohomology is everywhere

Part 1: Real cohomology is everywhere

Part 1: Real cohomology is everywhere

Part 1: Real cohomology is everywhere

Part 1: Real cohomology is everywhere

Part 1: Real cohomology is everywhere

Part 1: Real cohomology is everywhere

So what is the real spectrum and real cohomology?

Part 1: Real cohomology is everywhere

Properties of real cohomology

Part 1: Real cohomology is everywhere

Properties of real cohomology

Part 1: Real cohomology is everywhere

Questions and conjecture

Part 1: Real cohomology is everywhere

Questions and conjecture

Part 1: Real cohomology is everywhere

Properties of real cohomology

Part 1: Real cohomology is everywhere

Questions and conjecture

Part 1: Real cohomology is everywhere

Questions and conjecture

Part 1: Real cohomology is everywhere

Questions and conjecture

Part 2: The real cycle class map

Part 2: The real cycle class map

Part 2: The real cycle class map

Part 2: The real cycle class map

Part 2: The real cycle class map

Part 2: The real cycle class map

Part 2: The real cycle class map

Part 2: The real cycle class map

Part 2: The real cycle class map

Part 2: The real cycle class map

Part 2: The real cycle class map

Part 2: The real cycle class map

Part 2: The real cycle class map

Part 2: The real cycle class map

Part 2: The real cycle class map

Part 2: The real cycle class map

Part 2: The real cycle class map

Part 2: The real cycle class map

Part 2: The real cycle class map

Part 2: The real cycle class map

Questions?

Copy of Designing & Building Gutenberg Blocks

More from Jeremy Jacobson