The Beauty of Equations Visualized With Bokeh and Datashader

Jeremy Jacobson

Lecturer

Institute for Quantitative Theory and Methods (QTM)

Emory University

Andrew Odlyzko (formerly of Bell labs)

Professor

School of Mathematics

 University of Minnesota

C TEST FOR CONVERGENCE UNLESS STAGE 3 HAS FAILED ONCE OR THIS
C IS THE LAST H POLYNOMIAL .
          IF ( BOOL .OR. .NOT. TEST .OR. J .EQ. L2) GO TO 50
          IF (CMOD(TR-OTR,TI-OTI) .GE. .5D0*CMOD(ZR,ZI)) GO TO 40
               IF (.NOT. PASD) GO TO 30
C THE WEAK CONVERGENCE TEST HAS BEEN PASSED TWICE, START THE
C THIRD STAGE ITERATION, AFTER SAVING THE CURRENT H POLYNOMIAL
C AND SHIFT.
                    DO 10 I = 1,N
                         SHR(I) = HR(I)
                         SHI(I) = HI(I)
   10               CONTINUE
                    SVSR = SR
                    SVSI = SI
                    CALL VRSHFT(10,ZR,ZI,CONV)
                    IF (CONV) RETURN
C THE ITERATION FAILED TO CONVERGE. TURN OFF TESTING AND RESTORE
C H,S,PV AND T.
                    TEST = .FALSE.
                    DO 20 I = 1,N
                         HR(I) = SHR(I)
                         HI(I) = SHI(I)
   20               CONTINUE
                    SR = SVSR
                    SI = SVSI
                    CALL POLYEV(NN,SR,SI,PR,PI,QPR,QPI,PVR,PVI)
                    CALL CALCT(BOOL)
                    GO TO 50
   30          PASD = .TRUE.
               GO TO 50
   40     PASD = .FALSE.
   50 CONTINUE
C ATTEMPT AN ITERATION WITH FINAL H POLYNOMIAL FROM SECOND STAGE.
      CALL VRSHFT(10,ZR,ZI,CONV)
      RETURN
      END
      SUBROUTINE VRSHFT(L3,ZR,ZI,CONV)                                  VRSH2230

Bjorn Poonen

Claude Shannon Professor of Mathematics
Algebraic Geometry, Number Theory

Massachusetts Institute of Technology

Bjorn Poonen

Claude Shannon Professor of Mathematics
Algebraic Geometry, Number Theory

Massachusetts Institute of Technology

Trivia Question:

Producing supercomputers and beer are the two primary industries of what city? 

What is

Chippewa Falls, Wisconsin


    What are zeros of polynomials with 0,1 coefficients?

a x^2 + bx + c=0
ax2+bx+c=0a x^2 + bx + c=0

Example

x = \frac{-b \pm \sqrt{b^2-4ac}}{2a}
x=−b±b2−4ac2ax = \frac{-b \pm \sqrt{b^2-4ac}}{2a}

The solutions, a.k.a. roots or zeros, are:

x^2 + x + 1=0
x2+x+1=0x^2 + x + 1=0

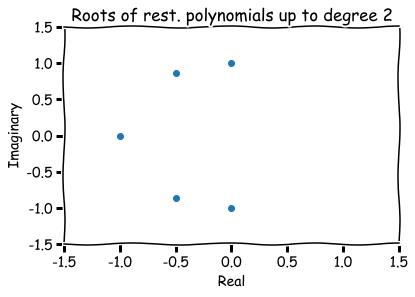
Example (restricted coeff.)

x^2 + 1=0
x2+1=0x^2 + 1=0
(a=1, b=1, c=1)
(a=1,b=1,c=1) (a=1, b=1, c=1)
(a=1,b=0, c=1)
(a=1,b=0,c=1) (a=1,b=0, c=1)
x^2 + x + 1
x2+x+1x^2 + x + 1
x = \frac{-1 + (\sqrt{3})\sqrt{-1}}{2} = \frac{-1}{2} + (\frac{\sqrt{3}}{2})\sqrt{-1}
x=−1+(3)−12=−12+(32)−1x = \frac{-1 + (\sqrt{3})\sqrt{-1}}{2} = \frac{-1}{2} + (\frac{\sqrt{3}}{2})\sqrt{-1}
x^2 + 1
x2+1x^2 + 1
x = \frac{-1 - (\sqrt{3})\sqrt{-1}}{2}= \frac{-1}{2} - (\frac{\sqrt{3}}{2})\sqrt{-1}
x=−1−(3)−12=−12−(32)−1x = \frac{-1 - (\sqrt{3})\sqrt{-1}}{2}= \frac{-1}{2} - (\frac{\sqrt{3}}{2})\sqrt{-1}
x = \frac{0-2\sqrt{-1}}{2}=-\sqrt{-1}
x=0−2−12=−−1x = \frac{0-2\sqrt{-1}}{2}=-\sqrt{-1}
x = \frac{0+2\sqrt{-1}}{2}=\sqrt{-1}
x=0+2−12=−1x = \frac{0+2\sqrt{-1}}{2}=\sqrt{-1}

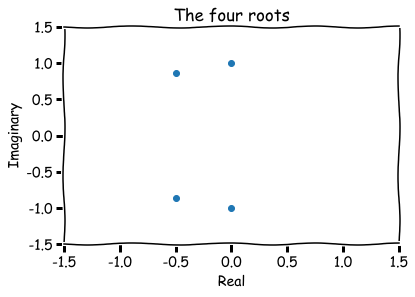
Hence, a finite list of roots (four in total):

How to visualize them?

Fact:

Any root of a polynomial equation can be written in the form

x = a + b \sqrt{-1}
x=a+b−1x = a + b \sqrt{-1}

for some numbers a and b.

 

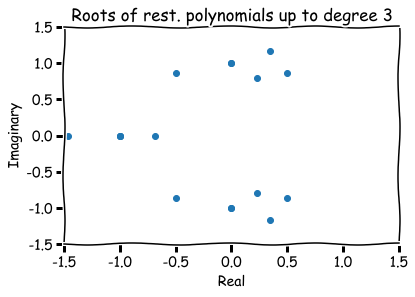
Hence, roots are represented visually by pairs (a,b) in the xy-plane.

 

The number a is called the 'real part' and b the 'imaginary part' of x.

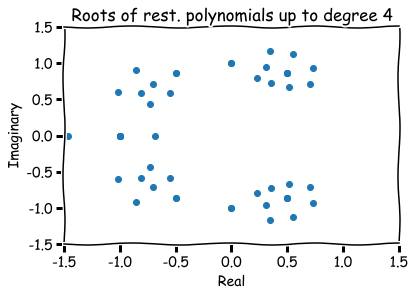
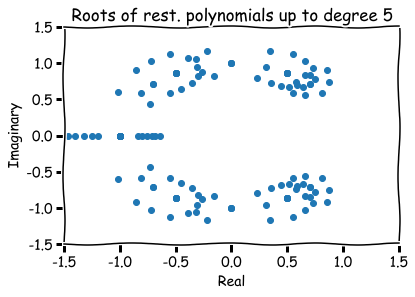
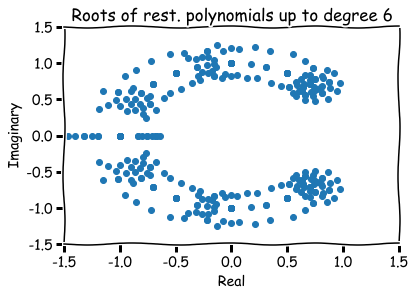
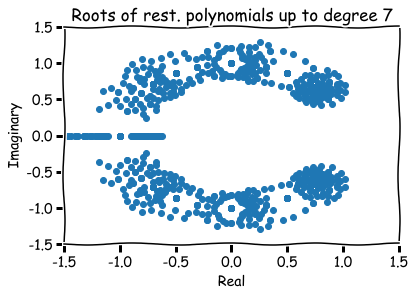
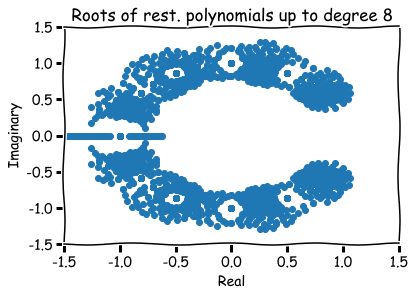
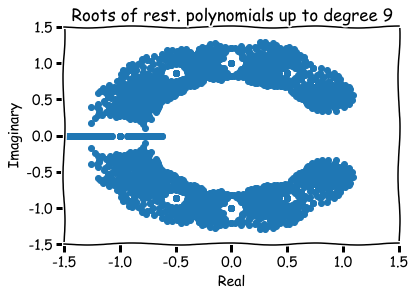
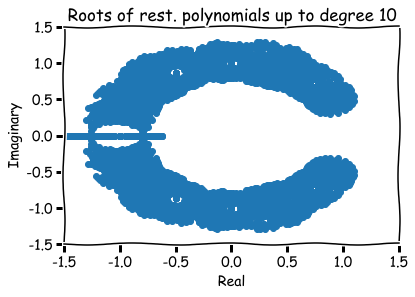
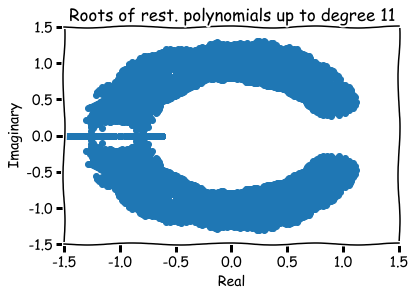
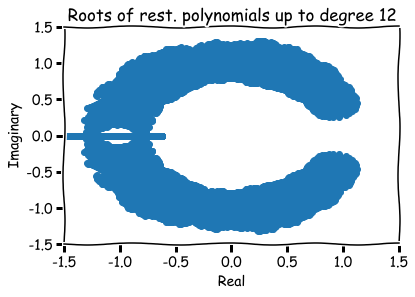
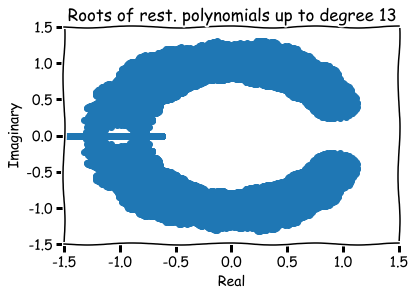
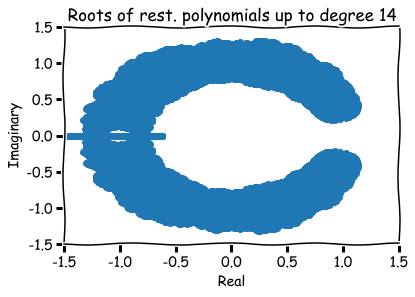
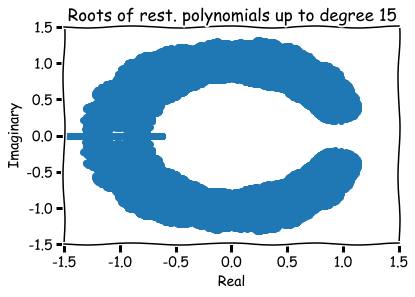
Additional references

The Beauty of Equations Visualized With Bokeh and Datashader

By Jeremy Jacobson

Made with Slides.com

The Beauty of Equations Visualized With Bokeh and Datashader

Introductory slides for the PyData-Atlanta talk given May 30th, 2017,

  • 428

More from Jeremy Jacobson