Combinatorial Programming with Functions

Jo Devriendt

slides.com/jod/manyworlds-orbel

Abstraction in programming

// C
#include <stdio.h>
int main() {
  printf("Hello, World!");
  return 0;
}
# Python
fruits = ["apple", "cherry", "kiwi", "mango"]
newlist = [x.upper() for x in fruits if "a" in x]
-- Haskell
main = print (foldl (-) 0 [1,2,3,4])
# Machine code
b8    21 0a 00 00
a3    0c 10 00 06
b8    6f 72 6c 64
a3    08 10 00 06
; Assembly
_main:
  ; DWORD  bytes;    
  mov     ebp, esp
  sub     esp, 4
   ; hStdOut = GetstdHandle
  push    -11
  call    _GetStdHandle@4
  mov     ebx, eax

Abstraction in programming

Abstract

Close to the metal

  • simple
  • cumbersome
  • efficient
  • encode problem domain
  • rich
  • offloads to compiler
  • slower
  • model problem domain

Link, compile, translate, interprete, emulate...

computational model, Von Neumann architecture

How abstract is
combinatorial programming?

Abstract

Close to the metal

integer programming,
SAT solving, constraint solving

-> solvers

*MPL, OPL, MiniZinc, Essence, FO(.), ASP, ...

low level constraint languages: integer programs, CNF, FlatZinc, ...

Same tradeoffs!

  • An abstract combinatorial programming language
  • Syntax familiar to programmers
  • Simple semantics
  • Multiple inferences
  • Debuggable

ManyWorlds in a nutshell

ManyWorlds example

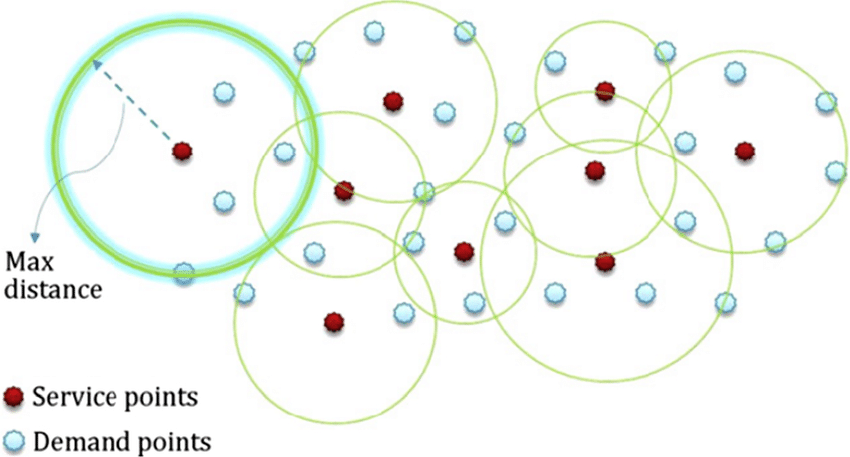
(vertex-restricted) p-centering problem

Hospitals

Communities

ManyWorlds example

declare Community: string -> bool.
define Community as {"c0","c1",...,"c9"} else false.

declare has_hospital: Community -> bool.

count [ has_hospital(c) for c where Community(c) ] <= 3.

declare servicing: Community -> Community.

all [ has_hospital(servicing(c)) for c where Community(c) ].

declare distance: Community,Community -> {0..10000}.
define distance as {("c0","c1",633),("c0","c2",257),...} else 0.

minimize 
  max [ distance(c,servicing(c)) for c where Community(c) ].

ManyWorlds example

declare Community: string -> bool.
define Community as {"c0","c1",...,"c9"} else false.

declare has_hospital: Community -> bool.

count [ has_hospital(c) for c where Community(c) ] <= 3.

declare servicing: Community -> Community.

all [ has_hospital(servicing(c)) for c where Community(c) ].

declare distance: Community,Community -> {0..10000}.
define distance as {("c0","c1",633),("c0","c2",257),...} else 0.

minimize 
  max [ distance(c,servicing(c)) for c where Community(c) ].
  
// condition on hospital placement
has_hospital("c1") xor has_hospital("c2").

ManyWorlds example

declare Community: string -> bool.
define Community as {"c0","c1",...,"c9"} else false.
declare has_hospital: Community -> bool.
count [ has_hospital(c) for c where Community(c) ] <= 3.
declare servicing: Community -> Community.
all [ has_hospital(servicing(c)) for c where Community(c) ].
declare distance: Community,Community -> {0..10000}.
define distance as {("c0","c1",633),("c0","c2",257),...} else 0.
minimize 
  max [ distance(c,servicing(c)) for c where Community(c) ].
// condition on hospital placement
has_hospital("c1") xor has_hospital("c2").

// capacity constraints
declare capacity: Community -> {0..100}.
define capacity as {("c0",15), ("c1",20),...}.

all [ capacity(x) >= 
  count [ x=servicing(y) for y where Community(y) ]
for x where Community(x) ].

Function as building block

First-class functions.

Every expression is a tree of function applications. They can be arbitrarily nested.

Standard builtin functions.
User-declared functions
can be "unknown"/"decision variables".

FMF expression [...] conditionally aggregates n-ary functions.

= != > < >= =< + - * /
not and or xor implies

div rem abs min max count

distinct same if-then-else

Strongly typed and total along bool, int, string

Builtin functions

declare <name>: <type>, <type>, ... -> <finite range>.

User functions

type signature

Function as building block

FMF expressions

all [ has_hospital(servicing(c)) for c where Community(c) ].

Filter: select all c where Community(c) holds

Fold: reduce those has_hospital(serviced_by(c))
 to true iff all are true

Map: map those c to
has_hospital(serviced_by(c))

FMF expressions

all
any
none
count
sum
product
min
max
distinct
same
odd
even
and
or
not or
count
+
*
min
max
distinct
same
xor
not xor

corresponding

n-ary function

Other high-level languages?

Biased opinion: not the same combination of simplicity and accessibility

Can be fixed by "unnesting",
but in ManyWorlds such operations are the task of the compiler.

max [ distance(c,serviced_by(c)) for c where Community(c) ].

ManyWorlds expression:

Similar AMPL expression:

max {c in Community} distance[c,serviced_by[c]]

abstractions are leaky

... but "variables in subscripts are not yet allowed"

Technology

  • Compiled to integer program
  • Solved by Exact
  • Other solvers would be feasible too!
  • Open source implementation

Multiple inferences

find a consistent world

FINDING...

FOUND WORLD
color as {("BE","g"), ("DE","b"), ("FR","r"), ("LU","y"), ("NL","r")}.
declare color: string -> {"r", "g", "b", "y"}.

declare border: string, string -> bool.

define border as {("NL","BE"), ("NL","DE"),
("BE","LU"), ("BE","DE"), ("BE","FR"),
("FR","LU"), ("FR","DE"), ("LU","DE")} else false.

all [ color(x)!=color(y) for x,y where border(x,y) ].

Multiple inferences

count consistent worlds

COUNTING...
#seconds 0.002000
48 world(s) exist.
declare color: string -> {"r", "g", "b", "y"}.

declare border: string, string -> bool.

define border as {("NL","BE"), ("NL","DE"),
("BE","LU"), ("BE","DE"), ("BE","FR"),
("FR","LU"), ("FR","DE"), ("LU","DE")} else false.

all [ color(x)!=color(y) for x,y where border(x,y) ].

Multiple inferences

optimize over all worlds

declare color: string -> {"r", "g", "b", "y"}.

declare border: string, string -> bool.

define border as {("NL","BE"), ("NL","DE"),
("BE","LU"), ("BE","DE"), ("BE","FR"),
("FR","LU"), ("FR","DE"), ("LU","DE")} else false.

all [ color(x)!=color(y) for x,y where border(x,y) ].

minimize count [ color(x)="b" 
	for x where x in {"NL","BE","DE","FR","LU"} ].
FINDING...

FOUND OPTIMAL WORLD
color as {("BE","g"), ("DE","b"), ("FR","r"), ("LU","y"), ("NL","r")}.

OBJECTIVE 1
declare man: string -> bool.
declare mortal: string -> bool.

all [ man(x) implies mortal(x) 
      for x where 
      x in {"Socrates","Athens","poison cup","Zeus"} 
    ].

man("Socrates").
not mortal("Zeus").
INTERSECTING...

FOUND INTERSECTION
man as {("Socrates",true), ("Zeus",false)}.
mortal as {("Socrates",true), ("Zeus",false)}.

intersect all worlds

Multiple inferences

Debugging

debug no consistent world 

FOUND BLOCKERS
Line 9: not color("BE")=color("DE")
Line 9: not color("BE")=color("FR")
Line 9: not color("BE")=color("LU")
Line 9: not color("DE")=color("FR")
Line 9: not color("DE")=color("LU")
Line 9: not color("FR")=color("LU")
declare color: string -> {"r", "g", "b", "y"}.

declare border: string, string -> bool.

define border as {("NL","BE"), ("NL","DE"),
("BE","LU"), ("BE","DE"), ("BE","FR"),
("FR","LU"), ("FR","DE"), ("LU","DE")} else false.

all [ color(x)!=color(y) for x,y where border(x,y) ].

NL is not involved, as it only borders two other countries

Same debug approach for optimality explanation

Debugging

debug expression evaluation 

all [ color(x)!=color(y) for x,y where border(x,y) ].
color("NL") != color("BE") and
color("NL") != color("DE") and
color("BE") != color("LU") and
color("BE") != color("DE") and
color("BE") != color("FR") and
color("FR") != color("LU") and
color("FR") != color("DE") and
color("LU") != color("DE").
"r" != "g" and
"r" != "b" and
"g" != "y" and
"g" != "b" and
"g" != "r" and
"r" != "y" and
"r" != "b" and
"y" != "b".
true and
true and
true and
true and
true and
true and
true and
true.
true.

Why is this expression true for given solution?

same as debugging imperative programs

Implementation pending...

ManyWorlds in a nutshell

  • An abstract combinatorial programming language
  • Syntax familiar to programmers
  • Simple semantics
  • Multiple inferences
  • Debuggable

Motivation

Successful when a 12-year old can do their math homework with ManyWorlds and when a lawyer can recognize ManyWorld-encoded laws.

Caveat: no silver bullet!
But simple problems should have simple solutions.

Problem domain description should match code.

Thanks for your attention!

ManyWorlds - Combinatorial Programming with Functions - ORBEL

By Jo Devriendt

ManyWorlds - Combinatorial Programming with Functions - ORBEL

Presentation of ManyWorlds for Operations Research experts

  • 233

More from Jo Devriendt

  • ManyWorlds - Combinatorial Programming with Functions - ModRef
    Jo Devriendt
    93
  • ManyWorlds - Combinatorial programming with functions
    Jo Devriendt
    341