Conflict-driven cutting plane learning
An OR perspective
Jo Devriendt
ORBEL36
nonfictionsoftware.com
KU Leuven (starting in October)
MIAO group headed by Jakob Nordström
Lund University, Sweden
University of Copenhagen, Denmark
Discussions with Daniel Dadush, Jan Elffers, Stephan Gocht, Janne Kokkala
Acknowledgment
Setting:
Pseudo-Boolean solving
-
Input: 0-1 ILP
-
Output: either
- (optimal) solution
- proof that no solution exists
- PB generalizes Boolean satisfiability (SAT) solving
- Alternative to classic MIP solving for 0-1 ILP
\overline{x}=1-x
2x+y+\overline{z}\geq 2
Constraint propagation
Basic depth-first-search loop
Constraint propagation
Conflict?
Basic depth-first-search loop
Constraint propagation
Conflict?
Decide unassigned variable
no
Basic depth-first-search loop
Constraint propagation
Conflict?
Decide unassigned variable
no
Basic depth-first-search loop
Constraint propagation
Conflict?
Decide unassigned variable
no
Basic depth-first-search loop
Constraint propagation
Conflict?
Learn cutting plane
Decide unassigned variable
yes
no
Basic depth-first-search loop
Constraint propagation
Conflict?
Learn cutting plane
Backjump
Decide unassigned variable
yes
no
Basic depth-first-search loop
Constraint propagation
Conflict?
Learn cutting plane
Backjump
Decide unassigned variable
yes
no
Basic depth-first-search loop
Constraint propagation
Conflict?
Learn cutting plane
Backjump
Decide unassigned variable
yes
no
- Learning constraints pushes search forward
- Thousands of conflicts per second
- Many variations possible
- [Divide and conquer: Towards faster pseudo-boolean solving]
here be dragons
Conflict-driven cutting plane learning
Conflict-driven cutting plane learning
x+y+\overline{z} \geq 1\\
2\overline{y}+2z+\overline{v} \geq 3\\
\overline{z}+2v+\overline{u} \geq 2\\
\overline{x}+2y+u \geq 2\\
u= 1
Constraint propagation
Conflict?
Learn cutting plane
Backjump
Decide unassigned variable
yes
no
Constraint propagation
Conflict?
Learn cutting plane
Backjump
Decide unassigned variable
yes
no
Conflict-driven cutting plane learning
u= 1
x+y+\overline{z} \geq 1\\
2\overline{y}+2z+\overline{v} \geq 3\\
\overline{z}+2v+\overline{u} \geq 2\\
\overline{x}+2y+u \geq 2\\
\rightarrow \overline{x}=1
\rightarrow \overline{y}=z=1
\rightarrow v=1
Constraint propagation
Conflict?
Learn cutting plane
Backjump
Decide unassigned variable
yes
no
Conflict-driven cutting plane learning
u= 1
x+y+\overline{z} \geq 1\\
2\overline{y}+2z+\overline{v} \geq 3\\
\overline{z}+2v+\overline{u} \geq 2\\
\overline{x}+2y+u \geq 2\\
\rightarrow \overline{x}=1
\rightarrow \overline{y}=z=1
\rightarrow v=1
- Conflict: u=1 has no 0-1 solutions
- But rational solution:
- Farkas' lemma: no linear combination that cuts away u=1
z=u=v=1,x=y=0.5
Conflict-driven cutting plane learning
How to learn a cutting plane?
- "Massage" propagating constraints so that decisions + conflict constraint + propagating constraints are rationally infeasible
- Create linear combination per Farkas' lemma
- Add this constraint to database
u= 1
x+y+\overline{z} \geq 1\\
2\overline{y}+2z+\overline{v} \geq 3\\
\overline{z}+2v+\overline{u} \geq 2\\
\overline{x}+2y+u \geq 2\\
\rightarrow \overline{x}=1
\rightarrow \overline{y}=z=1
\rightarrow v=1
Conflict-driven cutting plane learning
1. "Massage" propagating constraints:
-
Divide by propagating literal's coefficient
- Does not affect propagation, except for non-divisible non-falsified literals
- First weaken those by adding variable axioms
- Due to rounding up the RHS, propagation on literal with coef 1 is also rationally implied!
1 \geq x \geq 0
u= 1
x+y+\overline{z} \geq 1\\
2\overline{y}+2z+\overline{v} \geq 3\\
\overline{z}+2v+\overline{u} \geq 2\\
\overline{x}+2y+u \geq 2\\
\rightarrow \overline{y}=z=1
\rightarrow v=1
Ok!
\rightarrow \overline{x}=1
Conflict-driven cutting plane learning
1 \geq x \geq 0
u= 1
x+y+\overline{z} \geq 1\\
2\overline{y}+2z+\overline{v} \geq 3\\
\overline{z}+2v+\overline{u} \geq 2\\
\overline{x}+2y+u \geq 2\\
\rightarrow \overline{x}=1
\rightarrow \overline{y}=z=1
\rightarrow v=1
Not ok!
1. "Massage" propagating constraints:
-
Divide by propagating literal's coefficient
- Does not affect propagation, except for non-divisible non-falsified literals
- First weaken those by adding variable axioms
- Due to rounding up the RHS, propagation on literal with coef 1 is also rationally implied!
Conflict-driven cutting plane learning
1 \geq x \geq 0
u= 1
x+y+\overline{z} \geq 1\\
\textcolor{white}2\overline{y}+\textcolor{white}2z+\overline{v} \geq 2\\
\overline{z}+2v+\overline{u} \geq 2\\
\overline{x}+2y+u \geq 2\\
\rightarrow \overline{x}=1
\rightarrow \overline{y}=z=1
\rightarrow v=1
Not ok!
1. "Massage" propagating constraints:
-
Divide by propagating literal's coefficient
- Does not affect propagation, except for non-divisible non-falsified literals
- First weaken those by adding variable axioms
- Due to rounding up the RHS, propagation on literal with coef 1 is also rationally implied!
Conflict-driven cutting plane learning
1 \geq x \geq 0
u= 1
x+y+\overline{z} \geq 1\\
\textcolor{white}2\overline{y}+\textcolor{white}2z+\overline{v} \geq 2\\
\overline{z}+2v+\overline{u} \geq 2\\
\overline{x}+2y+u \geq 2\\
\rightarrow \overline{x}=1
\rightarrow \overline{y}=z=1
\rightarrow v=1
Ok!
1. "Massage" propagating constraints:
-
Divide by propagating literal's coefficient
- Does not affect propagation, except for non-divisible non-falsified literals
- First weaken those by adding variable axioms
- Due to rounding up the RHS, propagation on literal with coef 1 is also rationally implied!
Conflict-driven cutting plane learning
1 \geq x \geq 0
u= 1
x+y+\overline{z} \geq 1\\
\textcolor{white}2\overline{y}+\textcolor{white}2z+\overline{v} \geq 2\\
\overline{z}+2v+\overline{u} \geq 2\\
\overline{x}+2y+u \geq 2\\
\rightarrow \overline{x}=1
\rightarrow \overline{y}=z=1
\rightarrow v=1
Not ok!
\rightarrow v=1
1. "Massage" propagating constraints:
-
Divide by propagating literal's coefficient
- Does not affect propagation, except for non-divisible non-falsified literals
- First weaken those by adding variable axioms
- Due to rounding up the RHS, propagation on literal with coef 1 is also rationally implied!
Conflict-driven cutting plane learning
1 \geq x \geq 0
u= 1
x+y+\overline{z} \geq 1\\
\textcolor{white}2\overline{y}+\textcolor{white}2z+\overline{v} \geq 2\\
\textcolor{white}{\overline{z}+}2v+\overline{u} \geq 1\\
\overline{x}+2y+u \geq 2\\
\rightarrow \overline{x}=1
\rightarrow \overline{y}=z=1
\rightarrow v=1
Not ok!
\rightarrow v=1
1. "Massage" propagating constraints:
-
Divide by propagating literal's coefficient
- Does not affect propagation, except for non-divisible non-falsified literals
- First weaken those by adding variable axioms
- Due to rounding up the RHS, propagation on literal with coef 1 is also rationally implied!
Conflict-driven cutting plane learning
1 \geq x \geq 0
u= 1
x+y+\overline{z} \geq 1\\
\textcolor{white}2\overline{y}+\textcolor{white}2z+\overline{v} \geq 2\\
\textcolor{white}{\overline{z}+2}v+\overline{u} \geq 1\\
\overline{x}+2y+u \geq 2\\
\rightarrow \overline{x}=1
\rightarrow \overline{y}=z=1
\rightarrow v=1
Not ok!
\rightarrow v=1
1. "Massage" propagating constraints:
-
Divide by propagating literal's coefficient
- Does not affect propagation, except for non-divisible non-falsified literals
- First weaken those by adding variable axioms
- Due to rounding up the RHS, propagation on literal with coef 1 is also rationally implied!
Conflict-driven cutting plane learning
1 \geq x \geq 0
u= 1
x+y+\overline{z} \geq 1\\
\textcolor{white}2\overline{y}+\textcolor{white}2z+\overline{v} \geq 2\\
\textcolor{white}{\overline{z}+2}v+\overline{u} \geq 1\\
\overline{x}+2y+u \geq 2\\
\rightarrow \overline{x}=1
\rightarrow \overline{y}=z=1
\rightarrow v=1
Ok!
\rightarrow v=1
1. "Massage" propagating constraints:
-
Divide by propagating literal's coefficient
- Does not affect propagation, except for non-divisible non-falsified literals
- First weaken those by adding variable axioms
- Due to rounding up the RHS, propagation on literal with coef 1 is also rationally implied!
Conflict-driven cutting plane learning
u= 1
x+y+\overline{z} \geq 1\\
\textcolor{white}2\overline{y}+\textcolor{white}2z+\overline{v} \geq 2\\
\textcolor{white}{\overline{z}+2}v+\overline{u} \geq 1\\
\overline{x}+2y+u \geq 2\\
\rightarrow \overline{x}=1
\rightarrow \overline{y}=z=1
\rightarrow v=1
\rightarrow v=1
2. Create linear combination:
- Start from the conflict constraint
- Add up propagating constraints s.t. propagated variable is eliminated
- backwards chronological (LIFO)
- each addition maintains inconsistency of conflict
- In the end, conflict will be falsified by decisions only
- guaranteed to push search forward
+1x
Conflict-driven cutting plane learning
u= 1
1+3y+\overline{z}+u \geq 3\\
\textcolor{white}2\overline{y}+\textcolor{white}2z+\overline{v} \geq 2\\
\textcolor{white}{\overline{z}+2}v+\overline{u} \geq 1\\
\overline{x}+2y+u \geq 2\\
\rightarrow \overline{x}=1
\rightarrow \overline{y}=z=1
\rightarrow v=1
\rightarrow v=1
+1x
2. Create linear combination:
- Start from the conflict constraint
- Add up propagating constraints s.t. propagated variable is eliminated
- backwards chronological (LIFO)
- each addition maintains inconsistency of conflict
- In the end, conflict will be falsified by decisions only
- guaranteed to push search forward
Conflict-driven cutting plane learning
u= 1
3y+\overline{z}+u \geq 2\\
\textcolor{white}2\overline{y}+\textcolor{white}2z+\overline{v} \geq 2\\
\textcolor{white}{\overline{z}+2}v+\overline{u} \geq 1\\
\overline{x}+2y+u \geq 2\\
\rightarrow \overline{x}=1
\rightarrow \overline{y}=z=1
\rightarrow v=1
\rightarrow v=1
+1x
2. Create linear combination:
- Start from the conflict constraint
- Add up propagating constraints s.t. propagated variable is eliminated
- backwards chronological (LIFO)
- each addition maintains inconsistency of conflict
- In the end, conflict will be falsified by decisions only
- guaranteed to push search forward
Conflict-driven cutting plane learning
u= 1
3y+\overline{z}+u \geq 2\\
\textcolor{white}2\overline{y}+\textcolor{white}2z+\overline{v} \geq 2\\
\textcolor{white}{\overline{z}+2}v+\overline{u} \geq 1\\
\overline{x}+2y+u \geq 2\\
\rightarrow \overline{x}=1
\rightarrow \overline{y}=z=1
\rightarrow v=1
\rightarrow v=1
+1x
2. Create linear combination:
- Start from the conflict constraint
- Add up propagating constraints s.t. propagated variable is eliminated
- backwards chronological (LIFO)
- each addition maintains inconsistency of conflict
- In the end, conflict will be falsified by decisions only
- guaranteed to push search forward
Conflict-driven cutting plane learning
u= 1
2+2y+u+\overline{v} \geq 4\\
\textcolor{white}2\overline{y}+\textcolor{white}2z+\overline{v} \geq 2\\
\textcolor{white}{\overline{z}+2}v+\overline{u} \geq 1\\
\overline{x}+2y+u \geq 2\\
\rightarrow \overline{x}=1
\rightarrow \overline{y}=z=1
\rightarrow v=1
\rightarrow v=1
+1x
2. Create linear combination:
- Start from the conflict constraint
- Add up propagating constraints s.t. propagated variable is eliminated
- backwards chronological (LIFO)
- each addition maintains inconsistency of conflict
- In the end, conflict will be falsified by decisions only
- guaranteed to push search forward
Conflict-driven cutting plane learning
u= 1
2y+u+\overline{v} \geq 2\\
\textcolor{white}2\overline{y}+\textcolor{white}2z+\overline{v} \geq 2\\
\textcolor{white}{\overline{z}+2}v+\overline{u} \geq 1\\
\overline{x}+2y+u \geq 2\\
\rightarrow \overline{x}=1
\rightarrow \overline{y}=z=1
\rightarrow v=1
\rightarrow v=1
+1x
2. Create linear combination:
- Start from the conflict constraint
- Add up propagating constraints s.t. propagated variable is eliminated
- backwards chronological (LIFO)
- each addition maintains inconsistency of conflict
- In the end, conflict will be falsified by decisions only
- guaranteed to push search forward
Conflict-driven cutting plane learning
u= 1
2y+u+\overline{v} \geq 2\\
\textcolor{white}2\overline{y}+\textcolor{white}2z+\overline{v} \geq 2\\
\textcolor{white}{\overline{z}+2}v+\overline{u} \geq 1\\
\overline{x}+2y+u \geq 2\\
\rightarrow \overline{x}=1
\rightarrow \overline{y}=z=1
\rightarrow v=1
\rightarrow v=1
+2x
2. Create linear combination:
- Start from the conflict constraint
- Add up propagating constraints s.t. propagated variable is eliminated
- backwards chronological (LIFO)
- each addition maintains inconsistency of conflict
- In the end, conflict will be falsified by decisions only
- guaranteed to push search forward
Conflict-driven cutting plane learning
u= 1
2+u+2z+3\overline{v} \geq 6\\
\textcolor{white}2\overline{y}+\textcolor{white}2z+\overline{v} \geq 2\\
\textcolor{white}{\overline{z}+2}v+\overline{u} \geq 1\\
\overline{x}+2y+u \geq 2\\
\rightarrow \overline{x}=1
\rightarrow \overline{y}=z=1
\rightarrow v=1
\rightarrow v=1
+2x
2. Create linear combination:
- Start from the conflict constraint
- Add up propagating constraints s.t. propagated variable is eliminated
- backwards chronological (LIFO)
- each addition maintains inconsistency of conflict
- In the end, conflict will be falsified by decisions only
- guaranteed to push search forward
Conflict-driven cutting plane learning
u= 1
u+2z+3\overline{v} \geq 4\\
\textcolor{white}2\overline{y}+\textcolor{white}2z+\overline{v} \geq 2\\
\textcolor{white}{\overline{z}+2}v+\overline{u} \geq 1\\
\overline{x}+2y+u \geq 2\\
\rightarrow \overline{x}=1
\rightarrow \overline{y}=z=1
\rightarrow v=1
\rightarrow v=1
+2x
2. Create linear combination:
- Start from the conflict constraint
- Add up propagating constraints s.t. propagated variable is eliminated
- backwards chronological (LIFO)
- each addition maintains inconsistency of conflict
- In the end, conflict will be falsified by decisions only
- guaranteed to push search forward
Conflict-driven cutting plane learning
u= 1
u+2z+3\overline{v} \geq 4\\
\textcolor{white}2\overline{y}+\textcolor{white}2z+\overline{v} \geq 2\\
\textcolor{white}{\overline{z}+2}v+\overline{u} \geq 1\\
\overline{x}+2y+u \geq 2\\
\rightarrow \overline{x}=1
\rightarrow \overline{y}=z=1
\rightarrow v=1
\rightarrow v=1
+3x
2. Create linear combination:
- Start from the conflict constraint
- Add up propagating constraints s.t. propagated variable is eliminated
- backwards chronological (LIFO)
- each addition maintains inconsistency of conflict
- In the end, conflict will be falsified by decisions only
- guaranteed to push search forward
Conflict-driven cutting plane learning
u= 1
4+2\overline{u}+2z \geq 7\\
\textcolor{white}2\overline{y}+\textcolor{white}2z+\overline{v} \geq 2\\
\textcolor{white}{\overline{z}+2}v+\overline{u} \geq 1\\
\overline{x}+2y+u \geq 2\\
\rightarrow \overline{x}=1
\rightarrow \overline{y}=z=1
\rightarrow v=1
\rightarrow v=1
+3x
2. Create linear combination:
- Start from the conflict constraint
- Add up propagating constraints s.t. propagated variable is eliminated
- backwards chronological (LIFO)
- each addition maintains inconsistency of conflict
- In the end, conflict will be falsified by decisions only
- guaranteed to push search forward
Conflict-driven cutting plane learning
u= 1
2\overline{u}+2z \geq 3\\
\textcolor{white}2\overline{y}+\textcolor{white}2z+\overline{v} \geq 2\\
\textcolor{white}{\overline{z}+2}v+\overline{u} \geq 1\\
\overline{x}+2y+u \geq 2\\
\rightarrow \overline{x}=1
\rightarrow \overline{y}=z=1
\rightarrow v=1
\rightarrow v=1
+3x
2. Create linear combination:
- Start from the conflict constraint
- Add up propagating constraints s.t. propagated variable is eliminated
- backwards chronological (LIFO)
- each addition maintains inconsistency of conflict
- In the end, conflict will be falsified by decisions only
- guaranteed to push search forward
Conflict-driven cutting plane learning
2\overline{u}+2z \geq 3
Excellent constraint to learn:
Fixes u=0, z=1 after backjump
x+y+\overline{z} \geq 1\\
2\overline{y}+2z+\overline{v} \geq 3\\
\overline{z}+2v+\overline{u} \geq 2\\
\overline{x}+2y+u \geq 2\\
How to learn a cutting plane?
- "Massage" propagating constraints so that decisions + conflict constraint + propagating constraints are rationally infeasible
- Create linear combination per Farkas' lemma
- Add this constraint to database
Implementations
-
RoundingSat (original)
gitlab.com/MIAOresearch/roundingsat -
Exact (fork)
gitlab.com/JoD/Exact
Exact features
- Arbitrary precision calculations - 'exact'
- Proof certificates
- Optimization
- Integer variables
- Python interface
- MPS/LP format support
(but watch out with floating point coefficients) - LP solver integration (still 'exact')
- Objective lower bounding
-
RoundingSat (original)
gitlab.com/MIAOresearch/roundingsat -
Exact (fork)
gitlab.com/JoD/Exact
SWOT
- Theoretical strength lies in dual reasoning
- proofs of optimality / unsatisfiability
- implied variable assignments, irreducible inconsistent subsets
- [Verifying Properties of Bit-vector Multiplication Using Cutting Planes Reasoning]
- proof complexity argument
- In practice also when linear relaxation is weak
- but not on CNF input
- [Theoretical and Experimental Results for Planning with Learned Binarized Neural Network Transition Models]
- Weakness is finding good solutions quickly
- however: miplib.zib.de/instance_details_neos-4360552-sangro.html
Conclusion
- Conflict-driven cutting-planes learning as complement to branch, bound, cut, price, ...
- Depth-first search that learns a cut from each conflict
- Strong in dual reasoning
- Fully precise alternative for classic MIP solving
Thanks for your attention!
Always looking for interesting applications :)
[MS96] GRASP - a new search algorithm for satisfiability - Marques-Silva, Sakallah
[BS97] Using CSP lookback techniques to solve real-world SAT instances - Bayardo, Schrag
[WW00] Combining Linear Programming and Satisability Solving for Resource Planning - Wolfman, Weld
[MMZZM01] Chaff: Engineering an efficient SAT solver - Moskewicz, Madigan, Zhao, Zhang, Malik
[P04] Where are the hard knapsack problems? - Pisinger
[CK05] A fast pseudo-Boolean constraint solver - Chai, Kuehlmann
[SS06] Pueblo: A hybrid pseudo-Boolean SAT solver - Sheini, Sakallah
[Dd06] A Fast Linear-Arithmetic Solver for DPLL(T) - Dutertre, de Moura
[FM06] On Solving the Partial MAX-SAT Problem - Fu, Malik
[ABKW08] Constraint Integer Programming: A New Approach to Integrate CP and MIP - Achterberg, Berthold, Koch, Wolter
[LP10] The Sat4j library, release 2.2 - Le Berre, Parrain
[D16] Scheduling and rostering with learning constraint solvers - Downing
[EN18] Divide and conquer: Towards faster pseudo-boolean solving - Elffers, Nordström
[EGNV18] Using Combinatorial Benchmarks to Probe the Reasoning Power of pseudo-Boolean Solvers - Elffers, Giráldez-Cru, Nordström, Vinyals
[ZIB] SoPlex - soplex.zib.de
[PBCOMP] Latest PB competition - www.cril.univ-artois.fr/PB16/
[MIPLIB] The Mixed Integer Programming Library - miplib.zib.de
References
RoundingSat (Exact) performance
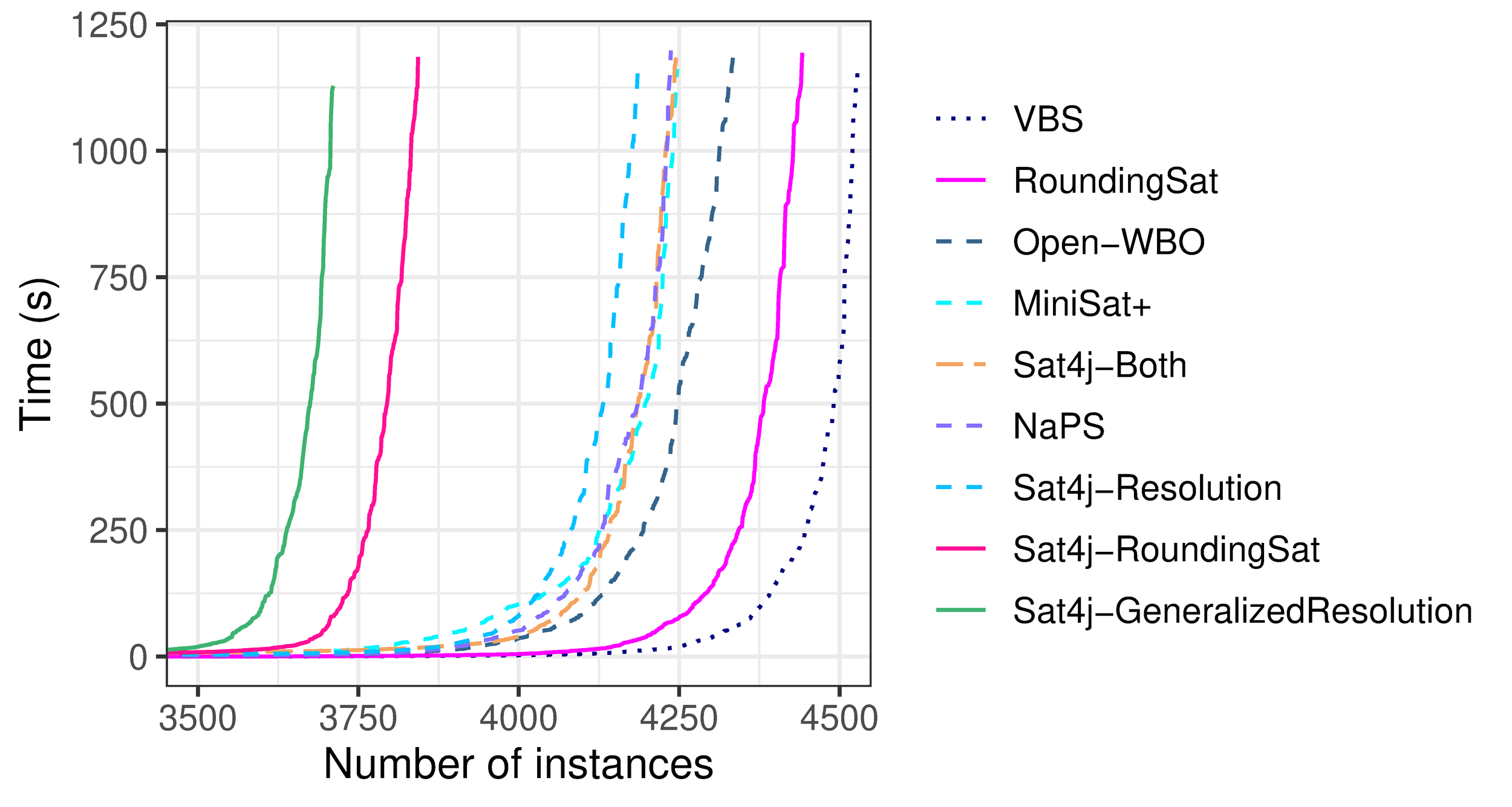
By Romain Wallon (CRIL, Univ Artois & CNRS)
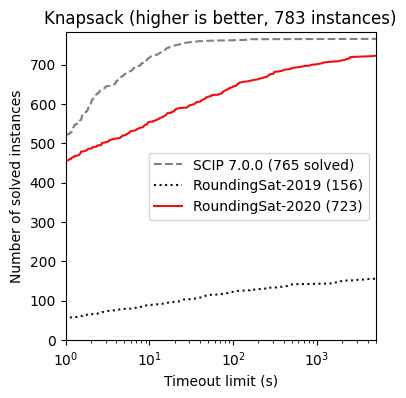
RoundingSat (Exact) performance
RoundingSat (Exact) performance
Copy of Constraint Reasoning, Pseudo-Boolean style
By Jo Devriendt
