Combinatorial Programming with Functions

Jo Devriendt

slides.com/jod/manyworlds-modref

We were all n00bs once...

...with a problem to solve

You were good at high-school math, regularly use spreadsheet formulas.

So you know about
arithmetic formulas and function application.

  • a tournament roster for your sports club
  • a seat arrangement for a wedding
  • a dice odds calculation for a game
  • a class schedule for a school
  • ...

How would you go about this?

ManyWorlds

A friendly, small, simple (??) combinatorial programming language

Basic building blocks:

values

bool, int, string

total functions

type* -> type

Map coloring

FINDING...

FOUND WORLD
define color as {("BE","g"), ("DE","b"), ("FR","r"),
("LU","y"), ("NL","r")} default unknown.
declare color: string -> {"r", "g", "b", "y"}.

color("NL") != color("BE"). color("NL") != color("DE").
color("BE") != color("LU"). color("BE") != color("DE").
color("BE") != color("FR"). color("FR") != color("LU").
color("FR") != color("DE"). color("LU") != color("DE").
  • User functions: uninterpreted functions with a total co-domain [variable(s) (arrays)]
  • Expressions: (nested) function applications
  • Constraints: expressions that must be true
  • Worlds: user function interpretations that make all constraints true [solutions]

Map coloring bis

declare color: string -> {"r", "g", "b", "y"}.

// declare border: string, string -> bool.
decdef border as {("NL","BE"), ("NL","DE"),
("BE","LU"), ("BE","DE"), ("BE","FR"),
("FR","LU"), ("FR","DE"), ("LU","DE")}.

all [ color(x)!=color(y) for x,y where border(x,y) ].

"Fold-Map-Filter" expression

FMF expressions

all [ color(x)!=color(y) for x,y where border(x,y) ].

Filter: select all x,y where border(x,y) holds

Fold: reduce those
color(x)!=color(y)
 to true iff all are true

Map: map those x,y to
color(x)!=color(y)

  • generalize quantification / aggregates
  • take over role of "joker" global constraints - e.g., alldiff_except_0
  • nestable
all
any
none
count
sum
product
min
max
distinct
same
odd
even

More language extensions

Done

  • builtin functions and operators
  • syntactic sugar
  • arbitrary precision integers
  • user types
  • intensional definitions
  • python definitions

To do

  • pseudo-rational division
  • tuple values
  • recursive definitions
  • ...

Inferences & objectives

find
count
intersect

inferences

-  @maximize @minimize @mode

objectives




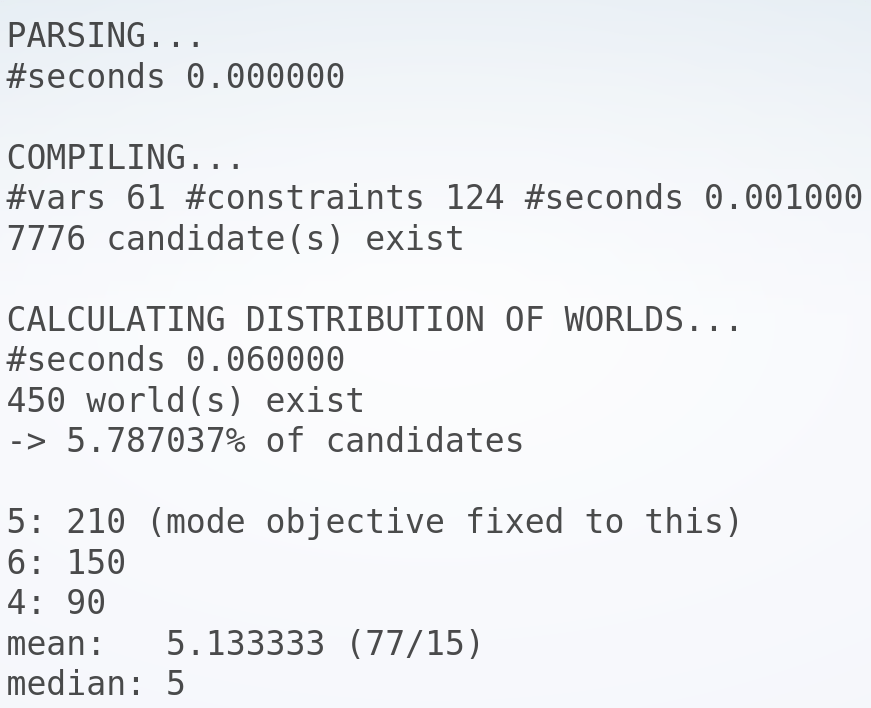
Count + @mode example

Development support

  • online IDE
  • simple syntax highlighting
  • helpful error/warning messages
  • debugging support

(3-valued) expression evaluation

true
true
false
0
18
implies
>=
drinksAlcohol()
age()
18
·   ·   age() [0]
·   >= [false]
·   ·   18
implies [true]
·   drinksAlcohol() [true].

Development support

detailed UNSAT explanation

declare color: string -> {"r", "g", "b", "y"}.

decdef border as {("NL","BE"), ("NL","DE"),
("BE","LU"), ("BE","DE"), ("BE","FR"),
("FR","LU"), ("FR","DE"), ("LU","DE")}.

all [ 
	color(x)!=color(y) 
for x,y where border(x,y) ].
FOUND UNSATISFIABILITY

DETAILED BLOCKERS
Line 7: not color("BE")=color("DE")
Line 7: not color("BE")=color("FR")
Line 7: not color("BE")=color("LU")
Line 7: not color("DE")=color("FR")
Line 7: not color("DE")=color("LU")
Line 7: not color("FR")=color("LU")
FOUND UNSATISFIABILITY

BLOCKERS
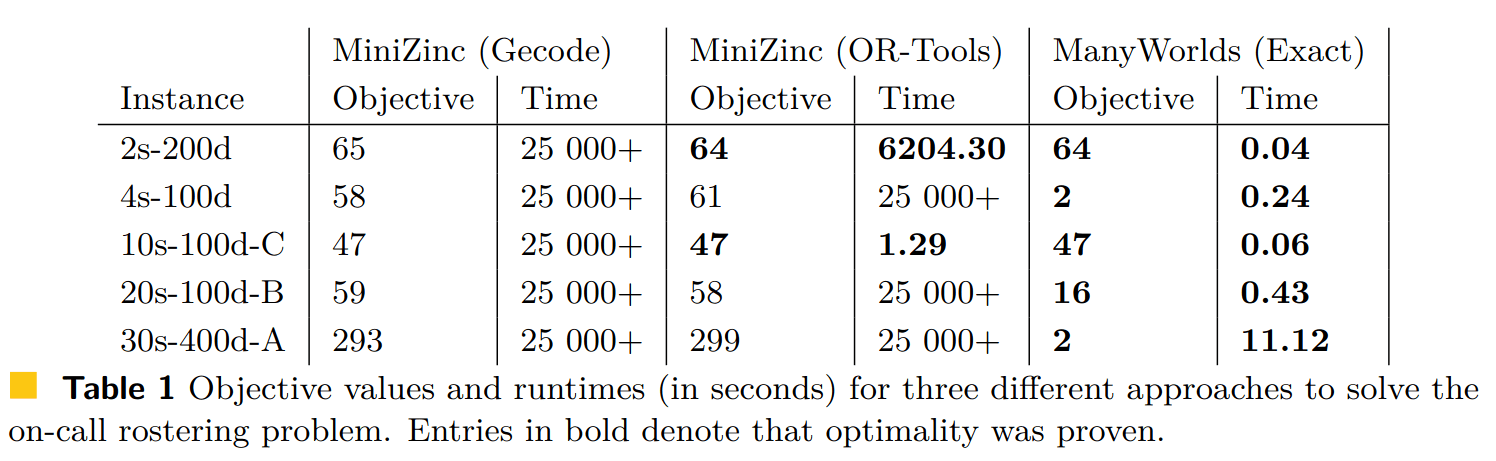
Line 7: all[not color(x)=color(y) for x,y where border(x,y)]

Performance?

Backend solver: Exact

https://gitlab.com/nonfiction-software/exact

On-call rostering

https://github.com/MiniZinc/mzn-challenge/blob/develop/2018/on-call-rostering/oc-roster.mzn

Where to get

Thanks for your attention!

Running


Learning

ManyWorlds - Combinatorial Programming with Functions - ModRef

By Jo Devriendt

ManyWorlds - Combinatorial Programming with Functions - ModRef

Presentation of ManyWorlds for the ModRef workshop

  • 30

More from Jo Devriendt

  • ManyWorlds - Combinatorial Programming with Functions - ORBEL
    Jo Devriendt
    188
  • ManyWorlds - Combinatorial programming with functions
    Jo Devriendt
    282