Combinatorial programming with functions

Jo Devriendt

slides.com/jod/manyworlds-intro

ManyWorlds in a nutshell

Extremely accessible language

With blistering propagation performance

To solve combinatorial problems

Accessible language

3 core ideas

First-class functions

Everything must be finite

bool, int, string primitive types

Online editor @ manyworlds.site

declare S,E,N,D,M,O,R,Y: -> {0..9}.

              1000*S() + 100*E() + 10*N() + D()
            + 1000*M() + 100*O() + 10*R() + E()
//---------------------------------------------
= 10000*M() + 1000*O() + 100*N() + 10*E() + Y().

M() > 0.

distinct(S(),E(),N(),D(),M(),O(),R(),Y()).

Accessible language

declare some 0-arity functions

function that takes arbitrary number of arguments

My mother can understand this. Yours too! :p

write constraints using normal operators

functions

Accessible language

= != > < >= =< + - * / rem
not and or xor implies

abs min max count

distinct same if-then-else

Strongly typed and total along bool, int, string

arguments must be known at compile time for now

overloaded for multiple types

Builtin functions

Accessible language

declare <name>: <type>, <type>, ... -> <finite range>.

User functions

declare prime: int -> {true, false}.

declare distance: string, string -> {0..1000}.

declare cities: string -> bool.

declare state: int -> {"busy", "ready", "down"}.

declare edge_color: string, string -> {"r", "g", "b"}.

signature

all ranges have a clear type, but are finite no int or string

declare n: -> {0..9}.

Accessible language

declare color: string -> {"r", "g", "b", "y"}.

color("NL") != color("BE").
color("NL") != color("DE").
color("BE") != color("LU").
color("BE") != color("DE").
color("BE") != color("FR").
color("FR") != color("LU").
color("FR") != color("DE").
color("LU") != color("DE").

Map coloring 1

There must be a better way...

Accessible language

declare color: string -> {"r", "g", "b", "y"}.

declare border: string, string -> bool.

define border as {("NL","BE"), ("NL","DE"),
("BE","LU"), ("BE","DE"), ("BE","FR"),
("FR","LU"), ("FR","DE"), ("LU","DE")} default false.

all [ color(x)!=color(y) for x,y where border(x,y) ].

Map coloring 2

definition fixes meaning of function

FMF expression

total definition

compiling / flattening / unrolling / grounding / instantiating
yields previous disequalities

Accessible language

FMF expressions

max(f(1), f(2), f(3))
all
any
none
count
sum
product
min
max
distinct
same
odd
even
and
or
not( or )
count
+
*
min
max
distinct
same
xor
not( xor )
max [ f(x) for x where x in {1..3} ]

FMF

corresponding

n-ary function

"scoped builtins"

Accessible language

all [ color(x)!=color(y) for x,y where border(x,y) ].

FMF expressions

Filter: select all x,y where border(x,y) holds

Fold: reduce those color(x)!=color(y) to true iff all are true

Map: map those x,y to color(x)!=color(y)

Accessible language

all [ color(x)!=color(y) for x,y where border(x,y) ].

FMF expressions

list comprehension

aggregate function converting list to one expression

Accessible language

FMF expressions

Flexible!

sum [ 
  weight(x) 
  for x where Item(x) and inKnapsack(x) 
] <= capacity().

Captures global constraints and global functions.

distinct [ 
  color(x) 
  for x where Country(x) and not color(x)="r" 
].

"allDiff except 0"

Accessible language

decdef num as {1..9}.

declare cell: int,int -> num.

all [ 
    distinct [ cell(r,c) for c where num(c) ] 
for r where num(r) ].
all [ 
    distinct [ cell(r,c) for r where num(r) ] 
for c where num(c) ].

declare square: int,int,int -> bool.

define square as ...

all [ 
    distinct [ cell(r,c) for r,c where square(r,c,s)]
for s where num(s) ].

define cell as ...

FMF can be arbitrarily nested

Sudoku

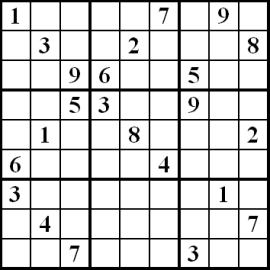
Accessible language

FMF expressions

Write your own decomposition

Circuit constraint in TSP

decdef City as {"city_" 1..n}.

declare next: string -> City.

declare order: string -> {1..n}.

order("city_1") = 1.

all [ order(next(x)) = order(x) + 1 
    for x where City(x) and next(x) != "city_1" ].

Accessible language

decdef City as {"city_" 1..n}.

declare next: string -> City.

declare order: string -> {1..n}.

order("city_1") = 1.

all [ order(next(x)) = order(x) + 1 
    for x where City(x) and next(x) != "city_1" ].

FMF caveat: compiler must derive finite instantiation from "where" block

City limits instantations of x as it is a finite set of strings.

Accessible language

3 core ideas

First-class functions

Everything must be finite

bool, int, string primitive types

Online editor @ manyworlds.site

Solve combinatorial problems

find a consistent world

FOUND WORLD

color as {("DE","b"), ("BE","g"), ("FR","r"), ("LU","y"), ("NL","r")}.

declare color: string -> {"r", "g", "b", "y"}.

declare border: string, string -> bool.

define border as {("NL","BE"), ("NL","DE"),
("BE","LU"), ("BE","DE"), ("BE","FR"),
("FR","LU"), ("FR","DE"), ("LU","DE")} default false.

all [ color(x)!=color(y) for x,y where border(x,y) ].

Solve combinatorial problems

debug no consistent world

FOUND BLOCKERS
Line 9: not color("BE")=color("DE")
Line 9: not color("BE")=color("FR")
Line 9: not color("BE")=color("LU")
Line 9: not color("DE")=color("FR")
Line 9: not color("DE")=color("LU")
Line 9: not color("FR")=color("LU")
declare color: string -> {"r", "g", "b", "y"}.

declare border: string, string -> bool.

define border as {("NL","BE"), ("NL","DE"),
("BE","LU"), ("BE","DE"), ("BE","FR"),
("FR","LU"), ("FR","DE"), ("LU","DE")} default false.

all [ color(x)!=color(y) for x,y where border(x,y) ].

NL is not involved, as it only borders two other countries

Solve combinatorial problems

optimize over all worlds

@minimize sum [ distance(x,next(x)) for x where City(x) ].

find a world now returns

  • optimal world
  • optimal objective value
  • "optimization blockers"

Solve combinatorial problems

declare man: string -> bool.
declare mortal: string -> bool.

all [ man(x) implies mortal(x) 
      for x where 
      x in {"Socrates","Athens","poison cup","Zeus"} 
    ].

man("Socrates").
not mortal("Zeus").
FOUND INTERSECTION

man as {("Socrates",true), ("Zeus",false)} default unknown.

mortal as {("Socrates",true), ("Zeus",false)} default unknown.

intersect all worlds

Solve combinatorial problems

// we have 5 dice
decdef die as {"d" 1..5}.
// with 1 to 6 dots
decdef dots as {1..6}.
// rolling assigns a number of dots to each die
declare roll: die -> dots.
// the sum of the dice rolls must be 14
sum[ roll(x) for x where die(x) ] = 14.
// at most two dice can have rolled the same dots
all [ 2 >= count [ roll(x) = y for x where die(x) ] 
  for y where dots(y) ].
7776 candidate(s) exist.
COUNTING WORLDS...
450 world(s) exist.

count all worlds

Solve combinatorial problems

// we have 5 dice ...

// show the most common value ('mode') of the highest die
// this also yields statistics on the highest die
@mode max[ roll(x) for x where die(x) ].
7776 candidate(s) exist.
CALCULATING DISTRIBUTION OF WORLDS...
450 world(s) exist.
5: 210 (mode objective fixed to this)
6: 150
4: 90
mean: 77/15
median: 5

count all worlds, with statistics!

Solve combinatorial problems

declare drinksAlcohol: -> bool.
declare age: -> {0..150}.
age() >= 18 implies drinksAlcohol().

Evaluate an expression in a world

A common beginner mistake is to invert the implication. Here it means that everyone greater than 18 must drink alcohol...

define drinksAlcohol() as true.
define age() as 0.

The system returns an
"incorrect world":

· · age() [0]
· >= [false]
· · 18
implies [true]
· drinksAlcohol() [true].

Evaluating the constraint that should invalidate this world may reveal the mistake:

Performance

Long term goal

Tools

  • C++
  • Exact
  • multithreaded propagation
  • strong compilation

Fastest "intersect" on the planet

Compilation?

Pipeline

  1. fix parsing
  2. desugar
  3. simplify
  4. instantiate
  5. simplify
  6. unnest 1
  7. simplify
  8. merge
  9. unnest 2
  10. add constraints to solver

Bad: in each step, full expression tree is rebuilt...

Good: minimal set of compiled constraints

Performance

ManyWorlds in a nutshell

Extremely accessible language

With blistering propagation performance

To solve combinatorial problems

Motivation

Combinatorial programming is simpler than imperative programming. Why are the languages so hard?

Successful when a 12-year old can do their math homework with ManyWorlds and when a lawyer can recognize ManyWorld-encoded laws.

Caveat: no silver bullet!
But simple problems should have simple solutions.

Problem domain description should match code.

Usability

  • No order on expressions
    • e.g., use a function before you declare it
  • Deterministic
  • Helpful debug information
    • syntax mistakes
    • compilation errors
    • blockers
    • evaluation engine
  • Online editor
  • Syntax highlighting
  • No limit on integer type
  • Good documentation and tutorials (... to-do)
  • ...

Little directionality

sum [ distance(x,next(x)) for x where City(x) ]
  • order of expressions does not matter
  • (almost) no distinction between
    "known parameters" and "unknown variables"

     
  • even definitions can be used backwards
declare fib: int -> {0..1e21}.


define fib(x) where x in {0..100} as
  0   if x=0 else
  1   if x=1 else
  fib(x-1) + fib(x-2)
default 0.
declare fib: int -> {0..1e21}.
declare a,b: -> {0..10}.

define fib(x) where x in {0..100} as
  a() if x=0 else
  b() if x=1 else
  fib(x-1) + fib(x-2)
default 0.

fib(10)=144.

Thanks for your attention!

ManyWorlds - Combinatorial programming with functions

By Jo Devriendt

ManyWorlds - Combinatorial programming with functions

  • 224

More from Jo Devriendt