Lecture 8:
Some Theorems about \(\varepsilon\)-neighborhoods
Theorem 2.2.8. Let \(a\) and \(x\) be real numbers. If \(x\in V_{\varepsilon}(a)\) for all \(\varepsilon>0\), then \(x=a\).
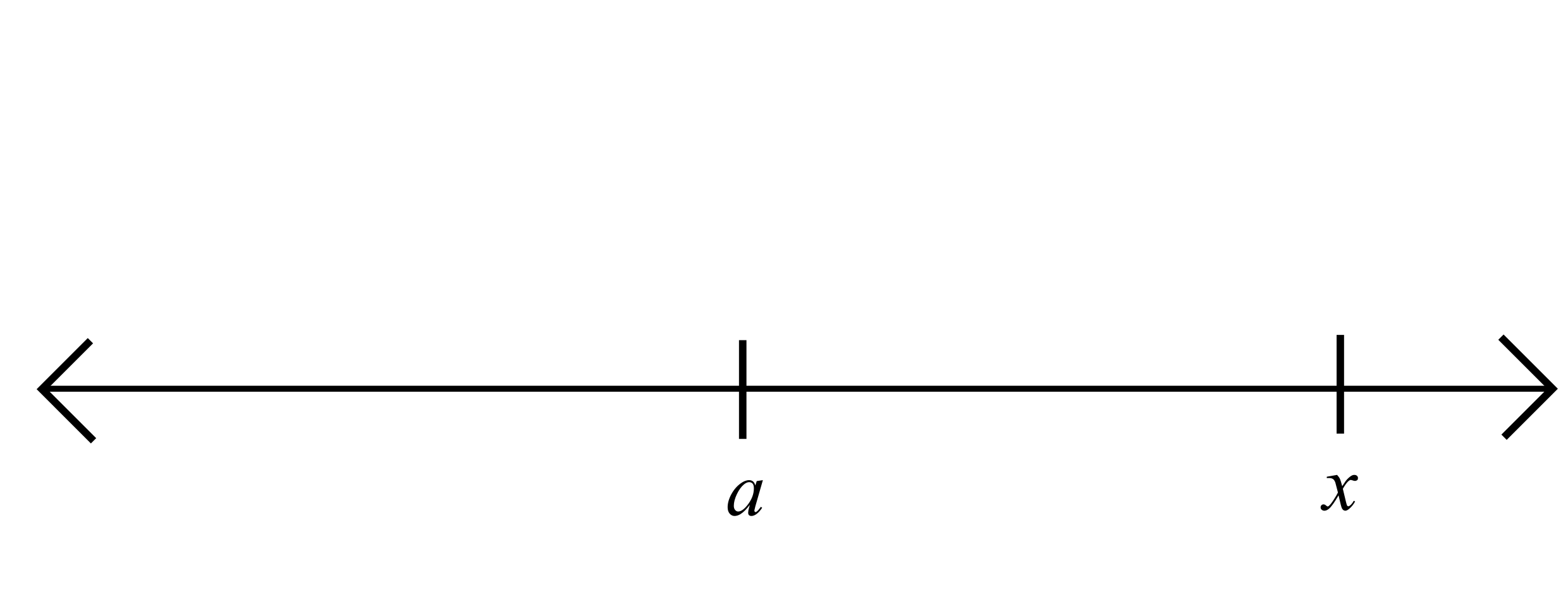
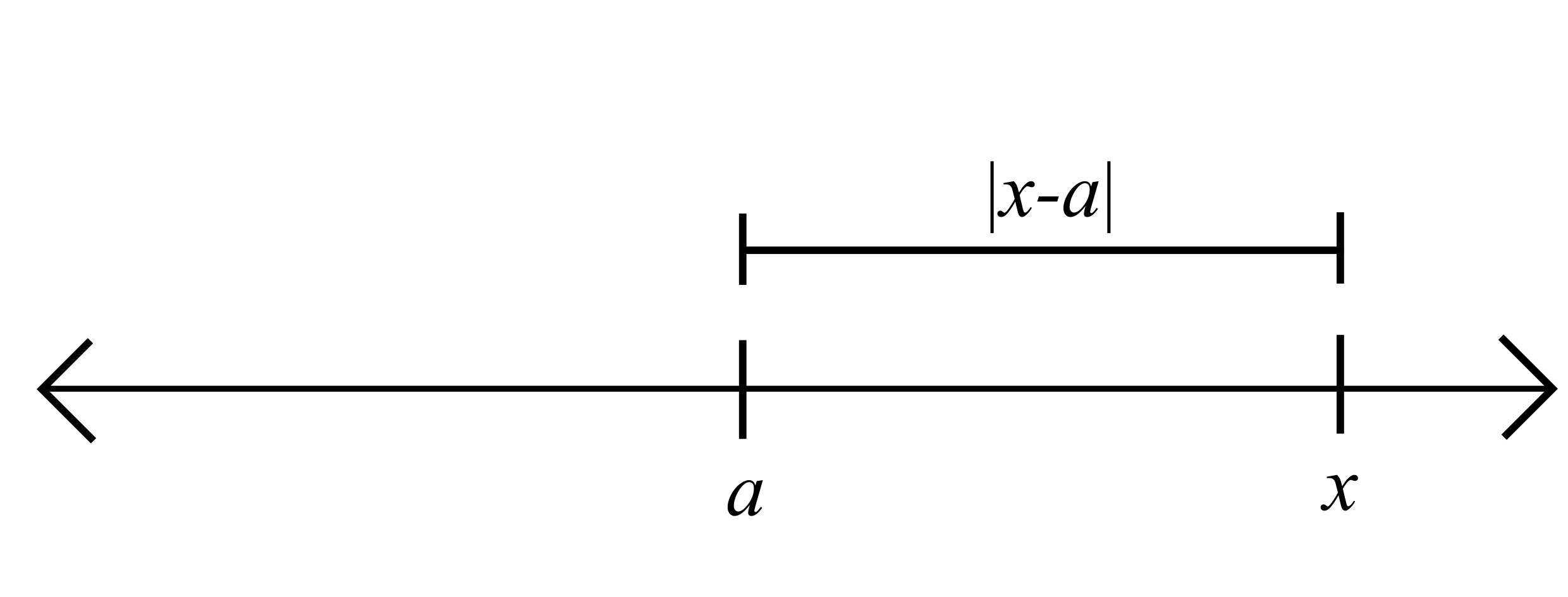
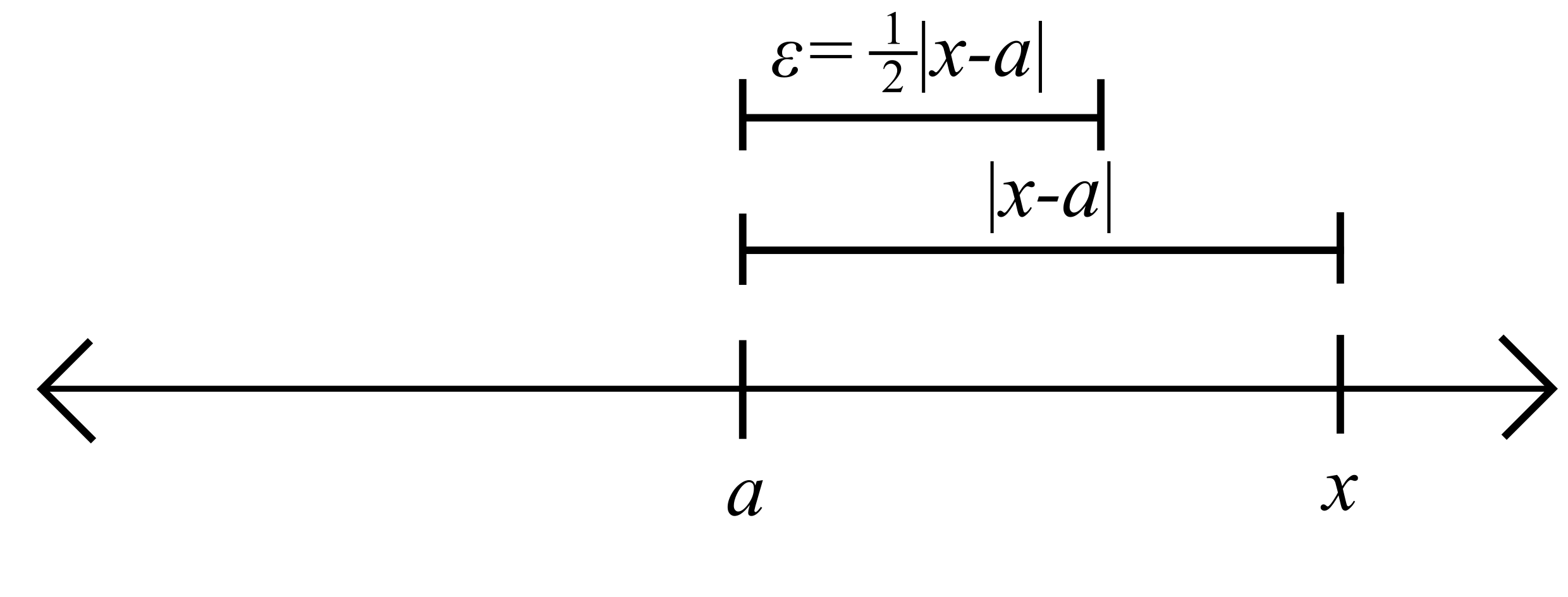
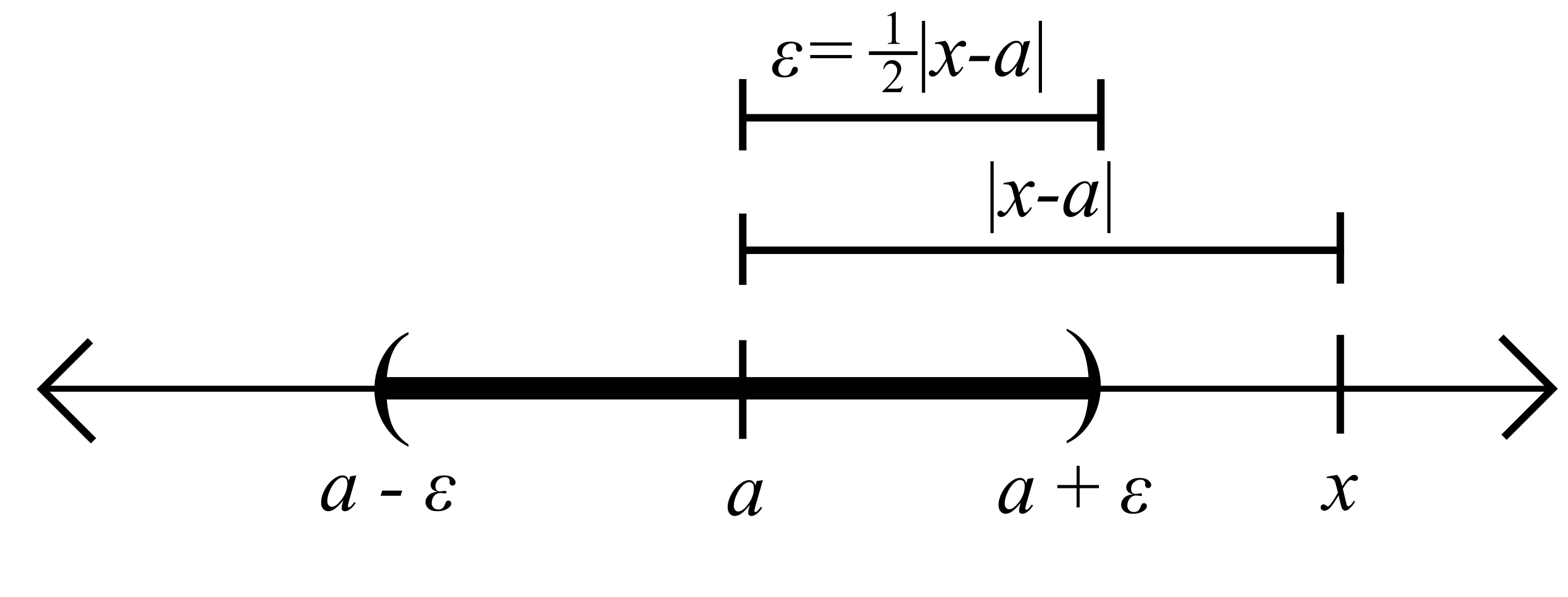
With this choice of \(\varepsilon\), it appears from the picture that \(x\notin V_{\varepsilon}(a)\).
Proof. We will prove this by contrapositive. Assume \(x\neq a\). Set
\[\varepsilon = \frac{1}{2}|x-a|.\]
Since \(x\neq a\), we see that \(\varepsilon>0\). To complete the proof, we note that
\[|x-a|>\frac{1}{2}|x-a| = \varepsilon,\]
and therefore \(x\notin V_{\varepsilon}(a)\). \(\Box\)
Theorem 2.2.8. Let \(a\) and \(x\) be real number. If \(x\in V_{\varepsilon}(a)\) for all \(\varepsilon>0\), then \(x=a\).
Proposition. Let \(a\) and \(b\) be real numbers, and let \(\varepsilon>0\).
If \(V_{\varepsilon}(a)\cap V_{\varepsilon}(b) = \varnothing\), then \(|a-b|\geq 2\varepsilon\).
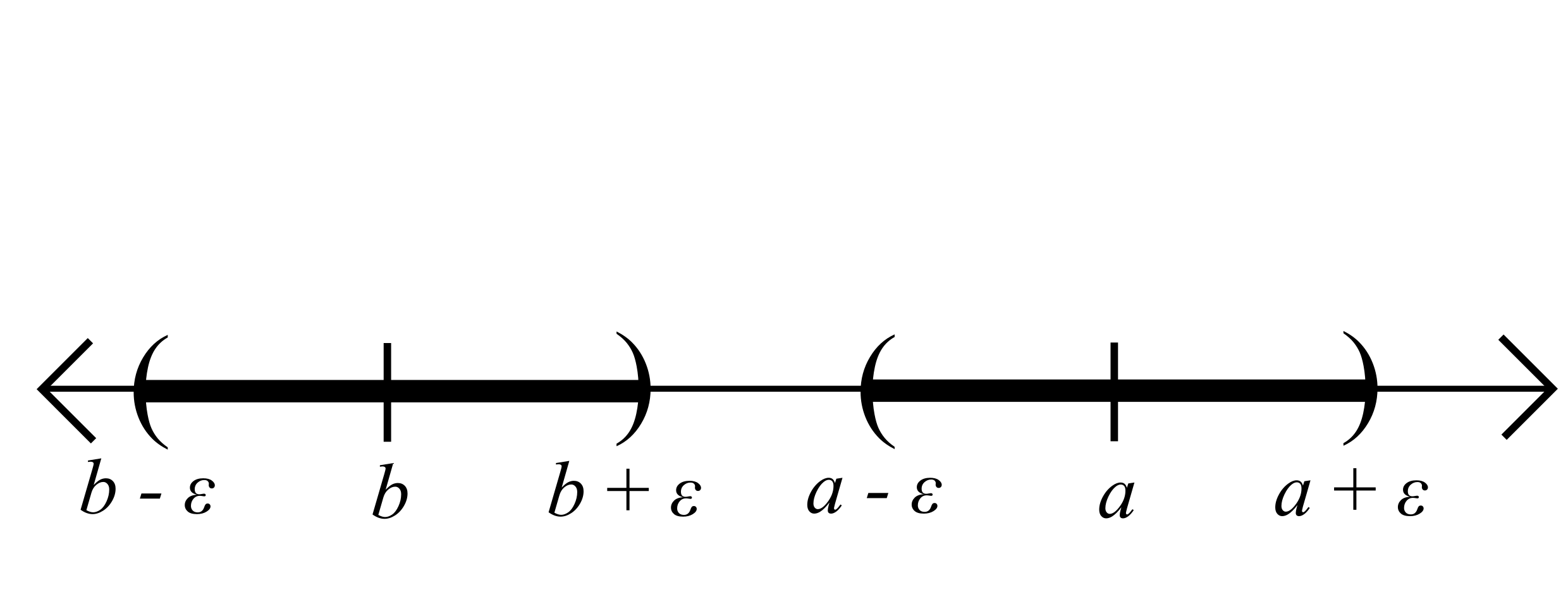
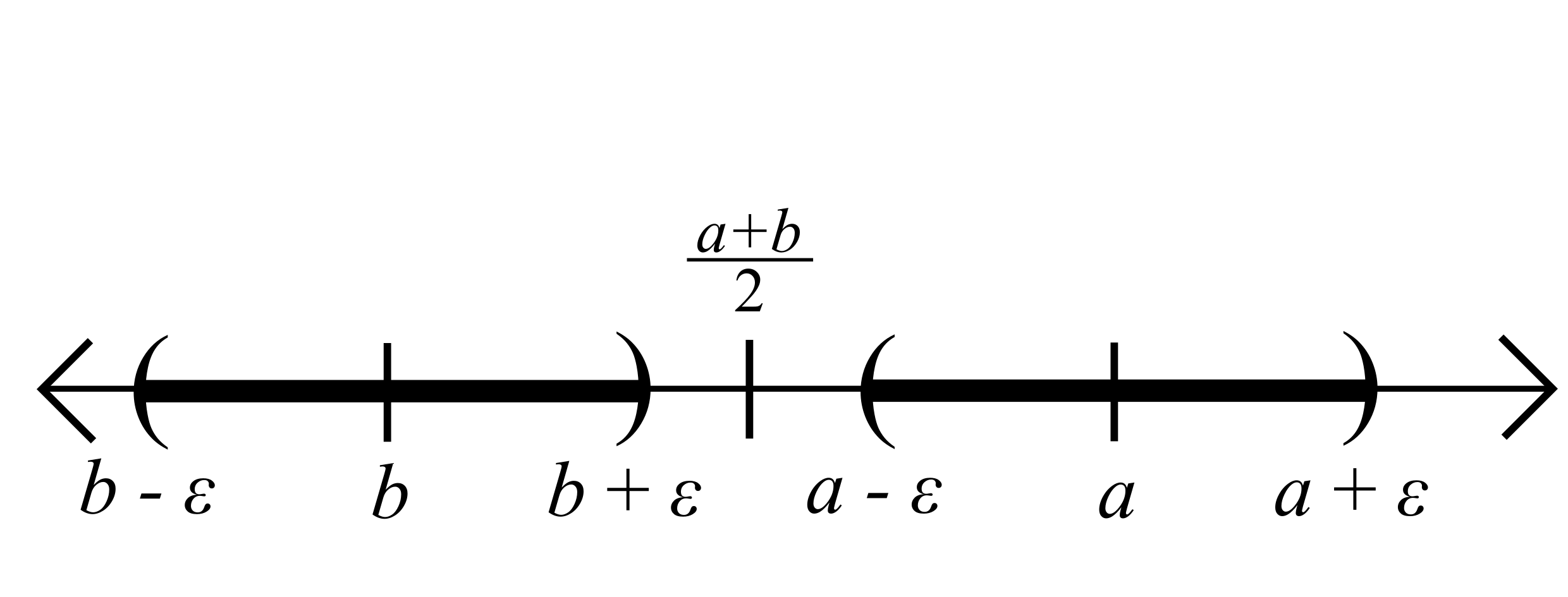
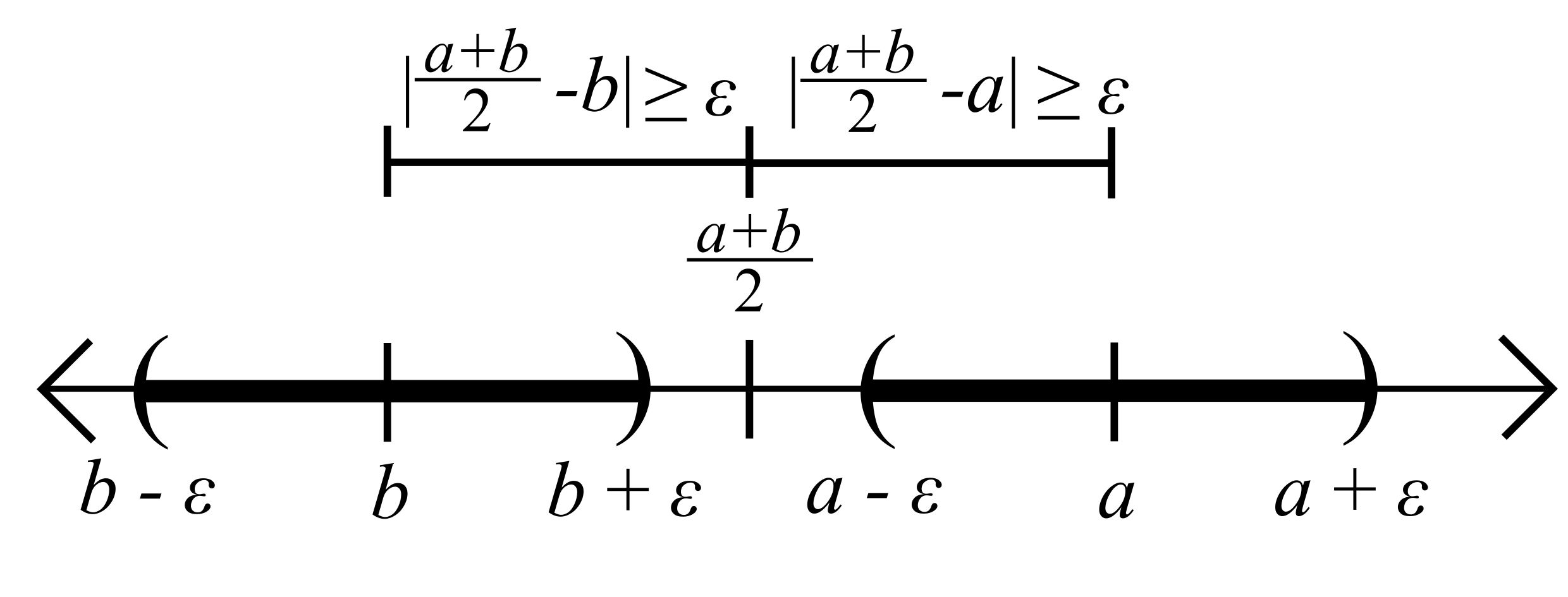
Proposition. Let \(a\) and \(b\) be real numbers, and let \(\varepsilon>0\).
If \(V_{\varepsilon}(a)\cap V_{\varepsilon}(b) = \varnothing\), then \(|a-b|\geq 2\varepsilon\).
Proof. Assume \(V_{\varepsilon}(a)\cap V_{\varepsilon}(b) = \varnothing\). Set
\[c = \frac{a+b}{2}.\]
Note that
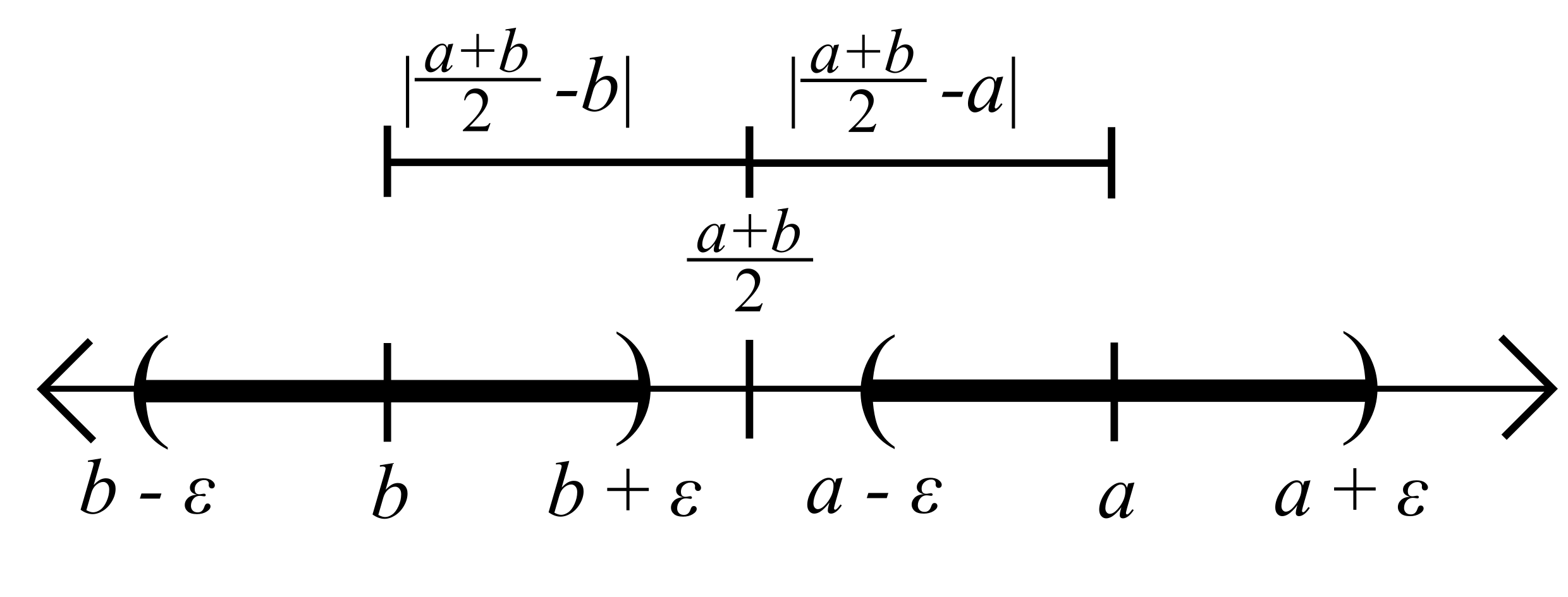
\[|a-c| = \left|a-\frac{a+b}{2}\right| = \left|\frac{a-b}{2}\right| = \frac{1}{2}|a-b|,\]
and
\[|b-c| = \left|b-\frac{a+b}{2}\right| = \left|\frac{b-a}{2}\right| = \frac{1}{2}|a-b|.\]
Since \(c\) is not in both \(V_{\varepsilon}(a)\) and \(V_{\varepsilon}(b)\), it must be the case that either \(|a-c|\geq \varepsilon\) or \(|b-c|\geq \varepsilon\). In either case this implies \[\frac{1}{2}|a-b|\geq \varepsilon.\ \Box\]
Proposition. If \(a\neq b\), then there are numbers \(\varepsilon>0\) and \(\delta>0\) such that \(V_{\varepsilon}(a)\cap V_{\delta}(b) = \varnothing\).

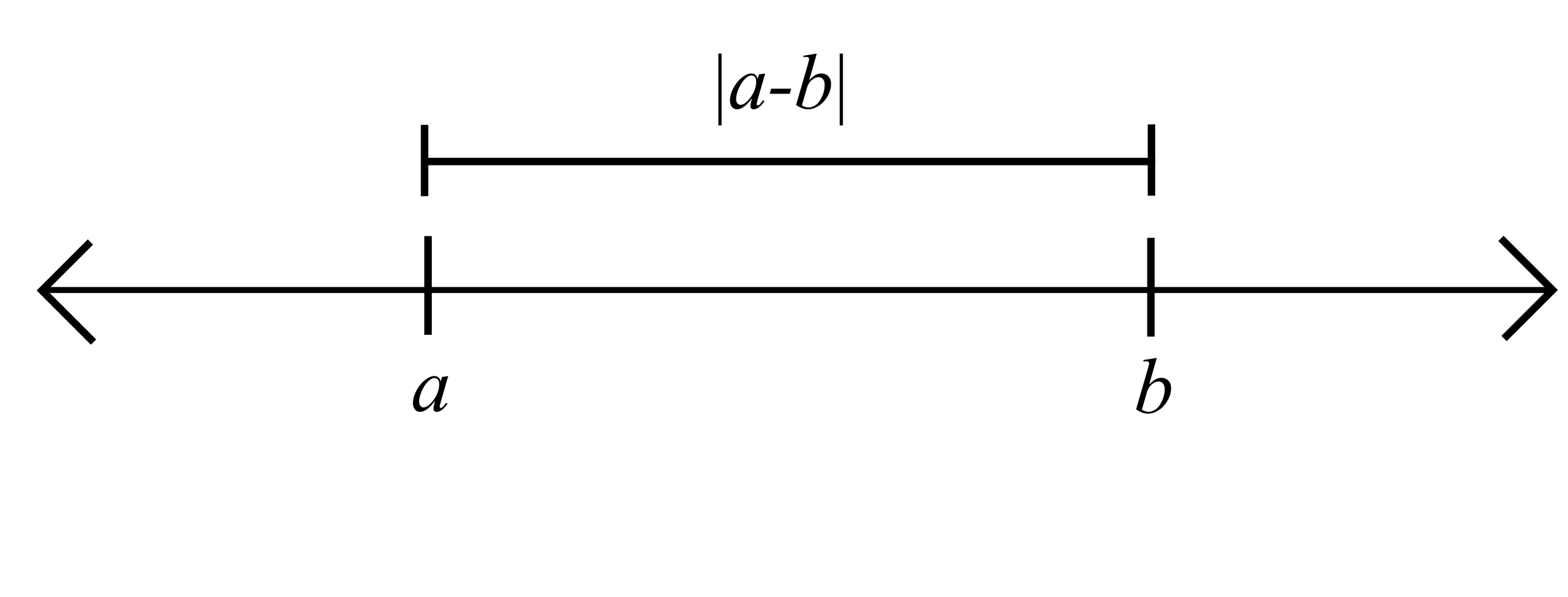
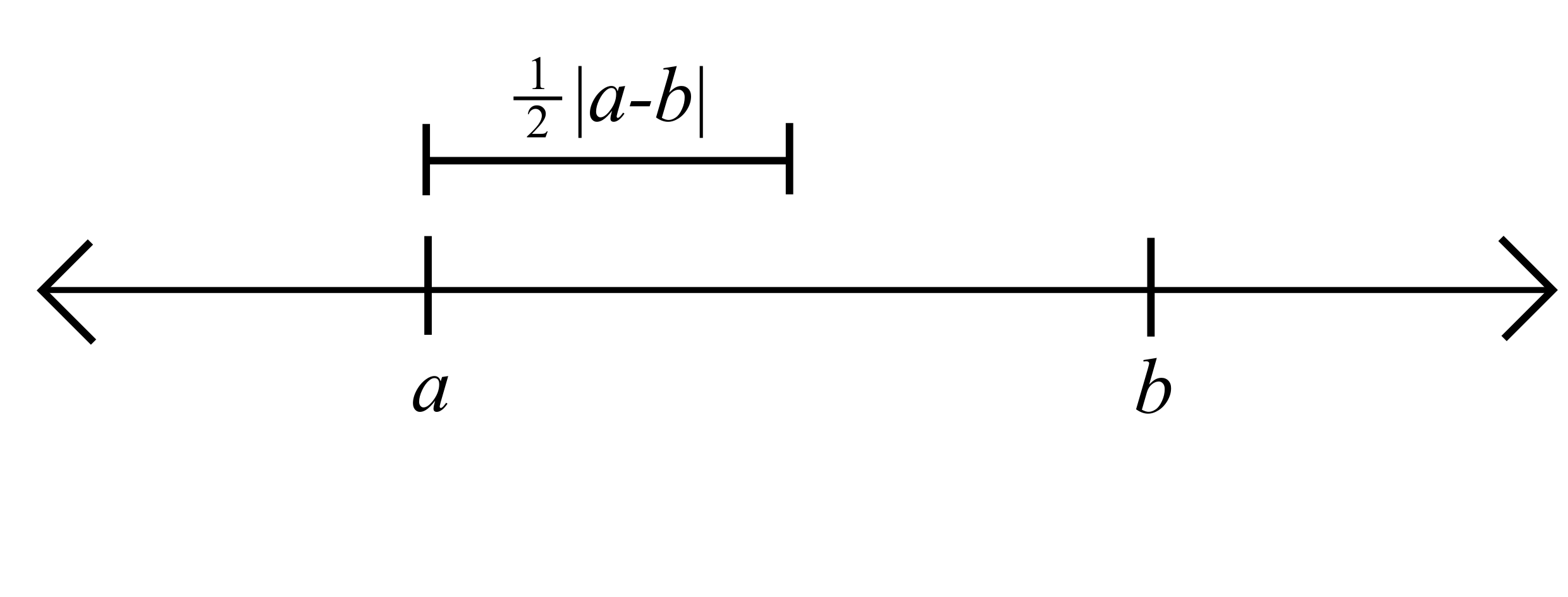
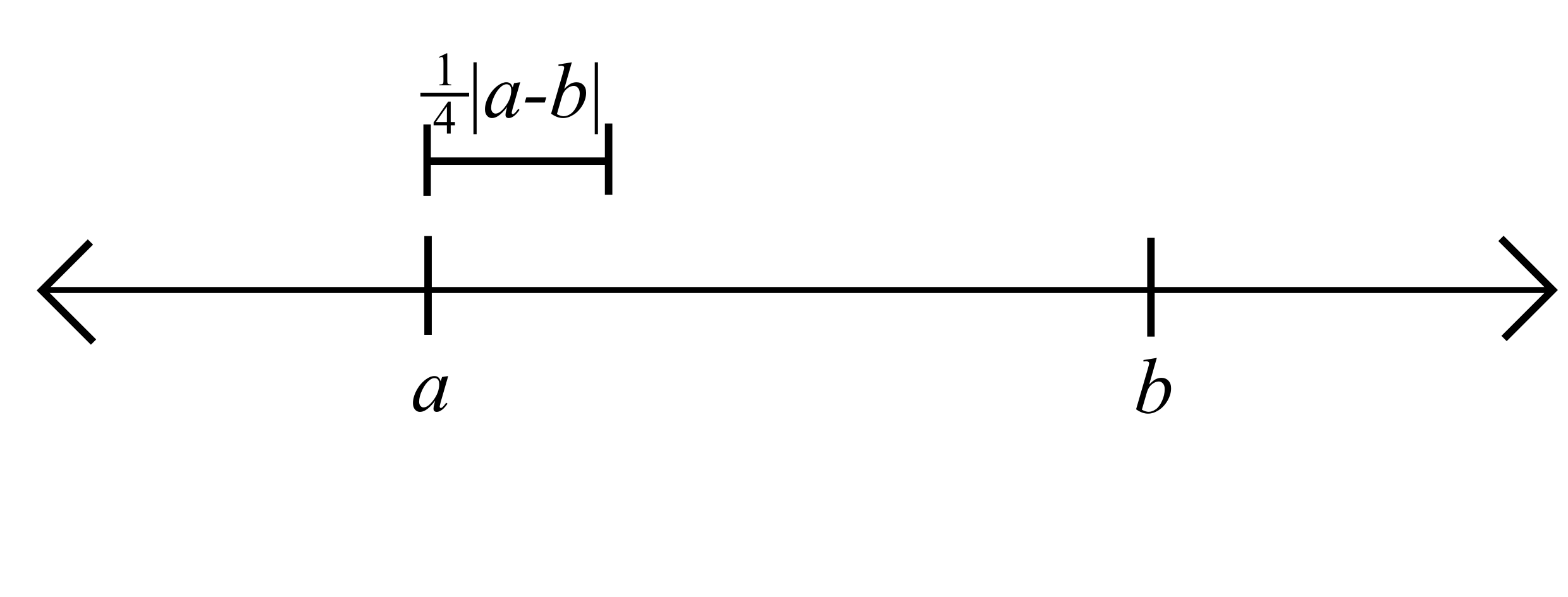
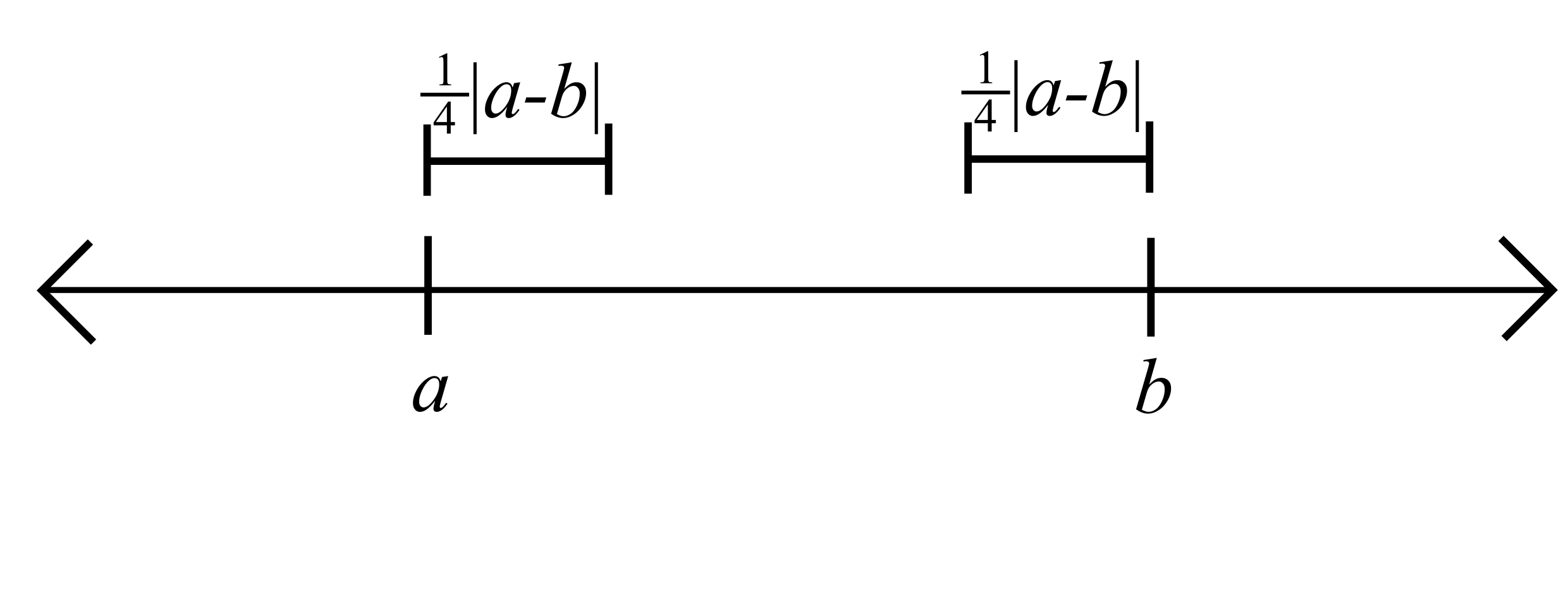
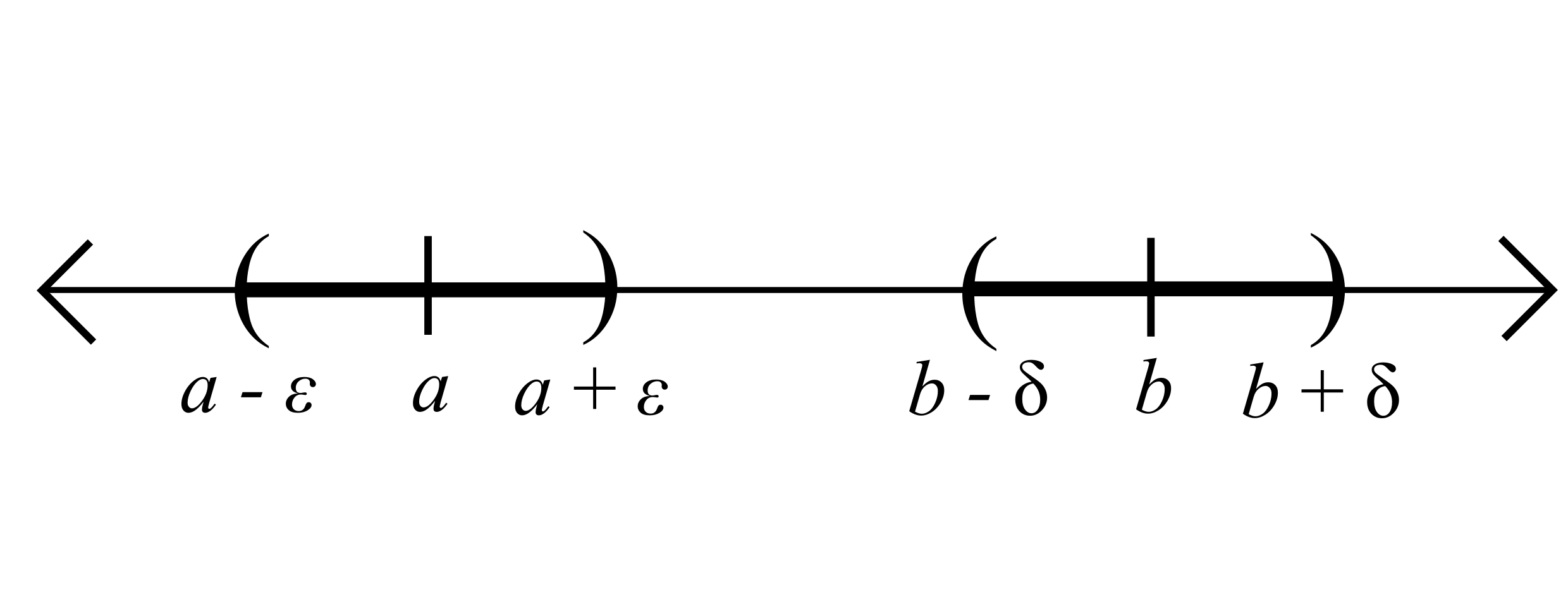
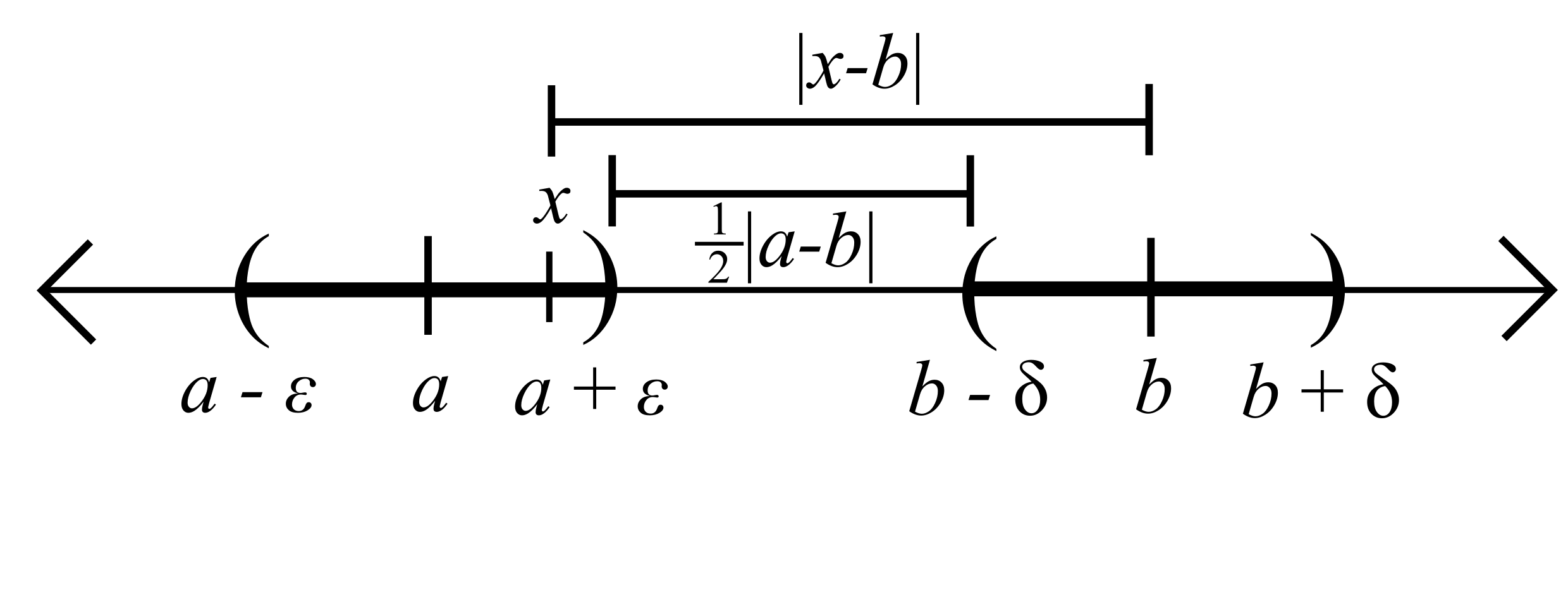
\(|x-b|>\frac{1}{2}|a-b|+\delta=\frac{3}{4}|a-b|>\delta\)
Take \(\varepsilon = \frac{1}{4}|a-b|\) and \(\delta = \frac{1}{4}|a-b|\)
Proposition. If \(a\neq b\), then there are numbers \(\varepsilon>0\) and \(\delta>0\) such that \(V_{\varepsilon}(a)\cap V_{\delta}(b) = \varnothing\).
Proof. Suppose \(a\) and \(b\) are real numbers with \(a\neq b\). Since \(a\neq b\) we have \(|a-b|>0\). Set
\[\varepsilon=\delta=\frac{1}{4}|a-b|.\]
Clearly \(\varepsilon>0\) and \(\delta>0\). We claim that \(V_{\varepsilon}(a)\cap V_{\delta}(b) = \varnothing\).
Suppose \(x\in V_{\varepsilon}(a)\). By definition \(|x-a|<\varepsilon\), which implies \[-|x-a|>-\varepsilon.\] By the reverse triangle inequalty
\[|x-b| = |(a-b)+(x-a)|\geq |a-b|-|x-a|\]
Hence, \(x\notin V_{\delta}(b)\). \(\Box\)
\[>|a-b|-\varepsilon = \frac{3}{4}|a-b|>\delta.\]
Practice problem:
Prove the last proposition, but with \(\varepsilon=\delta=\frac{1}{2}|a-b|\).
End Lecture 8
Read Section 2.3
Proof. Suppose \(a\) and \(b\) are real numbers with \(a\neq b\). Since \(a\neq b\) we have \(|a-b|>0\). Set
\[\varepsilon=\delta=\frac{1}{2}|a-b|.\]
Clearly \(\varepsilon>0\) and \(\delta>0\). We claim that \(V_{\varepsilon}(a)\cap V_{\delta}(b) = \varnothing\).
Suppose \(x\in V_{\varepsilon}(a)\). By definition \(|x-a|<\varepsilon\), which implies \[-|x-a|>-\varepsilon.\] By the reverse triangle inequalty
\[|x-b| = |(a-b)+(x-a)|\geq |a-b|-|x-a|\]
Hence, \(x\notin V_{\delta}(b)\). \(\Box\)
\[>|a-b|-\varepsilon = \frac{1}{2}|a-b|=\delta.\]
End Lecture 8
Lecture 8
By John Jasper
Lecture 8
- 227



