Bewijzen en redeneren voor informatici
Oefenzitting 3: Bewijzen
Basisconcepten
- Bewijs door vaststelling (e.g. waarheidstabel)
- Bewijs door constructie
bv. er bestaat een x waarvoor P(x), geef simpelweg een voorbeeld - Bewijs door tekening (e.g. venn diagram)
- Substitutie, gebruik definities, modus ponens
modus ponens \( A \Rightarrow B \) is waar en \(A \) is waar dan is \( B \) waar zijn - Ketens van (on)gelijkheden, implicaties en equivalenties
bv. toon aan dat \( A \Leftrightarrow B \): \( A \Leftrightarrow \dots \Leftrightarrow \dots \Leftrightarrow B \)
Basisconcepten
- Wederzijdse implicatie
\( A \Leftrightarrow B \) asa \( A \Rightarrow B \wedge B \Rightarrow A \) - Inclusie van verzamelingen
\( A \subseteq B \) asa \(\forall x \in A: x \in B\) - Gelijkheid van verzamelingen
\(A = B \) asa \( A \subseteq B \wedge B \subseteq A\) - Gevalsonderscheid
- Bewijs uit het ongerijmde
Om \(P\) te bewijzen bewijs dat \(\neg P \) een contradictie is - Bewijs door inductie: inductiebasis, inductiestap
Oefening 4.12
Keten van gelijkheden, substitutie

Oefening 4.14
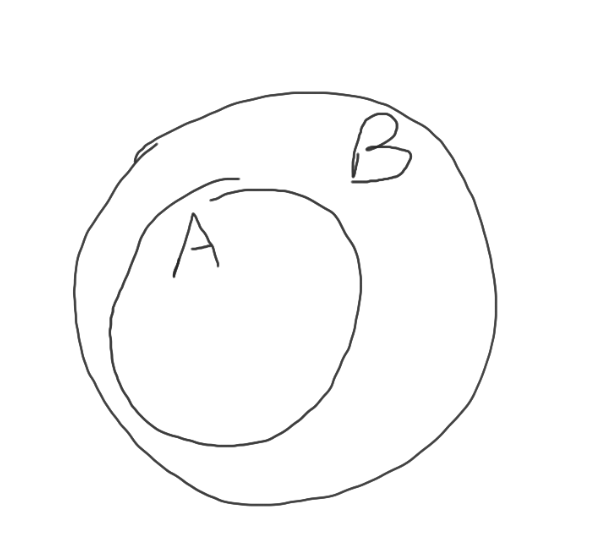
Wederzijdse implicatie, bewijs adhv tekening
TB: \( A \subseteq B \Leftrightarrow A \cup B = B \)
\( A \subseteq B \Rightarrow A \cup B = B \)
Oefening 4.14
Wederzijdse implicatie, inclusie en gelijkheid van verzamelingen, substitutie
TB: \( A \subseteq B \Leftrightarrow A \cup B = B \)
\( A \cup B = B \Rightarrow A \subseteq B \)
Gegeven: \( \forall x: x\in A \vee x \in B \Leftrightarrow x \in B \)
Te bewijzen: \( \forall y: y \in A \Rightarrow x \in B \)
- Neem een willekeurige \( y \in A \)
- Deze \(y \in A\) en is er voldaan aan \(y \in A \vee y \in B \)
- Dus volgens het gegeven is \( y \in B \) waar
Oefening 4.22
Bewijs uit het ongerijmde

Je neemt de negatie van het verkeerde
Beschouw een niet vlakke graaf met minder dan 5 knopen
bri-2021-04
By Jonas Soenen
bri-2021-04
BRI Exercise Lecture 01
- 1,234


