Flag Hilbert–Poincaré series & related zeta functions
Joshua Maglione
Otto von Guericke Universität Magdeburg
math.uni-bielefeld.de/~jmaglione
www.slides.com/joshmaglione/lincoln-lund
Joint with ...
Igusa's zeta functions
Count roots of \(f\in\Z[X_1,\dots, X_d]\) modulo an integer. Fix prime \(p\).
N_m(p) = \#\left\{X\in(\Z/p^m\Z)^d ~\middle|~ f(X)\equiv 0\mod p^m\right\}
Goal: understand asymptotics of
\displaystyle P_f(T) = \sum_{m=0}^\infty \dfrac{N_m(p)}{p^{dm}}T^m
Disguised \(p\)-adic integral \(Z_f(s)\) in complex variable \(s\):
P_f(p^{-s}) = \dfrac{1 - p^{-s} Z_f(s)}{1 - p^{-s}}
counting
measure
Igusa's zeta
function
Thm (Igusa 1974). Functions \(Z_f(s)\) and \(P_f(T)\) are rational in \(p^{-s}\) and \(T\), respectively.
Key step in proof: Hironaka's resolution of singularities.
Leaves open many questions:
- How can we compute these?
- What are the asymptotics?
Of interest to us: products of linear polynomials.
Zero locus yields a hyperplane arrangement.
Igusa zeta functions arise when computing subgroup, representation, and class-counting zeta functions.
Goal: use combinatorial & topological tools to understand asymptotics and arithmetic of the Igusa zeta function \(Z_f(s)\).
\displaystyle f(\bm{X}) = \prod_{k=1}^m L_k(\bm{X})
\deg(L_k) = 1
Bigger Picture:
\mathsf{fHP}_{\mathcal{A}}
Z_f^{\mathrm{mot}}
Z_f
\zeta_G^{\mathrm{cc}}
Z_f^{\mathrm{top}}
\mathsf{cfHP}_{\mathcal{A}}
\left\{\phantom{\displaystyle\sum} \right.
Flag Hilbert–Poincaré series
Hyperplane arrangement \(\mathcal{A}\) finite set of hyperplanes in \(K^d\).
Intersection poset: ordered by reverse inclusion
\mathcal{L}(\mathcal{A}) = \left\{\bigcap_{H\in S} H ~\middle|~ S\subseteq \mathcal{A} \right\}.
- Bottom element \(\hat{0}\) : the affine space \(K^d\).
- Top element \(\hat{1}\) : the common intersection (if exists).
If \(\hat{1}\in\mathcal{L}(\mathcal{A})\), then \(\mathcal{A}\) is central.
\pi_{\mathcal{A}}(Y) = \displaystyle\sum_{x\in\mathcal{L}(\mathcal{A})} \mu(\hat{0},x)(-Y)^{\mathrm{rk}(x)} = \mathrm{Poin}(\mathbb{C}^d \setminus \bigcup_{H\in\mathcal{A}}H;\; Y)
Poincaré polynomial:
\(K\!=\!\mathbb{C}\)
Coefficients are Betti numbers.
Example.
\mathsf{A}_n := \{X_i - X_j ~|~ 1 \leqslant i < j \leqslant n+1\}.
\pi_{\mathsf{A}_3}(Y) = 1 + 6Y + 11Y^2 + 6Y^3
\(\mathrm{rk}\)
0
1
2
3
\(\mathcal{L}(\mathsf{A}_3)\)
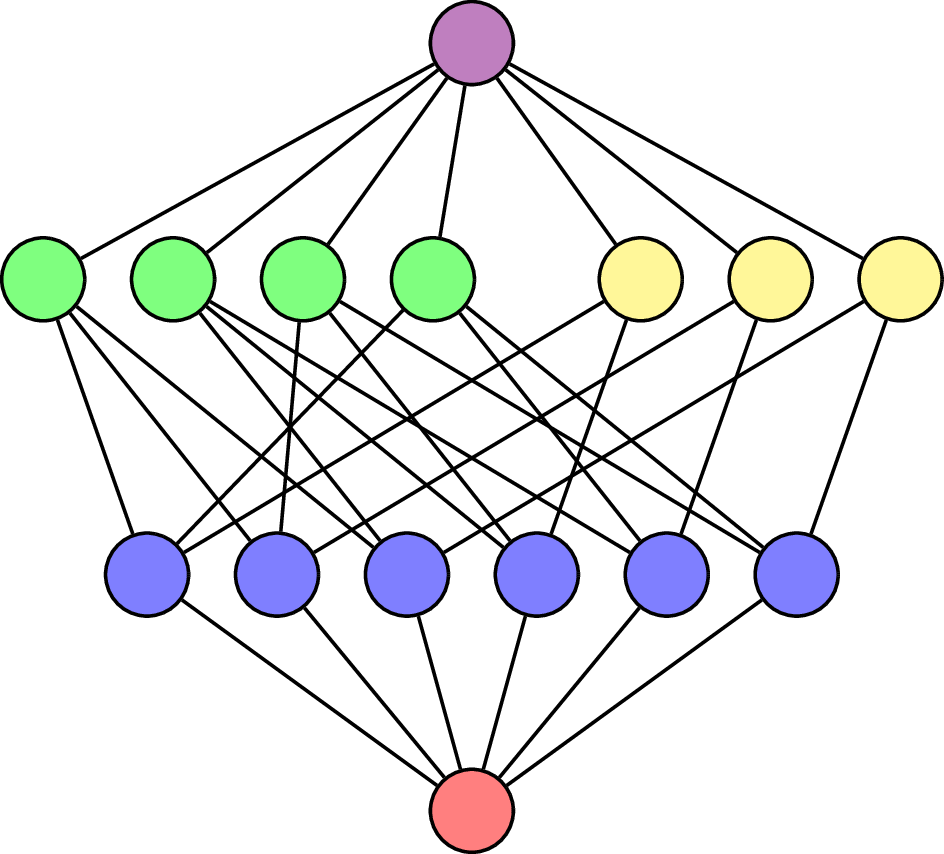
\(\hat{0}\)
\(\hat{1}\)
\(\mathsf{A}_3\)
With \(x\in \mathcal{L}(\mathcal{A})\), two new arrangements
\begin{aligned}
\mathcal{A}_x &= \left\{H\in\mathcal{A} ~\middle|~ x\subseteq H \right\}, & & (\text{localization})\\
\mathcal{A}^x &= \left\{x\cap H ~\middle|~ H\in\mathcal{A}\setminus\mathcal{A}_x,\; x\cap H\neq \varnothing \right\}. & & (\text{restriction})
\end{aligned}
Order complex: \(\Delta(\mathcal{L}(\mathcal{A}))\) set of flags in \(\mathcal{L}(\mathcal{A})\).
In \(\mathcal{A}_x\): \(x\) is now \(\hat{1}\). In \(\mathcal{A}^x\): \(x\) is now \(\hat{0}\).
For \(F = (x_1 < \cdots < x_\ell)\in\Delta(\mathcal{L}(\mathcal{A}))\), with \(x_0=\hat{0}\), \(x_{\ell+1}=\varnothing\),
\pi_F(Y) = \displaystyle\prod_{k=0}^{\ell} \pi_{\mathcal{A}^{x_k}_{x_{k+1}}}(Y).
Flag Poincaré polynomials.
Interval \([x_k, x_{k+1}]\)
in \(\mathcal{L}(\mathcal{A})\)
Example: \(\mathcal{A} = \mathsf{A}_3\).
\(F\) empty flag in \(\Delta(\mathcal{L}(\mathcal{A}))\):
\begin{aligned}
\pi_F(Y) &= \pi_{\mathcal{A}_{\varnothing}^{\hat{0}}}(Y) = \pi_{\mathcal{A}}(Y) \\
&= 1 + 6Y + 11Y^2 + 6Y^3
\end{aligned}
For \(F = (x_1 < \cdots < x_\ell)\in\Delta(\mathcal{L}(\mathcal{A}))\), with \(x_0=\hat{0}\), \(x_{\ell+1}=\varnothing\),
\pi_F(Y) = \displaystyle\prod_{k=0}^{\ell} \pi_{\mathcal{A}^{x_k}_{x_{k+1}}}(Y).
\(F = (\quad\;)\):
\begin{aligned}
\pi_F(Y) &= \pi_{\mathcal{A}^{\hat{0}}}(Y) \cdot\pi_{\mathcal{A}_{\varnothing}}(Y) \\
&= (1+Y)\cdot (1 + 3Y + 2Y^2)
\end{aligned}
\begin{aligned}
\pi_F(Y) &= \pi_{\mathcal{A}^{\hat{0}}}(Y) \cdot \pi_{\mathcal{A}_{\phantom{-}}}(Y) \cdot \pi_{\mathcal{A}_{\varnothing}}(Y) \\
&= (1+Y)\cdot (1 + Y) \cdot (1 + Y)
\end{aligned}
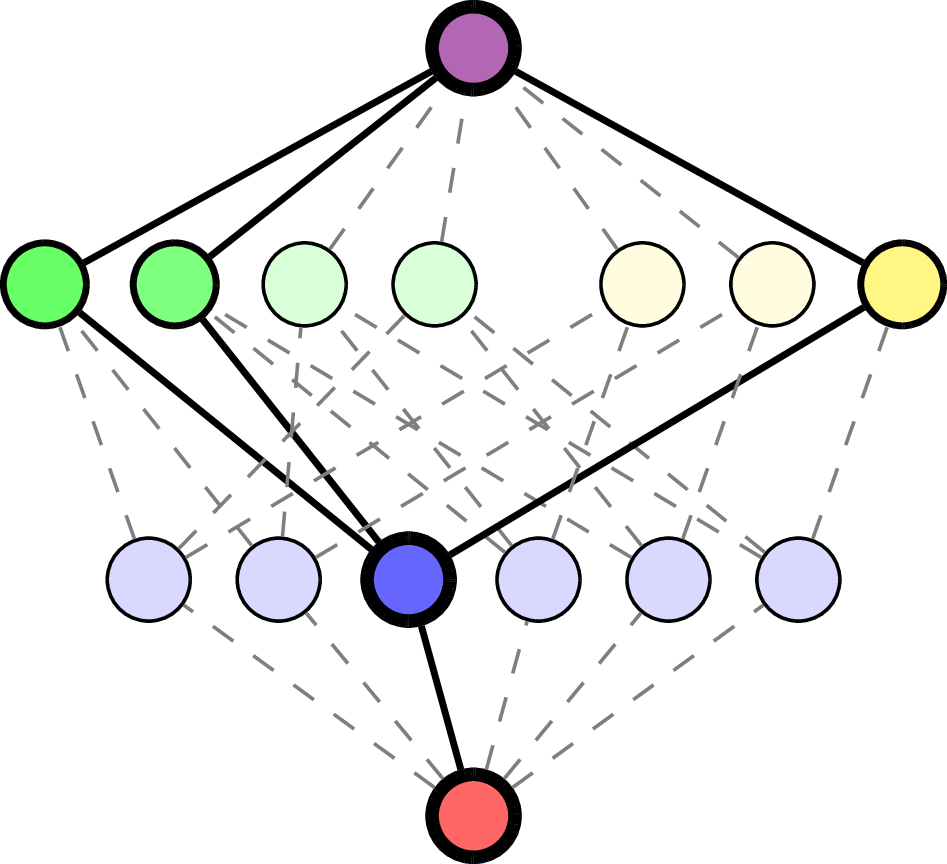
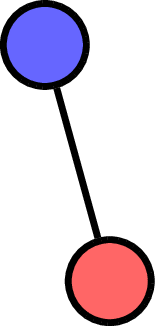
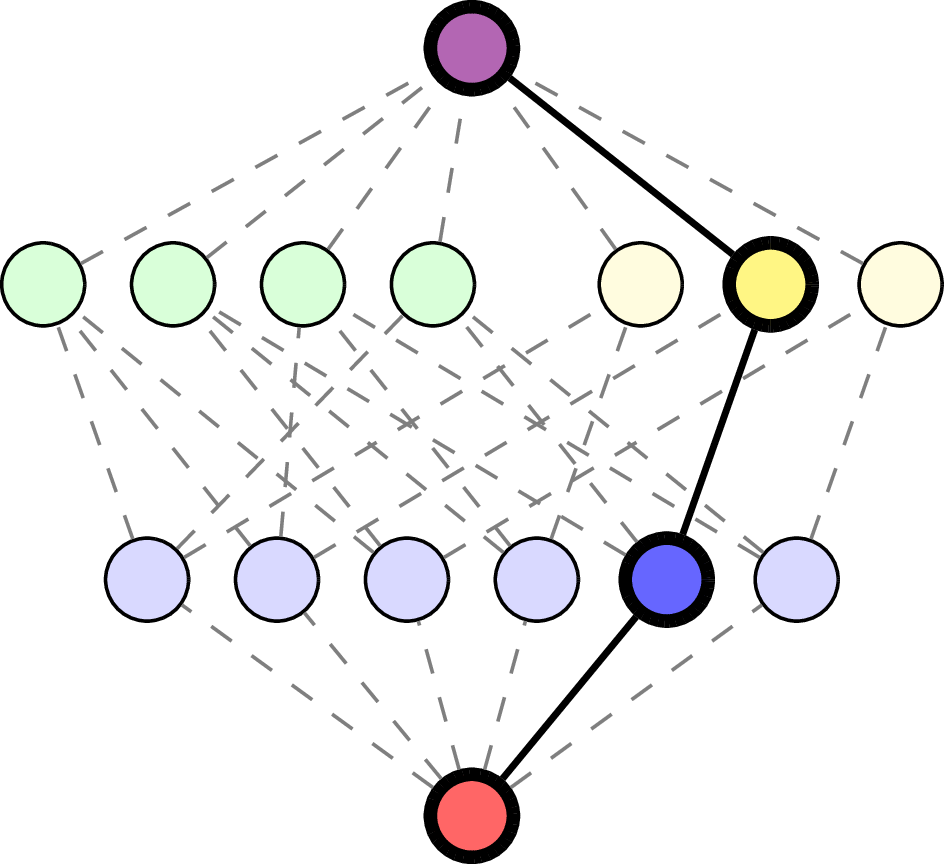
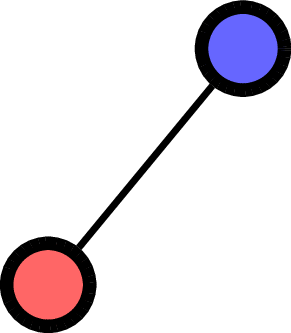
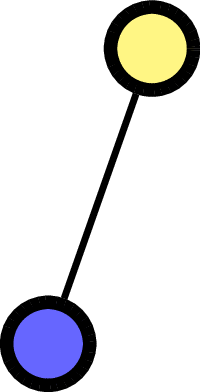
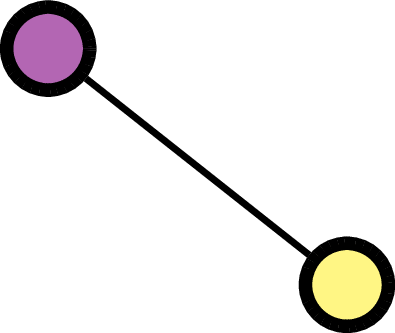
\(F = (\quad\;<\;\quad)\):
Self reciprocity
Set \(\widetilde{\mathcal{L}}(\mathcal{A}) = \mathcal{L}(\mathcal{A})\setminus\{\hat{0}\}\). The flag Hilbert–Poincaré series:
\mathsf{fHP}_{\mathcal{A}}(Y, \bm{T}) = \displaystyle\sum_{F\in\Delta(\widetilde{\mathcal{L}}(\mathcal{A}))} \pi_F(Y) \prod_{x\in F} \dfrac{T_x}{1 - T_x}
Thm (M.–Voll 2021). For \(\mathcal{A}\) defined over characteristic \(0\) field and central, then
\mathsf{fHP}_{\mathcal{A}}\left(Y^{-1},(T_x^{-1})_{x\in\widetilde{\mathcal{L}}(\mathcal{A})}\right) = (-Y)^{-\mathrm{rk}(\mathcal{A})} T_{\hat{1}} \cdot \mathsf{fHP}_{\mathcal{A}}(Y, \bm{T}).
Idea: \(\mathsf{fHP}_{\mathcal{A}}\) is equivalent to a multivariate \(p\)-adic integral.
Connections to zeta functions
Let \(K\) be a number field and \(\mathcal{O}_K\) its ring of integers.
Assume \(\mathfrak{o}\) is a compact discrete valuation ring, and
- \(\mathfrak{o}\) is an \(\mathcal{O}_K\)-module,
- \(\mathfrak{p}\) is its maximal ideal,
- \(\mathbb{F}_q \cong \mathfrak{o}/\mathfrak{p}\).
Write \(\mathcal{A}(\mathfrak{o})\) for set of linear polynomials in \(\mathcal{O}_K[X_1,\dots, X_d]\) representing the (abstract) arrangement \(\mathcal{A}\).
Say \(\mathcal{A}(\mathfrak{o})\) has good reduction over \(\mathbb{F}_q\) if
\mathcal{L}(\mathcal{A}(\mathfrak{o})) \cong \mathcal{L}(\mathcal{A}(\mathfrak{o}/\mathfrak{p})).
is the Igusa zeta function associated to \(\mathcal{A}(\mathfrak{o})\).
\mathsf{fHP}_{\mathcal{A}}\left(-q^{-1}, (q^{-\mathrm{rk}(x) - \lambda_x s})_{x\in\widetilde{\mathcal{L}}(\mathcal{A})}\right)
Thm (M.–Voll 2021). If \(\mathcal{A}\) defined over \(K\) with good reduction over \(\mathbb{F}_q\), then
For \(x\in\mathcal{L}(\mathcal{A})\), set
\lambda_x = \# \left\{ H\in\mathcal{A} ~\middle|~ x\subseteq H \right\}.
Note: a similar multivariate substitution holds, yielding another substitution to certain class-counting zeta functions.
We see all of the candidate poles coming from combinatorial data.
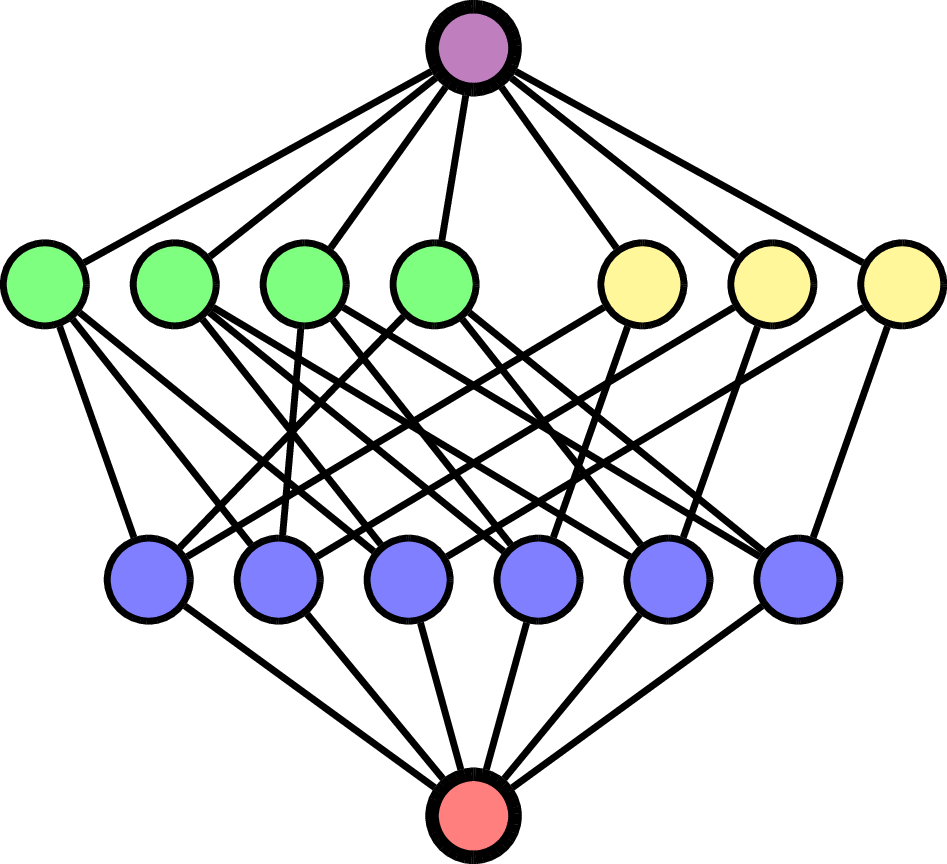
\(\mathcal{L}(\mathsf{A}_3)\)
Igusa zeta function associated to
\begin{aligned}
Y &= -p^{-1}, \\
T_x &= \begin{cases}
p^{-1-s} & x = \phantom{-}, \\
p^{-2-2s} & x = \phantom{-}, \\
p^{-2-3s} & x = \phantom{-}, \\
p^{-3-6s} & x = \phantom{-}.
\end{cases}
\end{aligned}
\dfrac{(1-p^{-1})\left(1 - 5p^{-1} + 6p^{-2} + \cdots - 6p^{-4-5s} + 5p^{-5-5s} - p^{-6-5s}\right)}{(1 - p^{-1-s})^2(1 - p^{-2-3s})(1 - p^{-3-6s})}
Igusa zeta function of \(f_{\mathsf{A}_3}\): for all primes \(p\),
f_{\mathsf{A}_3}(\bm{X}) = (X_1 - X_2)(X_1 - X_3)(X_1 - X_4)(X_2 - X_3)(X_2 - X_4)(X_3 - X_4)
Class counting zeta function
\zeta^{\mathrm{cc}}_{\mathbf{G}\otimes \mathbb{Z}_p}(s) = \displaystyle \sum_{m=0}^{\infty} \# \mathrm{cc}(\mathbf{G}(\mathbb{Z}/p^m\mathbb{Z})) p^{-ms}
Let \(\mathbf{G}\) be a nilpotent group scheme of finite type over \(\mathbb{Z}\):
Set \(\Gamma = K_{3,2}\) and \(\mathbf{G}_{\Gamma}\) graphical group scheme.
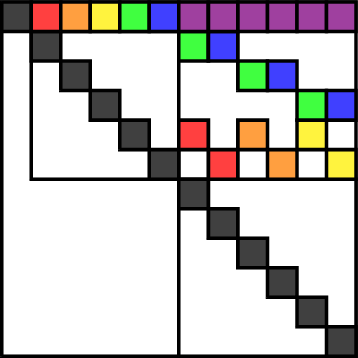
\(\mathbf{G}_{\Gamma}(\mathbb{Z}_p)\) =
\(\leqslant\mathrm{GL}_{12}(\mathbb{Z}_p)\)
\( =\langle I + E_{1,2} + E_{5,7} + E_{6,8},~\dots, \)
\( I + E_{1,6} - E_{2,8} - E_{3,10} - E_{4,12}\rangle\)
A graph \(\Gamma\) is a cograph if \(\Gamma\) contains no path on 4 vertices as an induced subgraph.
Let \(\mathcal{C}_n\) be the set of \(n\) coordinate hyperplanes in \(K^n\).
Thm (Rossmann–Voll 2019 + M.–Voll 2021). If \(\Gamma\) is a cograph on \(n\) vertices, then for all \(x\in\mathcal{L}(\mathcal{C}_{n+1})\) there exist polynomials \(f_x\) such that for all \(\mathfrak{o}\),
\zeta_{\mathbf{G}_{\Gamma}\otimes \mathfrak{o}}^{\mathrm{cc}}(s) = \mathsf{fHP}_{\mathcal{C}_{n+1}}\left(-q^{-1}, (q^{-f_x(s)})_{x\in\widetilde{\mathcal{L}}(\mathcal{C}_{n+1})} \right).
The polynomials are of the form
f_x(s) = \mu_x s + \nu_x,
for \(\mu_x\in\{0,1\}, \nu_x\in\mathbb{Z}\).
\(\mathcal{C}_n\) coordinate hyperplanes in \(K^n\) and \(\mathcal{L}(\mathcal{C}_n)\cong 2^{[n]}\).
\begin{aligned}
Y &= -p^{-1}, \\
T_I &= \begin{cases}
p^{6-|I|-s} & I = \phantom{-}, \\
p^{7-|I|-s} & I = \phantom{-}, \\
p^{8-|I|-s} & I = \phantom{-}, \\
p^{4-s} & I = \phantom{-}, \\
p^{-|I|} & I = \phantom{-}.
\end{cases}
\end{aligned}
Class counting zeta function for \(\mathbf{G}_{\Gamma}(\mathbb{Z}_p)\) for all primes \(p\):
\dfrac{1 + p^{-s} - p^{1-s} - 2p^{2-s} - p^{3-s} + p^{4-s} + p^{4-2s}}{(1-p^{3-s})(1-p^{5-s})^2}
Details: Rossmann–Voll
A different coarsening
Set each \(T_x=T\) to get coarse flag Hilbert–Poincaré series:
Easier to see examples & other combinatorial properties.
Nice form:
\mathsf{cfHP}_{\mathcal{A}}(Y, T) = \dfrac{\mathcal{N}_{\mathcal{A}}(Y, T)}{(1 - T)^{\mathrm{rk(\mathcal{A})}}}
\mathsf{cfHP}_{\mathcal{A}}(Y, T) = \displaystyle\sum_{F\in\Delta(\widetilde{\mathcal{L}}(\mathcal{A}))} \pi_F(Y) \left(\dfrac{T}{1 - T}\right)^{\# F}
\mathcal{N}_{\mathcal{A}}(Y, T) = \displaystyle\sum_{F\in\Delta(\widetilde{\mathcal{L}}(\mathcal{A}))} \pi_F(Y) T^{|F|}(1 - T)^{\mathrm{rk}(\mathcal{A})-|F|}
\mathcal{N}_{\mathsf{A}_1}(Y, T) = 1 + Y
\mathcal{N}_{\mathsf{A}_2}(Y, T) = 1 + 3Y + 2Y^2 + (2 + 3Y + Y^2)T
\begin{aligned}
\mathcal{N}_{\mathsf{A}_3}(Y, T) &= 1 + 6Y + 11Y^2 + 6Y^3 \\
&\quad + (11 + 37Y + 37Y^2 + 11Y^3)T \\
&\quad + (6 + 11Y + 6Y^2 + Y^3)T^2
\end{aligned}
All nonnegative coefficients. Computed with \(\mathsf{HypIgu}\).
Braid arrangement in \(\mathbb{Q}^{n+1}\):
\mathsf{A}_n = \{X_i - X_j ~|~ 1\leqslant i < j \leqslant n+1\}
SageMath
Do coefficients of \(\mathcal{N}_{\mathcal{A}}(Y, T)\) have combinatorial interpretation?
Conjecture (M.–Voll). For arbitrary \(\mathcal{A}\), the coefficients of \(\mathcal{N}_{\mathcal{A}}(Y, T)\) are nonnegative.
\mathsf{cfHP}_{\mathcal{A}}(Y, 0) = \pi_{\mathcal{A}}(Y)
\mathsf{cfHP}_{\mathcal{A}}(0, T) = \mathrm{Hilb}(\mathbb{Q}[\Delta]; T)
where
\mathbb{Q}[\Delta] \cong \mathbb{Q}\left[Z_x ~\middle|~ x\in\widetilde{\mathcal{L}}(\mathcal{A})\right]/\left(\prod_{x\in S}Z_x ~|~ S\subseteq\widetilde{\mathcal{L}}(\mathcal{A}) \text{ not a flag}\right).
This is the Stanley–Reisner ring associated to \(\Delta(\widetilde{\mathcal{L}}(\mathcal{A}))\).
Question: Is \(\mathsf{cfHP}_{\mathcal{A}}\) the Hilbert series of an \(\mathbb{N}^2\)-graded algebra?
Coxeter arrangements
The Eulerian polynomial \(E_n(T)\) is combinatorially defined.
\begin{array}{rcccccccccc}
E_1: &&&&&& 1 &&&& \\
E_2: &&&&& 1 && 1 &&& \\
E_3: &&&& 1 && 4 && 1 && \\
E_4: &&& 1 && 11 && 11 && 1 & \\
E_5: && 1 && 26 && 66 && 26 && 1
\end{array}
\mathcal{N}_{\mathcal{A}}(1, T) = \pi_{\mathcal{A}}(1) \cdot E_{\mathrm{rk}(\mathcal{A})}(T).
Thm (M.–Voll 2021). For a Coxeter arrangement \(\mathcal{A}\) with no \(\mathsf{E}_8\) factors:
Also related to numerators of Hilbert series of Stanley–Reisner rings of barycentric subdivisions of boundaries of simplexes.
Chambers of real arrangements
Assume \(K\subseteq \mathbb{R}\), so \(\mathcal{A}\) partitions \(\mathbb{R}^d\) into regions.
Say \(\mathcal{A}\) is simplicial if all chambers are simplicial cones.
\mathcal{N}_{\mathcal{A}}(1, T) \geqslant \pi_{\mathcal{A}}(1) \cdot E_{\mathrm{rk}(\mathcal{A})}(T).
Thm (Kühne–M. 2021). If \(\mathcal{A}\) is central and defined over \(\mathbb{R}\), then under coefficient-wise comparison:
Equality holds if and only if \(\mathcal{A}\) is simplicial.
Idea.
Zaslavsky's Theorem tells us that
\pi_{\mathcal{A}}(1) = \#\{\text{chambers of } \mathcal{A}\}.
\mathsf{cfHP}_{\mathcal{A}}(1, T) = \displaystyle\sum_{\mathcal{C} \text{ chamber}}\mathrm{Hilb}(R_{\mathcal{C}}; T).
where
Sum of Betti numbers of the complement of \(\mathcal{A}\) over \(\mathbb{C}\) is the number of connected components of the complement of \(\mathcal{A}\) over \(\mathbb{R}\).
This yields:
\(R_{\mathcal{C}}\) is the Stanley–Reisner ring of the barycentric subdivision of \(\partial \mathcal{C}\).
(Suggests \(\mathsf{cfHP}_{\mathcal{A}}(Y, T)\) is a "\(Y\)-twisted" version!)
Together with a deep result from Ehrenborg–Karu (2007) in algebraic combinatorics, for all chambers \(\mathcal{C}\),
h(\partial \mathcal{C}; T) \geqslant E_{\mathrm{rk}(\mathcal{A})}(T),
under coefficient-wise comparison, where
\dfrac{h(\partial \mathcal{C}; T)}{(1 - T)^{\mathrm{rk}(\mathcal{A})}} = \mathrm{Hilb}(R_{\mathcal{C}}; T).
Example. Four planes in \(\mathbb{R}^3\) in generic position.
8 cones over triangles and 6 cones over squares
\begin{aligned}
\mathcal{N}_{\mathcal{A}}(1, T) &= 8(1 + 4T + T^2) + 6(1 + 6T + T^2) \\
&< 14(1 + 6T + T^2).
\end{aligned}
Conjecture (Kühne–M. 2021). For \(\mathcal{A}\) of rank \(r\geqslant 3\) over arbitrary fields \(K\),
(1 + T)^{r-1} < \dfrac{\mathcal{N}_{\mathcal{A}}(1, T)}{\pi_{\mathcal{A}}(1)} < E_{\mathrm{rk}(\mathcal{A})}^{\mathsf{B}}(T).
When \(K=\mathbb{R}\), this means the average chamber of \(\mathcal{A}\) is "between" a simplicial cone and a cubical cone.
Thm (Kühne–M. 2021). The conjecture holds for \(r=3\) and \((r, K)=(4,\mathbb{R})\). If the conjecture holds, then the bounds are sharp.
Type \(\mathsf{B}\) Eulerian polynomial, \(E_r^{\mathsf{B}}(T)\), similar to type \(\mathsf{A}\).
Numerators of Stanley–Reisner rings of barycentric subdivisions of boundaries of hypercubes.
Summary
Flag Hilbert–Poincaré series shows combinatorial features of
- Igusa zeta functions of products of linear polynomials,
- class-counting zeta functions of nilpotent "cographical" groups.
Thm. \(\mathcal{A}\) central and characteristic \(0\) \(\implies\) \(\mathsf{fHP}_{\mathcal{A}}\) self-reciprocal.
Conj. \(\mathcal{N}_{\mathcal{A}}(Y, T)\) has nonnegative coefficients.
Thm. \(\mathcal{A}\) over \(\mathbb{R}\) and simplicial \(\implies\) \(\mathcal{N}_{\mathcal{A}}(1, T)=\pi_{\mathcal{A}}(1)\cdot E_{\mathrm{rk}(\mathcal{A})}(T)\).
Flag Hilbert-Poincaré series & related zeta functions
By Josh Maglione
Flag Hilbert-Poincaré series & related zeta functions
We define a class of multivariate rational functions associated with hyperplane arrangements called flag Hilbert-Poincaré series. We show how these rational functions are connected to Igusa zeta functions and class counting zeta functions for certain graphical group schemes studied by Rossmann and Voll. We report on a general self-reciprocity result and explore other connections within algebraic combinatorics. This is joint work with Christopher Voll and with Lukas Kühne.
