CPSC 359: Tutorial 1
Introduction
PhD Student
Fall 2018
Introduction
Joshua Horacsek (PhD Student)
joshua.horacsek@ucalgary.ca
MS 625A
http://cpsc.ucalgary.ca/~joshua.horacsek/
Policy:
- No food or drink
- Be academically honest
- Be respectful of your peers
I don't have office hours, but I'll meet on request
Tutorial Structure
Generally, I try to create tutorial material so that it prepares students for assignments.
Example exercises, help sessions, additional complimentary material
Boolean Functions
\(f=x+y\cdot z\)
The goal of this tutorial is to get you familliar with boolean functions, i.e.
| x | y | z | yz | f |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Eventually, we'll look at how to design boolean functions to solve problems
Boolean Functions
\(f=x+y\cdot z\)
The goal of this tutorial is to get you familliar with boolean functions, i.e.
\(x\)
\(z\)
\(y\)
\(f\)
We'll look at a couple of these as examples
Exercises
\(f=x\cdot y+x^\prime\cdot y\)
Create the truth table and logic diagram for the following boolean function
Exercises
\(f=xy^\prime z+xy^\prime z^\prime\)
Create the truth table and logic diagram for the following boolean function
Exercises
\(f=xy^\prime+wz\)
Create the truth table and logic diagram for the following boolean function
Algebraic Simplification
There are many benefits to simplifying a boolean function, for example
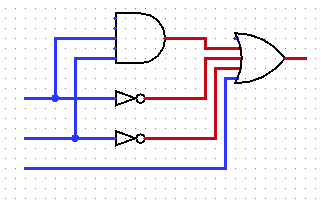
\(x\)
\(y\)
\(z\)
This function actually does nothing...
Algebraic Simplification
There are many benefits to simplifying a boolean function, for example
\(f=x+y^\prime+z^\prime+yz\)
We'll look more at this next day...
CPSC 359: Tutorial 1
By Joshua Horacsek
CPSC 359: Tutorial 1
- 1,549



