Practical non-Cartesian Computing
(for Scientific Visualization)
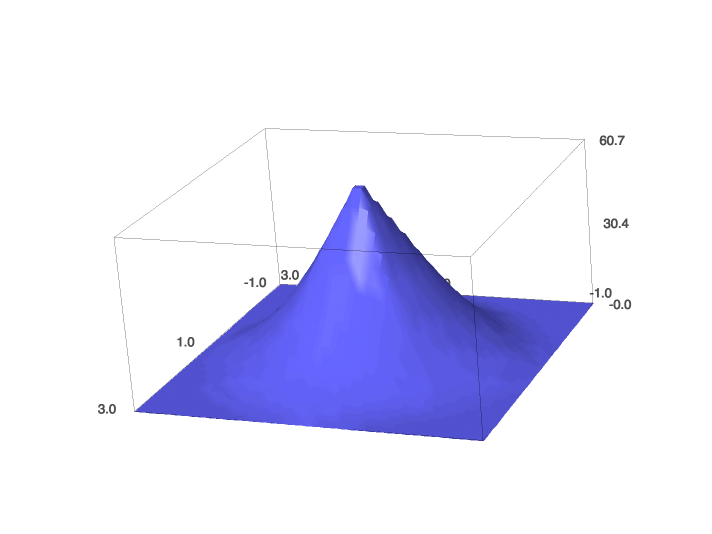
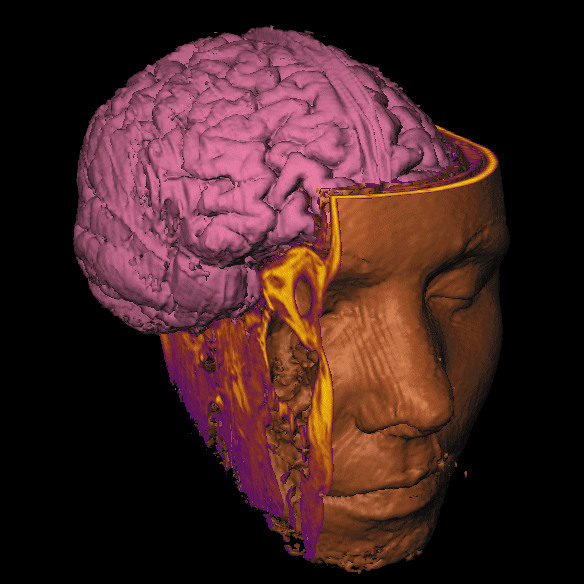
Scientific Visualization
Attempt to communicate a message about data through images
Practically speaking, this thesis work has grown beyond scientific visualization.
Non Cartesian Computing
If an application uses a regular grid for simulation, then there is a high probability that it's a Cartesian grid.
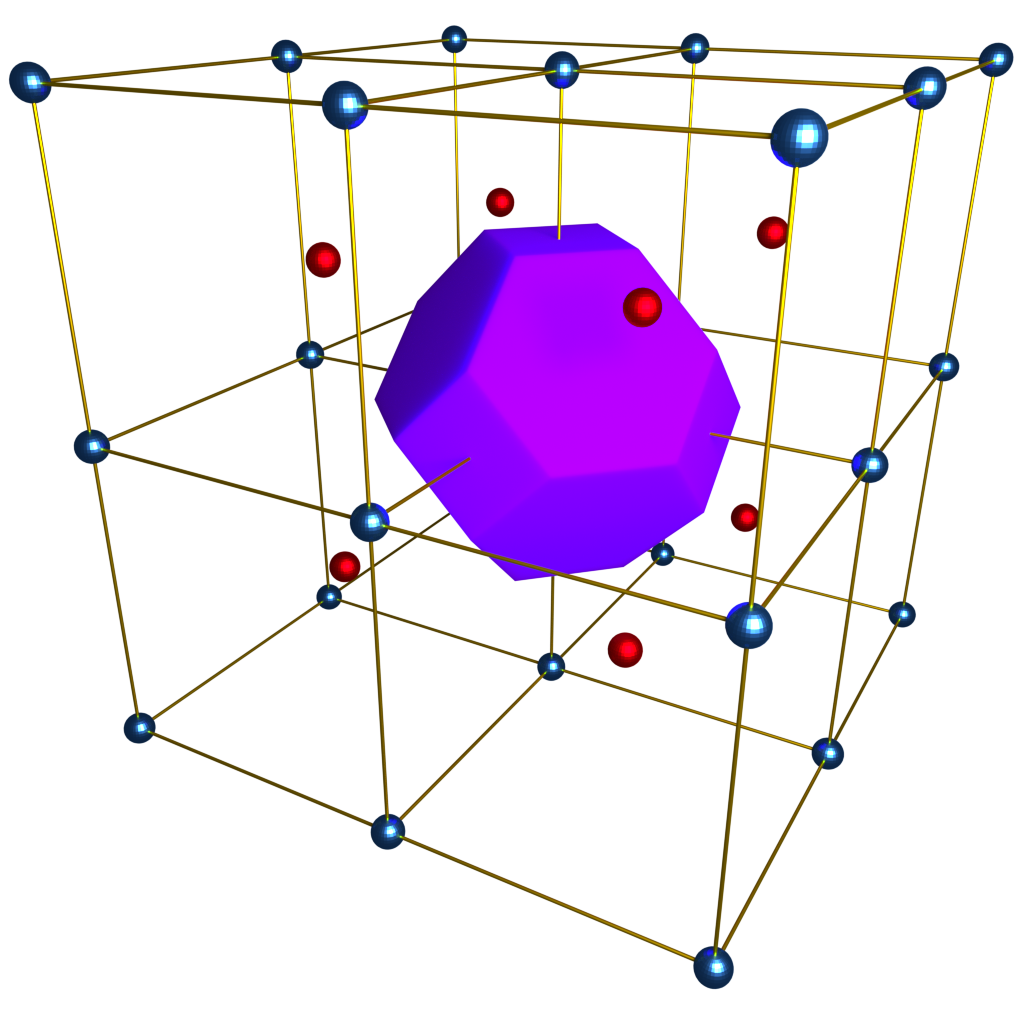
Cartesian
Body Centered Cubic
Face Centered Cubic
Non Cartesian Computing
Why use a non-Cartesian grid? Higher approximation capacity, more isotropic, better simulation results [1]
Cartesian
Body Centered Cubic
Face Centered Cubic
Challenges?
What are the challenges?
There are many! But I'll focus on a few fundamental ones related to Scientific Visualization that I tackle in my thesis work
- Challenge 1: Representation
- Challenge 2: Data Processing
- Challenge 3: Practicality
- Challenge 4: Usability
What are the challenges?
Challenge 1: Representation
How does one represent data on a non-Cartesian lattice? What's an appropriate data-structure?
- Transform the domain (a)
- Pretend the input is cartesian (b)
- Separate into cosets (c)
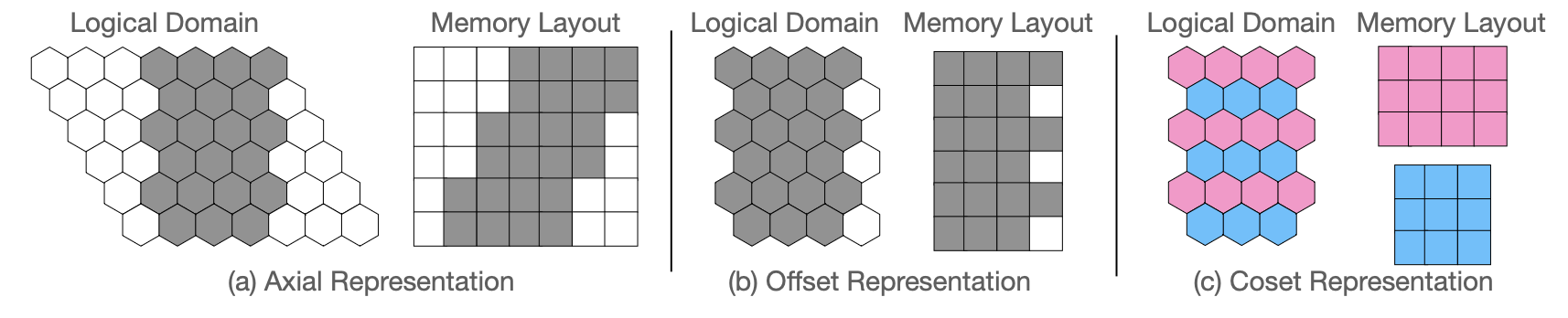
Note: Every integer lattice has a Cartesian coset decomposition.
What are the challenges?
Challenge 1: Representation
We introduce the lattice tensor data-structure.
- This data structure wastes no space in its representation (however does use a few bytes for auxiliary )
- Is practical for lattices used in image/volume processing
- Requires no "hacks" to support data processing on non-Cartesian lattice
- The base data-structure is very simple
Many algorithms can be extended to easily support this data-structure (convolution, Fourier transform, etc...)
Horacsek, Joshua, and Usman Alim. "NCDL: Non-Cartesian Deep Learning ", Submitted to NeurIPS 2023.
What are the challenges?
Challenge 2: Data Processing
Algorithms need to be extended for data-processing on non-Cartesian grids. Most algorithms are simple to re-state on non-Cartesian grids (convolution, padding, interpolation, attention, etc...) However, in practice their formulation and/or implementation can get quite involved.
Horacsek, Joshua, and Usman Alim. "NCDL: Non-Cartesian Deep Learning ", Submitted to NeurIPS 2023.
Horacsek, Joshua, and Usman Alim. "A closed PP form of box splines via Green’s function decomposition." Journal of Approximation Theory 233 (2018): 37-57.
What are the challenges?
Challenge 2: Data Processing
One of the more involved (and important in scientific visualization) techniques is interpolation.
Scientific visualization algorithms often require smooth input functions. The question is then, given an interpolant, designed for non-Cartesian data, how does one perform interpolation in a general and performant fashion?
Background:
- Many different papers investigate using specific box splines as interpolants [2,3,4,5,6].
- Some propose alternative spline structures (i.e. Voronoi splines) [7].
Box Splines?
\Xi = \begin{bmatrix}
| & | & \ & | \\
\xi_1 & \xi_2 & ... & \xi_n \\
| & | & \ & |
\end{bmatrix}.
Box splines are defined by an \(s\) by \(n\) matrix
And have the associated functional
M_\Xi(x) = \displaystyle\int_0^1M_{\Xi\backslash\xi}(x - t\xi) dt \text{ \ with \ } M_{[]}(x) := \delta(x)
Interpolant
Box-Splines
Typically evaluated via
M_\Xi(x) = \displaystyle\sum_{(\gamma,p)\in S_\Xi} \sum_{(\lambda, \alpha) \in P_{n-s}} \gamma\lambda |\det\Xi_\alpha|^{-1}{{[\![ (\Xi_\alpha^{-1}x) - p ]\!]}_{+}}^{\mu_\alpha - 1}
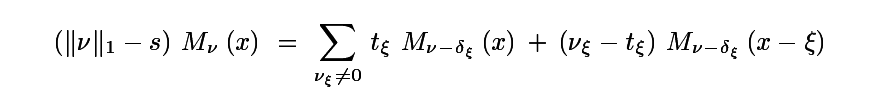
Our contribution is an explicit form for box-splines
Not exactly "easy" or "fast", but characterization is nice.
Horacsek, Joshua, and Usman Alim. "A closed PP form of box splines via Green’s function decomposition." Journal of Approximation Theory 233 (2018): 37-57.
What are the challenges?
Challenge 3: Practicality
Much of the work presented so far has been theoretical. That is, it answers the question of existence and provides construction methods, but they say little about the performance of those methods.
What are the challenges?
Challenge 3: Practicality
Research question:
Is there an overarching technique that can be generalized from the cases and techniques that have appeared so far in the literature?
\(\sum_{\mathbf{n}\in L\mathbb{Z}^s}c_{\mathbf{n}}\varphi\left(\frac{\mathbf{x}}{h}-\mathbf{n}\right)\)
Again, we focus on inperolation
What are the challenges?
Challenge 3: Practicality
For a given lattice/basis function combination, generate fast code for that combination?
We preform an in-depth symmetry analysis.
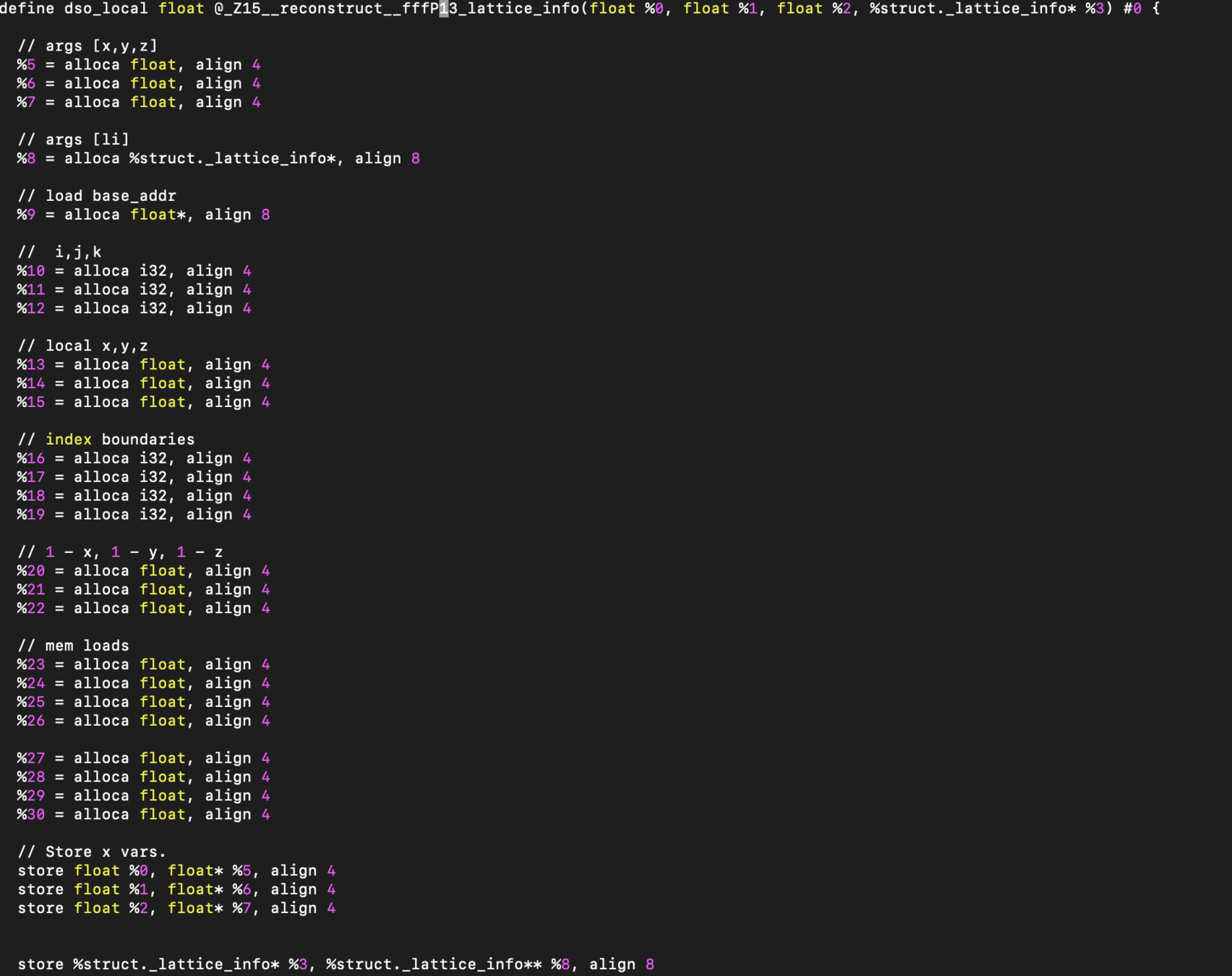
We then generate LLVM-IR (a low level code for a virtual machine that compiles to almost any modern compute architecture)
What are the challenges?
Challenge 3: Practicality
For a given lattice/basis function combination, generate fast code for that combination.
Horacsek, Joshua, and Usman Alim. "FastSpline: Automatic Generation of Interpolants for Lattice Samplings" ACM Transactions on Mathematical SoftwareVolume, 49 Issue 2 pp 1–35, https://doi.org/10.1145/3577194
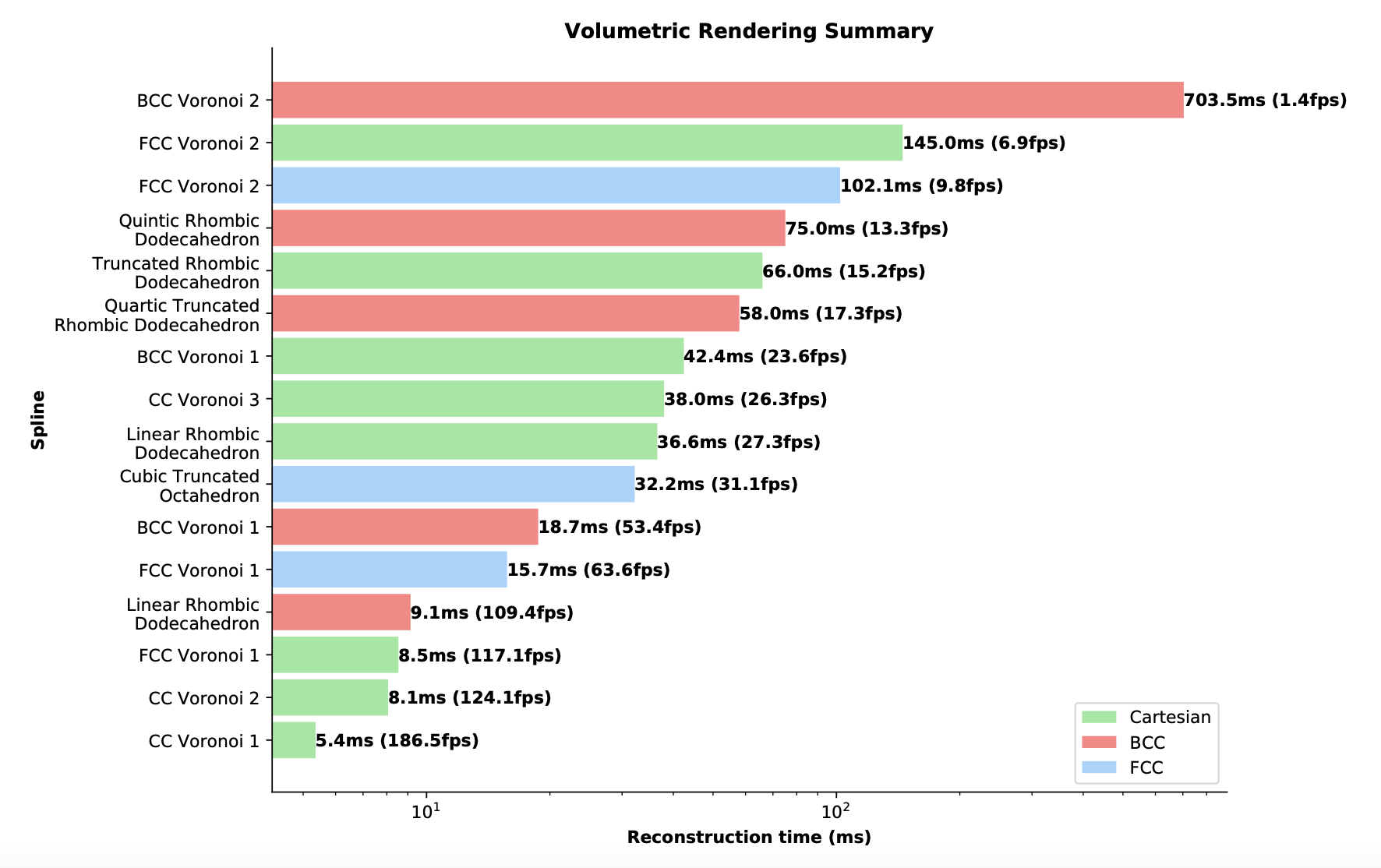
What are the challenges?
Challenge 3: Practicality
We also leverage fast algorithms on Cartesian lattices to build algorithms for non-Cartesian lattices (in a general setting).
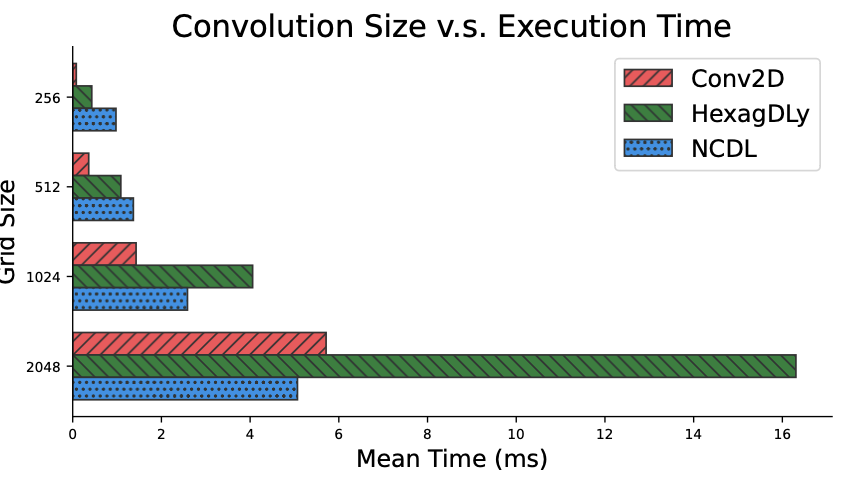
Horacsek, Joshua, and Usman Alim. "NCDL: Non-Cartesian Deep Learning ", Submitted to NeurIPS 2023.
What are the challenges?
Challenge 4: Usability
Most of the techniques used for non-Cartesian computing are not used due to the slight conceptual difficulty in understanding the geometry and theory behind non-Cartesian computing.
Background:
- Many works provide implementations for various box-spline lattice combinations [2,3,4,5,6].
- However, these works tend to be specific to the application for which they were developed and are not easily generalizable outside of those contexts.
- There is one work that attempts to provide a library for lattice queries, but this work is also quite specific and does not bother with interpolation [17].
What are the challenges?
Challenge 4: Usability
How do we support non-Cartesian methods?
NCDL
Non-Cartesian Deep Learning
- Provides a data structure for lattice data, but using tensors (in PyTorch)
- Generalizes many of the ideas in PyTorch to the non-Cartesian world
- Hopes to bring the benefit of non-Cartesian methods to deep learning
- Leverages all the theory built up until now to provide an easy to use interface for practical non-Cartesian computing
Horacsek, Joshua, and Usman Alim. "NCDL: Non-Cartesian Deep Learning ", Submitted to NeurIPS 2023.
What are the challenges?
Challenge 4: Usability
Horacsek, Joshua, and Usman Alim. "NCDL: Non-Cartesian Deep Learning ", Submitted to NeurIPS 2023.
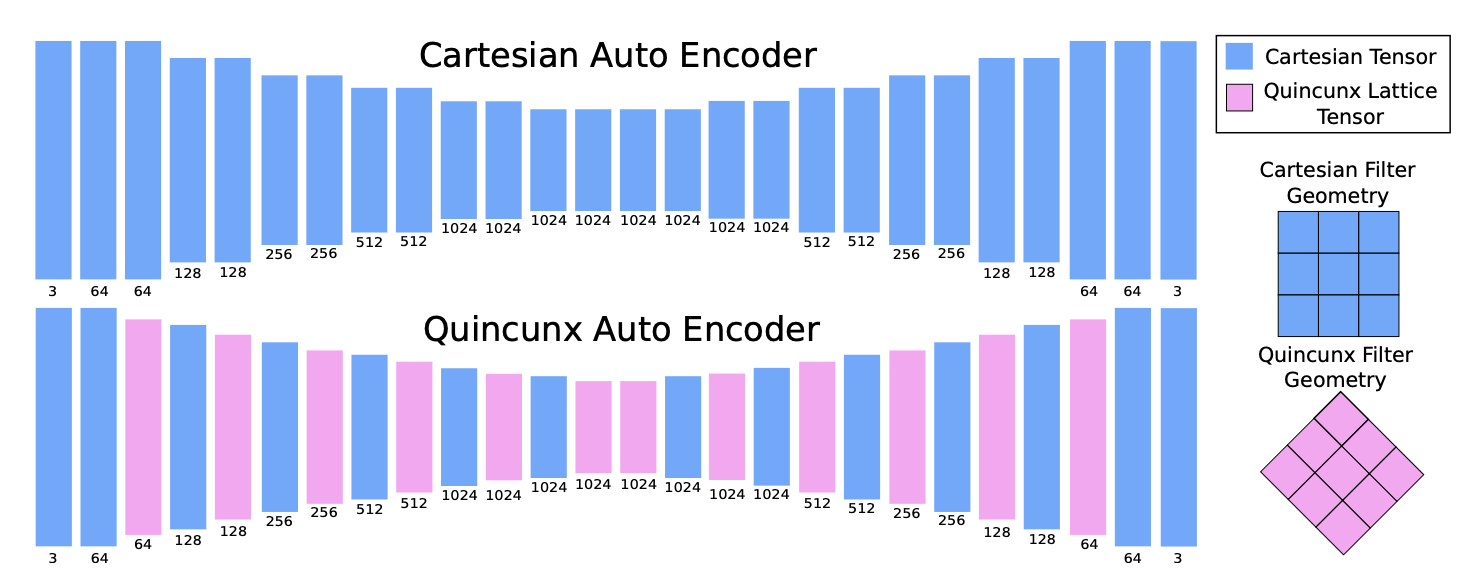
What are the challenges?
Challenge 4: Usability
Horacsek, Joshua, and Usman Alim. "NCDL: Non-Cartesian Deep Learning ", Submitted to NeurIPS 2023.
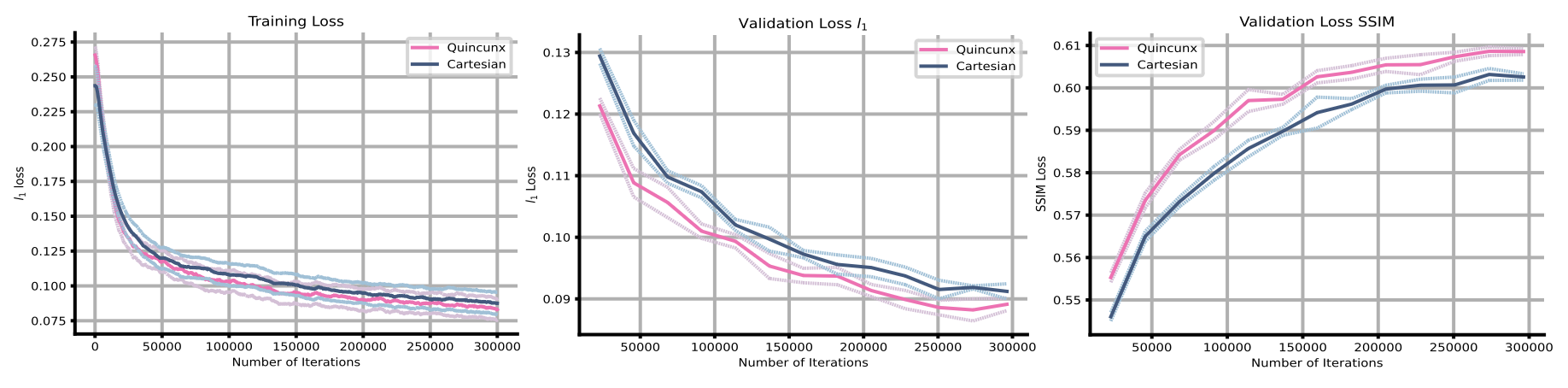
Trained on FFHQ (face dataset)
Contributions
Horacsek, Joshua, and Usman Alim. "NCDL: Non-Cartesian Deep Learning ", Submitted to NeurIPS 2023.
Horacsek, Joshua, and Usman Alim. "FastSpline: Automatic Generation of Interpolants for Lattice Samplings" ACM Transactions on Mathematical SoftwareVolume, 49 Issue 2 pp 1–35, https://doi.org/10.1145/3577194
Horacsek, Joshua, and Usman Alim. "A closed PP form of box splines via Green’s function decomposition." Journal of Approximation Theory 233 (2018): 37-57.
Tentative Timeline
- Jul 7: Committee meeting
- Aug 26th: Thesis draft
- End of Sept: Thesis Sumbission
- Late Oct early Nov: Defence
Thanks!
References
[1] Alireza Entezari. Towards computing on non-cartesian lattices. IEEE Transactions on Visualization and Computer Graphics, 2006.
[2] A. Entezari, R. Dyer, and T. Moller. Linear and cubic box splines for the body-centered cubic lattice. In IEEE Visualization 2004, pages 11–18, 10 2004.
[3] Alireza Entezari and Torsten Moller. Extensions of the Zwart-Powell box spline for volumetric data reconstruction on the cartesian lattice. IEEE Transactions on Visualization and Computer Graphics, 12(5):1337–1344, 2006.
[4] Alireza Entezari, Dimitri Van De Ville, and Torsten M ̈oeller. Practical box splines for reconstruction on the body-centered cubic lattice. IEEE Transactions on Visualization and Computer Graphics, 14(2):313–328, 2008.
[5] Minho Kim, Alireza Entezari, and Jorg Peters. Box spline reconstruction on the face-centered cubic lattice. IEEE Transactions on Visualization and Computer Graphics, 14(6), 2008.
[6] Minho Kim. Quartic box-spline reconstruction on the BCC lattice. IEEE Transactions on visualization and computer graphics, 19(2):319–330, 2013.
[7] Mahsa Mirzargar and Alireza Entezari. Voronoi splines. IEEE Transactions on Signal Processing, 58(9):4572–4582, 2010.
[8] Joshua Horacsek and Usman Alim. A closed PP form of box splines via green’s function decomposition. Journal of Approximation Theory, 233:37–57, 2018.
[9] Thierry Blu and Michael Unser. Quantitative Fourier analysis of approximation techniques. I. interpolators and projectors. IEEE Transactions on signal processing, 47(10):2783–2795, 1999.
[10] Balazs Csebfalvi and Gergely Racz. Retailoring box splines to lattices for highly isotropic volume representations. In Computer Graphics Forum, volume 35, pages 411–420. Wiley Online Library, 2016.
[11] Zhou Wang, Alan C Bovik, Hamid R Sheikh, and Eero P Simoncelli. Image quality assessment: from error visibility to structural similarity. IEEE transactions on image processing, 13(4):600–612, 2004.
[12] Thomas Fogal, Alexander Schiewe, and Jens Kruger. An analysis of scalable GPU-based ray-guided volume rendering. In 2013 IEEE Symposium on Large-Scale Data Analysis and Visualization (LDAV), pages 43–51. IEEE, 2013.
[13] Jesus Dıaz-Garcıa, Pere Brunet, Isabel Navazo, and Pere-Pau Vazquez. Progressive ray casting for volumetric models on mobile devices. Computers & Graphics,73:1–16, 2018.
[14] Jiro Inoue and A James Stewart. Multiresolution sphere packing tree: a hierarchical multiresolution 3d data structure. In Proceedings of the 2008 ACM symposium on Solid and physical modeling, pages 367–373, 2008.
[15] JJ Horacsek and UR Alim. Compactly supported biorthogonal wavelet bases on the body-centered cubic lattice. In Computer Graphics Forum, volume 36, pages35–45. Wiley Online Library, 2017.
PCC
By Joshua Horacsek
