CurviSlicer: Slightly curved slicing for 3-axis printers
Jimmy Etienne, et al.

Introduction
Since we don't do a lot of digital fab...
Additive
Subtractive
- Fused Deposition Modelling (FDM)
- Stereolithography (SLA)
- Selective Laser Sintering (SLS)
- Etc...
- CNC Milling
- CNC Lathe
- Foam Cutting
- etc...
Computer Numerically Controlled = CNC
FDM Printing
Generally a simple concept, FDM deposits material via CNC machineary
FDM Printing
Generally a simple concept, FDM deposits material via CNC machineary

3D Printing
Anatomy

3D Printing
Hotend

3D Printing
Slicing

Slightly Curved Slicing
Addresses a weakness of FDM printers

Slightly Curved Slicing

Addresses a weakness of FDM printers
Slightly Curved Slicing
High level approach
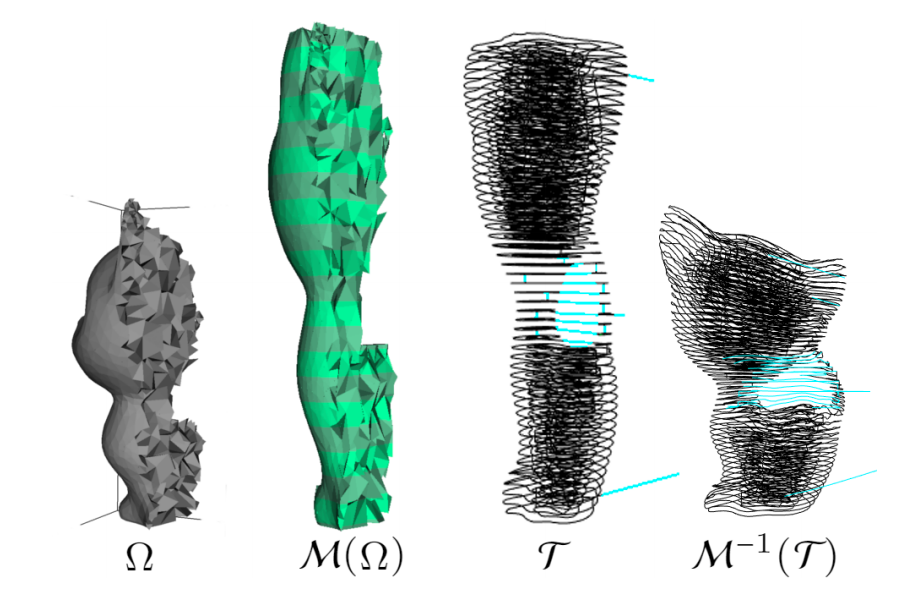
Tetrahedralize
Optimization
Toolpath Generation
Post Processing
Slightly Curved Slicing
Tetrahedralization
Provides a means of representing \(\mathcal{M}\)
\(\Omega\) - Mesh
\(\Gamma\) - Tetrahedral mesh (\(\Gamma_I\) inside \(\Gamma_O\) and out)
\(\mathcal{F}\) - Faces on mesh
\(\forall p \in V, \mathcal{M}(p) = h\) (height)
Fabrication Constraints
Layer thickness
Minimum and maximum layer thicknesses

\(\tau_{min} = 0.1d\), \(\tau_{max} =0.75d\)
For 0.4mm nozzle, this gives [0.04mm, 0.3mm], depending on calibration
Fabrication Constraints
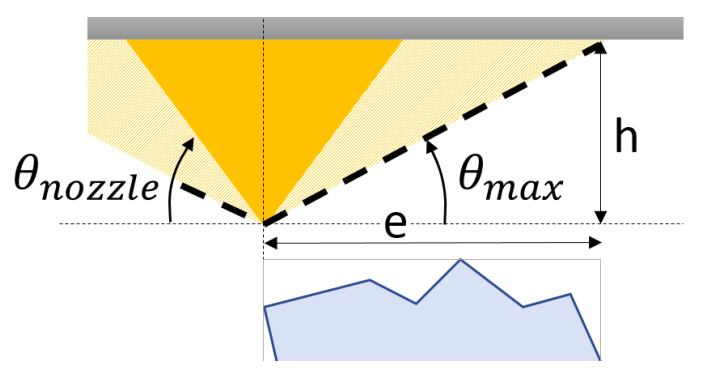
Slope
Key Intuition
Slice at \(\tau_{max}\) in \(\mathcal{M}(\Omega)\), optimize \(\mathcal{M}\) to flatten as many faces as possible
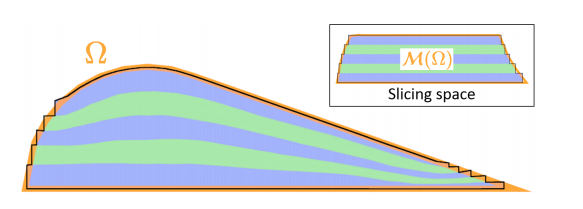
Flatten which faces?
\(\overline{\mathcal{F}}\) - other faces
\(\underline{\mathcal{F}}\) - faces to be flattened
Objective Function
Define an energy function to minimize
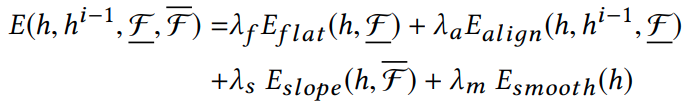
\(\lambda\)s are user-chosen trade-off parameters
\(h^0=z\)
Objective Function
Define an energy function to minimize
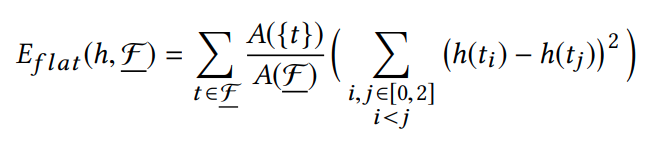
Attempts to pull vertices of a triangle to the same height
Objective Function
Define an energy function to minimize
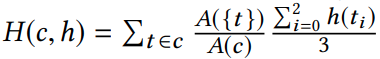
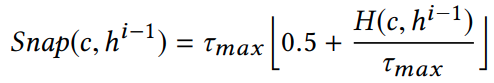
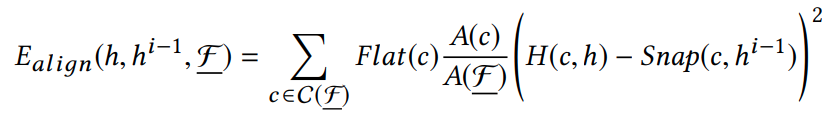
\(\mathcal{C}(\underline{\mathcal{F}})\) is the set of connected components of the set to flatten
Objective Function
Define an energy function to minimize
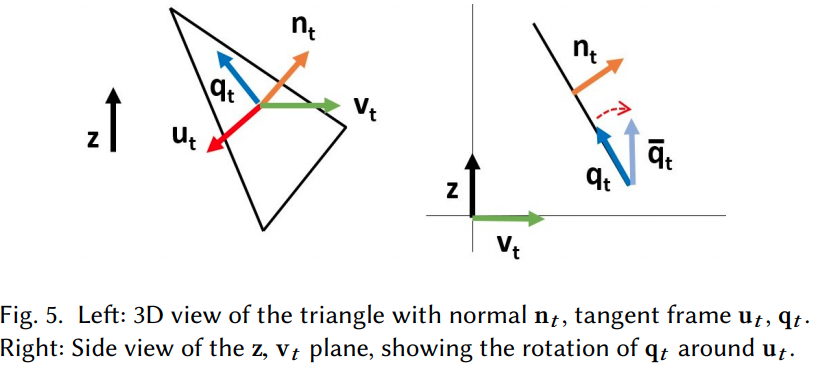
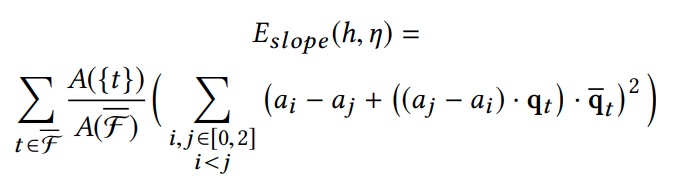
Objective Function
Define an energy function to minimize
Attempts to pull vertices of a triangle to the same height
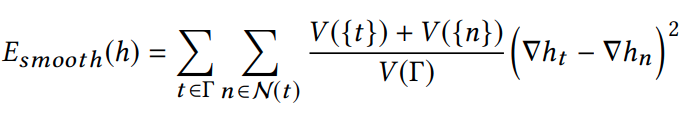
Objective Function
Constraints on optimization
Thickness constraint
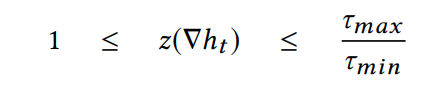
\(\forall t\in \Gamma_I\)
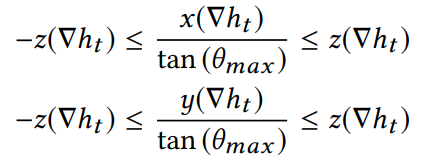
Slope constraint
\(\forall t\in \Gamma_I\)
Objective Function
What if flattened surfaces aren't flat?
Objective Function
What if flattened surfaces aren't flat?

Printing
Extrusion rate must be modified in \(\mathcal{T}\), but is available from the gradient of \(\mathcal{M}\)

Results

Results

Results

Results
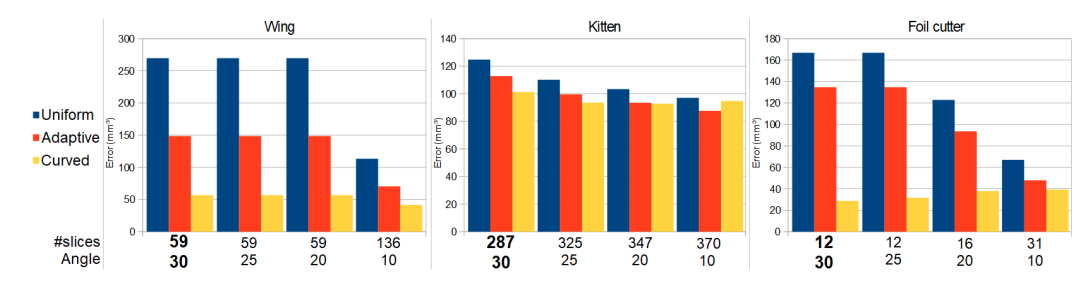
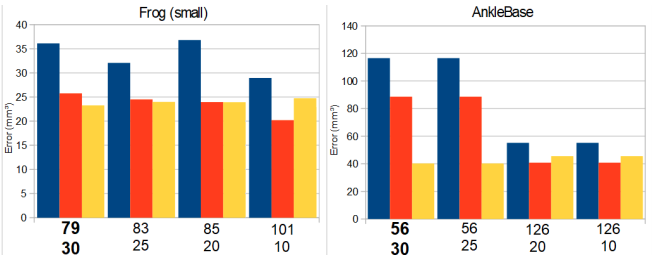
Error Comparison
CurviSlice
By Joshua Horacsek
CurviSlice
- 1,256



