Depth-Aware Video Frame Interpolation
PhD Candidate
Fall 2020
Wenbo Bao et al.
Context
Temporal up-sampling of video data
Approach?
Machine learning, obviously, but what's the intuition?
- Depth aware optical flow calculation
- Encorporate warping into architecture
- Composition of architectures that are pre-trained to solve problems
This work is a good example of using domain knowledge and transfer learning to produce a state of the art model.
Optical Flow
Models motion between two frames of video
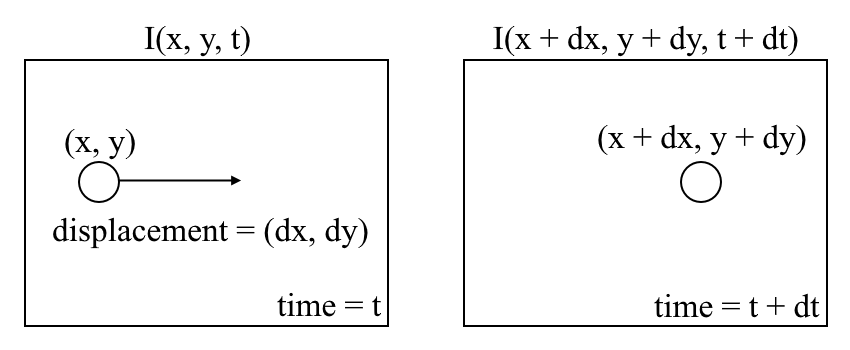
Optical Flow
Visualization


- Hue encodes direction
- Saturation encodes magnitude of displacement
Schuster, R. et al. Combining Stereo Disparity and Optical Flow for Basic Scene Flow
Warping
Warping the image at time \(t\) by the opical flow produces an image similar (no brightness change) to the image at time \(t+1\).



Network
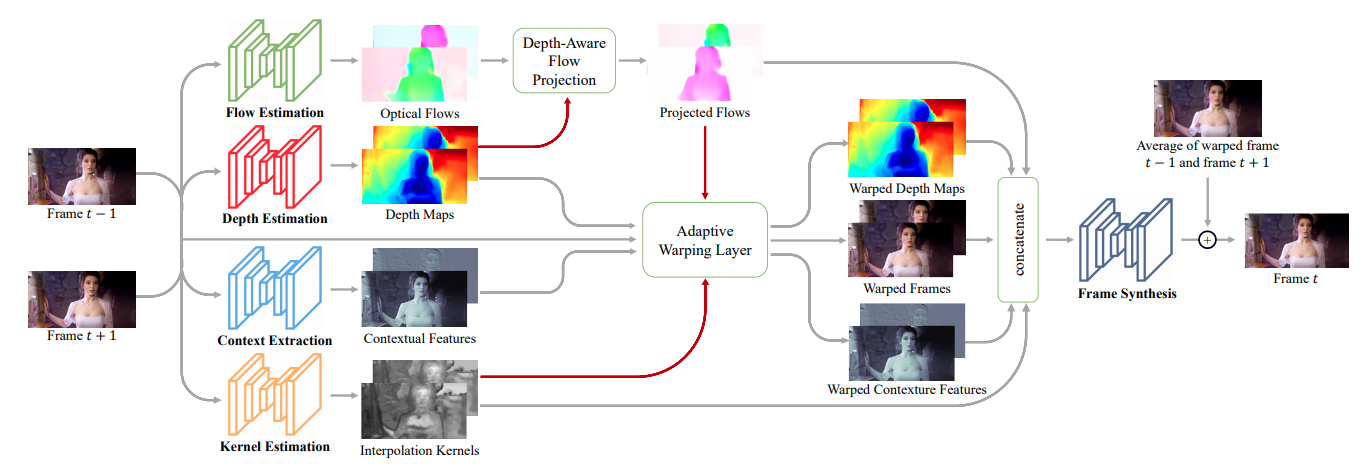
Transfer learning!
Network
Flow Estimation
Depth estimation
D. Sun. PWC-net: CNNs for optical flow using pyramid, warping, and cost volume.
- Uses pretrained PWC weights
- Flow calculation is not a well posed problem, additional constraints must be added (good application for ML)
L. Zhengqi. MegaDepth: Learning Single-View Depth Prediction from Internet Photos
- Uses pretrained network weights
Provides depth maps \(D_0(\mathbf{x})\)and \(D_1(\mathbf{x})\) for the two input frames.
Provides flow functions \(\mathbf{F}_{0\to 1}(\mathbf{x})\) and \(\mathbf{F}_{1\to 0}(\mathbf{x})\) for the two input frames.
Network

Incorporate depth information
Depth Aware Flow Projection
Depth is an important cue, closer objects are more important, helps define object boundaries
\(\mathbf{F}_{t\to 0}(\mathbf{x})=-t\cdot \frac{\displaystyle\sum_{\mathbf{y}\in\mathcal{S}(\mathbf{x})}w(\mathbf{y})\cdot\mathbf{F}_{0\to 1}(\mathbf{y})}{\displaystyle\sum_{\mathbf{y}\in\mathcal{S(\mathbf{x})}}w(\mathbf{y})}\), with \(w_0(\mathbf{y})=\frac{1}{D_0(\mathbf{y})}\)
(similarly for \(\mathbf{F}_{t\to 1}(\mathbf{x})\) )
\(S(\mathbf{x})=\{y:round(\mathbf{y} + t\cdot\mathbf{F}_{0\to 1}(\mathbf{y})) = \mathbf{x}, \ \forall \mathbf{y} \}\)
Network

Encorporate depth information
Adaptive Warping Layer
Actively warps input
\(\mathbf{\hat{I}}(\mathbf{x})=\displaystyle\sum_{r\in[-R+1, R]^2}k_\mathbf{r}(\mathbf{x})\mathbf{I}(\mathbf{x} + \lfloor \mathbf{F}(\mathbf{x})\rfloor + \mathbf{r})\)
Learned Kernel (makes this 'adaptive')
W. Bao et al. MEMC-Net: Motion Estimation and Motion Compensation Driven Neural Network for Video Interpolation and Enhancement
Note these transformations have been differentiable!
Network

U-Net architecture, not pre-trained, then reshaped for the adaptive warping layer.
O. Ronneberger et al. U-Net: Convolutional Networks for Biomedical Image Segmentation
Network

Context extraction isn't that interesting, a bunch of residual blocks (not pretrained, 7x7 convolution blocks ReLU and skips...)
Network

Frame synthesis, stacked residual blocks
Training

Params: AdaMax with \(\beta_1=0.9, \beta_2=0.999\), batch size of 2, learning rate = 1e-4, 1e-6, 1e-7
Pretrained
Training: 30 epochs, half the learning rate then 10
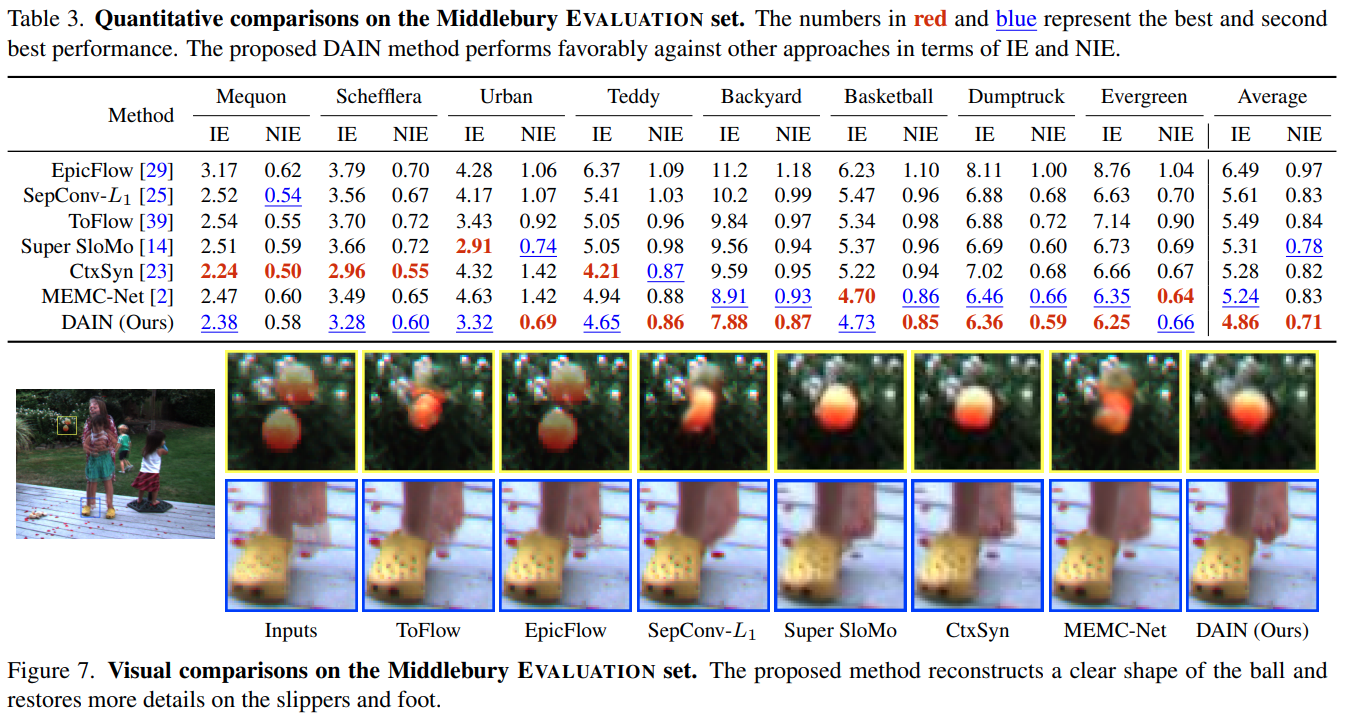
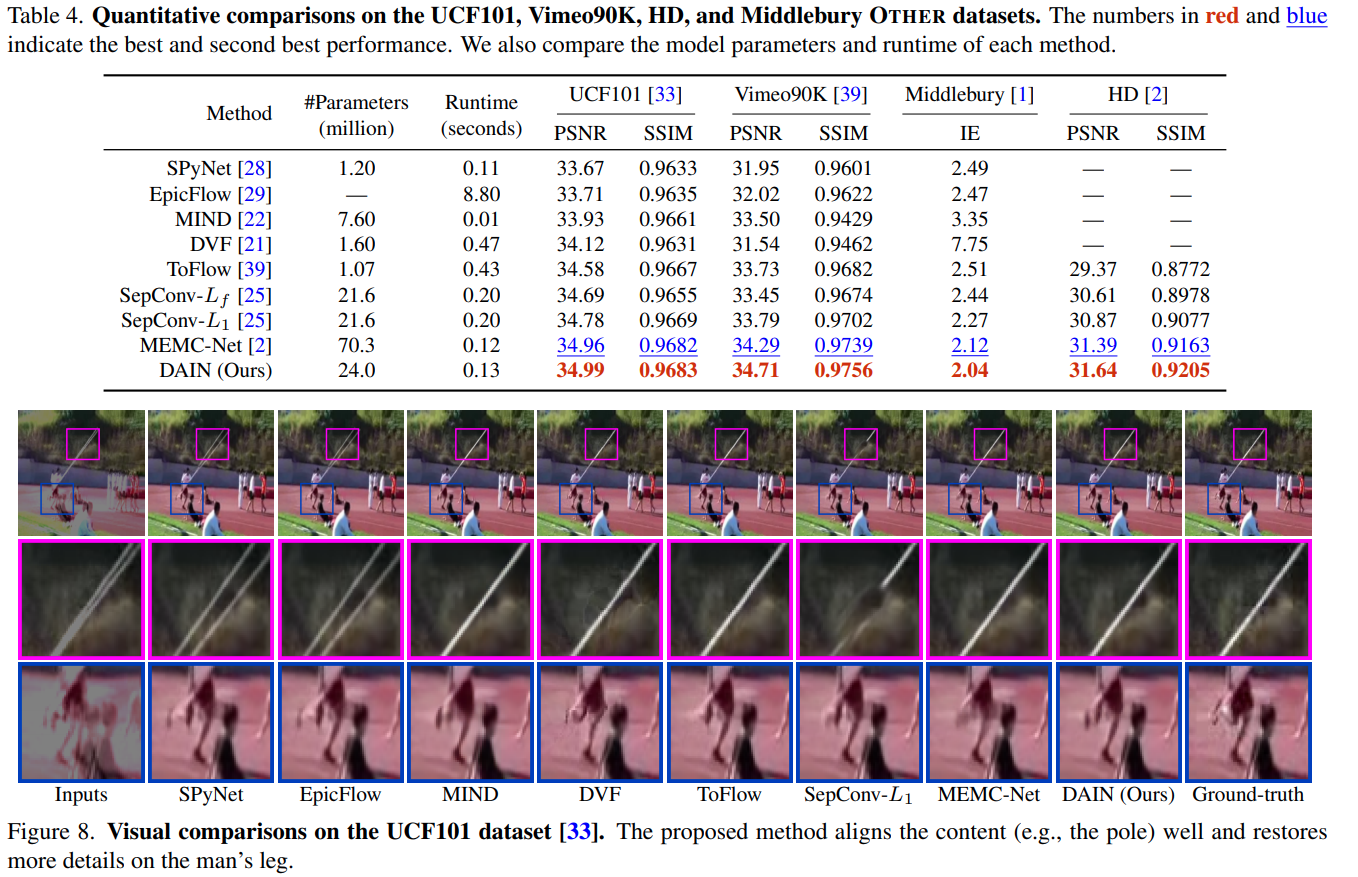
Experiments
- Ran on a variety of datasets: Milddlebury, Vimeo90K, UCF101, HD (see paper for references)
- Different metrics: Interpolation Error (IE) PSNR and SSIM (depending on the dataset)
- Assess the components of the network
- Assess the performance of the network
Experiments
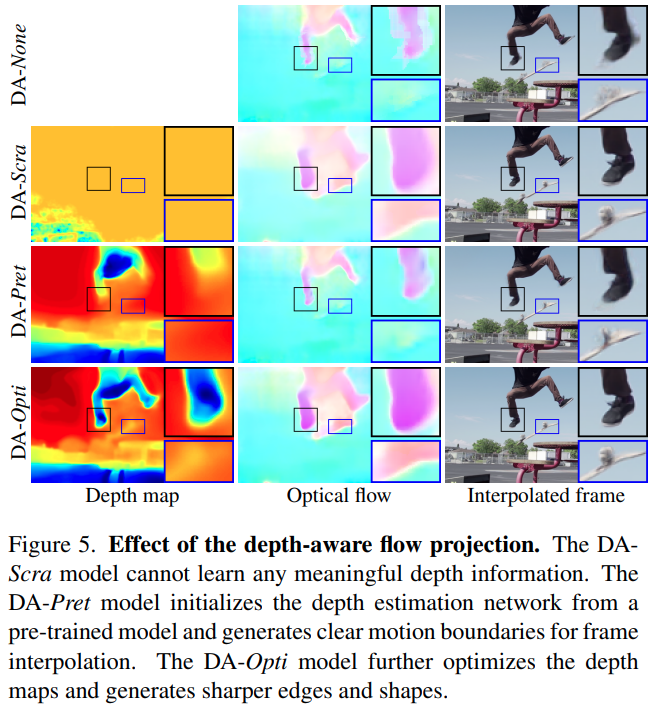
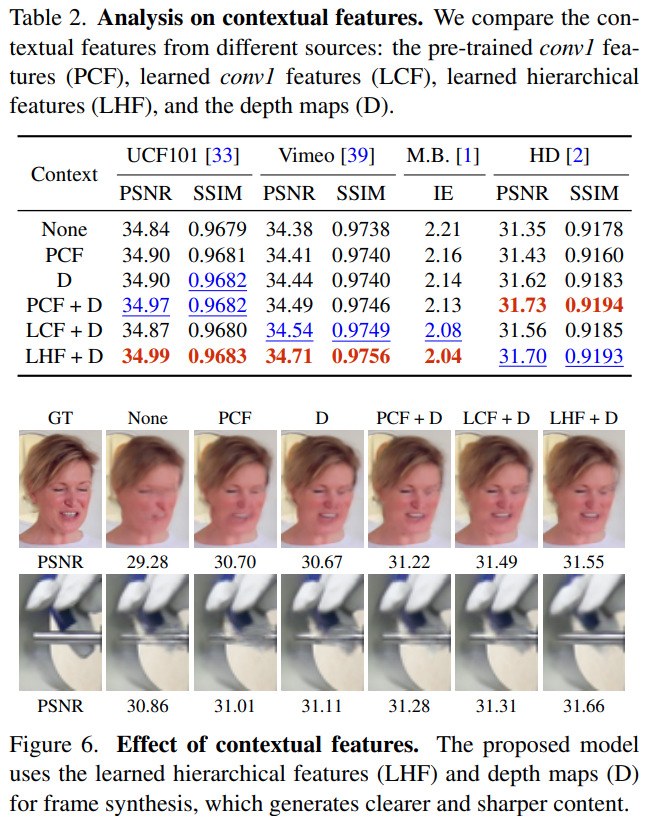
Results
Results
Dain
By Joshua Horacsek
Dain
- 1,005



