Deep Learning
A Primer
Feb 8th 2018
J. Horacsek
What is Deep Learning?
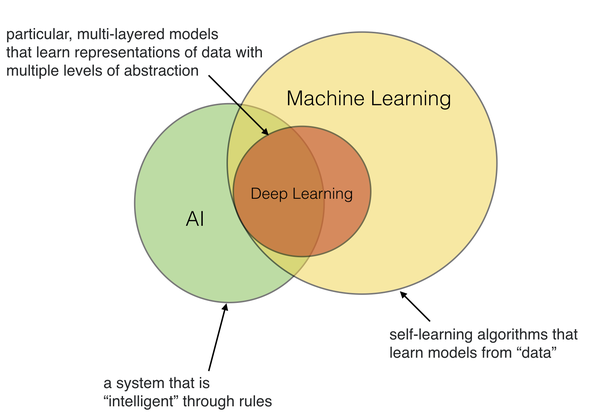
What is Deep Learning?
Practically, deep learning can be thought of as very deep neural networks
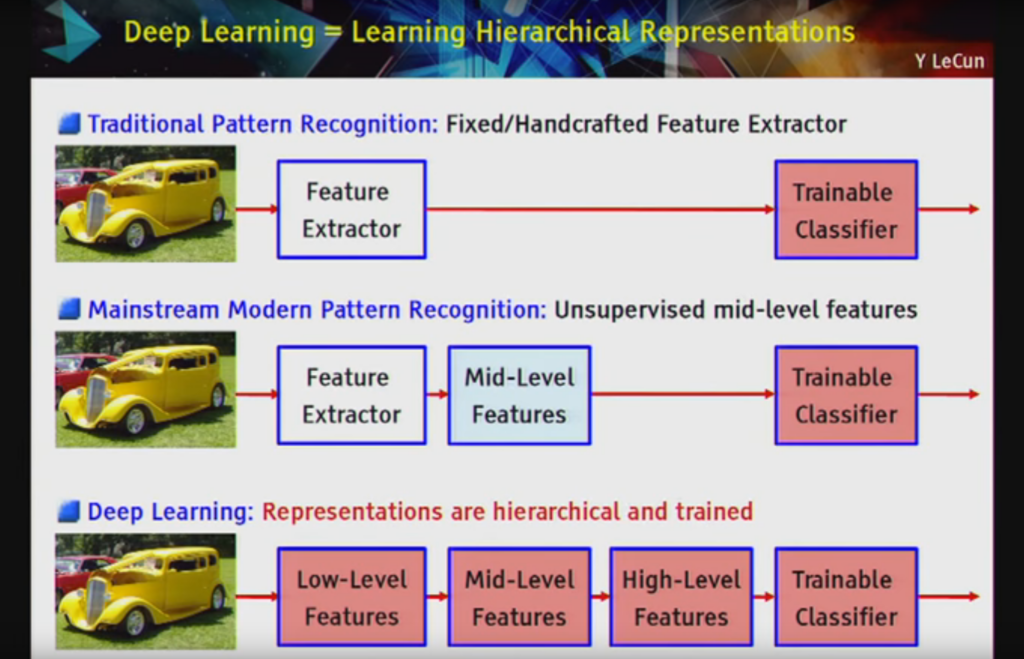
Why is it important?
Real world problems are often not well posed.
Take an image as input, does that image contain a dog?
Why is it important?

Why is it important?

Why is it important?

Why is it important?
Real world problems are often not well posed.
We'll stick to supervised learning and classifiers here.
Take an image as input, does that image contain a dog?
We have the data + labels
The data fall into classes (cats vs. dogs)
What is Deep Learning?
Practically, deep learning can be thought of as very deep neural networks

Why is it important?
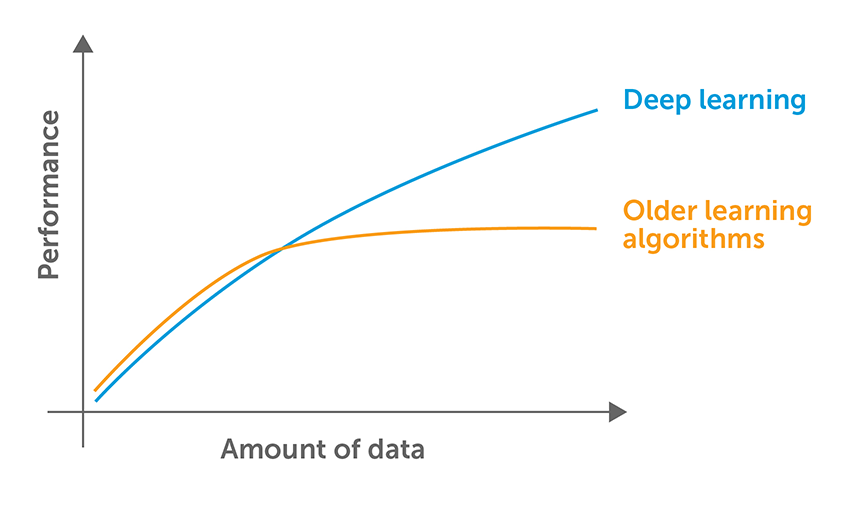
Why is it important?
Recipe for a good deep learning algorithm
- A good architecture
- LOTS of data
- LOTS of training
This isn't an exhaustive list (other research in deep learning has also contributed, dropout, activation functions, optimization, etc..)
What is Deep Learning?
Practically, deep learning can be thought of as very deep neural networks
What is Deep Learning?
What is Deep Learning?
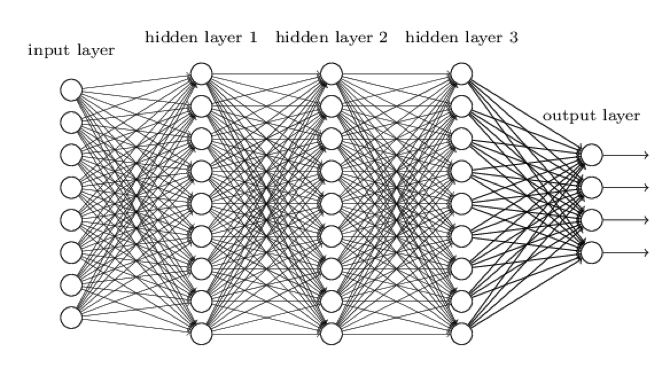
\(N(\vec{x})\) is the "function" that represents the neural net -- \(\vec{x}\) can be an image, audio signal or text
What is Deep Learning?
What is Deep Learning?
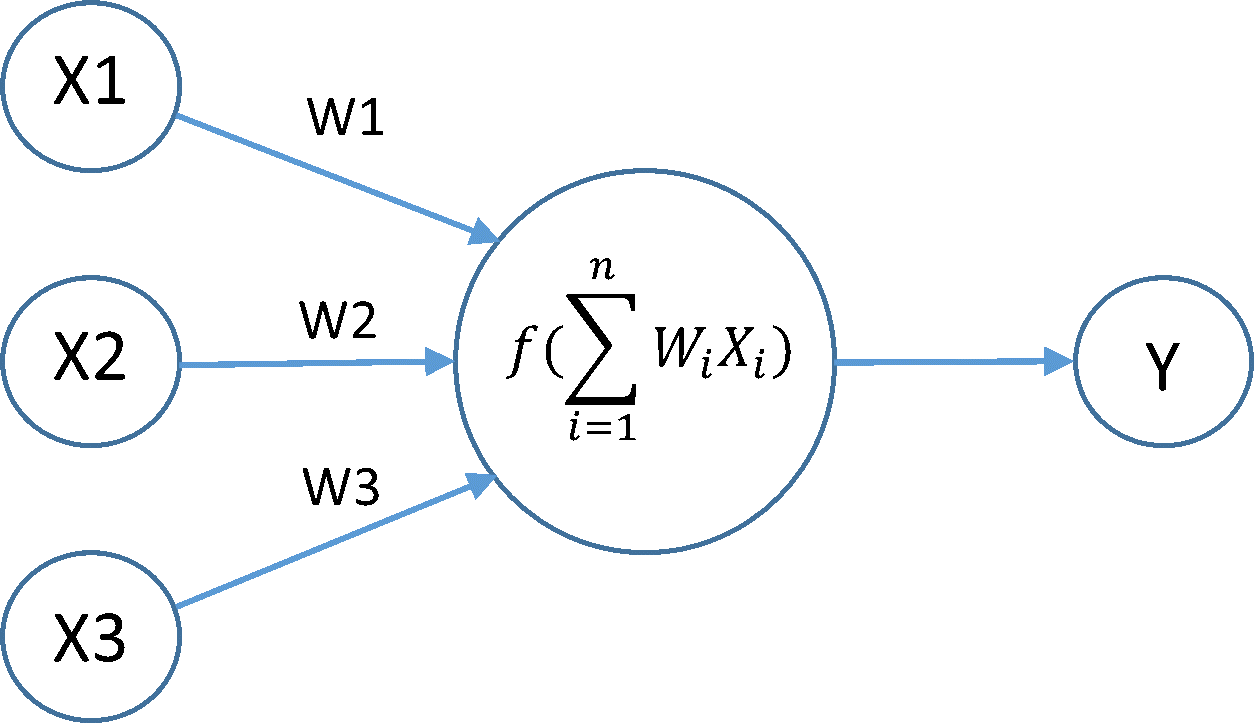
\(f(x)\) is an activation function
What is Deep Learning?
\(f(z)\)
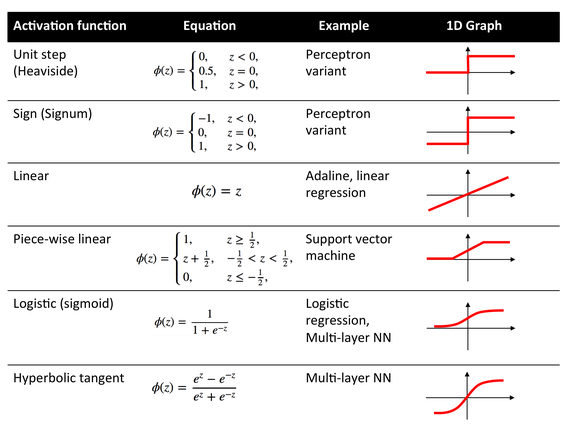
\(f(z)\)
\(f(z)\)
\(f(z)\)
\(f(z)\)
\(f(z)\)
ReLU: \(f(z) = H(z)z\) where \(H(z)\) is the heaviside function.
How to train networks?
Training takes a lot of data
Many \((\vec{x}_i, {y}_i)\) pairs, where \(\vec{x}_i\) is say, an image and \(y_i\) encodes the output (say, 0 for no dog, 1 for dog).
\(J(W) = \sum_i E(x_i, y_i, W)\)
Minimize error function
\(E(x,y,W) = (N(x,W)-y)^2\)
Here, \(E(x,y)\) is an error function, we could use
But there are many different error metrics
How to train networks?
Minimize via stochastic gradient descent start with \(W_0\) as a random vector
\(W_{i+1} = W_{i} - \gamma \nabla_W J(W_i) \)
Minimize error function via
Need to be able to compute \(\nabla_W N(x) \), which we can do via back propogation (i.e. the chain rule).
I'm not going to go over this here, this important, but it's more important to know that backprop=derivative.
History
Neural nets have existed since the 1980's, (perhaps even earlier) why are they so successful right now?
Training is computationally expensive, highly parallel computers and GPUs meet this need
However, architectural advancement have also been extremely important
Dense Networks

Are all these connections necessary/useful?
Dense Networks
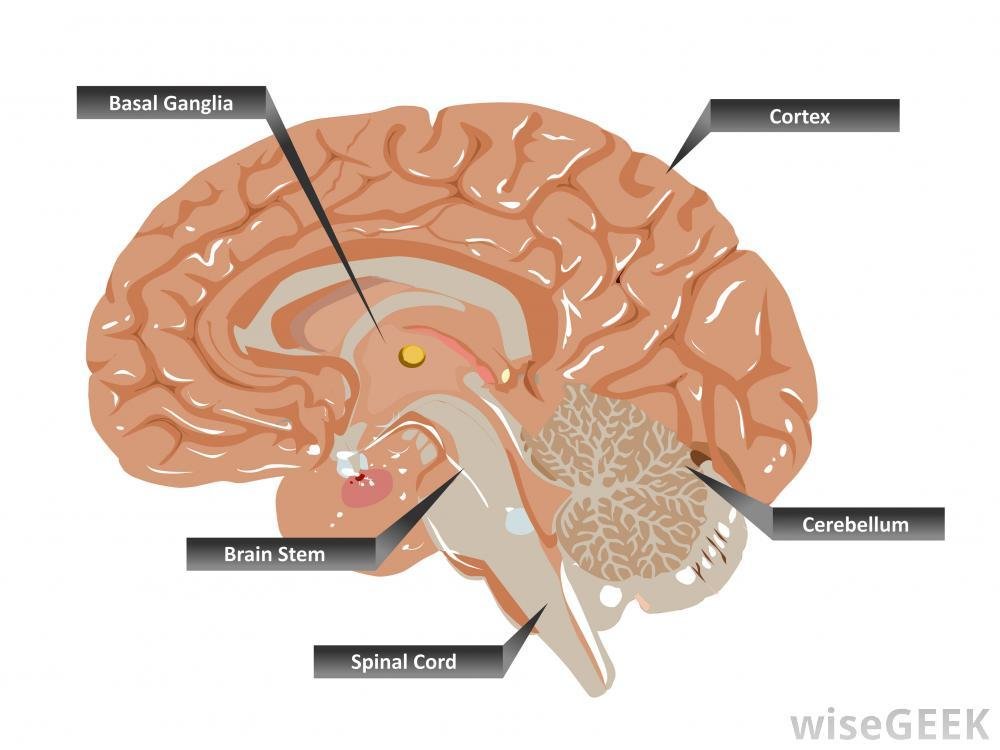
The brain has a multitude of different cell structures
Dense Networks

The brain has a multitude of different functional "compartments"
Dense Networks
It's incredibly naive to think that dense networks would generalize well
Convolutional Networks
Instead, take another cue from biology, as well as trying to incorporate spatial locality
Small receptive fields, hierarchical representation
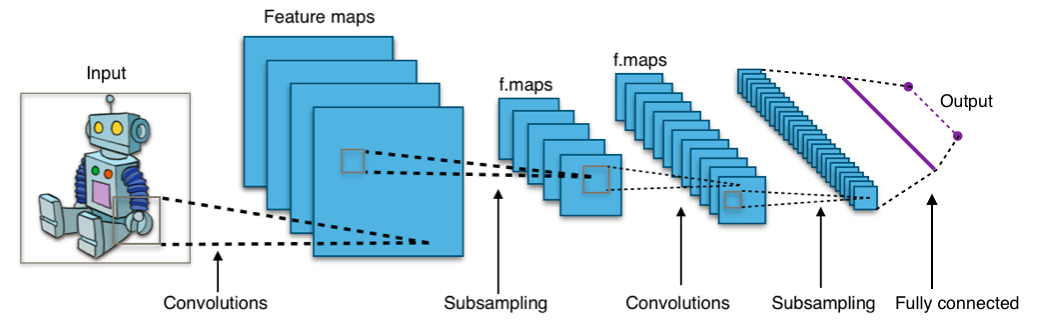
Convolutional Networks
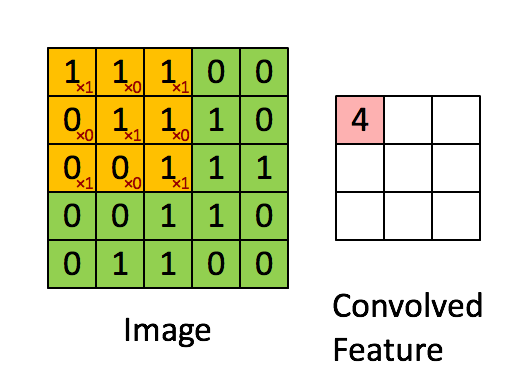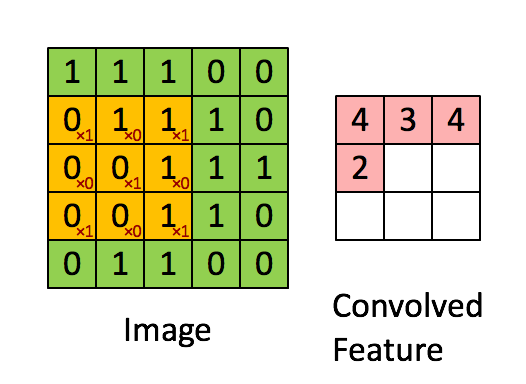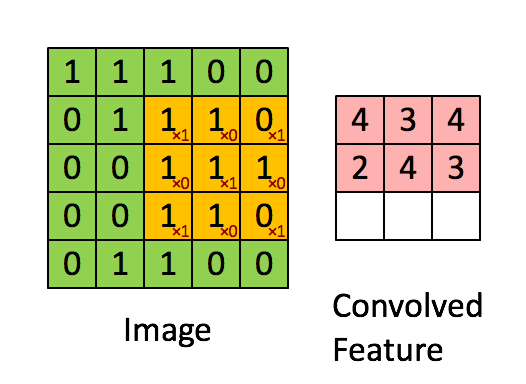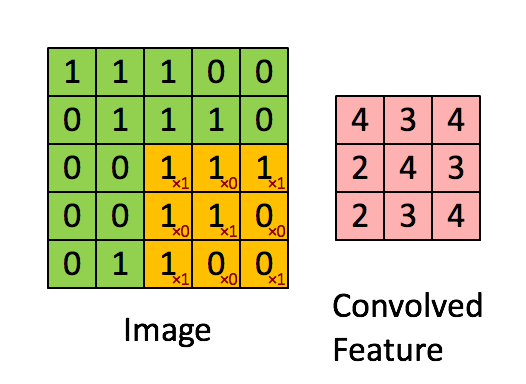
Define a mask that is shifted over each pixel of the image
Weights are unknown, found using SGD.
Convolutional Nodes
Convolutional Networks
Convolutional Nodes
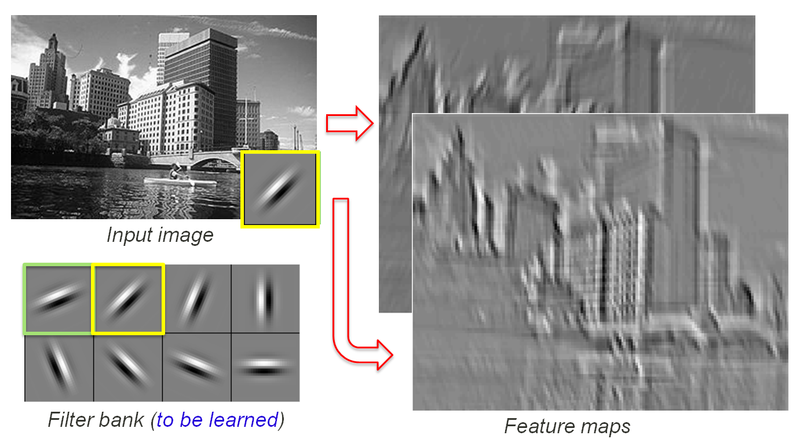
Convolutional Networks
Convolved feature is then passed through a non linearity (activation function, usually ReLU)
But this is still a large image, we want to look at it at multiple scales
Convolutional Networks
Max Pooling Layers
Increadibly simple idea, look at the nodes that are have highest activation in an area
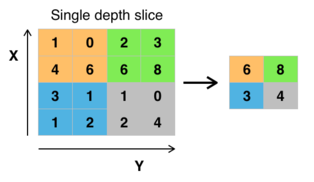
Produces a lower resolution map of important features
Convolutional Networks
These additions are really what reinvigorated research in neural nets
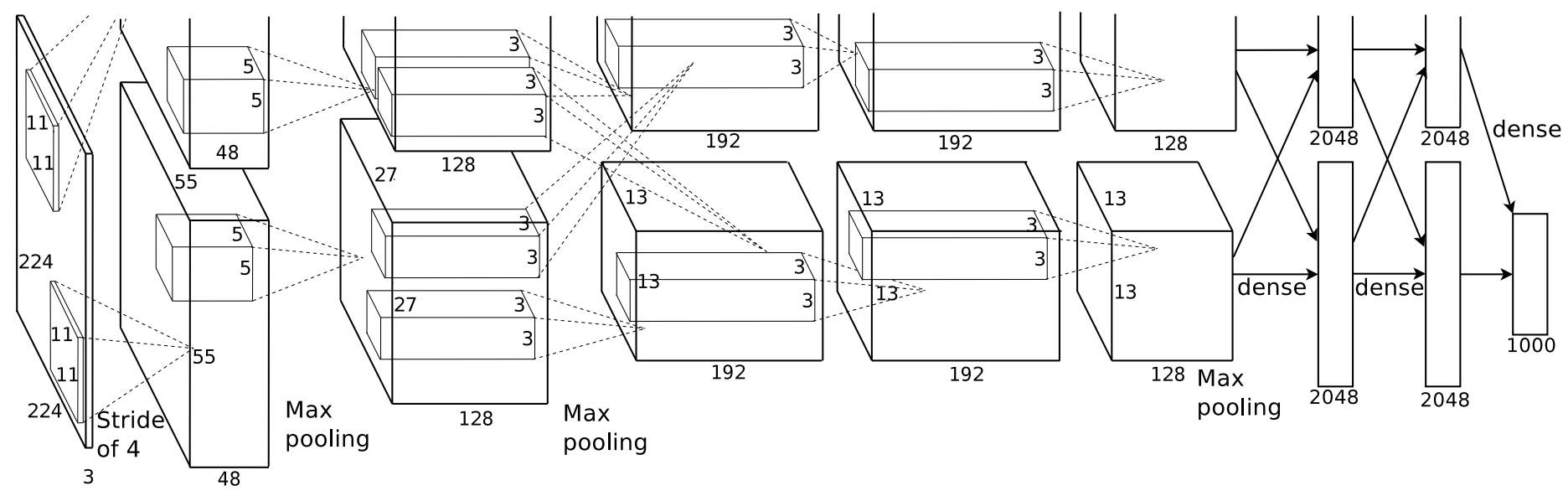
Additional resources...
Of course not, libraries like Tensor Flow and Theano do all the hard math.
Do you need to code all this from scratch?
Online resources:
Deep Learning
By Joshua Horacsek
Deep Learning
- 1,345



