Fast Spline Evaluation
(finally)
J. Horacsek
April 17th 2020
Preface
This still isn't finished :)
There've been a lot of setbacks, whenever I've been close, problems arose
Where we're going
- Box splines (Voronoi splines too)
- Approximation spaces
- Optimization (a lot of little optimizations)
- Low level code generation (LLVM)
- CPU and GPU codegen (the absolute PAIN of trying to compile and statically link PTX)
Motivation
For scalar vis, we often care about evaluating functions of the form
f(x) = \displaystyle\sum_{n\in L\mathbb{Z}^3}c_n \ \varphi(x-n)
And we want to do this quickly on the GPU; this is required for interactive visualization of datasets
Going fast on the GPU
Application dictates speed, but we can make some observations to speed up computations
- No branches in code (or at least reduce branches)
- Minimize expensive memory fetches (by organizing fetches and using trilinear fetches)
- Waste computation if necessary (the process is already bandwidth limited, it's ok to waste computation)
Motivation
Approximation in 1D
Motivation
Approximation in 1D
Motivation
Approximation in 1D
f_1
f_2
f_3
f_4
f_5
f_6
f_7
Motivation
Approximation in 1D
f_1
f_2
f_3
f_4
f_5
f_6
f_7
Motivation
Approximation in 1D
f_7
f_1
f_2
f_3
f_4
f_5
f_6
\tilde{f}(x) = \displaystyle\sum^7_{n=1}f_n\beta_1(x-n)
Motivation
Approximation in 1D
f_7
f_1
f_2
f_3
f_4
f_5
f_6
\tilde{f}(x) = \displaystyle\sum^7_{n=1}f_n\beta_1(x-n)
\(\tilde{f}(x) = f_{\lfloor x \rfloor}(1-(x-\lfloor x \rfloor)) + f_{\lfloor x \rfloor + 1}(x-\lfloor x \rfloor) \)
Sampling Lattices
Cartesian Lattice
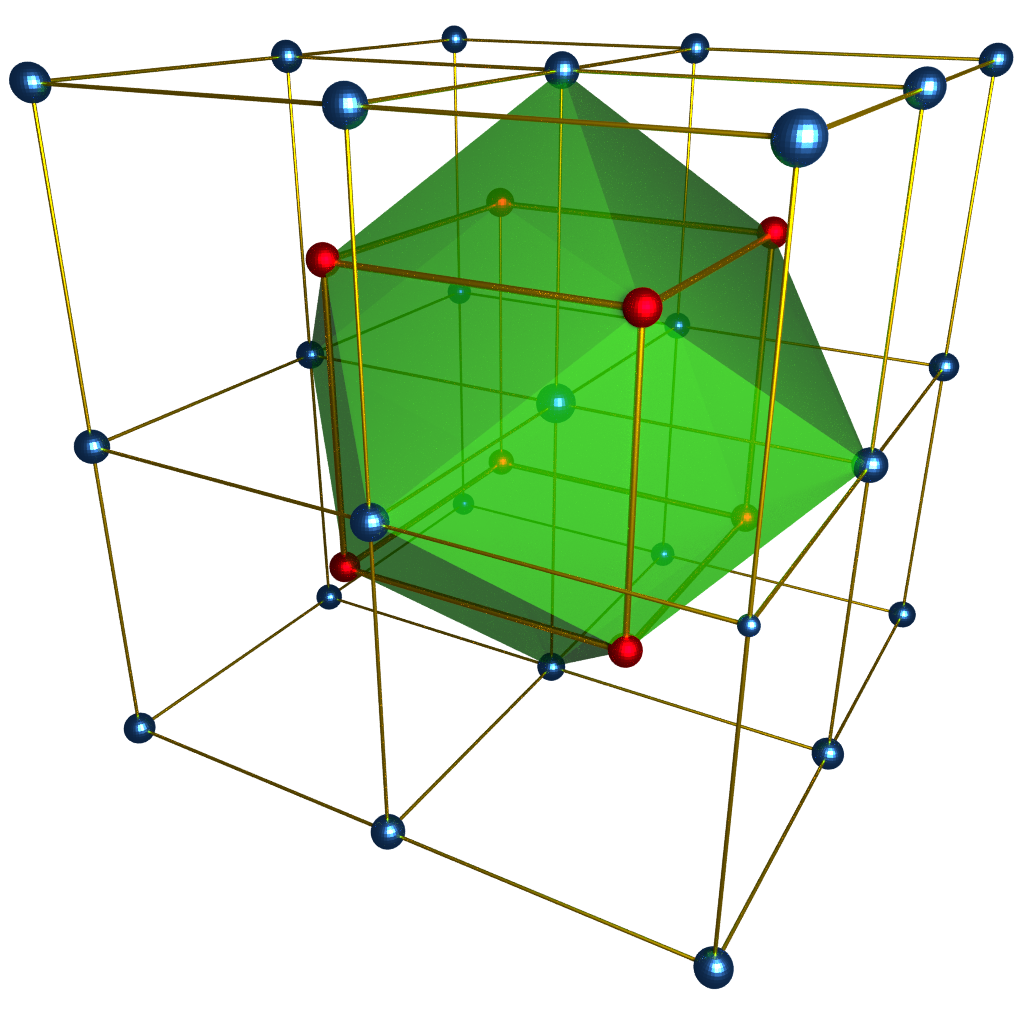
Body Centered Cubic Lattice
\displaystyle\sum_{n\in L\mathbb{Z}^3}c_n \ \varphi(x-n)
L controls the point distribution
Box Splines
Multivariate extension to B-splines
- Compact
- Smooth
- Piecewise polynomials
\Xi = \begin{bmatrix}
| & | & \ & | \\
\xi_1 & \xi_2 & ... & \xi_n \\
| & | & \ & |
\end{bmatrix}
Start with a direction matrix
\xi_i \in \mathbb{R}^s
Box Splines
Convolutional, recursive definition
M_\Xi(x) = \displaystyle\int_0^1M_{\Xi\backslash\xi}(x - t\xi) dt \text{ \ with \ } M_{[ \ ]}(x) := \delta(x)
In one dimension, this looks like
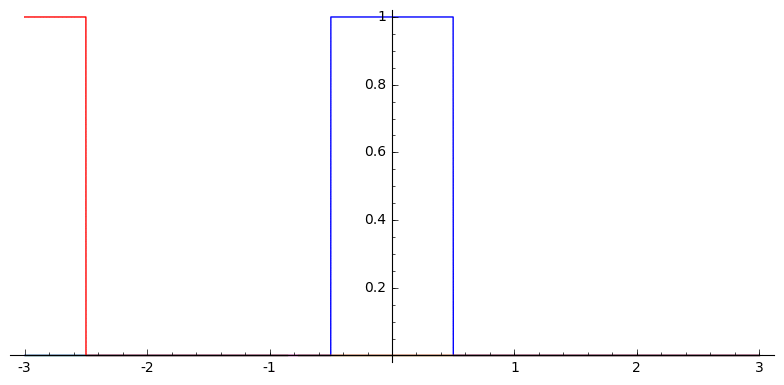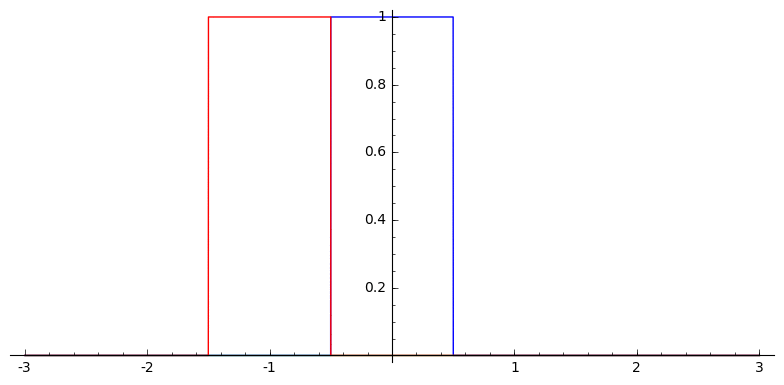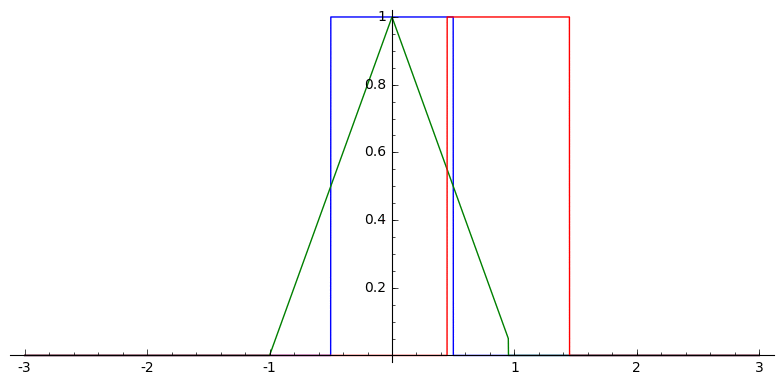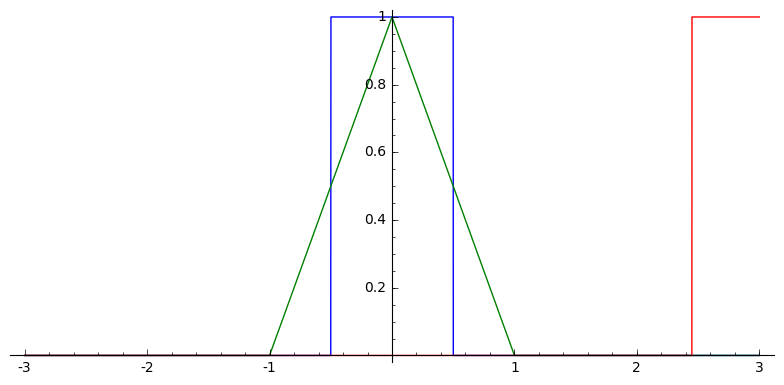
Box Splines
\Xi = \begin{bmatrix}
1 & 0 & 1 \\
0& 1 & 1
\end{bmatrix}
Box Splines
\Xi = \begin{bmatrix}
1 & 0 & 1 & -1 \\
0& 1 & 1 & 1
\end{bmatrix}
Box Splines
Multivariate extension to B-splines
- Compact
- Smooth
- Piecewise polynomials
Box Splines
We have an explicit form of evaluation
M_\Xi(x) = \displaystyle\sum_{(\gamma,p)\in S_\Xi} \sum_{(\lambda, \alpha) \in P_{n-s}} \gamma\lambda |\det\Xi_\alpha|{{[\![ (\Xi_\alpha^{-1}x) - p ]\!]}_{+}}^{\mu_\alpha - 1}.
(this is just a piecewise polynomial....)
In fact, another class of splines can be expressed as a sum of box splines
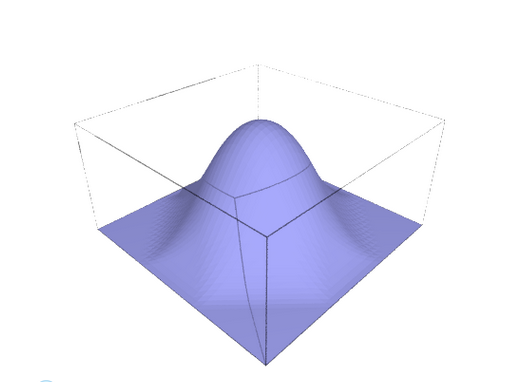
Voronoi Splines
Voronoi Splines
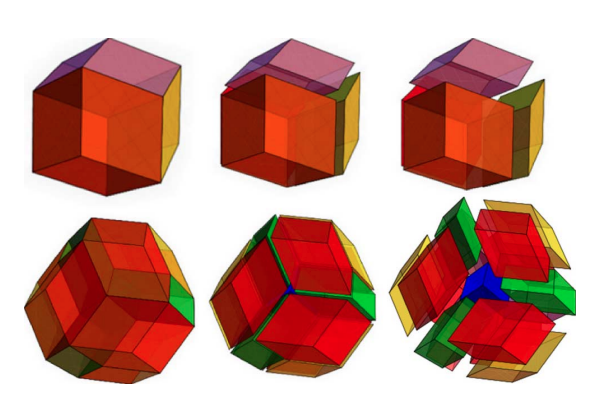
Box Splines
We have an explicit form of evaluation
M_\Xi(x) = \displaystyle\sum_{(\gamma,p)\in S_\Xi} \sum_{(\lambda, \alpha) \in P_{n-s}} \gamma\lambda |\det\Xi_\alpha|{{[\![ (\Xi_\alpha^{-1}x) - p ]\!]}_{+}}^{\mu_\alpha - 1}.
(this is just a piecewise polynomial....)
But we still have the problem of evaluating
f(x) = \displaystyle\sum_{n\in L\mathbb{Z}^3}c_n \ \varphi(x-n) = \displaystyle\sum_{n\in L\mathbb{Z}^3}c_n \ M_\Xi(x-n)
Generic Evaluation
f(x) = \displaystyle\sum_{n\in L\mathbb{Z}^3}c_n \ \varphi(x-n)
How do we write generic code for:
f(x) = \displaystyle\sum_{n\in\overline{supp(\varphi(\cdot - x))} \cap \mathbb{Z}^3 }c_n \ \varphi(x-n) \chi_{L\mathbb{Z}^3}(n)
Two C++ classes:
Lattice
Basis Function
class Lattice {
Lattice(int rx, int ry, int rz);
is_lattice_site(int rx, int ry, int rz);
get_nearest_site(float x, float y, float z);
// Get and set values
operator(int rx, int ry, int rz);
// Additional support methods
// and iterators
};class BasisFunction {
// no constructor,
// integer support from the origin
get_support_size();
//
phi(float rx, float ry, float rz);
// Additional support methods for derivatives
};\chi_{L\mathbb{Z}^3}(x) = \begin{cases}
1 & \text{ if } x \in L\mathbb{Z}^s\\
0 & \text{ otherwise }
\end{cases}
Generic Evaluation
How do we write generic code for:
f(x) = \displaystyle\sum_{n\in\overline{supp(\varphi(\cdot - x))} \cap \mathbb{Z}^3 }c_n \ \varphi(x-n) \chi_{L\mathbb{Z}^3}(n)
Lattice
Basis Function
class Lattice {
Lattice(int rx, int ry, int rz);
is_lattice_site(int rx, int ry, int rz);
get_nearest_site(float x, float y, float z);
// Get and set values
operator(int rx, int ry, int rz);
// Additional support methods
// and iterators
};class BasisFunction {
// no constructor,
// integer support from the origin
static get_support_size();
//
static phi(float rx, float ry, float rz);
// Additional support methods for derivatives
};As long as we can compute values of \(\varphi\), and we know the support of \(\varphi\), we can evaluate the convolution sum
Generic Evaluation
How do we write generic code for:
f(x) = \displaystyle\sum_{n\in\overline{supp(\varphi(\cdot - x))} \cap \mathbb{Z}^3 }c_n \ \varphi(x-n) \chi_{L\mathbb{Z}^3}(n)
Convolution sum
template<int N, class L, class BF>
static double convolution_sum(const vector &p, const L *lattice) {
auto sites = BF::template get_integer_support<N>();
lattice_site c = lattice->get_nearest_site(p);
lattice_site extent = lattice->get_dimensions();
double value = 0;
for(lattice_site s : sites) {
if(!lattice->is_lattice_site(c+s)) continue;
double w = BF::template phi<N>(p - (c+s).cast<double>());
if(w == 0.) continue;
value += w * (double)(*lattice)(c + s);
}
return value;
}This is slightly different from the above sum, but the concept is roughly the same
Generic Evaluation
Bringing this together in an example
using namespace sisl;
using namespace sisl::utility;
// Create a CC lattice
cartesian_cubic<float> data(7,7,7);
// Give it some data
data(2,1,3) = 1;
data(2,2,3) = 1;
data(4,1,3) = 1;
data(4,2,3) = 1;
data(1,4,3) = 1;
data(2,5,3) = 1;
data(3,5,3) = 1;
data(4,5,3) = 1;
data(5,4,3) = 1;
// Combine it with a basis function
si_function<cartesian_cubic<float>, // specify the lattice (and its data type)
tp_linear, // specify the basis function
3> // specify dimension
f_data(&data); // specify name and input lattice
// Most of the time we need to normalize the volume
// we can scale the input with the following code
vector scale(3);
// Scaling is in the form f(s*x, s*y, s*z), so we specify 7,7,7 as scale
scale << 7.,7.,7.;
f_data.set_scale(scale);
// To evaluate
f->eval(0.2, 0.1, 0.1);SISL
- Discrete filtering
- Filter inversion
- Resampling
- Quality metrics
- Fourier Transforms (map lattice to lattice)
Generic Evaluation
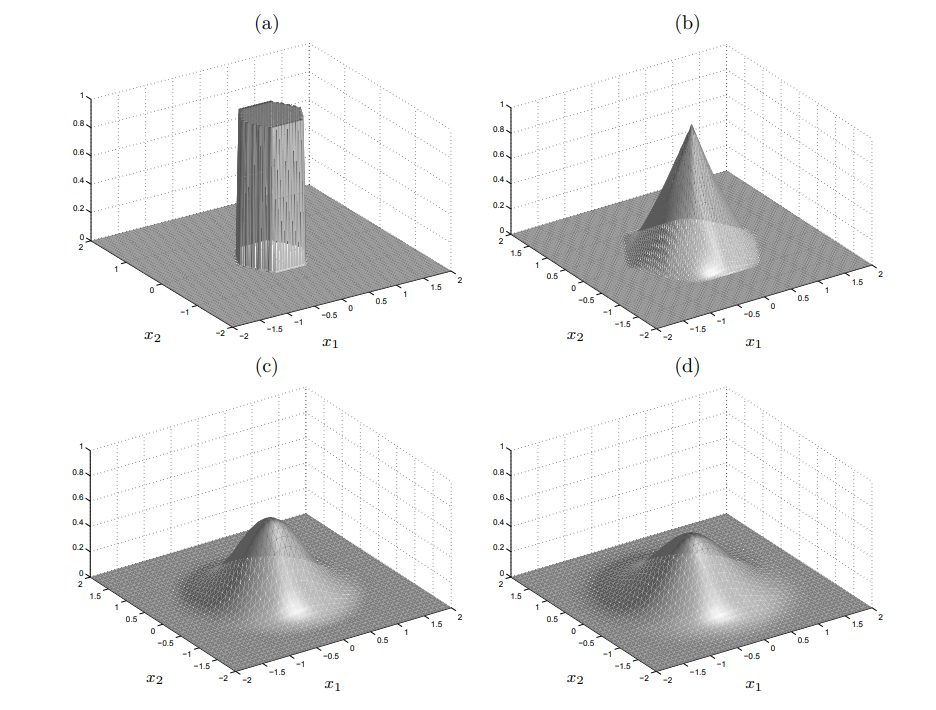
Built in Marching cubes (isovalue = 0.25)
Is this fast?
f(x) = \displaystyle\sum_{n\in\overline{supp(\phi(\cdot - x)} \cap \mathbb{Z}^3 }c_n \ \varphi(x-n) \chi_{L\mathbb{Z}^3}(n)
Sorta maybe fast... We can do better though
- Must evaluate \(\varphi\) a total of \(\overline{supp(\varphi(\cdot ))}\) times
- Particularly bad if \(\varphi\) is expensive to calculate
- For box splines, \(f(x)\) is locally a polynomial of some degree \(d\). We are doing multiple evaluations of \(\varphi\), then adding those values, which is also a polynomial of degree \(d\) locally.
Is this fast?
template<class T>
inline double __fast_cubic_tp_linear__(const vector &p, const cartesian_cubic<T> *lattice) {
//vector sx = lattice->get_dimensions().template cast<double>();
vector vox = p.array();// * sx.array();
int vx = (int)floor(vox[0]),
vy = (int)floor(vox[1]),
vz = (int)floor(vox[2]);
double x = vox[0] - (double)vx,
y = vox[1] - (double)vy,
z = vox[2] - (double)vz;
double v000 = (*lattice)(vx, vy, vz);
double v100 = (*lattice)(vx + 1, vy, vz);
double v010 = (*lattice)(vx, vy + 1, vz);
double v110 = (*lattice)(vx + 1, vy + 1, vz);
double v001 = (*lattice)(vx, vy, vz + 1);
double v101 = (*lattice)(vx + 1, vy, vz + 1);
double v011 = (*lattice)(vx, vy + 1, vz + 1);
double v111 = (*lattice)(vx + 1, vy + 1, vz + 1);
return (1.-x)*(1.-y)*(1.-z)*v000 +
x*(1.-y)*(1.-z)*v100 +
(1.-x)*y*(1.-z)*v010 +
x*y*(1.-z)*v110 +
(1.-x)*(1.-y)*z*v001 +
x*(1.-y)*z*v101 +
(1.-x)*y*z*v011 +
x*y*z*v111;
}
FAST_BASIS_SPECIALIZATION(tp_linear, cartesian_cubic, __fast_cubic_tp_linear__, 3, unsigned char);
FAST_BASIS_SPECIALIZATION(tp_linear, cartesian_cubic, __fast_cubic_tp_linear__, 3, char);
FAST_BASIS_SPECIALIZATION(tp_linear, cartesian_cubic, __fast_cubic_tp_linear__, 3, unsigned short);
FAST_BASIS_SPECIALIZATION(tp_linear, cartesian_cubic, __fast_cubic_tp_linear__, 3, short);
FAST_BASIS_SPECIALIZATION(tp_linear, cartesian_cubic, __fast_cubic_tp_linear__, 3, unsigned int);
FAST_BASIS_SPECIALIZATION(tp_linear, cartesian_cubic, __fast_cubic_tp_linear__, 3, int);
FAST_BASIS_SPECIALIZATION(tp_linear, cartesian_cubic, __fast_cubic_tp_linear__, 3, float);
FAST_BASIS_SPECIALIZATION(tp_linear, cartesian_cubic, __fast_cubic_tp_linear__, 3, double);Is this fast?
#ifndef NO_FAST_BASES //! if NO_FAST_BASES is defined, all fast implementations of basis functions will be disabled
#define FAST_BASIS_SPECIALIZATION(basis, lattice, function, dim, type) \
template<> \
inline double basis::convolution_sum<dim, lattice<type>, basis>(const vector &p, const lattice<type> *l) { \
return function<type>(p,l); \
}
#else
#define FAST_BASIS_SPECIALIZATION(basis, lattice, function, dim, type)
#endifIs this fast?
template<int N, class L, class BF>
static double convolution_sum(const vector &p, const L *lattice) {
auto sites = BF::template get_integer_support<N>();
lattice_site c = lattice->get_nearest_site(p);
lattice_site extent = lattice->get_dimensions();
double value = 0;
for(lattice_site s : sites) {
if(!lattice->is_lattice_site(c+s)) continue;
double w = BF::template phi<N>(p - (c+s).cast<double>());
if(w == 0.) continue;
value += w * (double)(*lattice)(c + s);
}
return value;
}Generic Evaluation
Built in marching cubes (isovalue = 0.25, fine step size)
| Normal Compile | -DNO_FAST_BASES |
|---|---|
| ~12s | ~405s |
Only running on one thread, same machine per run.
This is a BIG difference!
Aside
It's nice to be able to mix and match basis functions and lattices...
This generality comes at a price!
It's infeasible to derive fast code for every basis + lattice. The space of these is very large (infinite)
Compromise! For useful lattice+basis combinations, we can derive faster evaluation schemes, but leave in the generic evaluation schemes for experimentation
Fast Evaluation
Let's think about
f(x) = \displaystyle\sum_{n\in L\mathbb{Z}^3}c_n \ \varphi(x-n)
What would make this fast?
- Finite sum (compact basis functions)
- Small amount of terms
- Geometry of basis function
- Coset structure
Fast Evaluation
f(x) = \displaystyle\sum_{n\in L\mathbb{Z}^3}c_n \ \varphi(x-n)
=\displaystyle\sum^k_{i=1}\sum_{n\in G\mathbb{Z}^3}c_n \ \varphi\left(x-n-l_i\right)
=\displaystyle\sum^k_{i=1}\sum_{n\in C_i(x)} c_n \ \varphi\left(x-n\right)
Coset structure is a design parameter!
Define the set \(C_i(x)=(G\mathbb{Z}^3+l_i)\cap \overline{supp(\varphi(\cdot-x))}\)
Where \(G\) is the generating matrix for the coset decomposition.
Fast Evaluation
\displaystyle\sum_{n\in C_0(x)} c_n \ \varphi\left(x-n\right)
This allows us to treat the convolution as a sum of convolutions on different (shifted) grids, this is good for GPU implementations.
Now let's focus on how the geometry of the basis function affects reconstruction speed
- Take advantage of locality in texture memory
- Leverage existing tensor product hardware implementations in GPU
Fast Evaluation
Let's consider regions of space where the set
is constant. This depends on both the structure of the support of the basis function and chosen coset structure.
C_0(x)
A few examples...
Fast Evaluation
Tensor Product
Even
Odd
\Xi = \begin{bmatrix}
L & ... & L
\end{bmatrix}
L = \begin{bmatrix}
1 & 0 \\
0& 1
\end{bmatrix}
Fast Evaluation
Courant Element
\Xi = \begin{bmatrix}
1 & 0 & 1 \\
0& 1 & 1
\end{bmatrix}
L = \begin{bmatrix}
1 & 0 \\
0& 1
\end{bmatrix}
Fast Evaluation
ZP Element
\Xi = \begin{bmatrix}
1 & 0 & 1 & -1 \\
0& 1 & 1 & 1
\end{bmatrix}
L = \begin{bmatrix}
1 & 0 \\
0& 1
\end{bmatrix}
Fast Evaluation
Quincunx Lattice Example
L = \begin{bmatrix}
1 & -1 \\
1& 1
\end{bmatrix}
Fast Evaluation
Quincunx TP Element
\Xi = \begin{bmatrix}
2 & 0 & -2 & 0 \\
0& 2 & 0 & -2
\end{bmatrix}
L = \begin{bmatrix}
1 & -1 \\
1 & 1
\end{bmatrix}
1 coset
Fast Evaluation
Quincunx TP Element
\Xi = \begin{bmatrix}
2 & 0 & -2 & 0 \\
0& 2 & 0 & -2
\end{bmatrix}
L = \begin{bmatrix}
1 & -1 \\
1 & 1
\end{bmatrix}
2 cosets
G = \begin{bmatrix}
2 & 0 \\
0 & 2
\end{bmatrix}
l_1 = \begin{bmatrix}
0 \\
0
\end{bmatrix}
l_2 = \begin{bmatrix}
1 \\
1
\end{bmatrix}
Box Splines
\Xi = \begin{bmatrix}
1 & 0 & 1 & -1 \\
0& 1 & 1 & 1
\end{bmatrix}
Fast Evaluation
Representative sub-regions
\Xi = \begin{bmatrix}
1 & 0 & 1 & 1 \\
0& 1 & 1 & -1
\end{bmatrix}
L = \begin{bmatrix}
1 & 0 \\
0 & 1
\end{bmatrix}
Region of evaluation, \(R\).
\(\rho(x)\) is this shift
Fast Evaluation
Sub-regions
\(S_1\)
\(S_2\)
\(S_3\)
\(S_4\)
Fast Evaluation
So assume \(x\in R\). For each sub-region \(j\) we define \(\psi_j\) with
\displaystyle\sum_{n\in C_0(x)} c_n \ \varphi\left(x-n\right)
For box splines, we distribute the polynomial pieces into their corresponding sub-regions, i.e. \(\psi_i\). we can then spend time simplifying the polynomial \(\psi_i\)
= \Psi(x)
\Psi(x) := \begin{cases}
\psi_1(x) & x \in S_1 \\
\ & \vdots\\
\psi_M(x) & x \in S_M
\end{cases}
so that
Fast Evaluation
\(c_{0,0}\)
\(c_{1,0}\)
\(c_{1,1}\)
\(c_{0,1}\)
\(c_{-1,1}\)
\(c_{-1,0}\)
\(c_{-1,-1}\)
\(c_{0,-1}\)
\(c_{2,-1}\)
Fast Evaluation
\(c_{0,0}\)
\(c_{1,0}\)
\(c_{1,1}\)
\(c_{0,1}\)
\(c_{-1,1}\)
\(c_{-1,0}\)
\(c_{-1,-1}\)
\(c_{0,-1}\)
\(c_{2,-1}\)
\(C_0(R_1)\)
Fast Evaluation
\(c_{0,0}\)
\(c_{1,0}\)
\(c_{1,1}\)
\(c_{0,1}\)
\(c_{-1,1}\)
\(c_{-1,0}\)
\(c_{-1,-1}\)
\(c_{0,-1}\)
\(c_{2,-1}\)
\(C_0(R_2)\)
Fast Evaluation
\(c_{0,0}\)
\(c_{1,0}\)
\(c_{1,1}\)
\(c_{0,1}\)
\(c_{-1,1}\)
\(c_{-1,0}\)
\(c_{-1,-1}\)
\(c_{0,-1}\)
\(c_{2,-1}\)
\(C_0(R_3)\)
Fast Evaluation
\(c_{0,0}\)
\(c_{1,0}\)
\(c_{1,1}\)
\(c_{0,1}\)
\(c_{-1,1}\)
\(c_{-1,0}\)
\(c_{-1,-1}\)
\(c_{0,-1}\)
\(c_{2,-1}\)
\(C_0(R_4)\)
Fast Evaluation
Assume \(x\in R\). For fix some \(j\) we define \(\psi_j\) with
\psi_j(x) = \displaystyle\sum_{n\in C_0(S_j)} c_n \ \varphi\left(x-n\right)
We know that \(\varphi\) is a polynomial for all points \(x\in S_j\), so we can write it as
\psi_j(x) = \displaystyle\sum_{n\in C_0(S_j)} c_n \ P^j_n(x)
For some polynomial \(P_n(x)\)
Fast Evaluation
For the last example
\psi_1(x) = \displaystyle\sum_{n\in C_0(S_1)} c_n \ \varphi\left(x-n\right)
$$\psi_1=c_{-1,1}\varphi\left(x-(-1,1)\right) + c_{1,1} \varphi\left(x-(-1,1)\right)$$ $$ + c_{-1,0} \varphi\left(x-(-1,0)\right) + c_{1,0} \varphi\left(x-(1,0)\right) $$ $$ + c_{0,1} \varphi\left(x-(0,1)\right) + c_{0,0} \varphi\left(x-(0,0)\right)$$ $$ +c_{0,-1} \varphi\left(x-(0,-1)\right)$$
$$1/4(c_{-1,-1} + c_{-1,0} - 2c_{0,-1} - 2c_{0,0} + c_{1,-1} + c_{1,0})x_0^2 $$ $$+ 1/4(c_{-1,-1} - c_{-1,0} - 2c_{0,0} + 2c_{0,1} + c_{1,-1} - c_{1,0})x_1^2 $$ $$- 1/2(c_{-1,0} - c_{1,0})x_0 $$ $$+ 1/2((c_{-1,-1} - c_{-1,0} - c_{1,-1} + c_{1,0})x_0 - c_{0,-1} + c_{0,1})x_1 + 1/8c_{-1,0} $$ $$ + 1/8c_{0,-1} + 1/2c_{0,0} + 1/8c_{0,1} + 1/8c_{1,0})$$
$$\psi_1=$$
Fast Evaluation
We can explicitly calculate each region
$$\psi_3(x)=1/4(c_{-1,-1} + c_{-1,0} - 2c_{0,-1} - 2c_{0,0} + c_{1,-1} + c_{1,0})x_0^2 + 1/4(c_{-1,-1} - c_{-1,0} - 2c_{0,0} + 2c_{0,1} $$ $$+ c_{1,-1} - c_{1,0})x_1^2 - 1/2(c_{-1,0} - c_{1,0})x_0 + 1/2((c_{-1,-1} - c_{-1,0} - c_{1,-1} + c_{1,0})x_0 - c_{0,-1} + c_{0,1})x_1 $$ $$+ 1/8c_{-1,0}+ 1/8c_{0,-1} + 1/2c_{0,0} + 1/8c_{0,1} + 1/8c_{1,0}'$$
$$\psi_2(x)=1/4(2c_{-1,0} - c_{0,-1} - 2c_{0,0} - c_{0,1} + c_{1,-1} + c_{1,1})x_0^2 + 1/4(c_{0,-1} - 2c_{0,0} + c_{0,1} + c_{1,-1}$$ $$ - 2c_{1,0} + c_{1,1})x_1^2 - 1/2(c_{-1,0} - c_{1,0})x_0 + 1/2((c_{0,-1} - c_{0,1} - c_{1,-1} + c_{1,1})x_0 - c_{0,-1} + c_{0,1})x_1$$ $$ + 1/8c_{-1,0}+ 1/8c_{0,-1} + 1/2c_{0,0} + 1/8c_{0,1} + 1/8c_{1,0}$$
$$\psi_1(x)=1/4(c_{-1,0} + c_{-1,1} - 2c_{0,0} - 2c_{0,1} + c_{1,0} + c_{1,1})x_0^2 - 1/4(c_{-1,0} - c_{-1,1} - 2c_{0,-1} $$ $$+ 2c_{0,0} + c_{1,0} - c_{1,1})x_1^2 - 1/2(c_{-1,0} - c_{1,0})x_0 + 1/2((c_{-1,0} - c_{-1,1} - c_{1,0} + c_{1,1})x_0 $$ $$- c_{0,-1} + c_{0,1})x_1 + 1/8c_{-1,0} + 1/8c_{0,-1} + 1/2c_{0,0} + 1/8c_{0,1} + 1/8c_{1,0}$$
$$\psi_4(x)=1/4(c_{-1,-1} + c_{-1,1} - c_{0,-1} - 2c_{0,0} - c_{0,1} + 2c_{1,0})x_0^2 + 1/4(c_{-1,-1} - 2c_{-1,0} + c_{-1,1} + c_{0,-1} $$ $$- 2c_{0,0} + c_{0,1})x_1^2 - 1/2(c_{-1,0} - c_{1,0})x_0 + 1/2((c_{-1,-1} - c_{-1,1} - c_{0,-1} + c_{0,1})x_0 - c_{0,-1} + c_{0,1})x_1 $$ $$+ 1/8c_{-1,0} + 1/8c_{0,-1} + 1/2c_{0,0} + 1/8c_{0,1} + 1/8c_{1,0}$$
Fast Evaluation
Now what? We have a list of polynomials but there are still branches necessary, i.e.
\Psi(x) := \begin{cases}
\psi_1(x) & x \in S_1 \\
\ & \vdots\\
\psi_M(x) & x \in S_M
\end{cases}
This great on modern CPU architectures, but is not so good on GPU architectures. Multiple cases = branches.
Moreover, how do we determine which subregion we're in if we can't use branches?
Fast Evaluation
Sub-regions
\(S_1\)
\(S_2\)
\(S_3\)
\(S_4\)
1
0
2
0
| Index | Subreg |
|---|---|
| 0 | S_1 |
| 1 | S_2 |
| 2 | S_4 |
| 3 | S_3 |
Fast Evaluation
For the last example
$$=1/4(k_1 + k_2 - 2k_4 - 2k_5 + k_7 + k_8)x_0^2 $$ $$- 1/4(k_1 - k_2 - 2k_3 + 2k_4 + k_7 - k_8)x_1^2 $$ $$- 1/2(k_1 - k_7)x_0 + 1/2((k_1 - k_2 - k_7 + k_8)x_0 - k_3 + k_5)x_1$$ $$ + 1/8k_1 + 1/8k_3 + 1/2k_4 + 1/8k_5 + 1/8k_7$$
\(\psi^*(x_0,x_1, k_1, k_2, k_3, k_4,k_5,k_6,k_7)\)
Then
\psi_1(x) = \psi^*(x_0 , x_1 , c_{-1, 0}, c_{0, -1}, c_{0, 0}, c_{0, 1}, c_{1, -1}, c_{1, 0}, c_{1, 1})
\psi_2(x) = \psi^*(x_1 , x_0 , c_{0, -1}, c_{1, -1}, c_{-1, 0}, c_{0, 0}, c_{1, 0}, c_{0, 1}, c_{1, 1})
\psi_3(x) = \psi^*(-x_0 , -x_1 , c_{1, 1}, c_{1, 0}, c_{1, -1}, c_{0, 1}, c_{0, 0}, c_{0, -1}, c_{-1, 0})
\psi_4(x) = \psi^*(-x_1 , -x_0 , c_{1, 1}, c_{0, 1}, c_{1, 0}, c_{0, 0}, c_{-1, 0}, c_{1, -1}, c_{0, -1})
We only need to know one polynomial!
Fast Evaluation
\(c_{0,0}\)
\(c_{1,0}\)
\(c_{1,1}\)
\(c_{0,1}\)
\(c_{-1,1}\)
\(c_{-1,0}\)
\(c_{-1,-1}\)
\(c_{0,-1}\)
\(c_{2,-1}\)
\(C_0(R_2)\)
Fast Evaluation
\(c_{0,0}\)
\(c_{1,0}\)
\(c_{1,1}\)
\(c_{0,1}\)
\(c_{-1,1}\)
\(c_{-1,0}\)
\(c_{-1,-1}\)
\(c_{0,-1}\)
\(c_{2,-1}\)
\(C_0(R_1)\)
Fast Evaluation
There is no guarantee that we'll only have one \(\psi^*\), so we may have a set of such functions. We want to find a minimal set of \(\{\psi^*_j\}\), that contains the set \(\{\psi_1 \cdots \psi_M\}\) under rotations and translations of the elements of \(\{\psi_j^*\}\)
Rotations and translations can be stored in a lookup table for GPU evaluation.
Minimize the amount of elements \(\{\psi_j^*\}\) has, since having multiple leads to either branching or additional wasted work on the GPU
Fast Evaluation
Finding correspondances -- let's backtrack to
\psi_j(x) = \displaystyle\sum_{n\in C_0(S_j)} c_n \ P^j_n(x)
If I have some rotation \(\bm{R}\) (and maybe translation \(\bm{t}\))
Then \(P_n^i(x) = P^j_{\bm{R}n}(\bm{R}^{-1}(x-\bm{t}))\)
So we just take t to be the center of each region's lookup pattern, and R to be an element of the symmetry group for the spline
Fast Evaluation
How do we evaluate the polynomials?
Recall Horner's method
f(x) = \displaystyle\sum^n_{k=1} a_k x^k = a_0 + a_1x + \cdots + a_{n-1}x^{n-1} + a_nx^n
f(x) = \displaystyle\sum^n_{k=1} a_k x^k = a_0 x(a_1 + ... + x(a_{n-1} + a_nx))
There is no such unique factorization with more than one variable
Fast Evaluation
That's fine, Horner factorization still exist, we could just brute force search for them
f({x}) = c_1x_1x_2x_3x_4 + c_2x_2x_3x_4x_5 + c_3x_1x_3x_4x_5 + c_4x_1x_2x_4x_5 + c_5x_1x_2x_3x_5 + c_6
f({x}) = x_3x_4(x_2(c_1x_1+c_2x_5) + c_3x_1x_5) + x_1x_2x_5(c_4x_4 + c_5x_3) + c_6
12 muliplications
However, there's a tradeoff -- this requires more intermediate results to be stored, therefore it increases GPU register use...
Greedy has fixed register use...
Lerp Trick
Linear texture fetches are fast in hardware
In 1D, if we have adjacent samples on a grid
\(\psi(x) = \cdots + c_i P_i(x) + c_{i+1} P_{i+1}(x) + \cdots \)
It's possible to define functions \(g(x)\) and \(h(x)\) such that
\(c_i P_i(x) + c_{i+1} P_{i+1}(x) = g(x)LERP(c_i, c_{i+1}, h(x)) \)
LERP is implemented in hardware, and this can be extended into groups of 4 points in 2D ( and 4 and 8 in 3D)
Set Covering
Set Covering
Set Covering
This is actually a difficult problem, but can be solved with Algorithm X
Ordering Lookups
Solve TSP (hamiltonian path, actually) on graph that records the cache misses going between lookups
Fast Evaluation
General outline
result = 0
for each coset j:
n = rho(x)
x = x - n
sub_reg_idx = planeLookup(x)
R = localTransformLookup[sub_reg_idx]
t = localTranslateLookup[sub_reg_idx]
x = R.inverse()*(x - t)
result = 0
for each group of lattice sites:
compute g(x) and h(x)
c = linear texture fetch
result += c*g
return fCode Generation
Spent a lot of time trying to use Jinja (think Django templates) with CUDA
Many different cases:
- Linear interpolation/no linear interpolation
- Multiple reference subregions? Branch predication
- Branch pred + linear interpolation?
- What about if there's only one subregion?
Spent a lot of time making small changes, regenerating code, compiling and testing...
Spent more time breaking things....
Code Generation
One full codebase re-write later, LLVM IR (Low Level Virtual Machine Intermediate Representation) appears to be the winning solution.
Advantages:
- Platform agnostic(-ish), write once and port to different architectures easily. Some architectures expose intrinsics to speed up computation, so need multiple cases for that
- JIT code, compile, and link into Python context i.e. fast iteration when debugging
- Low-level primitives --- feels like an assembly programming language, better control
- Many optimization passes available
Code Generation
One full codebase re-write later, LLVM IR (Low Level Virtual Machine Intermediate Representation) appears to be the winning solution.
Disadvantages:
- Emitting PTX code is a huge pain --- ptxas is difficult to use and statically link with existing CUDA. But it's doable
Other than that, this is clearly the more elegant solution
Overview
Spline
Unrolled conv sum representation
LLVM IR
x86_64
PTX
Analysis
other
Codegen
\(\vdots\)
Thanks!
Experiments
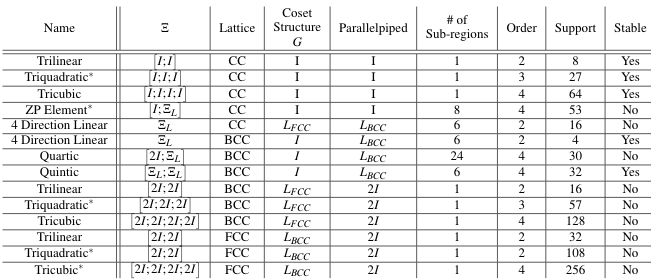
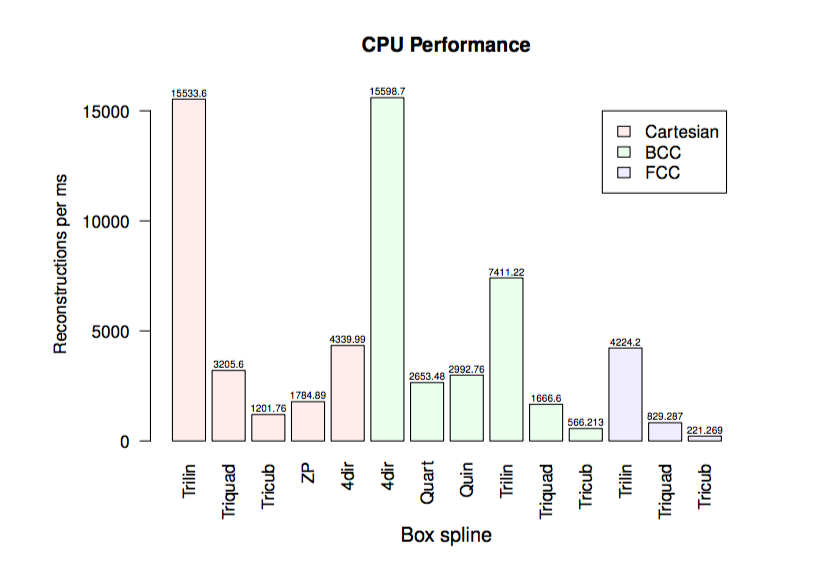
CPU Performance, GPU Performance, Volumetric Rendering
Results
Results
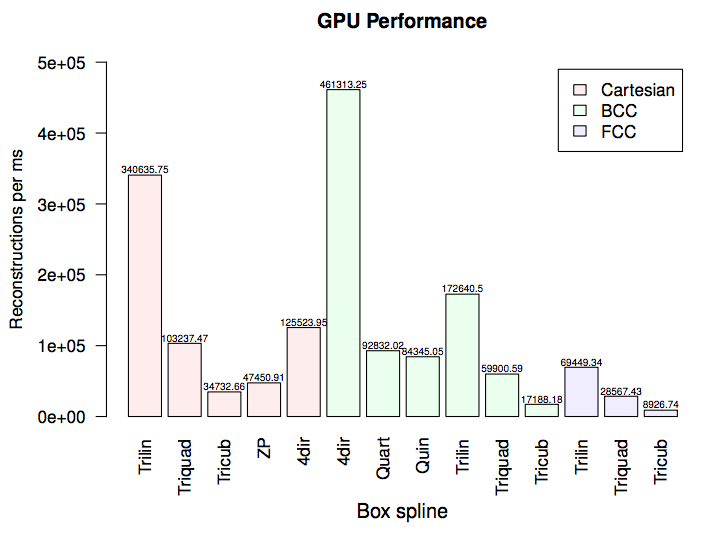
No hardware acceleration*
Experiments
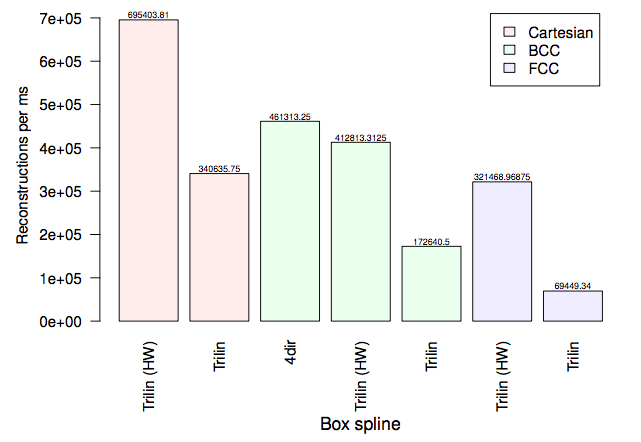
Results
Volume Rendering
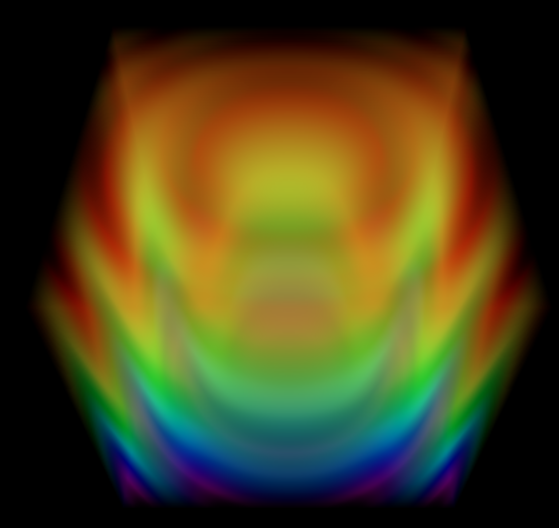
Results
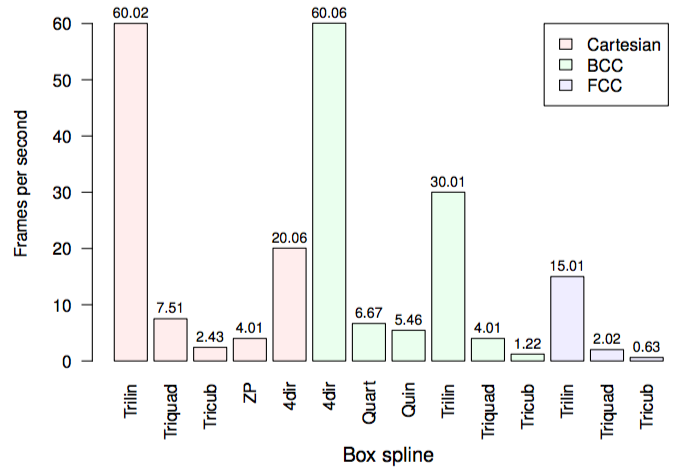
Results
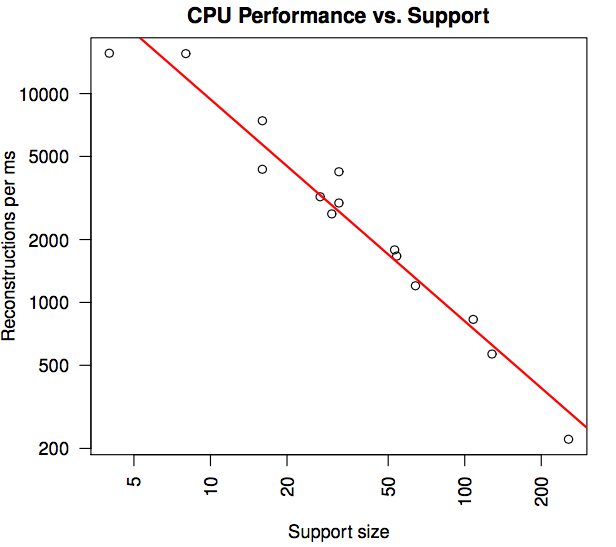
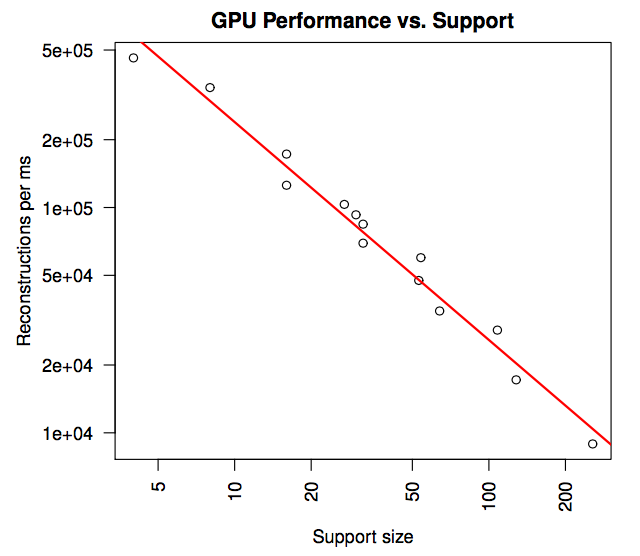
Conclusion
This allows us to build a general interpolation library, on regular grids, that is well suited to experimentation and speed
Lots of stuff I haven't talked about
- Filtering
- Fourier Transforms
- Compression
Fast Splines
By Joshua Horacsek
