Fourier Transform
Recall: \(L_p(S, \Sigma, \mu)\) is a Banach space, and \(L_2(S,\Sigma, \mu)\) is a Hilbert space with inner product \[ \langle f,g \rangle = \int_Sf(x)\bar{g}(x) \ d\mu(x).\]
Convolution Algebra
Definition: Let \(f\) and \(g\) be measurable functions on \(\mathbb{R}\), we define the convolution between \(f\) and \(g\) as \[(f*g)(s) := \int_\mathbb{R}f(t)g(s-t) \ dt\] for values \(s\) at which this integral converges.
Example: The uniform B-splines are given by successive convolutions with the box function
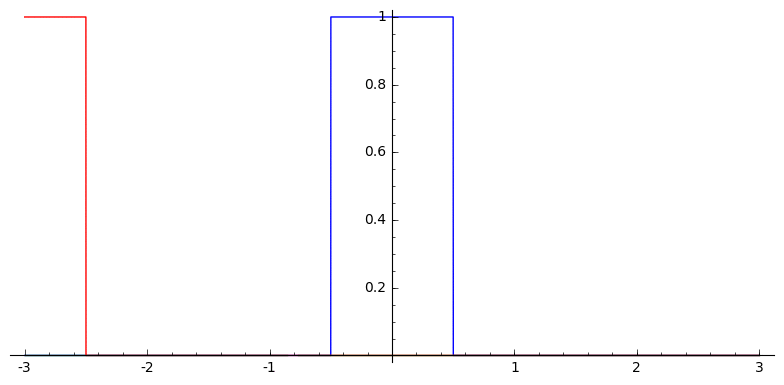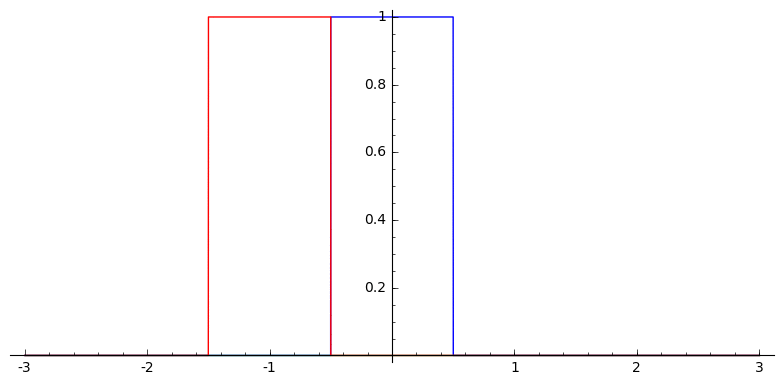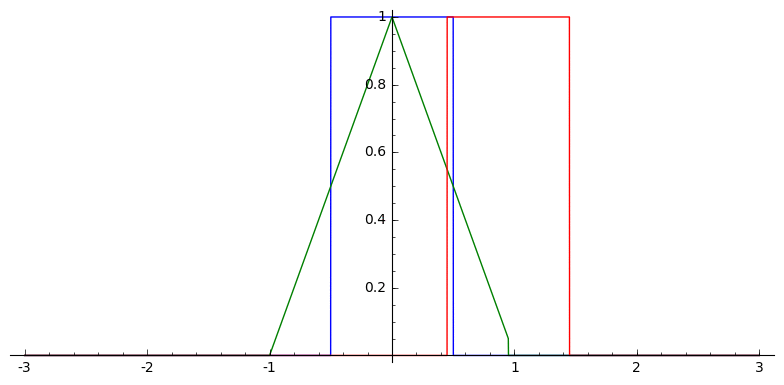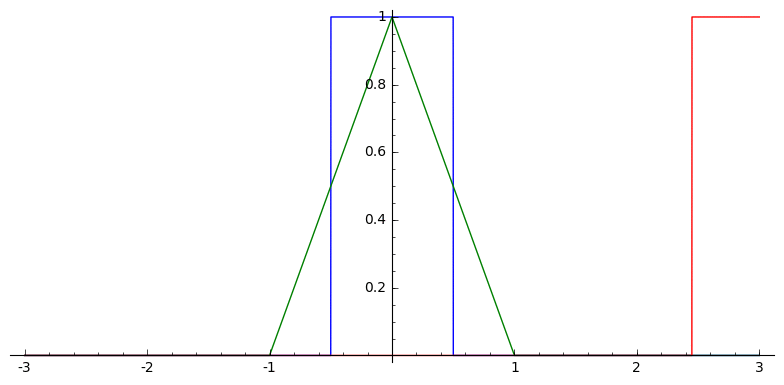
Proposition:
- If \(f\) and \(g\) are measurable functions on \(\mathbb{R}\) then \(f*g = g*f\)
- If \(f\in L_1(\mathbb{R})\) and \(g\in L_p(\mathbb{R})\) for \(1 \leq p \leq \infty\) then \[\|f*g\|_p \leq \|f\|_1 \cdot \|g\|_p\]
- The convolution operation is distributive. That is, for \(f\in L_1(\mathbb{R})\) \(g,h \in L_{p}(\mathbb{R})\) and \(a\in \mathbb{C}\) we have \[f*(a\cdot g + h) = a\cdot f*g + f*h\] with both \(f*(a\cdot g + h)\) and \(a\cdot f*g + f*h\) in \(L_{p}(\mathbb{R})\).
- The convolution operation is associative. That is, for \(f,g \in L_1(\mathbb{R})\) and \(h \in L_{p}(\mathbb{R})\)we have\[(f*g)*h = f*(g*h)\] with both \((f*g)*h\) and \(f*(g*h)\) in \(L_p(\mathbb{R})\)
Proposition:
The vector space over \(L_1(\mathbb{R})\) with norm \(\|\cdot\|_1\) and binary operation \(*\) forms a non-unital Banach algebra.
Definition:
The convolution operator is defined as
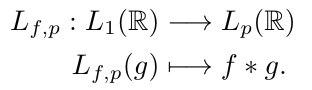
Note: This is linear and bounded, i.e. \(L_{f,p} \in B(L_p(\mathbb{R})\))
Definition: The image of \({L}_2(\mathbb{R})\) under \(L_{f,2}\) is denoted \(\mathcal{A}_1\), and the normed closure of \(\mathcal{A}_1\) is denoted \(\mathcal{U}_1\).
Note:
For each function \(f\in L_1(\mathbb{R})\), we have \[\|L_{f,2}-I\|\geq \frac{1}{2}\] so \(I\notin \mathcal{U}_1\).
Proposition:
The linear space \(\mathcal{U}_0\) is a norm-closed commutative algebra of operators on \(L_2(\mathbb{R})\) and \(\mathcal{U}_1\) is a proper maximal ideal in \(\mathcal{U}_0\).
Definition:
The linear space generated by \(I\) and \(\mathcal{U}_1\) is denoted \(\mathcal{U}_0\).
Lemma:
If \((u_n)_{n=1}^\infty\) is a sequence of positive functions in
\(L_1(\mathbb{R})\) such that \(\|u_n\|_1=1\) and \(u_n(t)=0\) when \(t\notin [-\frac{1}{n}, \frac{1}{n}]\), then \(\|f*u_n-f\|_p\to0\) for each \(f\in L_{p}(\mathbb{R})\).
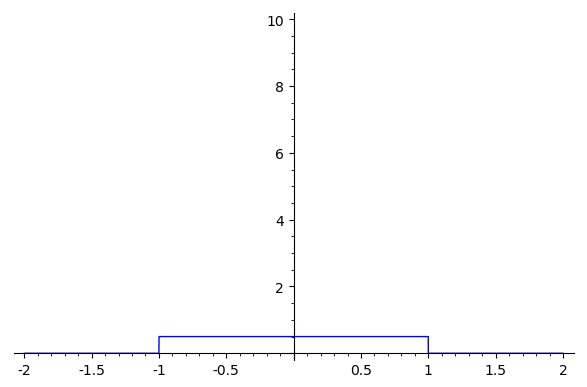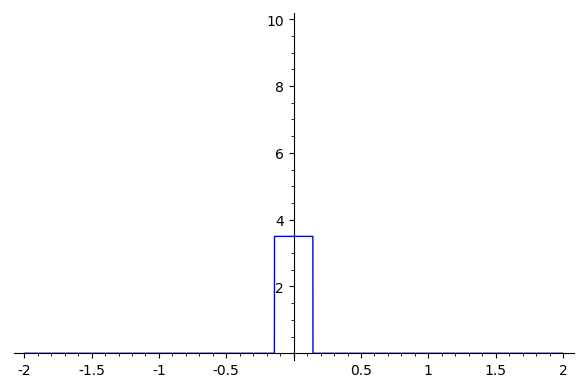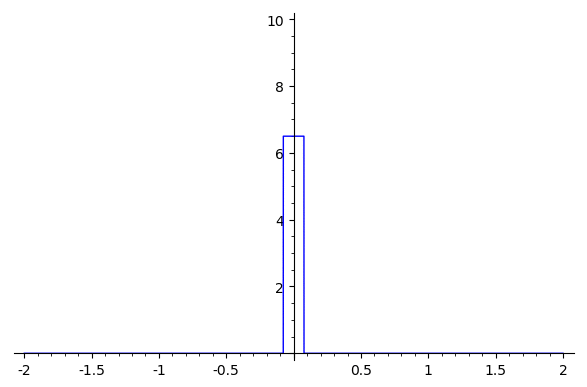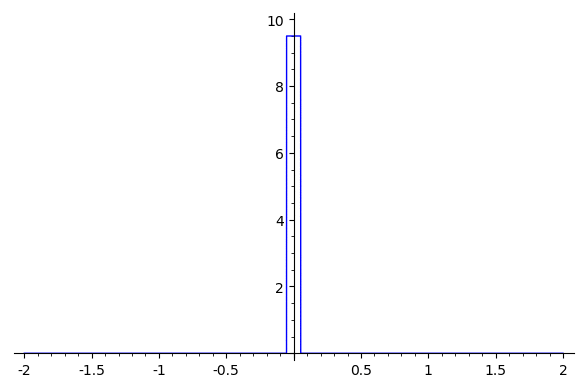
Note/Example:
If we take \(f^*(s)= \bar{f}(-s)\), and take \(g,h\in L_2(\mathbb{R})\), then \[L_{f^*,2}=L^*_{f,2}\]
Thus, \(\mathcal{A}_1, \mathcal{U}_1\) and \(\mathcal{U}_0\) contain \(L^*\) when they contain \(L\).
So, \(\mathcal{U}_0\) is a unital C*-algebra.
Fourier Transform on \(L_1(\mathbb{R})\)
Lemma:
For each \(r\in \mathbb{R}\), the equation \[\xi_r(t) = e^{2\pi itr}\] defines a character of \(\mathbb{R}\). The mapping is an isomorphism of \(\mathbb{R}\) onto \(\hat{\mathbb{R}}\).
Theorem:
a non zero linear functional \(\rho\) on \(L_1(\mathbb{R})\) is multiplicative if and only if there is a unique \(r\in\mathbb{R}\) such that \[\rho(f) = \hat{f}(r) := \int f(t)e^{2\pi itr} \ dt.\]
Definition: The dual group \(\mathbb{\hat{R}}\) contains the characters of \(\mathbb{R}\) onto the group \(\mathbb{T}_1\).
Theorem:
There is a homeomorphism \(\Lambda\) of \(\mathcal{M}_0(\mathbb{R})\) onto \(\mathbb{R}\) such that, if \(\rho_0\in \mathcal{M}_0(\mathbb{R})\), and \(r=\Lambda(\rho_0)\), then \[\rho_0(L_{f,1})=\hat{f}\] for each \(f\in L_1(\mathbb{R})\).
Definition: \(\mathcal{M}_0\) is the space of non-zero multiplicative linear functionals on \(\mathcal{U}_0\).
Definition: The function \(\hat{f}\) is known as the Fourier transform of \(f\)
Corollory : The Fourier transform \(\hat{f}\) of a function \(f\in L_1(\mathbb{R})\) has the following properties:
- For \(f,g\in L_1(\mathbb{R})\) then \(\widehat{f+g} = \hat{f} + \hat{g}\)
- The Fourier transform is unique
- \(\hat{f}\) vanishes at \(\pm \infty\)
- \(\|\hat{f}\|_\infty \leq \|f\|_1\) and \(\hat{f}\) is continuous
- \(\widehat{f*g} = \hat{f}\cdot\hat{g}\)
- Shift property: \(\widehat{f(\cdot - h)} = \hat{f}e^{2\pi i h r}\) and \(\widehat{fe^{2\pi i h x}} = \hat{f}(\cdot-h) \)
- Scale property: \(\widehat{f(ax)} = \frac{1}{|a|}\hat{f}(\frac{r}{a})\)
- Derivative property: \(\widehat{f^\prime} = 2\pi i r \hat{f}\)
Schwarz Class and Tempered Distributions
Definition: A function \(f\) belongs to the Schwartz Class \(\mathcal{S}\) if it is infinitely differentiable and \[\sup_x |x^a f^{(b)}(x)| < \infty\] for \(a,b \in \mathbb{N}\). I.e. its derivatives decrease rapidly at infinity.
Note: The Schwartz class is a subset of \(L_1(\mathbb{R})\) and is dense in \(L_p(\mathbb{R})\).
Definition: The space of linear functionals in \(\mathcal{S}^*\) is called the space of tempered distributions.
Theorem: The Fourier transform is a continuous map from \(\mathcal{S}\) to \(\mathcal{S}\) such that \[\int_\mathbb{R}f \hat{g}= \int_\mathbb{R}\hat{f} g\] and \[f(x) = \int_\mathbb{R}\hat{f}(r)e^{2\pi i x r} dr.\]
Corollary: For \(f\in \mathcal{S}\), \(\widehat{(\hat{f})}=\tilde{f} \) where \(\tilde{f}(x)=f(-x)\), thus the Fourier transform on \(\mathcal{S}\) has period 4.
Definition: The Fourier transform of \(T\in S^*\) is the tempered distribution \(\hat{T}\) given by \[\hat{T}(f)=T(\hat{f}), \ f \in \mathcal{S}. \]
Theorem: The Fourier transform is a bounded linear bijection from \(S^*\) to \(S^*\) whose inverse is also bounded.
Fourier Transform on \(L_2(\mathbb{R})\)
Theorem: The Fourier transform for \(f\in L_2(\mathbb{R})\) is \[\hat{f}(r)=\lim_{t \to \infty}\int^t_{-t}f(x)e^{-2\pi i x r} \ dx \] and we have \(\hat{f}\in L_2(\mathbb{R}) \) and \[{f}(x)=\lim_{t \to \infty}\int^t_{-t}\hat{f}(r)e^{2\pi i x r} \ dr. \]
Theorem: For \(f \in L_2(\mathbb{R})\), we have \(\|f\|_2=\|\hat{f}\|_2\).
Corollary: The Fourier transform is an isometry on \(L_2(\mathbb{R})\)
Fourier Transform
By Joshua Horacsek
Fourier Transform
- 1,046



