Parallel  Numerical Methods

Iterative Methods, Conjugate Gradient, and Preconditioning

Roadmap

  • Iterative Methods
  • Steepest Descent and Conjugate Gradient
  • GMRES
  • Multigrid

Let's retread some ground to get a better feel for some of the algorithms we've investigated so far

Sparse Matrices

Saving space and time

  • An  \(n \times m\) matrix uses \(O(nm)\) storage 
  • Matrix vector multiplication costs \(O(nm)\) for \(n \times m\) matrices 
  • Many of problems correspond to matrices with many zero entries (or are banded/structured in some way)
  • We consider these matrices to be sparse, generally we think of a matrix as sparse when the ratio of zeros to non-zeros is greater than \(\frac{1}{2}\)
  • Why store zeros?

Sparse Matrices

Saving space and time

  • Useful for matrices that are so large that they cannot fit in memory
  • How do you store these matrices (data structures)?
\begin{bmatrix} 1 & 2 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 3 & 4 & 0 \\ 0 & 0 & 0 & 6 & 0 \\ 0 & 0 & 0 & 7 & 1 \end{bmatrix}

Sparse Matrices

Saving space and time

Set of triplets

\begin{bmatrix} 1 & 2 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 3 & 4 & 0 \\ 0 & 0 & 0 & 6 & 0 \\ 0 & 0 & 0 & 7 & 1 \end{bmatrix}
i j value
1 1 1
2 1 2
2 2 1
3 3 3
4 3 4
4 4 6
4 5 7
5 5 1

Bad for iterating over rows/columns

Fast lookup, \(O(m)\) storage

Sparse Matrices

Saving space and time

Linked Representation

\begin{bmatrix} 1 & 2 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 3 & 4 & 0 \\ 0 & 0 & 0 & 6 & 0 \\ 0 & 0 & 0 & 7 & 1 \end{bmatrix}

1

2

1

4

3

6

7

1

Sparse Matrices

Saving space and time

Compressed Sparse Row

Stores three non-zero arrays

\begin{bmatrix} 1 & 2 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 3 & 4 & 0 \\ 0 & 0 & 0 & 6 & 0 \\ 0 & 0 & 0 & 7 & 1 \end{bmatrix}

A=[1 2 1 3 4 6 7 1]

IA=[0 2 3 5 6 8]

JA=[0 1 1 2 3 3 3 4]

A = non zero columns of the matrix

IA = number of nonzero elements on the (i-1)-th row in the original matrix

JA = index of the column for an element in A

Sparse Matrices

Saving space and time

Compressed Sparse Row

A=[1 2 1 3 4 6 7 1]

IA=[0 2 3 5 6 8]

JA=[0 1 1 2 3 3 3 4]

A = non zero columns of the matrix

IA = number of nonzero elements on the (i-1)-th row in the original matrix

JA = index of the column for an element in A

def sparse_matrix_mult(n, A, IA, JA, x):
    Ax = x.copy()*0
    a_idx = 0
    for i in range(n):
        num_elements = IA[i + 1] - IA[i] 
        for _ in range(num_elemnets):
            Ax[i] += x[JA[a_idx]] * A[a_idx]
            a_idx += 1
    return Ax

Sparse Matrices

Saving space and time

Related Friends

\begin{bmatrix} 1 & 2 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 3 & 4 & 0 \\ 0 & 0 & 0 & 6 & 0 \\ 0 & 0 & 0 & 7 & 1 \end{bmatrix}
  • List of keys
  • Compressed Sparse Columns
  • Variations on CSR

Sparse Matrices

Saving space and time

 

  • If a matrix has \(m\) non zero entries, then matrix vector multiplication is \(O(mn)\)
  • Direct methods on sparse matrices?
  • Factorizations can produce dense matrices, how do you store those?

Matrix Free Representations

An aside

What if you have no explicit matrix \(A\), but only a procedure that calculates \(Ax\) for a given \(x\) ?

Iterative Methods

Can massively outperform direct methods, especially when convergence is fast 

Stationary

Krylov Subspace methods

Jacobi, Gauss seidel

  • Iterative methods for solving linear system \(Ax = b\) begin with initial guess for solution and successively improve it until solution is as accurate as desired
  • In theory, infinite number of iterations might be required to converge to exact solution
  • Iteration terminates when residual \(\|b − Ax\|\), or some other measure of error is as small as desired Iterative methods are especially useful when matrix A is sparse

Non-stationary

Power Iteration

Simplest method for computing one eigenvalue-eigenvector pair is power iteration, which in effect takes successively higher powers of matrix times initial starting vector

for k in range(iterations):
	y = A.dot(x)
	x = y/y.infty_norm()

Stationary

Iterate on vector 

Why do these methods work? Also, when?

\(x^{new} = Tx^{old} + c\) 

T never changes

Jacobi and Gauss Siedel

\(x^*_i = \frac{b_i - \sum_{i\ne j} a_{i,j}x_j}{a_{ii}}\)

Beginning with an initial guess, both methods compute the next iterate by solving for each component of \(x\) in terms of other components of \(x\)

If D, L, and U are diagonal, strict lower triangular, and strict upper triangular portions of A, then Jacobi method can be written

\(x^* = D^{-1}(b-(L+U)x)\)

\(x^*_i = \frac{b_i - \sum_{j<i} a_{i,j}x^*_j -\sum_{j>i} a_{i,j}x_j}{a_{ii}}\)

 

\(x^* = (L+D)^{-1}(b-Ux)\)

Jacobi and Gauss Siedel

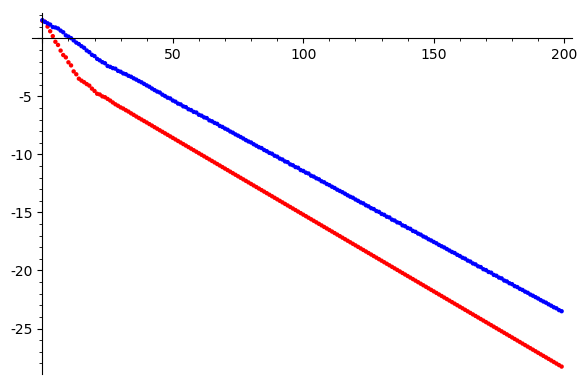
Convergence

Take a random \(100 \times 100\) matrix and solve for a random vector

\(\log \|Ax-b\|\)

Iterations

Gauss Seidel

 Jacobi

Pre-preconditioners

A first introduction, sorta

Change problem slightly so that it's easier to solve. 

\(x^*_i =(1-\omega)x^*_i + \omega\left(\frac{b_i - \sum_{j<i} a_{i,j}x^*_j -\sum_{j>i} a_{i,j}x_j}{a_{ii}}\right)\)

 

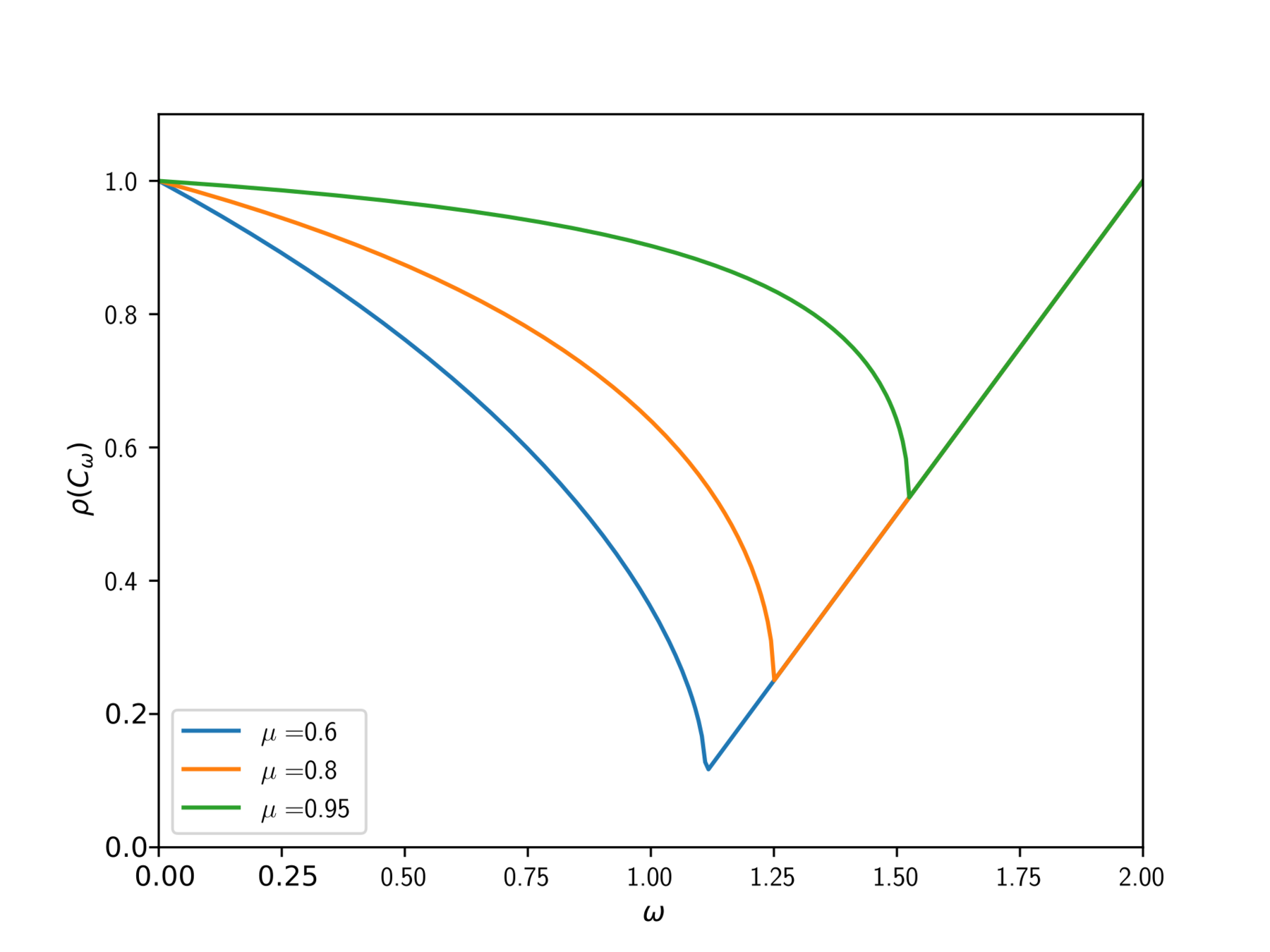
Pre-preconditioners

A first introduction, sorta

Change problem slightly so that it's easier to solve. 

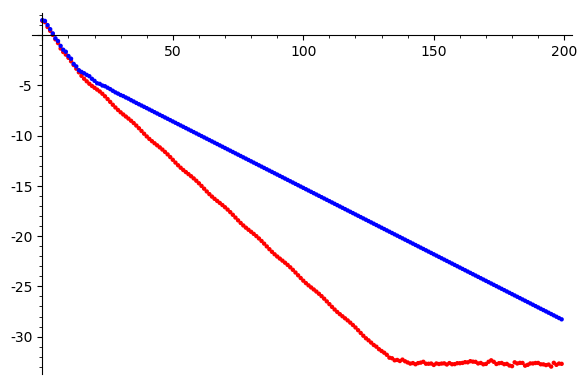
Iterations

Gauss Seidel

Gauss Seidel SOR \(\omega=0.95\)

\(\log \|Ax-b\|\)

Steepest Descent

\(\displaystyle\argmin_x \frac{1}{2}x^TAx - x^Tb\)

Obtains minimum when \(Ax=b\)

Steepest descent \(x^*=x + \alpha\nabla(\frac{1}{2}x^TAx - x^Tb)\)

 

\(\alpha = r^Ts/(s^TAs)\)

\(r:= b - Ax\)

If A is \(n \times n\) symmetric positive definite matrix, we minimize the quadratic form

Optimal line search parameter

Steepest Descent

def steepest_descent(A, b, max_iters = 1000):
    x = np.array([0.0] * A.shape[0])
    for _ in xrange(max_iters):
        r = b-A.dot(x)
        s = r.dot(r)
        a = s/(r.dot(A.dot(r)))
        if s < 1e-10:
            break
        x = x+a*r
    print("%d iterations" % _ )
    return x, r

Steepest Descent

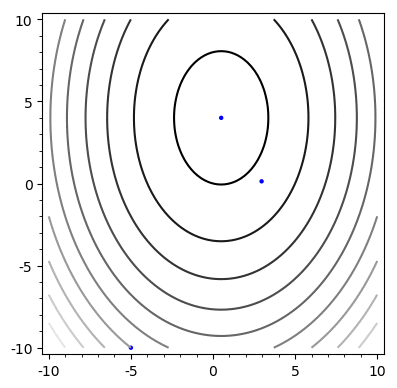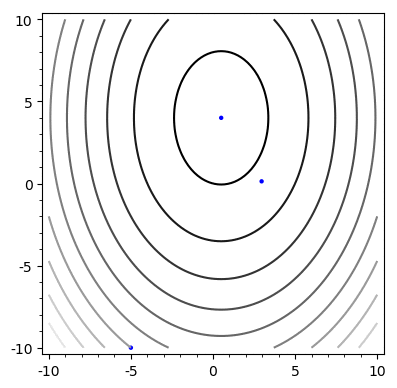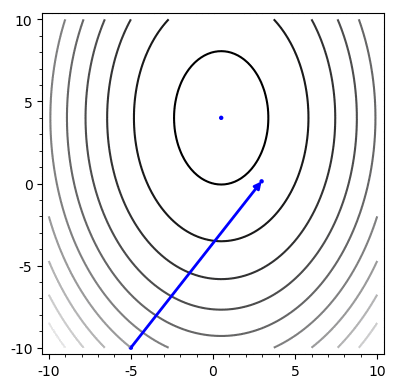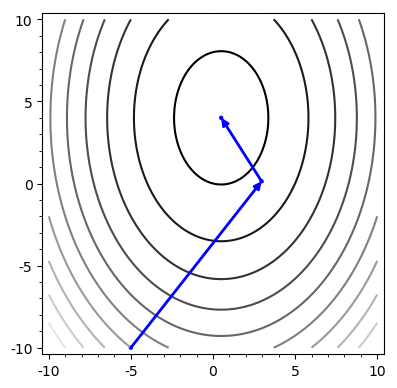
Example

A = \begin{bmatrix} 2 & 0 \\ 0 & 1 \end{bmatrix}
b = \begin{bmatrix} -1 \\ 5 \end{bmatrix}

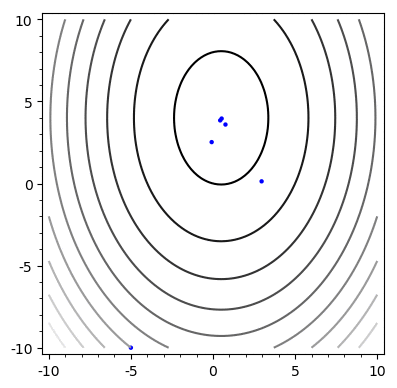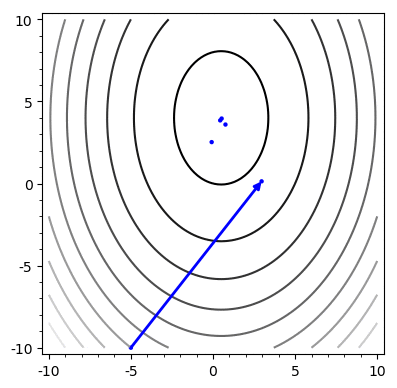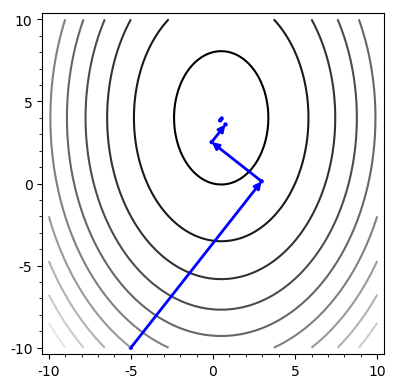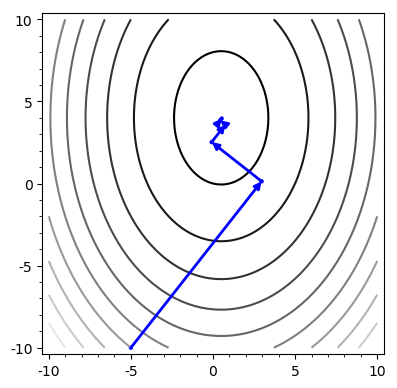
Problem: Chooses the same vector more than once

Conjugate Gradient

Fixing steepest descent by choosing gradients in new, orthogonal, directions

Krylov Subspaces

\( K_n = \{b, Ab, A^2b, \cdots A^{n-1}b\}\)

General idea

Seek solutions in the space

That is, at step \(n\) look for a solution \(x_n\) such that

\(\displaystyle\min_{x_n \in K_n} \|b-Ax_n\|\)

Why find a solution in \(K_n\)?

Krylov Subspaces

General idea

\(0 = q(A)\)

\(0 = \displaystyle\sum_{i=0}^m a_iA^i\)

\(0 = a_0I + \displaystyle\sum_{i=1}^m a_iA^i\)

\(I =  - \displaystyle\sum_{i=1}^m \frac{a_i}{a_0}A^i\)

\(A^{-1} =  - \displaystyle\sum_{i=1}^m \frac{a_i}{a_0}A^{i-1}\)

\(A^{-1}b =  - \displaystyle\sum_{i=1}^m \frac{a_i}{a_0}A^{i-1}b\)

\(x = A^{-1}b \in K_m\) 

\(q(\cdot)\) is the minimal polynomial for A

\(m\) depends on the structure of the eigenvalues of \(A\)

Conjugate Gradient

Fixing SD by choosing gradients in new, unique directions

Each sucessive \(p_i\) is chosen to be orthogonal to the set \(\{p_0, \cdots, p_{i-1}\}\)

As the algorithm progresses, \(p_i\) and \(r_i\) span the same Krylov subspace.

 \(x_k\)can be regarded as the projection of \(x\) on \(K_k\).

If \(m << n\), then we converge in few iterations. If we allow \(k\to n\) then we have a direct method.

Conjugate Gradient

def conjgrad(A, x, b):
    r = b - A.dot(x)
    p = r.copy()
    rsold = r.dot(r)
    e = []

    for i in range(len(b)):
        Ap = A.dot(p);
        alpha = rsold / (p.dot(Ap))
        x = x + alpha * p;
        r = r - alpha * Ap;
        rsnew = r.dot(r);
        p = r + (rsnew / rsold) * p;
        rsold = rsnew;
        e += [sqrt(rsnew)]
    return x, e

Conjugate Gradient

A = \begin{bmatrix} 2 & 0 \\ 0 & 1 \end{bmatrix}
b = \begin{bmatrix} -1 \\ 5 \end{bmatrix}

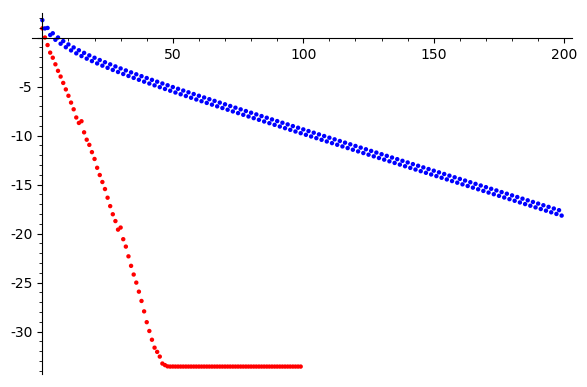
Convergence

Iterations

Steepest Desc

Conj Grad

\(\log \|Ax-b\|\)

Problems

What if A isn't positive definite? What if A isn't symmetric?

Generalised Minimal Residual

\( K_n = \{b, Ab, A^2b, \cdots A^{n-1}b\}\)

Again, for an \(m\times m\) matrix \(A\) seek solutions in the space

That is, at step \(n\) look for a solution \(x_n\) such that

\(\displaystyle\min_{x_n \in K_n} \|b-Ax_n\|\)

Iteratively build up an orthogonal basis for \(K_n\) (QR decomposition) which allows us to easily solve for a given \(x_n\)

Use Arnoldi  iteration to build \(Q_n\) and \(H\) such that \(AQ_n = Q_{n+1}H\) (H is Hassenberg, i.e almost upper triangular)

Arnoldi Iteration

Start with an arbitrary vector \(q_1\) with norm 1.

For k = 2, 3, …

  • \(q_k = Aq_{k-1}\)
  • for j in 1 to k-1
    • \(h_{j,k} = q_j^*q_k\)
    • \(q_k = q_k-h_{j,k}q_j\)
  • \(h_{k,k-1} = \|q_k\|\)
  • \(q_k = q_k/h_{k,k-1}\)

Can be built up incrementally

Generalised Minimal Residual

Use Arnoldi  iteration to build \(Q_n\) and \(H\) such that \(AQ_n = Q_{n+1}H\) (H is Hassenberg, i.e almost upper triangular)

\(\|Ax_n - b\| = \|Q_{n+1}^TAx_n - Q_{n+1}^Tb\| = \|Q_{n+1}^TAQ_ny_n - Q_{n+1}^Tb\| = \|H_ny_n - \beta e_1\|\)

 
 

with \(\beta = \|b-Ax\|\)

So the algorithm is as follows, on the \(n^{th}\) iteration

  1. Calculate \(q_{n}\) with the Arnoldi method;
  2. Find the \(y_n\)  which minimizes \(\|H_ny_n - \beta e_1\|\)
  3. Compute \(x_{n}=Q_{n}y_{n}\)
  4. Repeat if the residual is not yet small enough.

Since \(x\in K_n\) and \(Q_n\) is a basis for \( K_n\)

Preconditioners

Make a given problem easier

Instead of solving \(Ax = b\), we solve a related problem \(AM^{-1}y = b\) for \(y\), then compute \(x = My\)

  • The matrices \(M\) and \(M^{-1}\) should be easily expressible
  • The matrix \(AM^{-1}\) should be better conditioned than \(A\)

Preconditioners

Incomplete LU factorization

Since LU of  sparse matrix may be dense, seek a sparse approximation to LU factorization.

Start by noting all the non-zero elements of an \(n \times n\) sparse matrix \(A\).

\(G(A) = \{(i,j) | A_{ij} \ne 0\}\)

Then choose a sparsity pattern \(S\) such that 

\(S\subset \{1, \cdots, n\}^2, \ \ G(A) \subset S, \ \ \ \{(i,i) | i\in\{1\cdots n\}\} \subset S\),

A decomposition of the form \(A=LU-R\) where the following hold

  • \(L\in \mathbb {R}^{n\times n}\)  is a lower unitriangular matrix
  • \(U\in \mathbb {R} ^{n\times n}\) is an upper triangular matrix
  • \(\displaystyle L,U\) are zero outside of the sparsity pattern i.e. \(L_{ij}=U_{ij}=0\quad \forall \;(i,j)\notin S\)
  • \(R\in \mathbb {R} ^{n\times n}\) is zero within the sparsity pattern i.e.\(R_{ij}=0\quad \forall \;(i,j)\in S\)

Preconditioners

Incomplete Cholesky factorization

A sparse approximation of the Cholesky factorization.

Recall the Cholesky factorization of a positive definite matrix \(A\) is \(A\) = \(LL^*\) where \(L\) is a lower triangular matrix. 

Incomplete Cholesky factorization is a sparse approximation to \(L\) lower triangular matrix \(M\) that is close to \(L\). The corresponding preconditioner is \(MM^*\).

Use the algorithm for finding the exact Cholesky decomposition, except that any entry is set to zero if the corresponding entry in A is also zero.

Preconditioners

Incomplete Cholesky factorization

A sparse approximation of the Cholesky factorization. 

def ichol(A):
    n = A.shape[0]
    L = np.zeros(A.shape)
    for k in range(n):
        L[k,k] = sqrt(A[k,k])
        for i in range(k+1):
            if A[i,k] != 0:
                L[i,k] = A[i,k]/L[k,k]
    return L

Preconditioners

Symmetric SOR

If the original matrix can be split into diagonal, lower and upper triangular as \(A=D+L+L^T\) then the SSOR preconditioner matrix is defined as

\(M(\omega) = \frac{\omega}{2-\omega}\left(\frac{1}{\omega} D + L\right)D^{-1}\left(\frac{1}{\omega} D + L\right)^T\)

 

What makes a good preconditioner?

Multigrid

Many iterative methods have the smoothing property where oscillatory modes of the error are eliminated effectively, but smooth modes are damped slowly.

So we transform the problem such that we forcibly dampen lower frequency error modes. I.e we solve a similar problem on coarser grids, then use that as an estimate for our initial guess

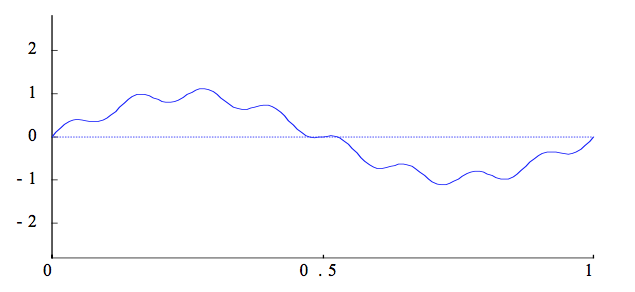
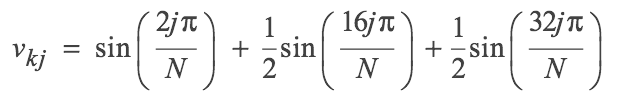
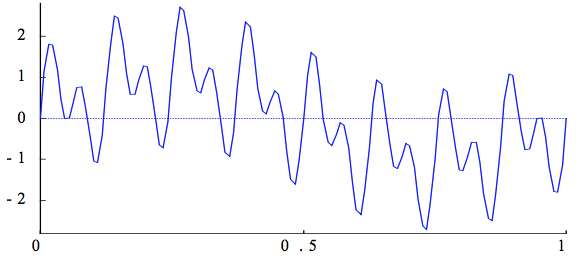
After a few iterations

Example Problem

One dimensional boundary value problem

-u^{\prime\prime}(x) + \sigma u(x) = f(x)

We want to find a function \(u(x)\) satisfying the above.

Model Problem

 For \(0 < x < 1\), \(\sigma > 0\) with \(u(0)=u(1)=0\)

Example Problem

One dimensional boundary value problem

-u^{\prime\prime}(x) + \sigma u(x) = f(x)

Grid:

\(h:=\frac{1}{N}, x_j = jh, j = 0,1, \cdots N\)

\(x_0, x_1, x_2\)

\(x_j\)

\(x_N\)

Let \(f_i = f(x_i)\) and \(v_i \approx u(x_i)\), we want to recover \(v_i\)

\(\cdots\)

\(\cdots\)

\(\cdots\)

\(x_0, x_1, x_2\)

\(x_j\)

\(x_{N/2}\)

\(\cdots\)

\(\cdots\)

\(\Omega_h\)

\(\Omega_{2h}\)

Residual Correction

If we call \(e = \tilde{x} - x \), that is, \(e\) is the error between an approximation and ground truth, then \(A(\tilde{x} + e) = b\)

It follows that \(Ae = r\), so solve for \(e\) approximately, then add that to \(\tilde{x}\).

Coarse grid correction

Given an approximation to \(x\), calculate the residual \(r\) then project onto a coarser grid (restriction).

Solve for \(e\) on coarser grid, with a coarser approximate operator to \(A\).

Interpolate \(e\) on the finer grid, and perform residual correction (prolongation).

Restriction

Given an approximation to \(x\), calculate the residual \(r\) then project onto a coarser grid (restriction).

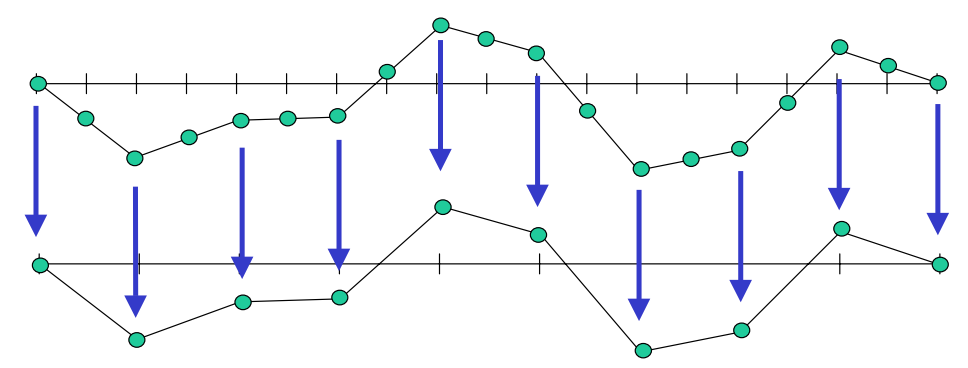
Prolongation

Interpolate \(e\) on the finer grid, and perform residual correction (prolongation).

Parallel Numerical Methods: Iterative Methods & Preconditioners

By Joshua Horacsek

Parallel Numerical Methods: Iterative Methods & Preconditioners

  • 636

More from Joshua Horacsek