最小编辑距离
最小编辑距离
给定两个字符串 a 和 b,只允许以下三种操作:
1. 插入一个字符;
2. 删除一个字符;
3. 替换一个字符。
求:把 a 转换成 b 的最小操作次数
假设,a 的长度是 m,b 的长度是 n,要求 a[1]a[2]...a[m] => b[1]b[2]...b[n] 的最小编辑距离,记为 d[m][n]。
解决方案一:递归
1. 如果 a[m] === b[n] => d[m][n] === d[m-1][n-1]
2. 如果 a[m] !== b[n]
2.1 d[m][n] === d[m-1][n] + 1
eg: (xyz -> efg) === (xy -> efg) + 1
2.2 d[m][n] === d[m][n-1] + 1
eg: (xyz -> efg) === (xyzg -> efg) + 1 === (xyz -> ef) + 1
2.3 d[m][n] === d[m-1][n-1] + 1
eg: (xyz -> efg) === (xyg -> efg) + 1 === (xy -> ef) + 1
3. m = 0 => (a -> b) === n n = 0 => (a -> b) === m
解决方案一:递归
function recursion(a, b, i, j) {
if (j === 0) {
return i;
} else if (i === 0) {
return j;
} else if (a[i - 1] === b [j - 1]) {
return recursion(a, b, i - 1, j - 1);
} else {
let m1 = recursion(a, b, i - 1, j) + 1;
let m2 = recursion(a, b, i, j - 1) + 1;
let m3 = recursion(a, b, i - 1, j - 1) + 1;
return Math.min(m1, m2, m3);
}
}解决方案二:动态规划
思路与递归相反
递归的逻辑是:
要求得 d[m][n],先要求得 d[m-1][n-1]……
动态规划的逻辑是:
先求得 d[m-1][n-1],再求 d[m][n]……
解决方案二:动态规划
已知 d[0][0],d[0][1],d[1][0],求 d[1][1]:
- 如果 a[1] === b[1],那么 d[1][1] 等于 d[0][0],也就是 0;
- 如果 a[1] !== b[1],那么 d[1][1] 等于 d[0][1]、d[1][0] 和 d[0][0] 三者中的最小值 + 1,也就是 1。
依次类推,求得d[1][2]、d[1][3]、……、d[1][n],然后求得d[2][1]、d[2][2]、……、d[2][n],最终求得d[m][n]
解决方案二:动态规划
举个例子:sdjfksdk => sdkfjkks
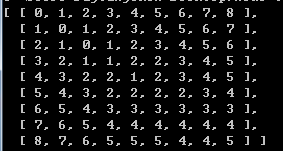
解决方案二:动态规划
function dynamicPlanning(a, b) {
let lenA = a.length;
let lenB = b.length;
let d = [];
d[0] = [];
for (let j = 0; j <= lenB; j++) {
d[0].push(j);
}
for (let i = 0; i <= lenA; i++) {
if (d[i]) {
d[i][0] = i;
} else {
d[i] = [];
d[i][0] = i;
}
}
for (let i = 1; i <= lenA; i++) {
for (let j = 1; j <= lenB; j++) {
if (a[i - 1] === b[j - 1]) {
d[i][j] = d[i - 1][j - 1];
} else {
let m1 = d[i - 1][j] + 1;
let m2 = d[i][j - 1] + 1;
let m3 = d[i - 1][j - 1] + 1;
d[i][j] = Math.min(m1, m2, m3);
}
}
}
return d[lenA][lenB];
}方案对比
1. 空间复杂度
递归: O(n)
动态规划: O(n ^ 2)
2. 时间复杂度
递归: O(m ^ n)
动态规划: O(m * n)
动态规划在空间上的优化
用一维数组来表示?
动态规划在空间上的优化
function dynamicPlanning(a, b) {
let lenA = a.length;
let lenB = b.length;
let d = [];
let i, j, old, tnmp;
for (j = 0; j <= lenB; j++) {
d[j] = j;
}
for (i = 1; i <= lenA; i++) {
old = i - 1;
d[0] = i;
for (j = 1; j <= lenB; j++) {
temp = d[j];
if (a[i-1] == b[j-1]) {
d[j] = old;
} else {
d[j] = min(d[j] + 1, d[j-1] + 1, old + 1);
}
old = temp;
}
}
return d[lenB];
}
function min(...inputs){
return inputs.reduce((pre, cur) => pre > cur ? cur : pre);
}动态规划在空间上的优化
优化之后:
空间复杂度:O(min(m,n))
无法回溯
Thank you
最小编辑距离与动态规划
By Joson Chen
最小编辑距离与动态规划
- 723



