關於二分圖匹配
建國中學 賴昭勳
圖論上的匹配
還有其他類似的東西
名詞定義
- 匹配(Matching): 一個無向圖\(G = (V, E)\)的匹配\(M\)是一個邊集,使得\(M \subseteq E\) 且\(M\)裡面任兩條邊都沒有共用點。
- 匹配邊: 被選在目前匹配裡的邊。
- 匹配點: 某個匹配邊的端點。
- 極大匹配(Maximal Matching): 一個匹配\(M\)不存在匹配\(M'\)使得\(M \subset M'\)時稱為極大匹配。
- 最大匹配(Maximum Matching): 所有匹配中配對邊數最多者。
- 完美匹配(Perfect Matching): 所有點都是匹配點的匹配
Maximal v.s. Maximum
- 點(邊)覆蓋 (Vertex/Edge cover): 圖上的一個點(邊)集使得所有邊(點)都和該集合的點(邊)相鄰。
- (點)獨立集(Independent Set):圖上的一個點集\(I\)使得\(I\)內任兩個點不相鄰。 (邊獨立集就是指匹配)
Vertex Cover Independent Set
最大/最小
匹配/點覆蓋/獨立集?
在一般圖上:
- 最大匹配: P 問題
- 最小點覆蓋: NP-Hard
- 最小邊覆蓋: P 問題
- 最大獨立集: NP-Hard
重要的性質
\(|最大匹配| + |最小邊覆蓋| = |最小點覆蓋| + |最大獨立集| = |V|\)
而且在二分圖上 |最大匹配| = |最小點覆蓋|
在二分圖上,求出最大匹配的演算法很好寫,也蠻常出現在題目中,所以十分重要。
二分圖匹配演算法
Bipartite Matching Algorithms
交替/增廣路徑
交替路徑 (Alternating Path):
從一個點開始,依序交替經過匹配邊和未匹配邊的路徑
增廣路徑 (Augmenting Path):
起點和終點都是未匹配點的交替路徑
增廣路徑->增加匹配大小
出現增廣路徑時,可以將匹配邊和未匹配邊交換,匹配的大小會增加一。
Berge's lemma
一個匹配是最大匹配 若且唯若 不存在增廣路徑。
兩個方向都要證明
一、最大匹配沒有增廣路徑 -> 有增廣路徑就不是最大匹配。顯然正確。
二、沒有增廣路徑就代表是最大匹配:
假設目前的匹配是\(M\)有一個更大的匹配\(M'\)。則考慮兩者的對稱差\(G' = (M \backslash M') \cup (M' \backslash M)\)
可以知道\(G'\)的每個點度數\(\leq 2\),且如果\(deg=2\)的話一定是連到一條\(M\)和一條\(M'\)的邊。因此\(G'\)會由孤點、交錯偶環和交錯路徑構成。因為\(|M'| > |M|\),多的那些邊一定是出現在交錯路徑上,也就代表增廣路徑存在。Q.E.D.
因此我們得到一個演算法:
維護當前的匹配\(M\),直到沒有增廣路徑為止。
另外可以注意到,在對增廣路徑「換邊」的時候,原本的匹配點仍然是匹配點,而起終點兩個未匹配點會變成匹配點。
而且,在二分圖上如果存在增廣路徑的話,起終點一定在二分圖的兩邊。
二分圖匹配演算法
枚舉其中一側的所有點,從該點開始找增廣路徑,找到的話就換邊。
根據前面的兩個性質,我們可以保證這樣就一定找得到最大匹配。
那要怎麼找增廣路徑?
簡單的DFS就可以了!
找增廣路徑
接下來我們以左/右邊代表二分圖的兩側。
從左邊開始走的時候,第一條是未匹配邊走到右邊,如果右邊這個點是未匹配點就找到增廣路徑了,否則他要走匹配邊,只有一個選擇走回左邊...
這個叫做
「交替路徑樹」
很重要,之後會用到。
直接看實作吧
//Challenge: Accepted
//模板已省略
int n, m;
int mx[maxn], my[maxn];
bool adj[maxn][maxn], vis[maxn];
bool dfs(int n) {
if (vis[n]) return false;
vis[n] = 1;
for (int v = 1;v <= n;v++) {
if (!adj[n][v]) continue;
if (!my[v] || (my[v] && dfs(my[v]))) {
mx[n] = v, my[v] = n;
return true;
}
}
return false;
}
int main() {
// 輸入圖
int cnt = 0;
for (int i = 1;i <= n;i++) {
for (int j = 1;j <= n;j++) vis[j] = 0;
if (dfs(i)) {
cnt++;
}
}
cout << cnt << endl;
}時間複雜度: \(O(VE)\)
常數超級小,算出來是\(10^9\)也會過
跟Dinic 類似的優化: Hopcroft-Karp Algorithm ,複雜度\(O(E \sqrt V)\)
二分圖最小點覆蓋
Minimum Vertex Cover
證明方式: 構造法
Step 1:
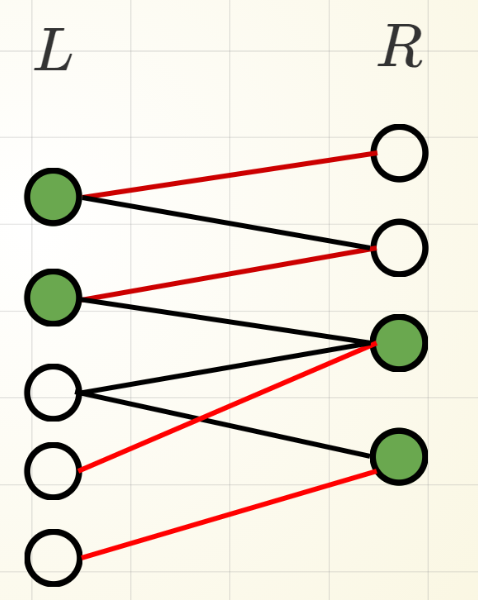
令 \(U = \{L 上沒有匹配的點\}\)
紅邊: 匹配邊
黑邊: 未匹配邊
證明方式: 構造法
Step 2:
從\(U\)的點開始DFS,規定只能走交替路徑。把所有經過的這些點集合稱為 \(T_L\) (左半) 和\(T_R\) (右半)
注意到這個交替路徑長相一定是:
\(U\)->黑邊->R->紅邊->L ...
證明方式: 構造法
Step 3:
點覆蓋為
\((L \backslash T_L) \cup (R \cap T_R)\)
用交錯路徑樹的觀點
上面的論述等同於: 用\(L\)的未匹配點找交錯路徑森林,則最小點覆蓋為\(L\)不在樹上的點和\(R\)在樹上的點。
可以試著從這個方向感受一下為什麼這是正確的。
正確性證明:
1. 這真的是點覆蓋
2. 這是最小點覆蓋->大小和最大匹配相同
正確性證明
1. 這真的是點覆蓋:
不存在邊\((x, y)\)使得 \(x \in T_L,y \in (R \backslash T_R)\)
假設\(x \in T_L\)
如果該邊是紅邊,\(x\)就是從\(U\)開始經過這條邊找到交替路徑,故\(y \in T_R\),矛盾。
如果是黑邊,交替路徑就一定可以走到\(y\),\(y \in T_R\) 依舊成立。
正確性證明 pt.2
2. 這是最小點覆蓋->大小和最大匹配相同
首先,\(|最小點覆蓋| \geq |最大匹配|\),因為最大匹配的每一條邊都要被一個不一樣的點覆蓋住。
因此我們只要能夠證明每個點都會連接到一條不同的匹配邊,那根據 1.,這會是一個大小為最小可能值,也就是\(|最大匹配|\)的點覆蓋。
每個在\(L \backslash T_L\)的點都有匹配,因為
每個在\(T_R\)的點都有匹配,否則從\(U\)走到\(T_R\)的路徑就會形成增廣路徑,矛盾。
而且,因為\(T_R\)匹配到的邊在\(T_L\)裡,兩者不重複。 \(Q.E.D.\)

Code:
//Challenge: Accepted
//模板已省略
int n, m;
int mx[maxn], my[maxn];
bool adj[maxn][maxn], vis[maxn], cx[maxn], cy[maxn];
bool dfs(int n) {
if (vis[n]) return false;
vis[n] = 1;
for (int v = 1;v <= m;v++) {
if (!adj[n][v]) continue;
if (!my[v] || (my[v] && dfs(my[v]))) {
mx[n] = v, my[v] = n;
return true;
}
}
return false;
}
void dfs2(int n) {
if (vis[n]) return;
vis[n] = 1;
cx[n] = 0;
for (int v = 1;v <= m;v++) {
if (!adj[n][v]) continue;
cy[v] = 1;
if (my[v]) {
dfs2(my[v]);
}
}
}
int main() {
// 輸入圖
int cnt = 0;
vector<int> u;
for (int i = 1;i <= n;i++) {
for (int j = 1;j <= n;j++) vis[j] = 0;
if (dfs(i)) {
cnt++;
} else {
u.push_back(i);
}
}
for (int i = 1;i <= n;i++) {
cx[i] = 1, vis[i] = 0;
}
for (int i:u) dfs2(i);
cout << cnt << "\n";
for (int i = 1;i <= n;i++) {
if (cx[i]) cout << i << " ";
}
for (int i = 1;i <= m;i++) {
if (cy[i]) cout << n + i << " ";
}
cout << endl;
}
Problems I
重點: 活用匹配「任兩條邊端點不重複」的特性,找到好的建圖方式解決問題。
有時候用最小點覆蓋想,再把它轉換到最大匹配。
給一個 n \text{ x } n, n \leq 10^3\(n*n\)的01矩陣
每次操作可交換任兩行,或任兩列
請輸出一組操作使的主對角線上面都是 1
最多做 nn 次操作。
無解輸出 -1
\(n \leq 1000\)
在一個\(n*n\)的棋盤上面有一些怪物,每次可以選擇一直行或一橫列消除所有的怪物,請找出消除所有怪物的最少操作數。
\(n \leq 1000, 怪物個數 \leq 20000\)
給一個 \(n*m\)的01表格,每次操作能任意交換兩行或兩列,求任意次數交換過後全部由 1 組成的最大子矩形周長。
一開始表格的四周都是 1 。
\(n, m \leq 200\)
給你\(n\)個相異的正整數,請找出最少須移除幾個數字才能讓剩下的集合內任兩個數字的和不是質數。輸出你要移除的數字。
\(n \leq 2000, a_i \leq 10^5\)
在二維平面上有\(m\)個緊急事件,第\(i\)個位於\((x_i, y_i)\),並會在時間\(t_i\)發生。你需要指派警察去處理事件。一個警察一開始可以出現在任意位置,之後每單位時間能朝上下左右移動一格(或不動)。警察必須要在事件發生時位於事件的位置,問最少需要幾個警察才能處理所有事件。
\(m \leq 1000, x_i, y_i \leq 1000, t_i \leq 1440\)
你有一個\(d\)個按鈕的密碼鎖,每個按鈕可以是開(1)或關(0)兩種狀態。一開始所有按鈕都是0。
每次操作可以:
- 將某個0的按鈕變成1
- 將所有按鈕重設為0
有\(n\)種可能的密碼組合,請輸出一組最短的操作順序,使得這\(n\)種組合都會在操作的過程中出現。
\(d \leq 10, n \leq 2^d - 1\)
二分圖最大/最小權匹配
KM演算法/匈牙利演算法
問題簡介
給定一個兩邊各\(n\)個節點的完全二分圖,每條邊都有權重\(c(u, v)\),找到一個權重最大的完美匹配(每個點都有匹配)。
另一個形式是: 給你一個\(n*n\)的方陣,每個格子裡有一個數字。選擇一些格子使得每排、每列都只選到一個,並最大化權重。
問題簡介
註: 若要求最小權重的答案,可以將所有邊權變號\(c(u, v) := -c(u, v)\),最後再把答案變號即為所求。
| 7 | 5 | 3 | 10 | |
| 2 | 5 | 7 | 6 | |
| 10 | 1 | 4 | 9 | |
| 11 | 8 | 1 | 9 |
轉換問題
給每個節點一個點權\(l(v)\) (vertex labeling),使得對於每一條邊\((u, v)\)都有\(l(u) + l(v) \geq c(u, v)\)。
恰好符合\(l(u) + l(v) = c(u, v)\)的邊稱為緊邊。
對於一張二分圖\(G\),我們把只有緊邊的圖稱為緊邊子圖\(G'\)。
| 3 | 2 | 0 | 7 | |
|---|---|---|---|---|
| 3 | 1 | 0 | 0 | 0 |
| -1 | 0 | 4 | 8 | 0 |
| -1 | 8 | 0 | 5 | 3 |
| 1 | 7 | 5 | 0 | 1 |
如果\(G'\)有完美匹配,那該匹配為最佳解,權重為所有點的和\(\sum l(v)\)
定義一條邊\((u, v)\)的相對邊權為 \(l(u) + l(v) - c(u, v)\)
演算法過程
- 一開始先隨意找一個合法的 vertex labeling,常見方式是將一邊的點權設為他連到的邊權最大值,另一邊設為\(0\)。
- 當緊邊子圖的匹配大小\(< n\)的時候做兩件事:
- 增加匹配大小
- 改變點權使其他緊邊出現。
注意到,我們限制匹配到的邊一定要是緊邊。
增加匹配大小就用dfs在\(G'\)找增廣路徑就好了。
第二點要怎麼做到?
演算法過程
假設我們現在找到\(G'\)的最大匹配,並用König's Theorem 的方法找到了最小點覆蓋。
因為目前還不是完美匹配,一定存在非緊邊(藍)\((u, v)\)使得
\(u \in T_L, v \in R \backslash T_R\)
令\(\Delta\)為這些藍邊的相對邊權最小值,那讓\(T_L\) 的點權重扣掉\(\Delta\),讓\(T_R\)的點權重加上\(\Delta\)
演算法過程
改完點權之後,每個邊的相對邊權發生了什麼事?
- 藍邊的權重扣掉\(\Delta\)
- 連了一個綠點的邊不變 (所有的匹配邊都是這種)
- 連了兩個綠點的邊增加\(\Delta\)
注意到,因為\(\Delta\)的定義,至少有一條藍邊會變成緊邊,也就代表說\(T\)的大小至少增加一,並且到最後一定有增廣路徑出現。
實作細節/另一個角度
實際上在寫匈牙利演算法時會用稍微不一樣的方法實作,但是背後的原理是一樣的。
就跟最大匹配的方式一樣,從一邊的點開始枚舉。如果找到增廣路徑就直接匹配。
否則從該點建緊邊的交錯路徑樹,找連出去的非緊邊,取相對邊權的最小值,再用前面的方法改值。
可以直觀的看出,交錯路徑樹至少多一個點,並且因為這個根節點一定配得到東西,總有一天會找到增廣路徑。
實作細節/另一個角度
可以把它當成是對前\(i\)個點找到答案,每次新增一個未匹配點之後,\(T\)就是那個點的交錯路徑樹。
時間複雜度?
對於\(n\)個點,每次dfs要\(O(n^2)\),交錯路徑樹每次多至少一個點,總共可能增加\(O(n)\)次,
故複雜度為\(O(n^4)\)
Code:
//Challenge: Accepted
//模板已省略
int a[maxn][maxn];
int lx[maxn], ly[maxn], mx[maxn], my[maxn];
bool vx[maxn], vy[maxn];
int tot;
bool dfs(int n) {
if (vx[n]) return false;
vx[n] = 1;
for (int v = 1;v <= tot;v++) {
if (lx[n] + ly[v] - a[n][v] > 0) continue;
//only check tight edges
vy[v] = 1;
if (!my[v] || dfs(my[v])) {
mx[n] = v, my[v] = n;
return true;
}
}
return false;
}
int main() {
io
int n;
cin >> n;
tot = n;
for (int i = 1;i <= n;i++) { //input
for (int j = 1;j <= n;j++) {
cin >> a[i][j];
}
}
for (int i = 1;i <= n;i++) { //initialize vertex labeling
lx[i] = 0;
for (int j = 1;j <= n;j++) lx[i] = max(lx[i], a[i][j]);
}
for (int i = 1;i <= n;i++) {
while (true) {
for (int j = 1;j <= n;j++) vx[j] = vy[j] = 0;
if (dfs(i)) {
break;
}
int delta = 1<<30;
for (int j = 1;j <= n;j++) {
if (!vx[j]) continue;
for (int k = 1;k <= n;k++) {
if (!vy[k]) {
delta = min(delta, lx[j] + ly[k] - a[j][k]);
}
}
}
for (int j = 1;j <= n;j++) {
if (vx[j]) lx[j] -= delta;
if (vy[j]) ly[j] += delta;
}
}
}
int ans = 0;
for (int i = 1;i <= n;i++) ans += lx[i] + ly[i];
cout << ans << "\n";
for (int i = 1;i <= n;i++) cout << lx[i] << " ";
cout << "\n";
for (int i = 1;i <= n;i++) cout << ly[i] << " ";
cout << "\n";
} 還沒完呢!
可以優化到\(O(n^3)\)
目前的複雜度瓶頸有兩個。
- DFS每次\(O(n^2)\)要做\(n^2\)次
- 每次找到最小邊的時間是\(O(n^2)\),雖然調點權只需要\(O(n)\)。
優化到\(O(n^3)\)
維護一個陣列 \(slack[i]\),代表右邊每個點與交錯路徑樹之間的相對邊權最小值。
\(slack[i] = min_{x \in T_x}(l(x) + l(i) - c(x, i))\)
當\(slack[i] = 0\)時,該點有(至少)一條連到樹上的邊,因此他會被加入到樹中。
因此,在非樹點和樹點之間的最小邊權可以透過從\(slack\)裡面找非樹點的最小值得到。
改變點權時,非樹點的\(slack\)會扣掉\(\Delta\),樹點則不變。
那DFS怎麼辦?
我們只要找到一個增廣路徑就可以break 了。
在還沒找到之前,會一直把新的點加進交錯路徑樹,而這棵樹前面的結構也不會改變。所以,我們可以只從新的點開始DFS,直到找到交錯路徑!
實作上在維護\(vis\)的時候不要重設,每次從非樹點裡面\(slack = 0\)的開始DFS,對每個點來說都只會跑整張圖一次,複雜度是均攤\(O(n^2)\)。
再加上前面的優化,就成功達成\(O(n^3)\)了!
My Code, And 蛋餅的寫法
//Challenge: Accepted
//模板已省略
int a[maxn][maxn];
int lx[maxn], ly[maxn], mx[maxn], my[maxn];
bool vx[maxn], vy[maxn], check[maxn];
int slack[maxn];
int tot;
bool dfs(int n, bool ch) { //ch is true if we want to change matching
if (vx[n]) return false;
vx[n] = 1;
for (int v = 1;v <= tot;v++) {
//n is in the tree, so we should update slack[v] here
slack[v] = min(slack[v], lx[n] + ly[v] - a[n][v]);
if (lx[n] + ly[v] - a[n][v] > 0) continue;
vy[v] = 1;
if (!my[v] || dfs(my[v], ch)) {
if (ch) mx[n] = v, my[v] = n;
return true;
}
}
return false;
}
int main() {
io
int n;
cin >> n;
tot = n;
for (int i = 1;i <= n;i++) { //input
for (int j = 1;j <= n;j++) {
cin >> a[i][j];
}
}
for (int i = 1;i <= n;i++) { //init vertex labeling
for (int j = 1;j <= n;j++) lx[i] = max(lx[i], a[i][j]);
}
for (int i = 1;i <= n;i++) {
for (int j = 1;j <= n;j++) vx[j] = vy[j] = check[j] = 0;
for (int j = 1;j <= n;j++) slack[j] = 1<<30; //init slack
check[i] = 1;
//check[i] is 1 if vertex i is in the tree and
//should be searched the next time
bool aug = 0;
while (!aug) {
for (int j = 1;j <= n;j++) {
if (check[j] && dfs(j, 0)) {
aug = 1;
break;
}
}
if (aug) break;
int delta = 1<<30;
for (int j = 1;j <= n;j++) {
if (!vy[j]) delta = min(delta, slack[j]);
check[j] = 0;
}
for (int j = 1;j <= n;j++) {
if (vx[j]) lx[j] -= delta;
if (vy[j]) ly[j] += delta;
else {
slack[j] -= delta;
if (slack[j] == 0) {
vy[j] = 1;
//vertex j is now added to the tree
if (!my[j]) {
aug = 1;
} else {
check[my[j]] = 1;
}
}
}
}
}
for (int j = 1;j <= n;j++) vx[j] = vy[j] = 0;
dfs(i, 1); //actually change the matching
}
int ans = 0;
for (int i = 1;i <= n;i++) ans += lx[i] + ly[i];
cout << ans << "\n";
for (int i = 1;i <= n;i++) cout << lx[i] << " ";
cout << "\n";
for (int i = 1;i <= n;i++) cout << ly[i] << " ";
cout << "\n";
} Problems II
基本上就是裸的KM w
帶權+要輸出解的砲打皮皮
給你兩個\(r*c\)的表格\(A, B\),每個格子是紅色或綠色,每次操作可以選擇花\(F\)元改變任意一格的顏色,或花\(S\)元交換相鄰兩格的顏色。求把\(A\)變成跟\(B\)一樣的最少花費。
\(r, c \leq 10, 1 \leq F, S \leq 10^6\)
Subtask 1: \(F, S = 1\)
額外資源
關於二分圖匹配 (資讀)
By justinlai2003
關於二分圖匹配 (資讀)
- 1,649



