高斯消去+一般圖匹配
矩陣乘法?
行列式?
行列式(det)
\(det(A) = \sum\limits_{\sigma \in S_{n}}\operatorname {sgn}(\sigma )\prod\limits_{i=1}^{n}A_{i,\sigma (i)}\)
其中\(\operatorname{sgn}( \sigma) = (-1)^{N(\sigma)}\)
\(N(\sigma)\)是逆序數對數或將該排列排好所需的對換數
(兩者奇偶性相同)
降階
高斯消去
示範
*把一行乘k加到另一行行列式值不變
code
void Gauss(double A[509][509],ll N)
{
ll i,j,k,r;
for(i = 0;i < N;i++)
{
r = i;
for(j = i+1;j < N;j++) if(abs(A[j][i]) > abs(A[r][i])) r = j;
if(r != i)
{
for(j = 0;j < N;j++)
{
swap(A[r][j],A[i][j]);
}
}
for(k = i+1;k < N;k++)
{
double f = A[k][i]/A[i][i];
for(j = i;j < N;j++) A[k][j] -= f*A[i][j];
}
}
}複雜度?
用處
1.求行列式
- \(det(A) \neq 0 \Leftrightarrow A 可逆 \)
2.解(多元)一次方程組
3. 求秩(rank)
- 行秩 = 列秩
- \(rank(A) = n \Leftrightarrow det(A) \neq 0 \)
4.求反矩陣
一般圖匹配
縮花><
我不會QQ
可以用線性代數?!
Tutte Matrix
$$T(G)_{i,j} = \left\{\begin{matrix} 0 & if(v_i,v_j)\notin E(G)\\ x_{i,j} & if(v_i,v_j)\in E(G) \textrm{ and }i<j\\ -x_{i,j} & if(v_i,v_j)\in E(G) \textrm{ and }i>j\end{matrix}\right.$$
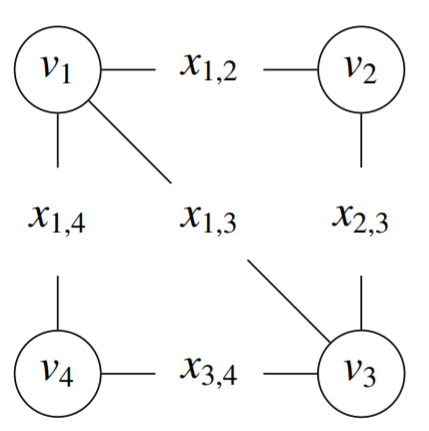
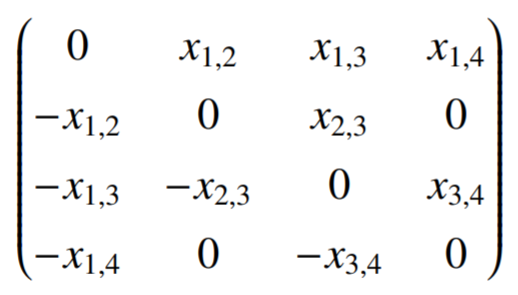
完美匹配
Tutte 定理(1947)
\(G\)有完美匹配\(\Leftrightarrow det(T(G)) = 0 \)
Try Try see.
證明
環覆蓋
用一堆有向環去覆蓋一個無向圖,使得每個頂點恰在一個環中。
可以用一個排列\(p\)表示,其中\(i \neq p_i\),且\((i,p_i) \in E(G)\)
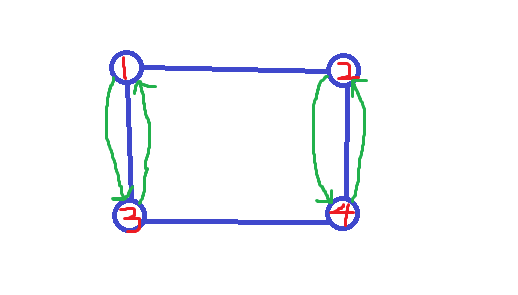
3 4 1 2
證明
\(det(T) = \sum\limits_{\sigma \in S_{n}}\operatorname {sgn}(\sigma )\prod _{i=1}^{n}T_{i,\sigma (i)}\)
考慮非零項
有機?
無機?
\(det(T(G)) \neq 0\)\(\Leftrightarrow G有完美匹配 \)
奇環覆蓋不會對det有貢獻
\(G\)有完美匹配\(\Leftrightarrow G有無奇環覆蓋 \)
複雜度?
不知道,但指數以上
Schwartz–Zippel lemma(之類的)
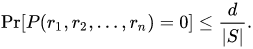
若\(P\)是一個有\(n\)個變數、最大度數為\(d\)的多項式,若從集合\(S\)中隨機取\((r_1,r_2,\cdots,r_n)\),則
\(O(N^3)\)
求出來
等等會用到的定義
\(A^{(S_1,S_2)}代表刪掉S_1中的行和S_2中的列所得到的新矩陣\)
\(A_{(S_1,S_2)}代表留下S_1中的行和S_2中的列所得到的新矩陣\)
斜對稱矩陣
\(一矩陣S,若-S = S^T,則稱S為斜對稱矩陣\)
Tutte Matrix就是
\(T^{-1}_{i,j} \neq 0 \Leftrightarrow G - (v_i,v_j) 有完美匹配 \)
\(A^{-1} = adj(A)/det(A) \)
\((adj(A))_{i,j} = (-1)^{i+j}det(A^{j,i}) \)
A:任意可逆矩陣
S : 斜對稱矩陣
T: Tutte Matrix
\(det(S^{i,j}) \neq 0\Leftrightarrow det(S^{(i,j),(i,j)}) \neq 0 (S可逆)\)
\(rank(S) 是偶數\)
\(S是 n \times n 且 n是奇數\Rightarrow det(S) = 0\)
\(可以找到S'=S_{(i_1,i_2...),(i_1,i_2...)},使det(S') \neq 0且 rank(S') = rank(S)\)
\(O(N^4)\)
每次只是刪兩行兩列,一定要重算反矩陣嗎?
若\(A = \begin{bmatrix} a& v^T \\ u & B \end{bmatrix},A^{-1} = \begin{bmatrix} \hat {a}& \hat v^T \\ \hat u & \hat B \end{bmatrix}\)
\(B^{-1} = \hat{B} - \hat{u}\hat{v}^T/\hat {a}\)
Finally
\(O(N^3)\)
感覺頗沒用?
最大匹配
Generalized Tutte Theorem
一張圖最大匹配的大小是\(rank(T(G))/2\)
\(可以找到S'=S_{(i_1,i_2...),(i_1,i_2...)},使det(S') \neq 0且 rank(S') = rank(S)\)
找出來
轉換
加/刪點找完美匹配
重點整理
剛剛都沒聽也沒怎樣
1.Tutte Matrix的定義
2.模一個大質數
3.隨機賦值
4.最大匹配大小是\(rank(T(G))/2\)
5.找最大匹配先轉完美匹配
6.\((i,j)可在完美匹配中\Leftrightarrow T^{-1}_{i,j} \neq 0\)
7.在原矩陣刪掉一行一列的話就用原逆矩陣對應的那行,消掉對應的那列,即可求出新的逆矩陣
例題
Undirected Vertex Geography
兩人玩遊戲,每次將棋子從圖上的一個節點移到相鄰且未走過的節點上,不可走者輸。哪些節點先手必勝?
結論
參考資料
deck
By Zi-Hong Xiao
deck
- 1,002



