圖論之匹配
匹配的定義
給定圖 \(G = (V, E)\)
一個匹配 \(M\) 為 \(G\) 的一個子圖,使的其中的邊,兩兩不相交
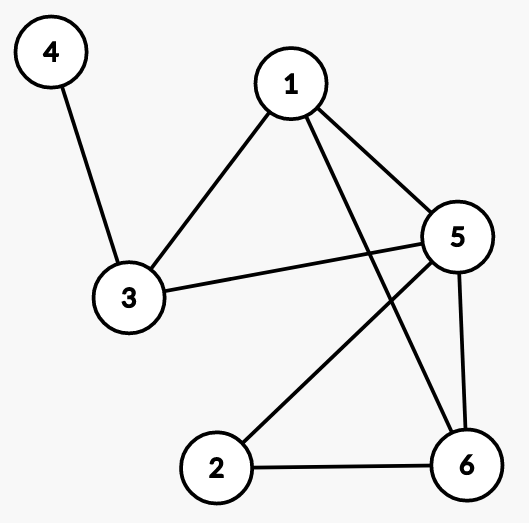
一些名詞
未匹配點
未匹配邊
交替路徑
增廣路徑
交替路徑

增廣路徑

極大匹配
一個匹配 \(M\) 使得無法被加入任何新的匹配
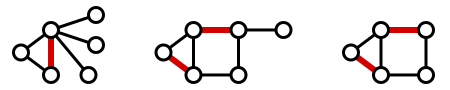
最大匹配
所有匹配中,包含最多匹配邊的那個

二分圖最大匹配
匈牙利演算法
對稱差集
集合 \(A, B\) 的對稱差集
\(A \oplus B = A \cap B - A \cup B\)
兩個匹配的對稱差集
\(M \oplus M^* = P\)
- 孤點
- 交替路徑
- 交替環
兩個匹配的轉換
\(M\oplus P = M^*\)
\(M^*\oplus P = M\)
Berge's lemma
在圖 \(G = (V, E)\) 上,
一個匹配 \(M\)為最大匹配
若且唯若找不到增廣路徑
尋找增廣路
紀錄每個點的匹配點
從未匹配點開始 DFS
沿著交錯路徑走
找到新的未匹配點就找到了增廣路
實做
const int maxn = 500;
vector<int> edge[maxn];
int ma[maxn], T, vis[maxn], n, m;
// 1 ~ n : left, n+1 ~ m : right
bool dfs(int now) {
if (exchange(vis[now], T) == T) return false;
for (int u : edge[now])
if (!ma[u] || dfs(ma[u]))
return ma[u] = now, ma[now] = u;
return false;
}
int get_max_matching() {
int res = 0;
for (int i = 1;i <= n;++i)
res += (!ma[i] && (++T, dfs(i)));
return res;
}
一些優化
把找擴充路徑改成 BFS
複雜度變成 \(O(\sqrt{|V|}|E|)\)
複雜度
找擴充路徑 \(O(|E|))\)
整體複雜度 \(O(|V||E|)\)
其他相關的事情
\(|最大點獨立集| + |最小點覆蓋| \)\(= |最大邊獨立集| + |最小邊覆蓋| = |V|\)
- \(|最大點獨立集| = |V| - |M|\)
- \(|最大邊獨立集| = |M|\)
- \(|最小點覆蓋| = |M|\)
- \(|最小邊覆蓋| = |V| - |M|\)
- 最大點獨立集
- 最大邊獨立集
- 最小點覆蓋
- 最小邊覆蓋
習題
CS acadmy
Flipping Matrtix
給一個 \(n \text{ x } n, n \leq 10^3\) 的 01 矩陣
每次操作可交換任兩行,或任兩列
最多做 \(n\) 次操作,
如果有解
請輸出一組操作使的主對角線上面都是 1
TIOJ 1253
給 \(n \text{ x } n , (n \leq 1000)\)的棋盤
上面有一些怪物
每次操作可以選一個橫排,或直排,把上面的怪物打掉
問至少要幾次操作才能消除所有的怪物
TIOJ 1601
在 \(n \text{ x } m , (n, m \leq 200)\)的鏡子上
0 代表破裂, 1 代表完好
每次操作可以交換兩個橫排,或兩個直排
可以做無限次操作。
定義一個完美的鏡子為一個鏡子使的它內部都完好
求做完操作後,週長最長的完美子鏡子
***每面輸入的鏡子最外面一整圈皆無破損,即皆為1
TIOJ 1069
外送公司接到了 \(n, n \leq 10^3\) 筆訂單
第 \(i\) 筆為 \(x_i, y_i, t_i\) 代表在座標 \(x_i, y_i\) 上有人會在 \(t_i\) 的時候領取到食物(外送員必須在那裡等待)
已知在兩組座標移動的時間為他們的曼哈頓距離,外送員可帶無限多的食物,並且處理多個訂單
請問你至少要派多少外送員才能滿足所有訂單
(派出一個外送員時,他可以瞬間出現在你想要的地方)
一般圖匹配
縮花演算法
花
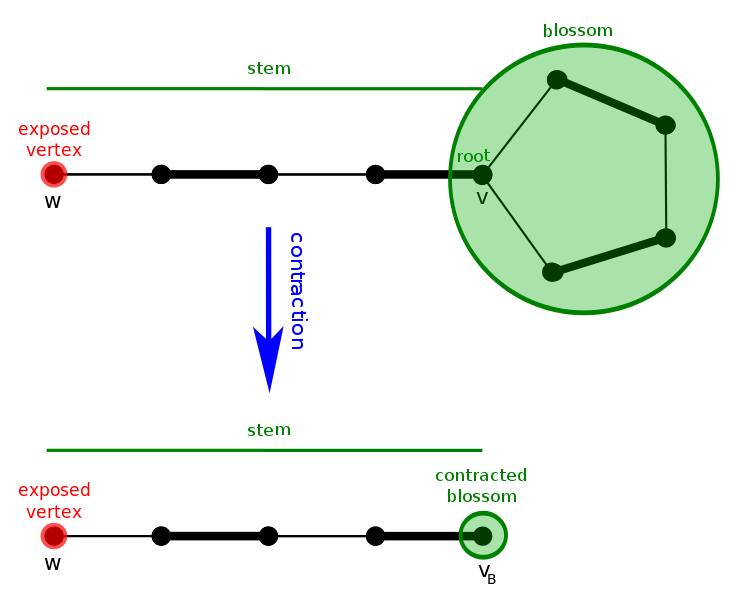
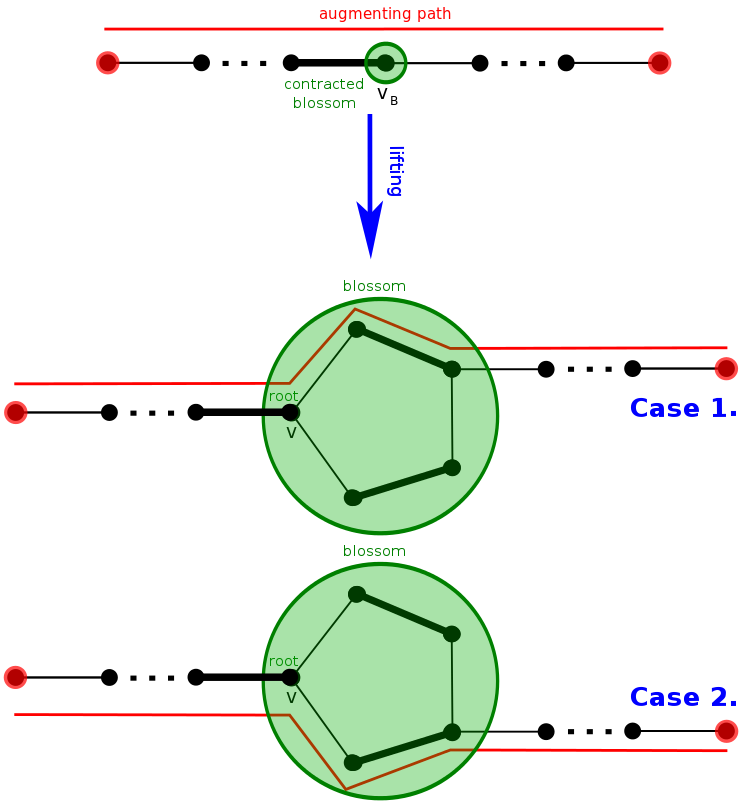
處理花的方法
- 用個 DSU 把他縮起來
(偏麻煩 - 直接處理好一些資訊,讓我們可以回朔出增廣路
(較好做
實做
int ma[maxn], lst[maxn], side[maxn], fid[maxn], n;
vector<int> edge[maxn];
void augment(int x, int y) {
while (x) {
int pa = ma[x];
ma[x] = y, ma[y] = x;
y = pa, x = lst[y];
}
}
實做
int find_lca(int x, int y) {
static int T, vis[maxn];
for (++T; ; swap(x, y)) {
if (x && exchange(vis[x], T) == T)
return x;
x = fid[lst[ma[x]]];
}
return -1;
}
bool bfs(int rt) {
#define qpush(x) (side[x] = 0, togo.push(x))
memset(side, -1, sizeof(side));
queue<int> togo;
qpush(rt);
auto flower = [&](int x, int y, int lca) {
while (x != lca) {
if (side[x] == 1) qpush(x);
lst[x] = y;
fid[x] = fid[y] = lca;
x = ma[x], y = lst[x];
}
};
while (!togo.empty()) {
int now = togo.front();
togo.pop();
for (int u : edge[now])
if (side[u] == -1) {
side[u] = 1;
lst[u] = now;
if (!ma[u])
return augment(now, u), true;
qpush(ma[u]);
}
else if (!side[u]) {
int lca = find_lca(u, now);
flower(u, now, lca);
flower(now, u, lca);
}
}
return false;
}
int max_matching() {
iota(fid, fid+n+1, 0);
int res = 0;
for (int i = 1;i <= n;++i)
res += !ma[i] && bfs(i);
return res;
}
實做參考來源:
日月掛長的 slides
圖論之匹配
By Kevin Zhang
圖論之匹配
- 1,255



