資料結構們
小複習
區間最大連續和
spoj GSS3
序列操作題
codeforces ???
- \(l, r, x, d\) : 把區間 \([l, r]\) 加上首項為 \(x\) 公差為 \(d\) 的序列
- \(l, r\) : 詢問區間和
矩形覆蓋面積計算
tioj 1224
二元搜尋樹
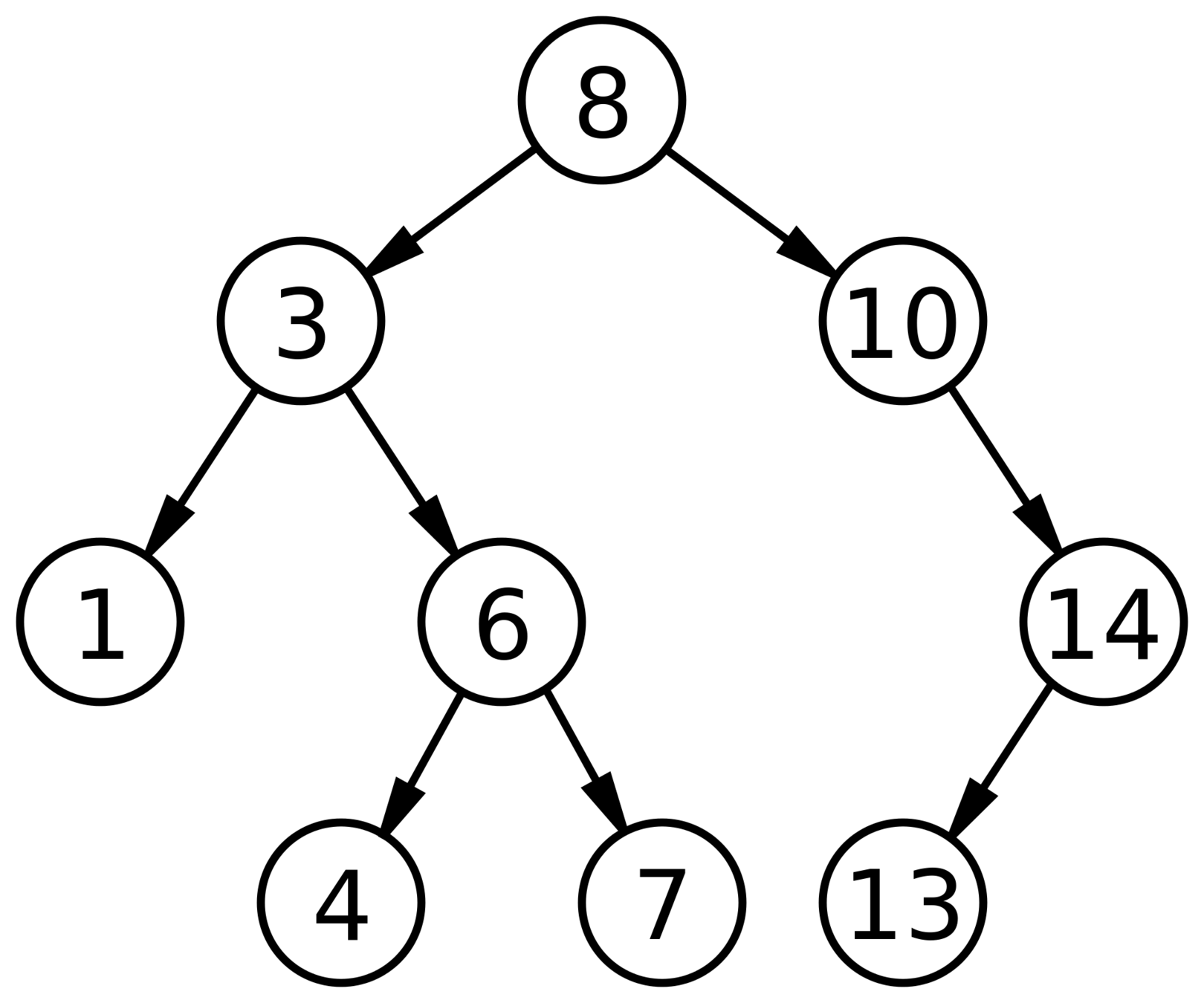
Naïve
binary search tree
- \(\mathcal{O}(n)\) insert \(x\) :
順著找到可以放的位置 -
\(\mathcal{O}(n)\) erase \(x\) :
找到它後拔掉 找到子樹中的 lower_bound( \(x\) ) ,然後把它換上來 -
\(\mathcal{O}(n)\) query \(x\):
在樹上(搞不好是鍊)二分(所以可能不算二分搜)搜
Tree + Heap = Treap
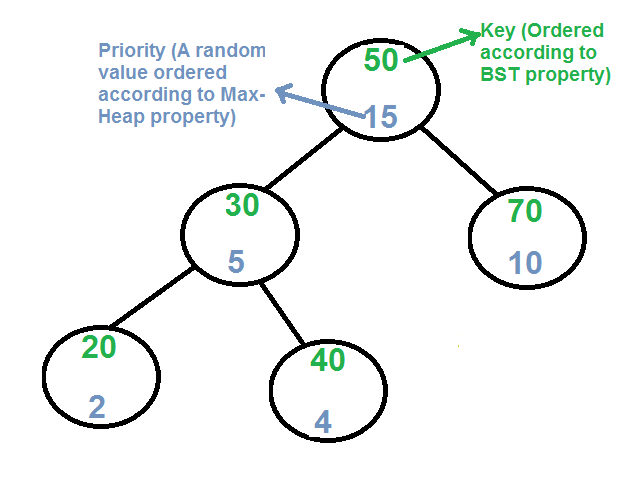
Treap
- \(\mathcal{O}(log_2 n)\) insert \(x\) :
???? -
\(\mathcal{O}(log_2 n)\) erase \(x\) :
???? - \(\mathcal{O}(log_2 n)\) query \(x\):
二分搜
Merge Split Treap
- Merge :
把一個 key 全部都小於等於 \(k\) 的 Treap
和一個 key 全部都大於等於 \(k\) 的 Treap
合併起來 - Split :
把一棵 Treap 分割成
一個 key 全部都小於 \(k\) 的 Treap 和
一個 key 全部都大於等於 \(k\) 的 Treap
- \(\mathcal{O}(log_2 n)\) insert \(x\) :
把自己 split 成 key < \(x\) 和 key \(\geq x\) 的兩塊 \(a, b\)
然後合併 \(a, x, b\) -
\(\mathcal{O}(log_2 n)\) erase \(x\) :
把自己 split 成 key < \(x\) 和 key \(\geq x\) 的兩塊 \(a, b\)
再把 \(b\) split 成 key \(\leq x\) 和 key > \(x\) 的兩塊 \(c, d\)
然後合併 \(a, c, d\) - \(\mathcal{O}(log_2 n)\) query \(x\):
二分搜
Merge Split Treap
Operation 1 : Merge
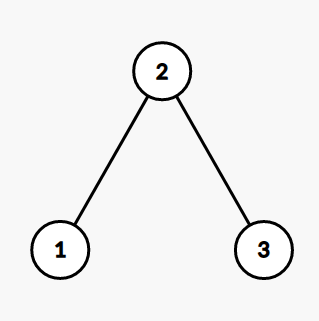
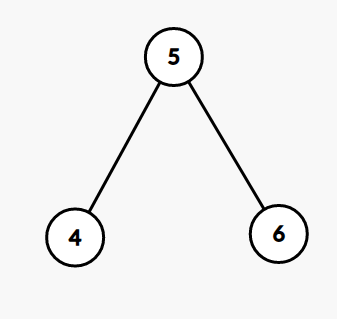
key \(\leq 3\)
key \(\geq 3\)


比較 pri
?


比較 pri

比較 pri


比較 pri


比較 pri

比較 pri


比較 pri


Operation 2 : Split
\(k = 4\)
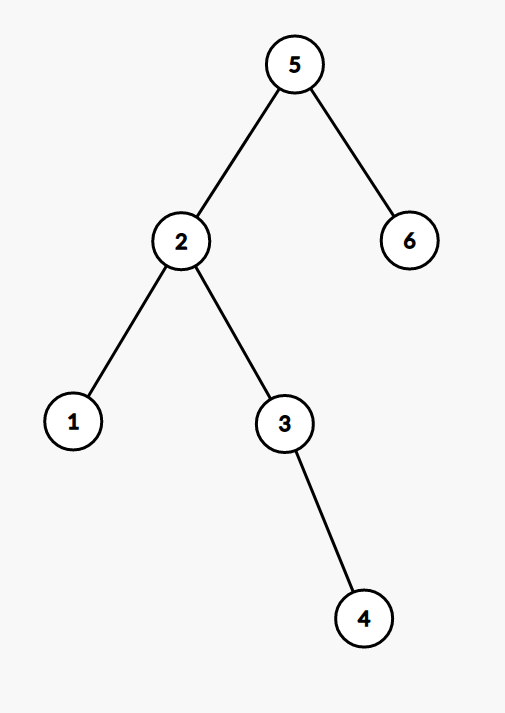
\(k = 4\)

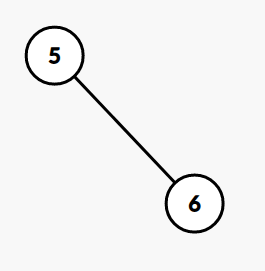
\(k = 4\)
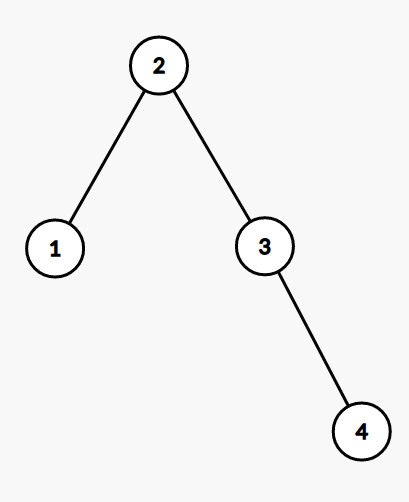
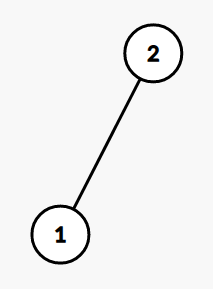
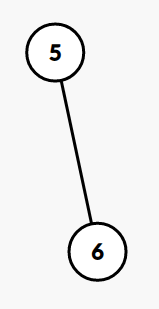
\(k = 4\)

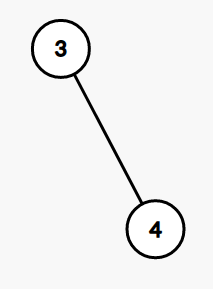

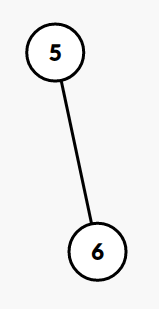
\(k = 4\)

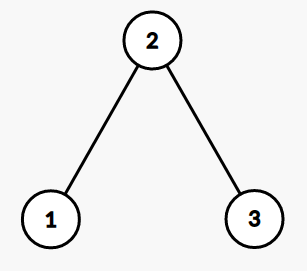

實做
unsigned ran() {
static unsigned x = 19;
return ++(x *= 0xdefaced);
}
struct node {
node * left = NULL, * right = NULL;
int key;
unsigned pri;
node(int key):key(key), pri(ran()){};
};
實做
node * merge (node* a, node* b) {
if (!a)return b;
if (!b)return a;
if (a->pri < b->pri) {
a->right = merge(a->right, b);
return a;
}
else {
b->left = merge(a, b->left);
return b;
}
}
實做
void split(node* now, int key, node* &a, node* &b) {
if (!now) {
a = b = NULL;
return;
}
if (now->key < key) {
a = now;
split(now->right, key, a->right, b);
}
else {
b = now;
split(now->left, key, a, b->left);
}
}
關於 treap 小技巧
- 其實 pri 值只有用在 merge 決定上下的時候
所以其實可以在那個時候 再決定就好
可以發現若兩棵樹的大小分別是 \(S_a, S_b\),那 麼 \(a\) 應該要在上層的機率約是 \(\frac{S_a}{S_a + S_b}\) - 如果順便維護子樹的大小,那就可以在樹上二分搜求出第 \(k\) 大的元素
- 在序列上,把 index 視為 key,則可以建出一個完整序列的 Treap,查詢區間時,只要把整格區間切下來並且維護子樹的資訊就好。可以做到線段樹支援的事情(只是比較慢....
TNFSHOJ 31
大榕樹的祈禱
維護一個序列,操作有以下
- \(\text{insert} p k v_1, v_2, v_3... v_k\):
把 \(k\) 個數字\(v_1, v_2, v_3...v_k\)插入在第 \(p\) 個數字的後面 - \(\text{delete} p k \):
從第 \(p\) 個數字開始連續刪除 \(k\) 個數字 - \(\text{make-same} p k v\) : 把 \(p\) 開始的連續 \(k\) 數字都改成 \(v\)
- \(\text{reverse} p k\) : 把 \(p\) 開始的連續 \(k\) 個數字倒轉
- \(\text{get-sum} p k\) : 計算從 \(p\) 開始的 \(k\) 個數字的和
- \(\text{max-sum}\) : 計算目前整個數列中最大的連續和
小例題
請維護一個集合,使得他支援兩種操作 :
- 加入一個數字 \(x\)
- 詢問目前第 \(k\) 大的數字
\(x \leq 10^5\)
操作數量 \(\leq 10^5\)
先假設線段樹不是代表一個序列,而是值域?
小例題
請維護一個集合,使得他支援兩種操作 :
ojdl 7129
- 加入一個數字 \(x\)
- 詢問目前第 \(k\) 大的數字
# : \(x \leq 10^9\)
操作數量 \(\leq 3 \cdot10^5\)
需要再開!
持久化
隕石
有一些城市 編號由 \(1 ~ n\)
有一些科學家想採集隕石樣本,而第 \(i\) 個城市需要採集 \(p_i\) 個
有 \(k\) 筆事件兩兩事件時間差為 1 且按照時間順序 \(l_i, r_i, a_i\) 表達在從 \([l_i, r_i]\) 都將會有 \(a_i\) 顆隕石墜落
請輸出 \(n\) 行代表在第 \(i\) 座城市至少要多久才能完成樣本採集
\(1 \leq n \leq 300000, 1 \leq k \leq 300000\)
如果我有 \(n\) 顆線段樹
第 \(i\) 顆線段樹紀錄了時間從 \([1, i]\) 的所有事件,
那就對於每個 \(i\) 就可以二分搜答案了!
持久化線段樹
實作
struct node {
node *left = NULL, *right = NULL;
int val;
};
實做
node* add(node* old, int pos, int val) {
node* res = new node(old), * now = res;
int l = 1, r = n, m;
res->val += val;
while (l < r) {
m = l + r >> 1;
if (pos > m) {
now->right = new node(old->right);
now->right->val += val;
now = now->right;
old = old->right;
r = m;
}
else {
now->left = new node(old->left);
now->left->val += val;
now = now->left;
old = old->left;
l = m+1;
}
}
return res;
}
實作
node* add(node* old, int pos, int val) {
node* res = new node(old), * now = res;
int l = 1, r = n, m;
res->val += val;
while (l < r) {
m = l + r >> 1;
if (pos > m) {
now->right = new node(old->right);
now->right->val += val;
now = now->right;
old = old->right;
r = m;
}
else {
now->left = new node(old->left);
now->left->val += val;
now = now->left;
old = old->left;
l = m+1;
}
}
return res;
}
例題
POJ2104
靜態區間第 \( K \) 大
TIOJ 1975
有兩種工作,總共有 n 個
第一種會佔用一個處理器 使用從 \(l_i\) 到 \(r_i\) 的所有時間 並且從頭到尾只能使用同一個處理器
第二種有完成期限,可以分配給不同的處理器,必須在 \(d_i\)之前完成,需要花 \(w_i\) 的時間
請問至少需要幾個處理器 才能完成所有工作
NOTE : 一個處理器在任何時刻都只能處理一個工作
第二種工作在任何時刻也最多只能被一個處理器處理
\(l_i \leq\ r_i \leq 10^6\)
\(n \leq 10^5\)
TIOJ 1840
帶修改區間 \(K\) 大
BIT +
動態開點值域線段樹
struct bit {
node* root[maxn];
void add(int x, int y, int val) {
for (;x <= maxn;x += x & -x)
modify(root[x], y, val);
}
};
struct bit{
void shift(vector<node*> &nodes, int dir) {
static const l_type = 0;
for (auto &i : nodes) i = (dir == l_type ? i->left : i->right);
}
int left_sum(vector<node*> &nodes) {
int res = 0;
for (auto i : nodes) res += i->left->cnt;
return res;
}
int query(int l, int r, int k) {
vector<node*> lnode, rnode;
for (int i = l;i;i ^= i & -i) lnode.pb(root[i]);
for (int i = r;i;i ^= i & -i) rnode.pb(root[i]);
int L = 1, R = n, M;
while (L < r) {
M = L + R >> 1;
if (int lcnt = left_sum(rnode) - left_sum(lnode) ; lcnt >= k) {
shift(rnode, 0), shift(lnode, 0);
R = M;
}
else {
k -= lcnt;
shift(rnode, 1), shift(lnode, 1);
L = M+1;
}
}
return L;
}
};
最長遞增子序列 LIS
map 維護單調隊列
\(dp_i := \) 以數值 \(i\) 結尾最長的答案
用 map<int,int> dp;
有 \(q, (q \leq 10^5)\) 筆操作
- 加進一筆資料 \(x, y, w, (x \leq 10^5, y \leq 10^5, w \leq 10^9)\)
- 詢問 \(a, b\) :
輸出在所有資料中 \(x \leq a, y \leq b\) 中最大的 \(w\)
最後一題
在碼頭上,你擁有一個碼頭,根據政府規定,一個碼頭一天最多只能有兩艘船停靠卸貨,你手上有一份名單上面有
\( n \leq 10^5 \) 個資訊,告訴你今天所有船的
停靠時間,離開時間,以及獲利
\(l_i, r_i, c_i, (l_i \leq r_i \leq 10^5, c_i \leq 10^9)\)
在任意時刻,一個碼頭最多都只能停靠一艘船,你可以選擇要不要讓他停靠,請問你今天最多能夠獲利多少呢?
資料結構們
By Kevin Zhang
資料結構們
- 1,439



