siZZle & DBAC
(Double-Bracket Algorithmic Cooling)
Kay Giang - NTU Singapore
DBAC Summary
QITE formula
|\Psi(\tau)\rangle = \frac{e^{-\tau \hat{H}}}{\|e^{-\tau \hat{H}}|\Psi(0)\rangle\|} |\Psi(0)\rangle
\(\Psi(0)\): Initial state
\(\Psi(\tau)\): State at time \(\tau\)
\(\hat H\): Diagonalised Hamiltonian
Cool the initial state \(\Psi(0)\) with respect to the Hamiltonian \(\hat H\)
Recursion step
\ket{\Psi(t)}\approx e^{t[\Psi(0),\hat H]}\ket{\Psi_0}
For short duration t:
\partial_\tau {|\Psi(\tau) \rangle} = [\Psi(\tau),\hat{H}] |\Psi(\tau) \rangle\
This motivates defining the recursion step:
\ket{\psi_{k+1}} = e^{t_k[\psi_k,\hat H]} \ket{\psi_k}
\(\ket{\psi_k}\): State at step \(k\)
DB-QITE recursion formula
\boxed{\ket{\psi_{k+1}} \approx e^{i\sqrt{t_k}\hat H} e^{i\sqrt{t_k}\psi_k}
e^{-i\sqrt{t_k}\hat H}\ket{\psi_k}}
e^{t[\psi,\hat H]}|\psi\rangle =
e^{i\sqrt{t}\hat H}e^{i\sqrt{t}\psi}
e^{-i\sqrt{t}\hat H}
e^{-i\sqrt{t}\psi}|\psi\rangle + \mathcal O(t^{3/2})
Using the group commutator relation:
DB-QITE recursion formula:
Density matrix exponentiation (DME)
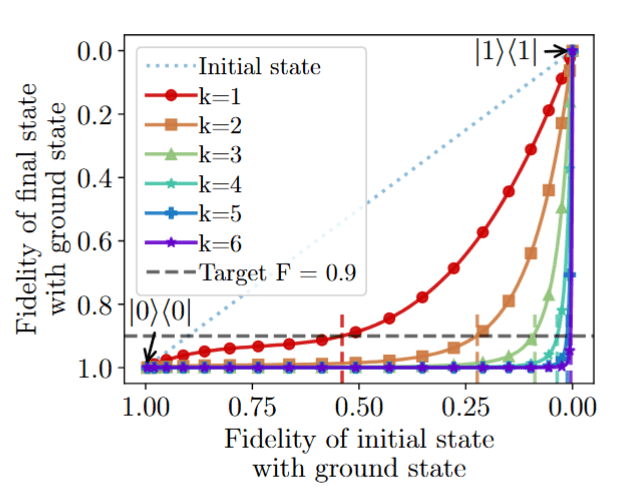
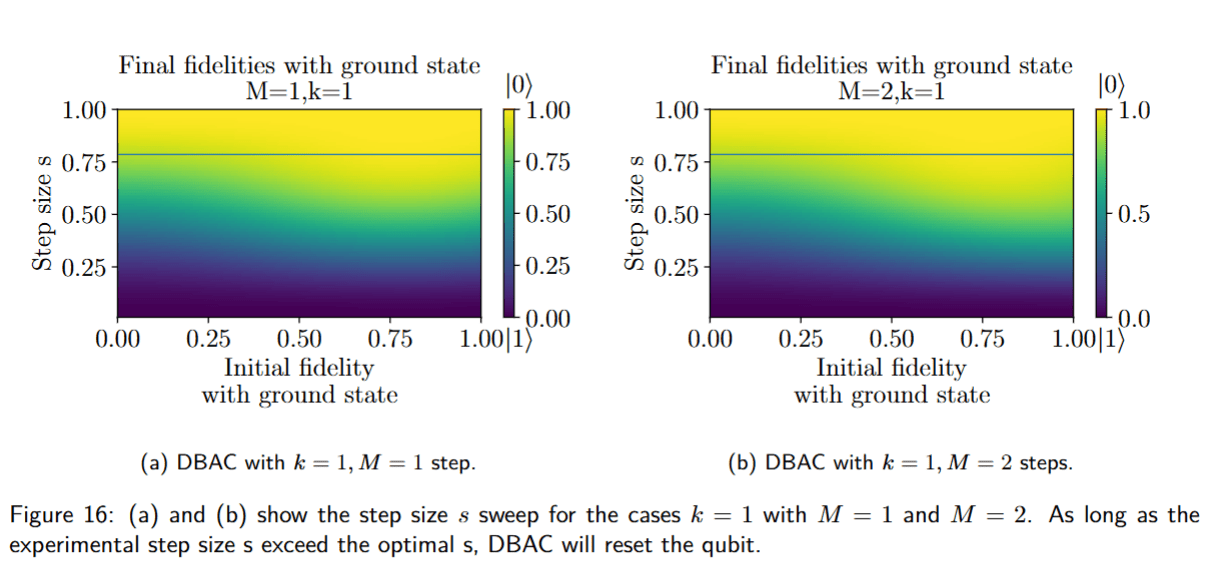
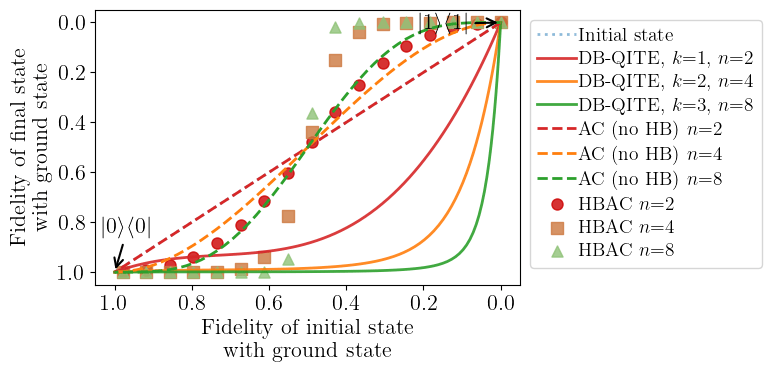
DB-QITE Performance
\boxed{\ket{\psi_{k+1}} \approx e^{i\sqrt{t_k}\hat H} e^{i\sqrt{t_k}\psi_k}
e^{-i\sqrt{t_k}\hat H}\ket{\psi_k}}
If we have ideal DME
\(e^{i\sqrt{t_k}\psi_k}\)
Data Taking
Part 1: siZZle and DME
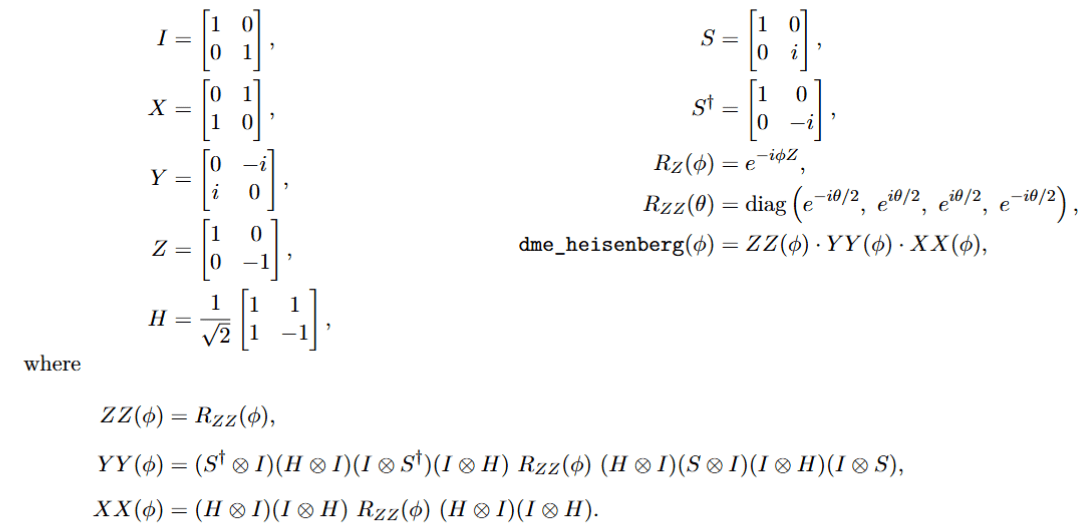
Gate defintion
ZZ PTM
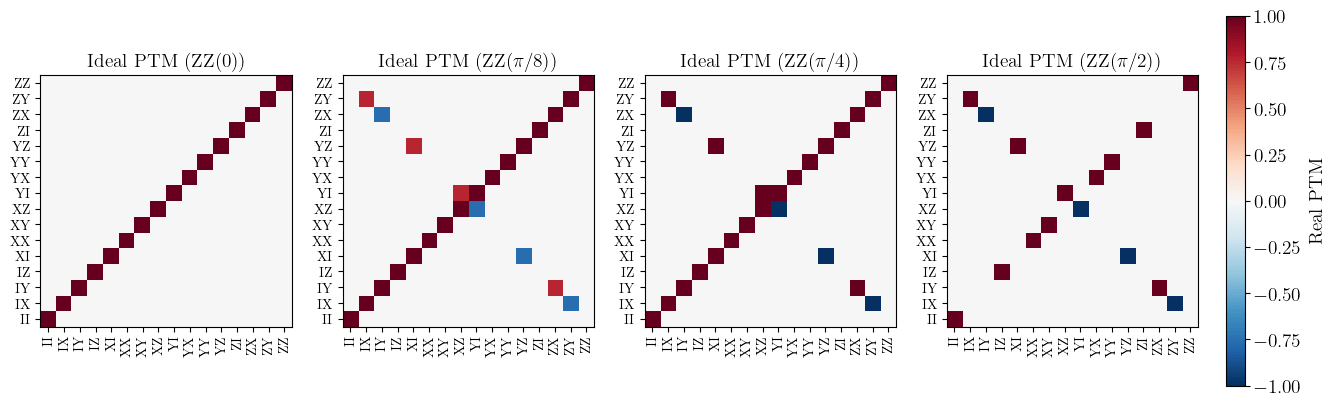
DME PTM
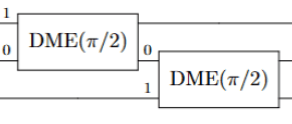
- DME\((\pi/2)\) is also just a full SWAP
- "Trotterization": \(N\times\)DME\((t/N) \to e^{i|\psi\rangle\langle\psi|}\)
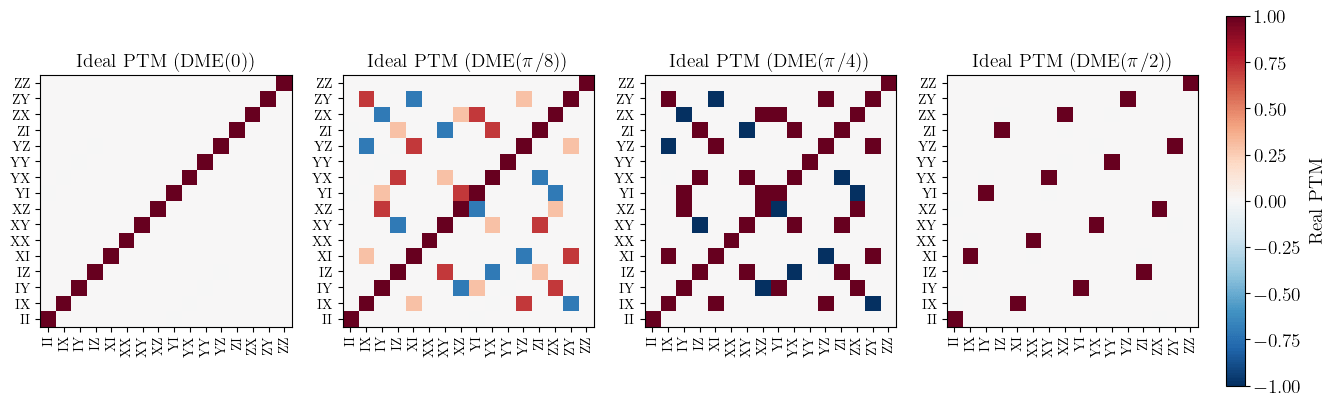
Sanity check: Compare DME
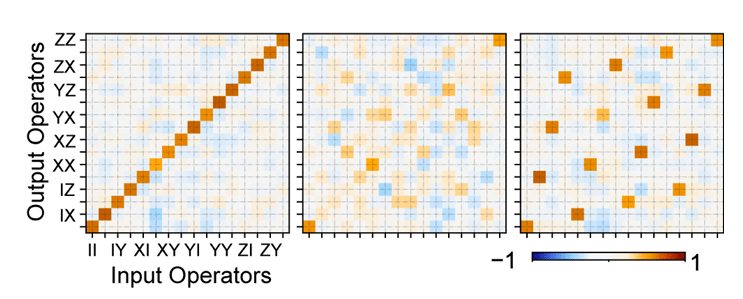
Our DME simulation
Data Taking
Part 2: Circuits PTM
Circuits PTM
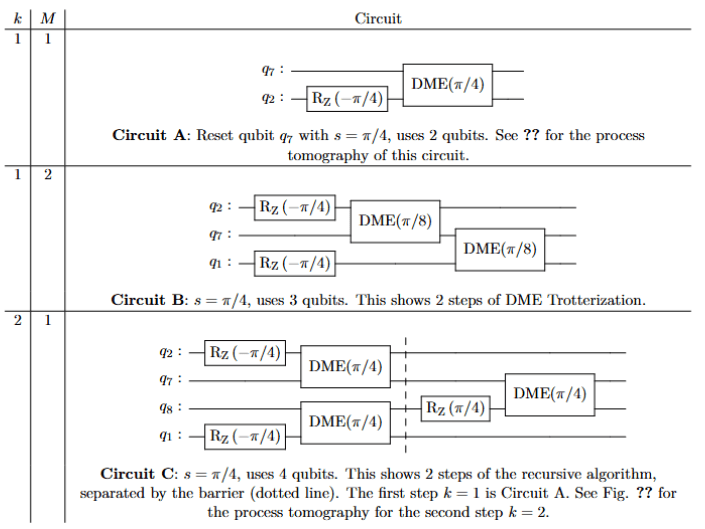
3 cases to take data:
- A - 2 qubits
- B - 3 qubits
- C - 4 qubits
R_Z(\phi) = e^{-i \phi Z} =
\begin{pmatrix}
e^{-i\phi} & 0 \\
0 & e^{i\phi}
\end{pmatrix}
Step size
Circuit A and C
Circuit B
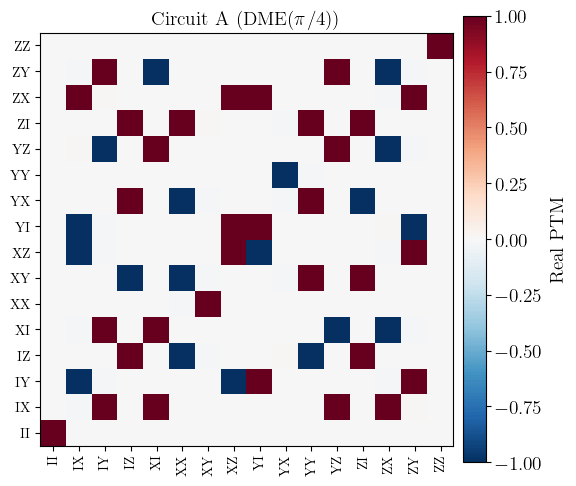
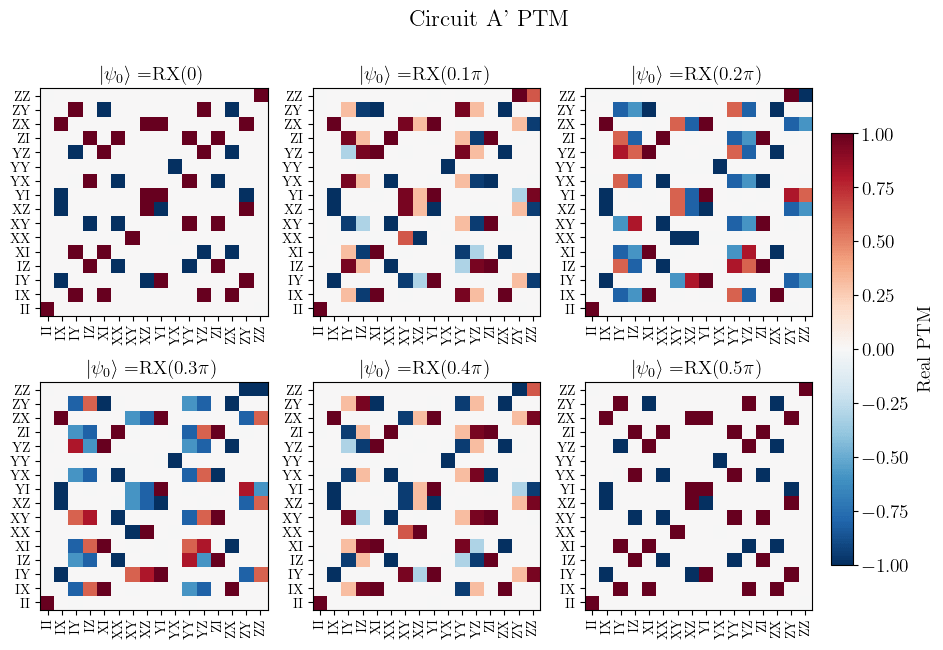
Circuit A PTM
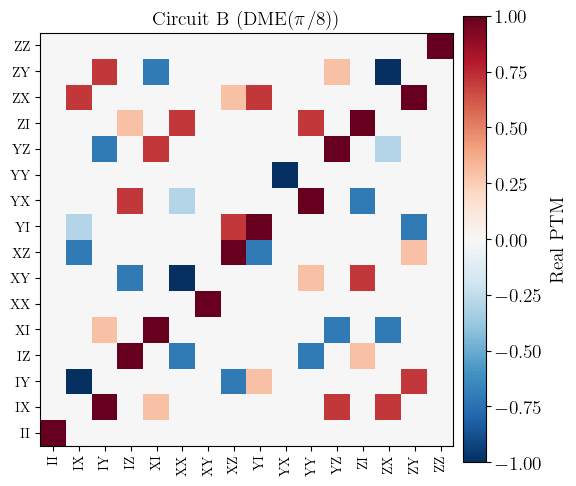
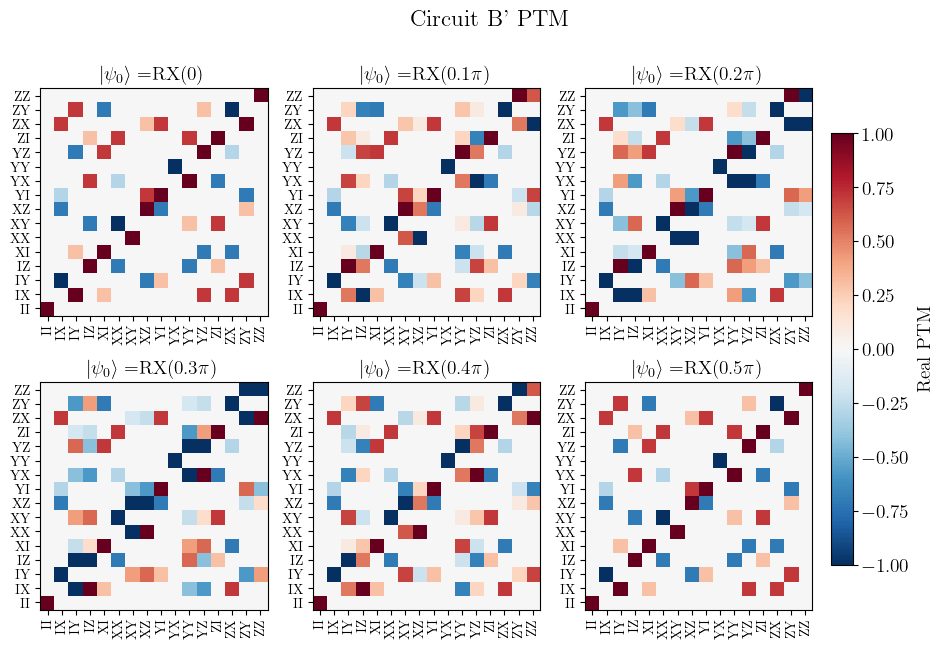
Part of circuit B PTM
Circuit C
(no need to do because it is Circuit A)
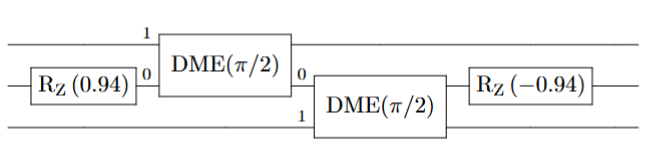
This is the first recursive use of DME.
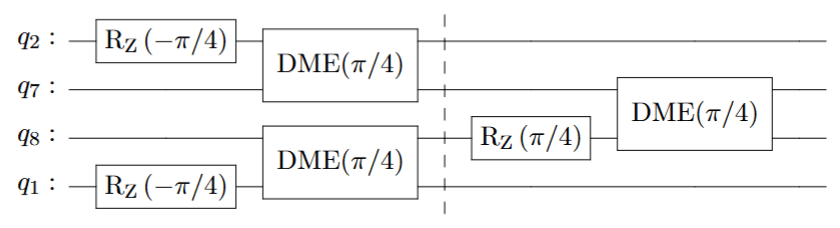
Data Taking
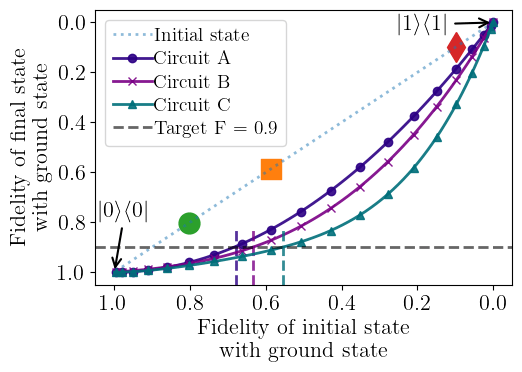
Part 3: Extended circuits PTM (Main result)
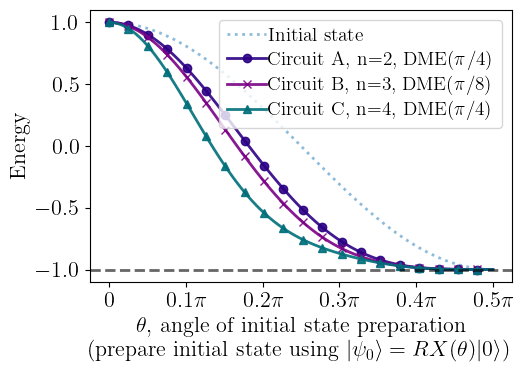
Main Result
(Energy drop of DB-QITE)
Take data on a grid of angles to reproduce this plot
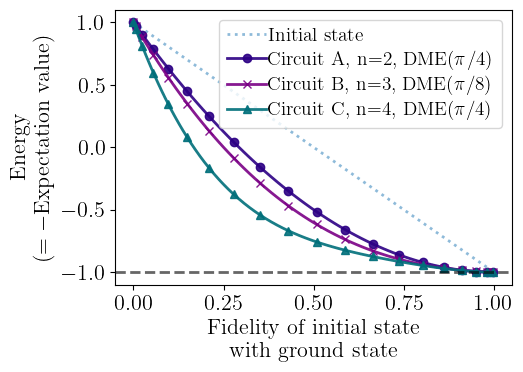
Main Result
(Energy drop of DB-QITE)
Same as previous plot but with initial fidelity instead of angle
From the previous plot, I will calculate this plot. This is our main result.
Circuit A'
(Circuit A with qubit initialisation)
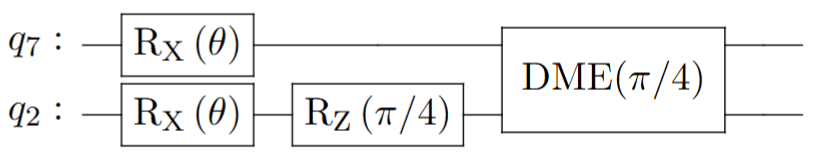
Circuit A'
Part of circuit B'
(similar to A' but with DME\((\pi/8)\))
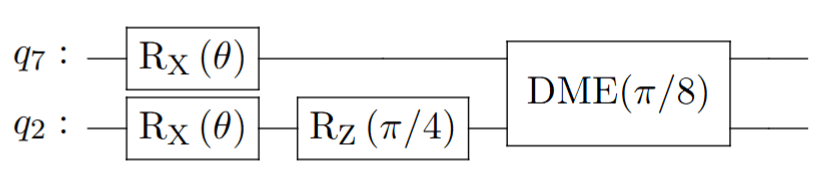
Part of circuit B'
Bloch Sphere
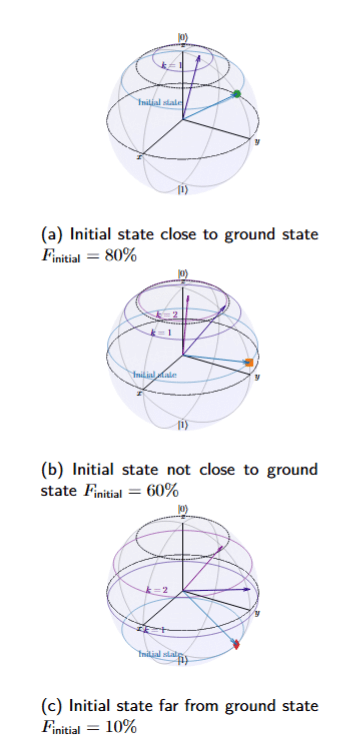
How to benchmark DME
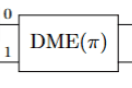
is the hardware definition of
2 approaches:
(Hardware focus) Compare to state of the art (Kjaegaard) who do QME
Problem: Kjaegaard has 2 qubits in 3D cavity with great fidelity \(\to\) they can do 30 CNOTs
(Alternatively) Comparing 2 times DME\((\pi/2)\) against DME\((\pi)\)
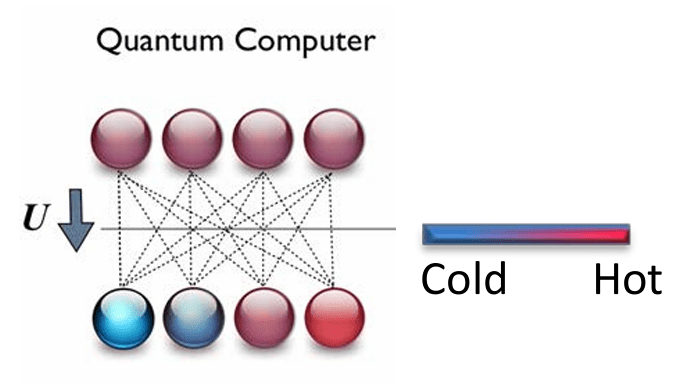
Algorithmic Cooling
What is algorithmic cooling (AC)?
-
Goal: Reduce entropy computational qubits.
-
Method: Iteratively apply a unitary entropy compression operation, UUU on all qubits, which is global and complicated
-
Process:
-
Redistributes entropy across all qubits.
-
Pushes entropy onto mmm reset-helper qubits.
-
Leaves computational (data) qubits colder, reset-helper qubits hotter.
-
Heat Bath Algorithmic Cooling
- Similar to Algorithmic Cooling
- BUT the Reset-helper qubit can come into contact with the bath and rethermalize (ie reset itself)
- The popular, well-known method
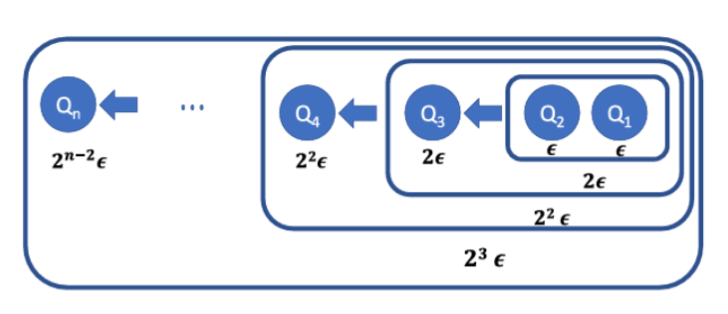
Q1: reset qubit
- Compress entropy of Q2 into Q1
- Q1 came in contact with bath
- Compress entropy of Q3 into Q1, Q2
- Q1 came in contact with bath
- Compress entropy of Q2 into Q1
HBAC vs DB-RESET
- Cool state towards eigenstate
- Cool state towards ground state
HBAC
DB-RESET
Heat bath algorithmic cooling
- Requires a bath
- Complicated compilation of U
- Using a full SWAP operation
- 3 qubits: require 2 full SWAP, 4 CNOT, 1 Toffoli
- Requires no bath
- Simple decomposition
- Partial SWAP using hardware-natural decomposition \(\to\) faster:
- 3 qubits: require 3 full ZZ gate
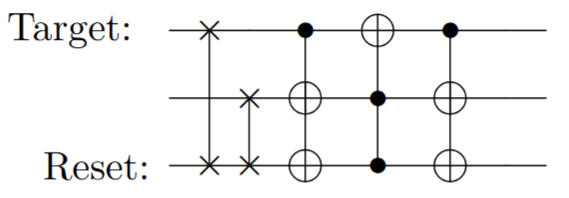
HBAC vs DB-RESET
HBAC
DB-RESET
Heat bath algorithmic cooling
- Works on any state
- Cools an ensemble of qubits
-
Can operate on mixed states, needs dephasing
- Only works on pure states
- Cools one qubit
- Doesn't need dephasing, can operate on state with coherence but must be pure
HBAC vs DB-RESET
Both: Building a hierachy of baths that gets colder
HBAC
DB-RESET
Heat bath algorithmic cooling
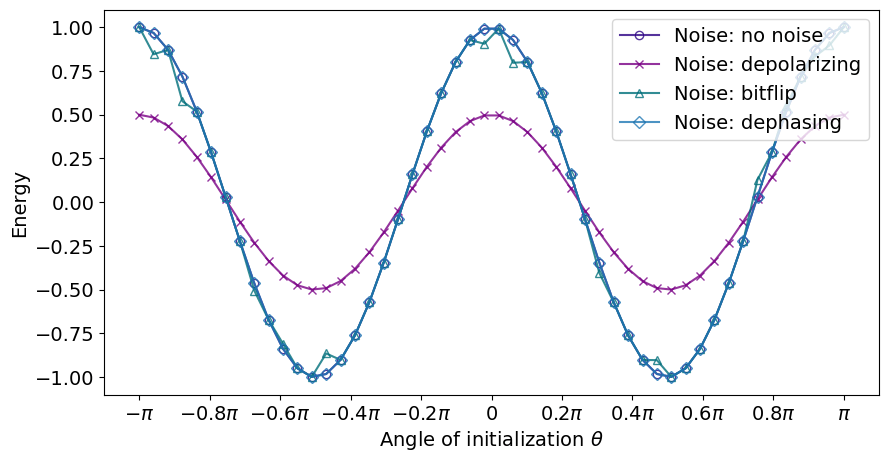
DBAC on mixed state
DBAC on mixed state
Even if the state is not arbitrarily pure, DBAC can reduce energy
DB-QITE on mixed state
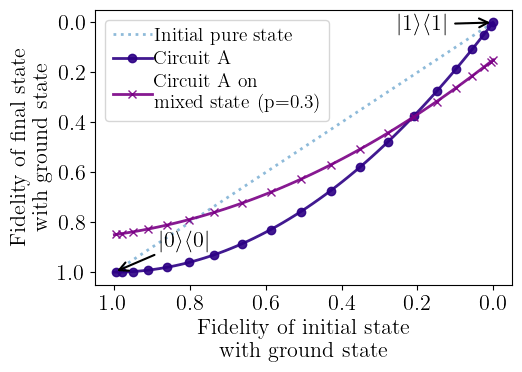
Still need purification to work well on mixed state
DB-QITE on mixed state
Pure
Mixed
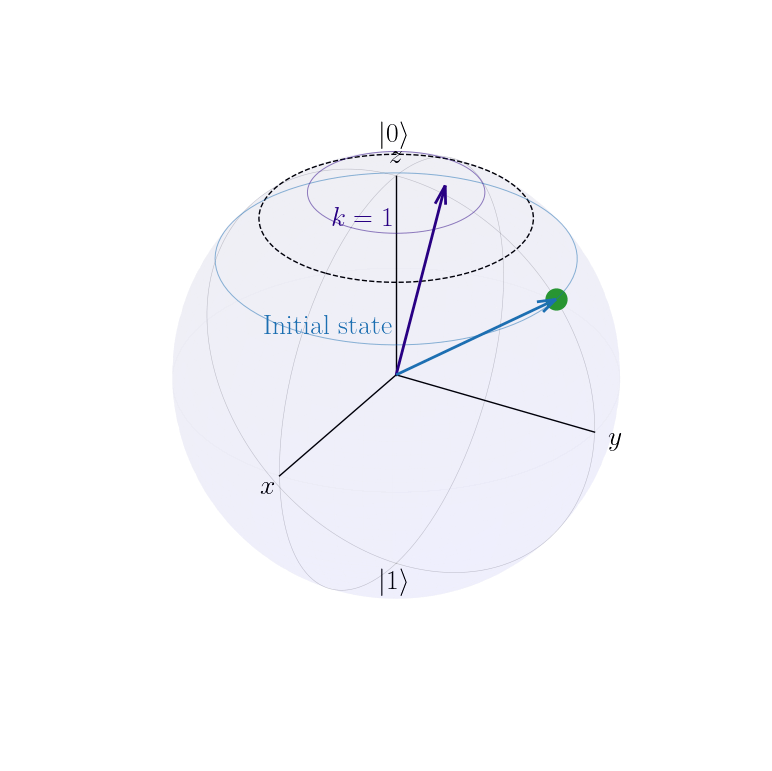
Initial state lies on Bloch sphere surface
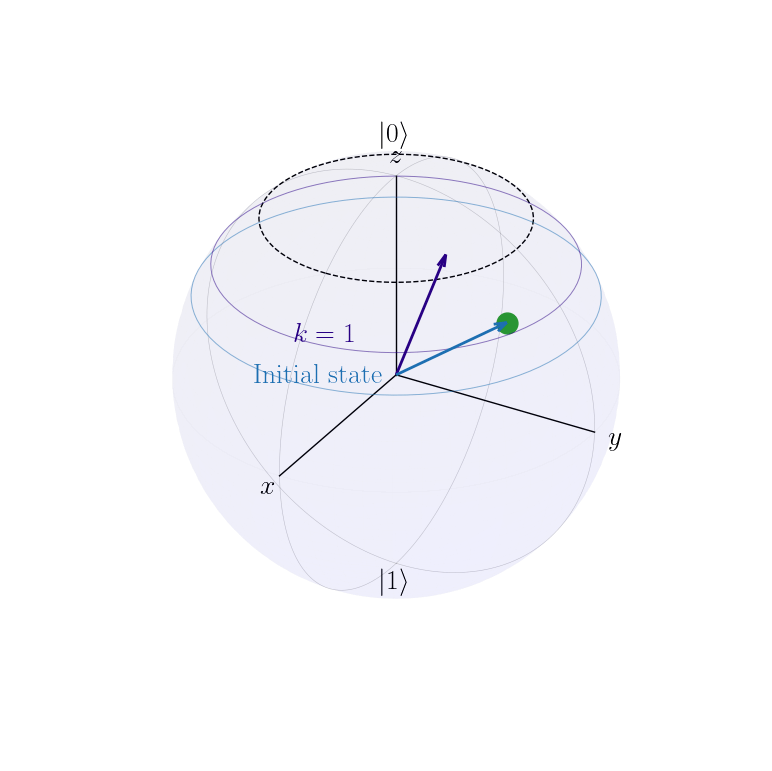
Initial state lies inside Bloch sphere
DBAC brings state inside dotted line
(F=0.9)
DBAC brings state closer to \(|0\rangle\) but not inside dotted line (ie more diagonal but still not pure)
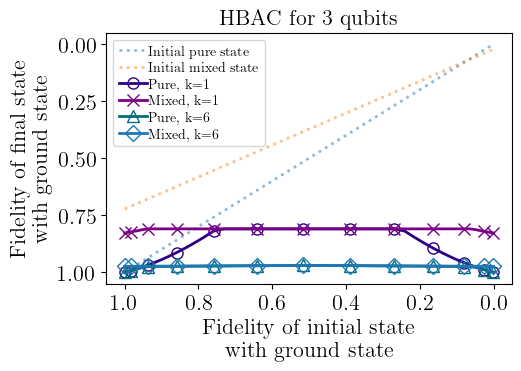
DBAC vs HBAC on mixed state
NMR experiments: 3 qubits, 6 steps
See purple and dark purple lines:
Pure and mixed state with 1 step
DBAC
Discussion
Energy reduction
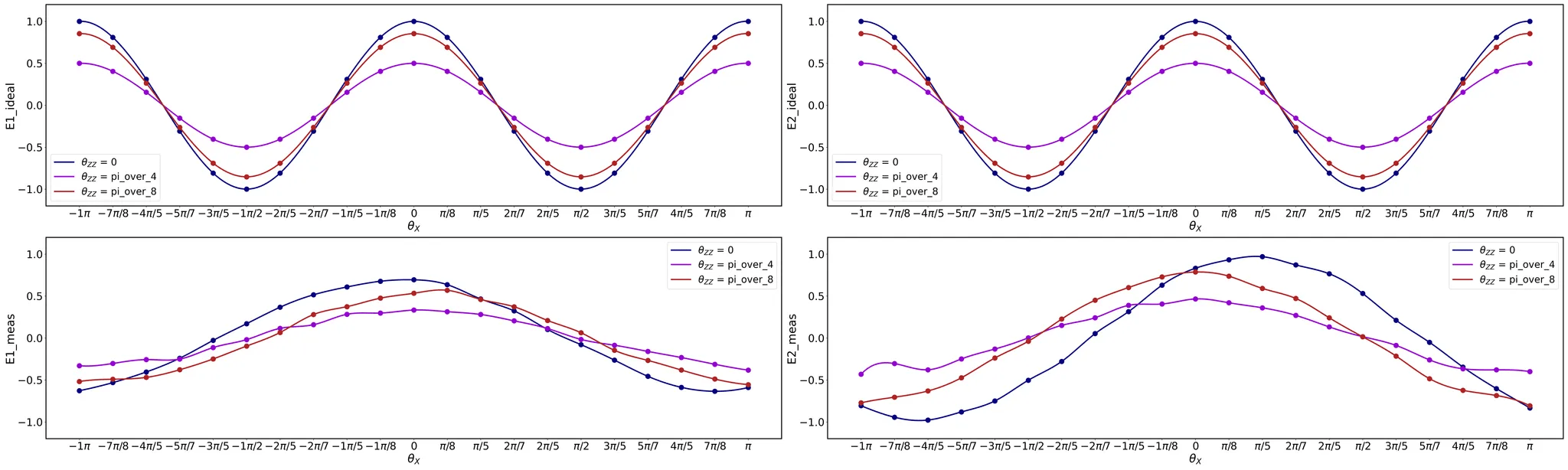
Different 'period'?
|0\rangle
Energy reduction
Possible causes:
- Depolarising \(\to\) No, Kay has checked
- Wrong RX gates between experiment and simulation \(\to\) No, because DME (that uses RX) works
Behaviour is consistent across multiple qubit sets
Unused slides
Hardware
- Show new Hardware
- siZZle Gate
- siZZle Compilation for DME: Make DME more natural
- First DME with \(n \neq 2\)
Algorithms
- A working example of QDP
- DB-QITE — New Reset Method using DME
- DB-QITE fill a gap left by HBAC
Topics currently covered
Overview of QDP (Quantum Dynamic Programming)
- Usual quantum computing is static: To change operation, we have to change the circuit
- Dynamic quantum computing: To change operation, only need to change instruction qubit
Normal way we do quantum computing: Static
Dynamic Quantum Computing
Kjaergaard et al., arxiv:2001.08838
DBAC Experiment roadmap
By Khanh Uyen Giang
