DBAC: Double-bracket Algorithmic Cooling
- About me
- Double-bracket Quantum Imaginary Time Evolution (QITE)
- DBAC Compilation for single qubit
- Quantum Dynamic Programming
Kay Giang - NTU
Master and Bachelor at University of Oxford
- Thesis was in Astrophysics
- Coursework in Quantum Information
Research Assiant at Nanyang Technological University in Singapore
- Multidisciplinary projects - theory, numeric and experimental
- DB-RESET: Algorithmic cooling using double-bracket
About me
Khanh Uyen (Kay) Giang
Outside physics, I enjoy watercolor art, pottery and ice-skating
Double-bracket Quantum Imaginary Time Evolution
(DB-QITE)
Gluza et al., arxiv:2412.04554
QITE formula
|\Psi(\tau)\rangle = \frac{e^{-\tau \hat{H}}}{\|e^{-\tau \hat{H}}|\Psi(0)\rangle\|} |\Psi(0)\rangle
\(\Psi(0)\): Initial state
\(\Psi(\tau)\): State at time \(\tau\)
\(\hat H\): Diagonalised Hamiltonian
Cool the initial state \(\Psi(0)\) with respect to the Hamiltonian \(\hat H\)
DB-QITE formula
|\Psi(\tau)\rangle = \frac{e^{-\tau \hat{H}}}{\|e^{-\tau \hat{H}}|\Psi(0)\rangle\|} |\Psi(0)\rangle
Gluza et al. (2412.04554) shows that QITE satisfy:
\begin{align*}
\partial_\tau {|\Psi(\tau) \rangle} = [\Psi(\tau),\hat{H}] |\Psi(\tau) \rangle
\end{align*}
Double-bracket
\frac{\partial \Psi(\tau)}{\partial \tau} = \big[ [\Psi(\tau),\hat H],\Psi(\tau)\big]
In terms of the density matrix \(\Psi(\tau)\):
Recursion step
\ket{\Psi(t)}\approx e^{t[\Psi(0),\hat H]}\ket{\Psi_0}
For short duration t:
\partial_\tau {|\Psi(\tau) \rangle} = [\Psi(\tau),\hat{H}] |\Psi(\tau) \rangle\
This motivates defining the recursion step:
\ket{\psi_{k+1}} = e^{t_k[\psi_k,\hat H]} \ket{\psi_k}
\(\ket{\psi_k}\): State at step \(k\)
DB-QITE recursion formula
\ket{\psi_{k+1}} = e^{t_k[\psi_k,\hat H]} \ket{\psi_k}
\boxed{\ket{\psi_{k+1}} \approx e^{i\sqrt{t_k}\hat H} e^{i\sqrt{t_k}\psi_k}
e^{-i\sqrt{t_k}\hat H}\ket{\psi_k}}
e^{t[\psi,\hat H]} =
e^{i\sqrt{t}\hat H}e^{i\sqrt{t}\psi}
e^{-i\sqrt{t}\hat H}
e^{-i\sqrt{t}\psi} + \mathcal O(t^{3/2})
Using the group commutator relation:
DB-QITE recursion formula:
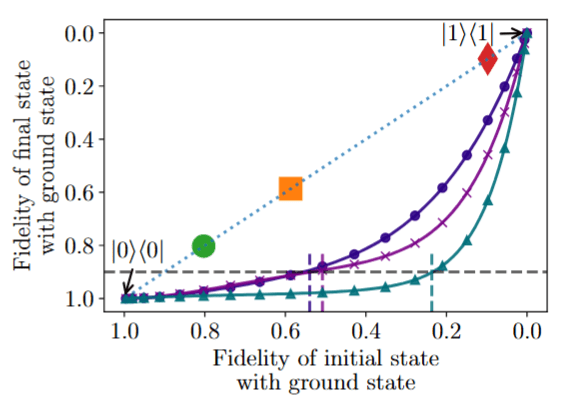
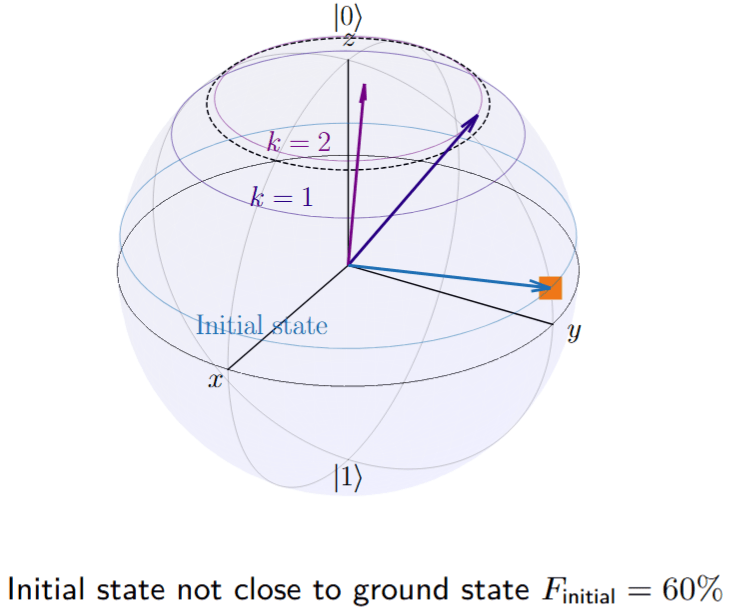
Fidelity increase guarantee
\boxed{\ket{\psi_{k+1}} \approx e^{i\sqrt{t_k}\hat H} e^{i\sqrt{t_k}\psi_k}
e^{-i\sqrt{t_k}\hat H}\ket{\psi_k}}
F_{k+1} \geq 1- (1- t F_0 \Delta)^{k}
Fidelity with ground state after step \(k+1\):
\(F_0\): fidelity between the initial state with ground state
\(\Delta\): spectral gap
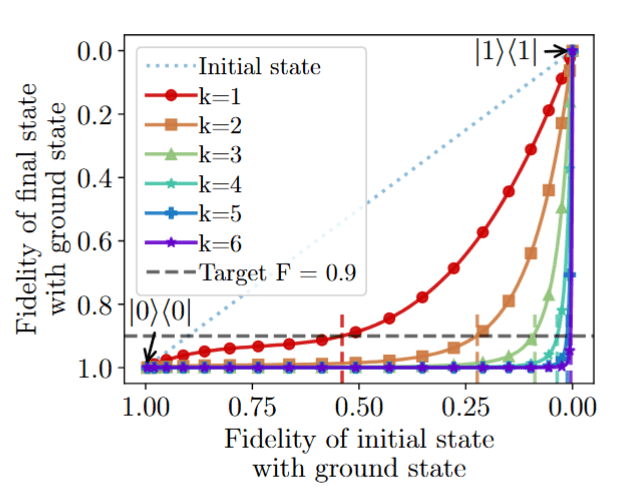
DB-QITE Performance
\boxed{\ket{\psi_{k+1}} \approx e^{i\sqrt{t_k}\hat H} e^{i\sqrt{t_k}\psi_k}
e^{-i\sqrt{t_k}\hat H}\ket{\psi_k}}
If we have ideal \(e^{i\sqrt{t_k}\psi_k}\)
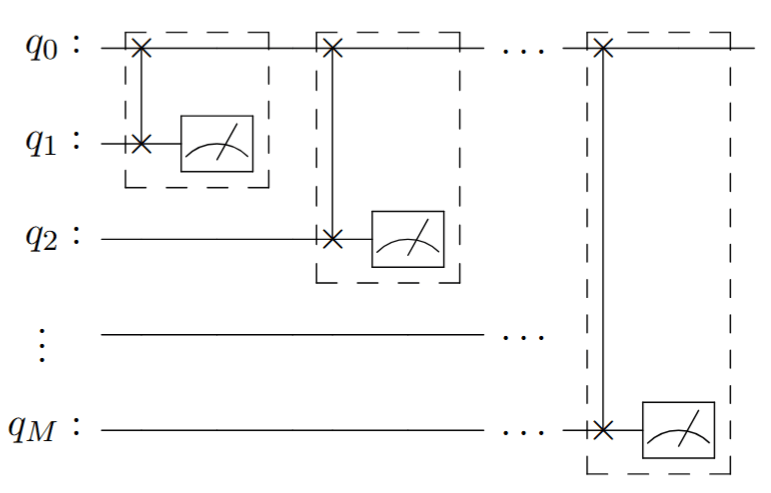
DBAC compilation for single qubit case
Compilation for resetting one qubit
\boxed{\ket{\psi_{k+1}} \approx e^{i\sqrt{t_k}\hat H} e^{i\sqrt{t_k}\psi_k}
e^{-i\sqrt{t_k}\hat H}\ket{\psi_k}}
\(e^{i\sqrt{t_k}\psi_k}\): Density matrix exponentiation (DME)
Single qubit: \(\hat H = \hat Z\)
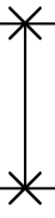
: \(\delta\)SWAP gate, applying \(e^{-i t \text{SWAP}}\). Compiled using Heisenberg interaction: \(e^{it(XX+YY+ZZ)}\)
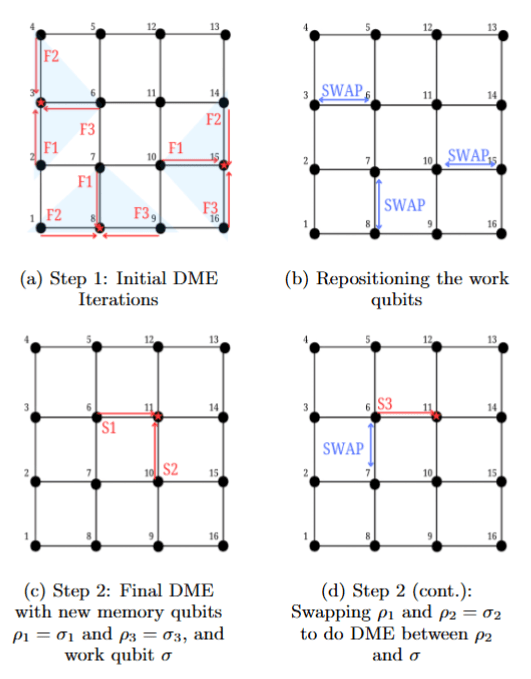
DME Circuit
\boxed{\ket{\psi_{k+1}} \approx e^{i\sqrt{t_k}\hat H} e^{i\sqrt{t_k}\psi_k}
e^{-i\sqrt{t_k}\hat H}\ket{\psi_k}}
\begin{align*}
\hat{E}_t^{(\rho)}(\sigma) &= \text{Tr}_{1}\left[e^{-i t \text{SWAP}}(\rho\otimes\sigma) e^{i t \text{SWAP}}\right]\\
&= \sigma - it[\rho,\sigma] +O(t^2)\\
&= e^{-it\rho} \sigma e^{it\rho} +O(t^2)
\end{align*}
Density matrix exponentiation
The DME channel is:
Repeating \(M\) iterations yields:
\left(\hat{E}_{(t/M)}^{(\rho)}(\sigma)\right)^{M} = e^{-it\rho} \sigma e^{it\rho} + O(t^2/M)
DME Circuit
- This DME protocol was introduced in Kjaergaard et al., arxiv:2001.08838
- In their paper, they use the 3 CNOT decompositions for the \(\delta\text{SWAP}\) gate, and performed it on only 2 qubits
- No literature has performed DME on more qubits
DME Circuit
\(\delta\)SWAP compiled using Heisenberg interaction: \(e^{it(XX+YY+ZZ)}\)
Reason for using ZZ interaction: The entangling operation in transmon qubit is Stark-induced ZZ by level excursions (siZZle)
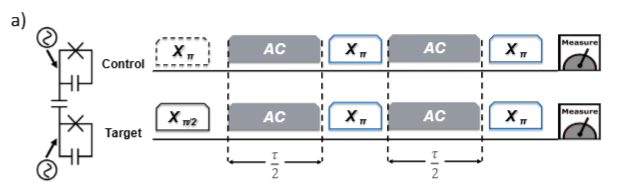
Example DBAC Circuits
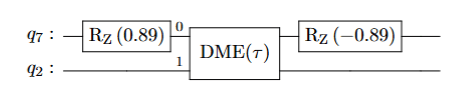
\(k=1\) recursion step (with optimized \(t_k\)):
\(k=2\) recursion steps:
\boxed{\ket{\psi_{k+1}} \approx e^{i\sqrt{t_k}\hat H} e^{i\sqrt{t_k}\psi_k}
e^{-i\sqrt{t_k}\hat H}\ket{\psi_k}}
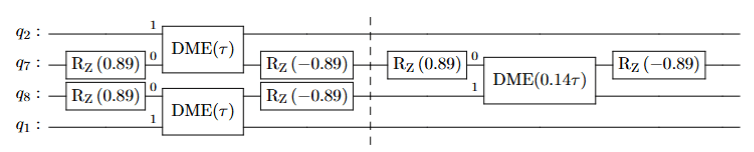
DBAC Performance
\(k=2\) recursion steps (3 copies of the reset qubit):
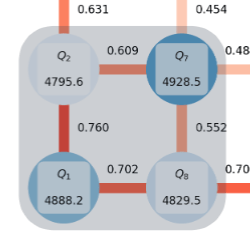
Qubit chip layout
Comparing DBAC with existing protocols
HBAC
- Work iteratively
- NMR/ solid state that have a thermal bath
- Work on any state
- Cool an ensemble of qubit
- Complex unitary decomposition
- Using a full SWAP operation
DBAC
- Work iteratively
- Superconducting system, does not use a bath
- Only work on pure states
- Cool one qubit
- Simple decomposition
- Partial SWAP using hardware-natural decomposition \(\to\) faster
Heat bath algorithmic cooling
Microwave drive
- High fidelity (99.5-99.8%)
- Duration: 500ns
- Hardware specific
- Lower fidelity
- Duration: ~200ns for 1 step
- General purpose
DBAC
Why DBAC?
- Enable qubit chip testing with clear interpretable results and exponential complexity
- Dynamic nature, allows repetition on varied qubit layout
- Proof of principle for a new class of algorithm: dynamic quantum algorithm
Quantum Dynamic Programming (QDP)
A framework that uses copies of the recursive state to implement the recursion step unitary
Static vs Dynamic
- Usual quantum computing is static: To change operation, we have to change the circuit
- Dynamic quantum computing: To change operation, only need to change instruction qubit
Normal way we do quantum computing: Static
Dynamic Quantum Computing
Kjaergaard et al., arxiv:2001.08838
Dynamic Quantum Algorithm
- Question 1: Can quantum information be the source code?
- Answer: Kimmel et al. (arxiv 1608.00281) shows that this model is basis of a universal model for quantum computation
Dynamic Quantum Algorithm
- Questions 2: What would QDP be good for?
-
Example:
- DB-RESET
- Provide a universal circuit that compute the Schmidt spectrum
- For well-behaved recursions, QDP yields accurate results with polynomial depth
Quantum Dynamic Programming
- QDP speed up recursion of the form (single memory call):
\[ U^{(\mathcal{N},\rho)} = V_2e^{i\mathcal{N}(\rho)}V_1\] where \(\mathcal{N}\) is any Hermitian-preserving map - Memory call: Idealized transformation we want to make. It asks for memory (instruction state \(\rho\)).
- General case:
- Problem: We can't implement this naturally in qunatum mechanics
Quantum Dynamic Programming
- Solution: QDP approximate this memory call unitary:
- QDP does this by using memory usage query:
where \(N\) is the operator of the memory usage query, the partial transpose of the Choi matrix corresponding to \(\mathcal{N}\)- Consume (trace out) an instruction state
- Repeat this procedure M times, we obtain
\mathcal{E}_s^{(N,\rho)}(\sigma) = Tr_\rho [e^{-iNs} (\rho\otimes\sigma) e^{iNs}]
E^{(\mathcal{N},\rho)}(\sigma) = e^{i\mathcal{N}(\rho)} \sigma e^{-i\mathcal{N}(\rho)}
\mathcal{E}^{(\mathcal{N},\rho,M)}_{QDP} \coloneqq (\mathcal{E}^{(\mathcal{N},\rho)}_{1/M})^M = E^{(\mathcal{N},\rho)} + O(1/M)
Quantum Dynamic Programming
Example: Density Matrix Exponentiation
- Memory call unitary:
\[E^{(\mathcal{N},\rho)}(\sigma) = e^{i\rho\theta} \sigma e^{-i\rho\theta}\] - Memory call operator: \[\mathcal{N}\rho = \rho \to \mathcal{N} = id\]
- Memory usage query operator: \[N = \delta SWAP\]
- Memory usage query: \[\sigma\to\text{Tr}_\rho[e^{-i\text{SWAP}\delta}(\sigma\otimes\rho) e^{i\text{SWAP}\delta}]\]
Quantum Dynamic Programming
Example: Oblivious Schmidt decomposition
- Bipartite pure state \(|\psi\rangle\) has a Schmidt decomposition:
|\psi\rangle_{AB} = \sum_j \sqrt{\lambda_j} |\phi_j\rangle_A|\chi_j\rangle_B
- Double bracket iteration of OSD:
e^{i\mathcal{N}(\psi_n)} = e^{s_n[D,\rho_n^{(A)}]}\otimes \mathbb{I}_B
- Memory usage query:
- Memory usage query operator:
Summary
- DB-QITE: formulate a recursion relation that implement imaginary time evolution
- DBAC: synthesizes a circuit that reset 1 qubit iteratively
- Quantum dynamic programming (QDP): uses copies of the instruction state to implement the operation
Thank you for listening!
Expanding the landscape of 1D Bose gas experiment
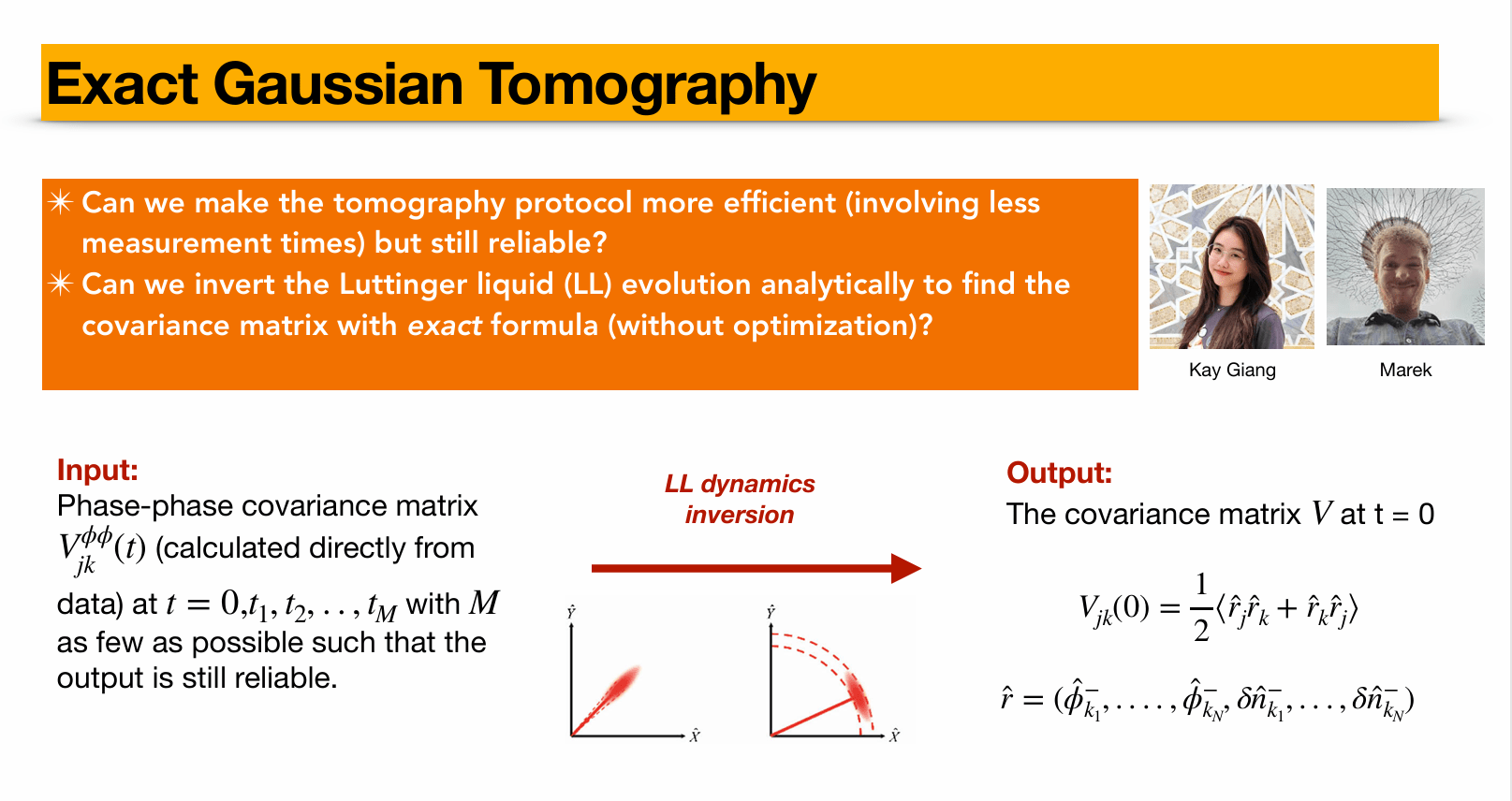
Full exact Gaussian Tomography
DBAC Theory
By Khanh Uyen Giang
