Programming
Multi-core
and
Many-core Systems
Assignment 1
Jonas Theis
Kian Paimani
February 2018
Goals
- Implement an optimized sequential version
- Compile it with different flags and tools
- Implement a manually vectorized version using Intel SSE
- Compare, benchmark and evaluate both
Sequential Version
- Code Motion - Share common expression
for (int row_idx = 0; row_idx < N; row_idx++) {
for (int col_idx = 0; col_idx < M; col_idx++) {
matrix[row_idx*M + col_idx] = computed_new_value;
}
}int current_row_idx;
for (int row_idx = 0; row_idx < N; row_idx++) {
current_row_idx = row_idx*M
for (int col_idx = 0; col_idx < M; col_idx++) {
matrix[current_row_idx + col_idx] = computed_new_value;
// update diff etc.
}
}
}Sequential Version
- Code Motion - Share common expression
int current_row_idx, current_cell_index;
for (int row_idx = 0; row_idx < N; row_idx++) {
current_row_idx = row_idx*M
for (int col_idx = 0; col_idx < M; col_idx++) {
current_cell_index = current_row_idx + col_idx
matrix[current_cell_index] = computed_new_value;
// update diff etc.
int diff = matrix[current_cell_index] - o_matrix[current_cell_index]
}
}
}Sequential Version
- Avoiding Optimization Blockers
- Function calls
- Conditions
for (int row_idx = 0; row_idx < N; row_idx++) {
for (int col_idx = 1; col_idx < M-1; col_idx++) {
matrix[row_idx*M + col_idx] = computed_new_value;
}
// do cell update for col_idx = 0
matrix[row_idx*M] = computed_new_value;
// do cell update for col_idx = M-1
matrix[row_idx*M + M-1] = computed_new_value;
} Sequential Version
-
Avoiding Optimization Blockers
- Removing another subtle conditional statement
// diff = t_surface_index - temp_index;
// abs_diff = diff > 0 ? diff : diff * -1;
union Abs {
double d;
long i;
};
const long abs_bitmask = ~0x8000000000000000;
// calculate absolute diff between new and old value
abs_diff.d = t_surface_index - temp_index;
abs_diff.i = abs_bitmask & abs_diff.i;Sequential Version
- Memory Access Pattern
int current_row_idx, current_cell_index;
for (int row_idx = 0; row_idx < N; row_idx++) {
current_row_idx = row_idx*M
for (int col_idx = 0; col_idx < M; col_idx++) {
current_cell_index = current_row_idx + col_idx
matrix[current_cell_index] = computed_new_value;
// update diff etc.
int diff = matrix[current_cell_index] - o_matrix[current_cell_index]
}
}
}Sequential Version
- Memory Access Pattern
int current_row_idx, current_cell_index, temp_value;
for (int row_idx = 0; row_idx < N; row_idx++) {
current_row_idx = row_idx*M
for (int col_idx = 0; col_idx < M; col_idx++) {
current_cell_index = current_row_idx + col_idx
temp_value = computed_new_value;
// update diff etc.
int diff = temp_value - o_matrix[current_cell_index]
// write to memory once
matrix[current_cell_index] = temp_value
}
}SIMD Version
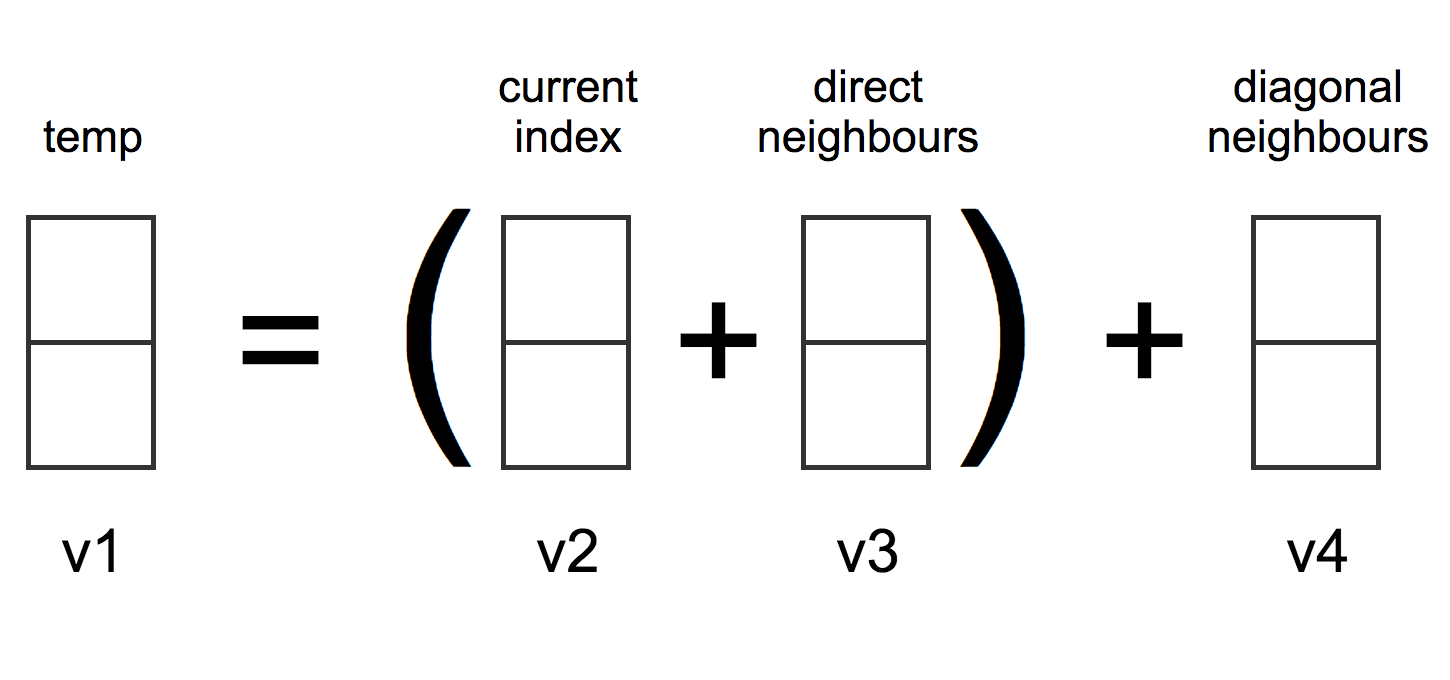
Evaluations
Sequential - Different size
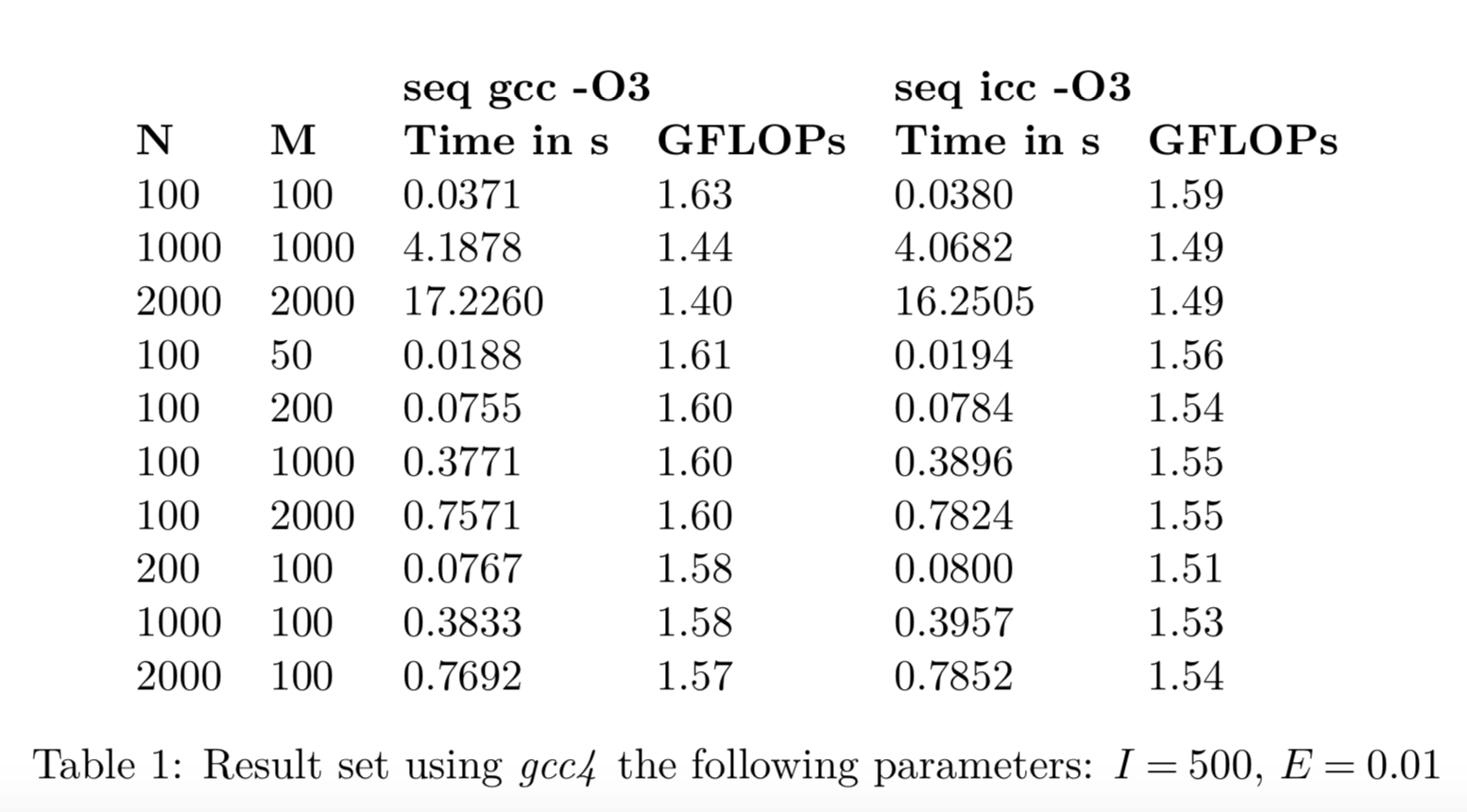
Evaluations
Sequential Different Compilers



Evaluations
Vectorized version


Conclusions
-
There is a noticeable difference between the choice of compiler version.
-
Recent versions of compilers do a better job at optimizing the code.
-
While our vectorized version could outperform gcc4 and icc, gcc6 still produced a faster executable for the sequential version.
-
-
failed attempt at vectorizing a sequence of additions => SSE can handle only up to 2 double values. Not always worth the time!
pmms-1
By Kian Peymani
pmms-1
- 575



