⾮線形カオス⼒学系の時系列状態推定と誤差解析
○竹田 航太 (名古屋大学), 坂上 貴之 (京都大学)
This was supported by RIKEN Junior Research Associate Program and JST SPRING JPMJSP2110.
(T.+2024) K. T. & T. Sakajo, SIAM/ASA Journal on Uncertainty Quantification, 12(4), 1315–1335.
(T. 2025) K. T., Error Analysis of the Ensemble Square Root Filter for Dissipative Dynamical Systems, PhD Thesis, Kyoto University, 2025.
自己紹介：竹田 航太
研究キーワード：データ同化，流体力学，不確実性定量化
これまで．．．
日本数学会，
日本応用数理学会，
応用数理学会（アメリカ），
アメリカ統計学会
日本の統計関連学会にも
進出したい
テーマの親和性は高いはず
個人サイトで講演資料を公開中 ↓
所属：名古屋大学工学研究科・理研計算科学センター
イントロ：気象予測とカオス性
数値気象予測では，流体方程式を含む非線形力学モデルを用いる
長期予測が困難
台風のアンサンブル予報と予報円
\partial_t \bm{u} + (\bm{u} \cdot \nabla) \bm{u} = - \frac{1}{\rho} \nabla p + \nu \triangle \bm{u} + \bm{f} \text{ \& } \dots
小さい初期誤差が
指数的に拡大
気象状態
time
実際の状態
数値予測
カオス
イントロ：非線形カオス力学系
小さい初期誤差 → 予測で拡大 → 無情報
3次元力学系によるモデル化 ↓
イントロ：観測
対象とする系：非線形カオス力学系
観測時系列：ノイズを含む，部分的な情報
(x,y,z)\mapsto(x,y)
観測ノイズ
部分観測
カオス
本講演で扱う
本講演で扱わない
観測時系列
状態時系列
→ 予測が無情報になる前に観測値で修正したい
イントロ：データ同化
観測ノイズ
「現実」
観測値
y_n = H u_n + \eta_n
(u_n)_n
観測
モデル
カオス
生成
u_n = \Psi(u_{n-1})
法則はわかるが予測困難
推定誤差
推定値
(v_n)_n
データ同化
高精度
高解像度
イントロ：データ同化
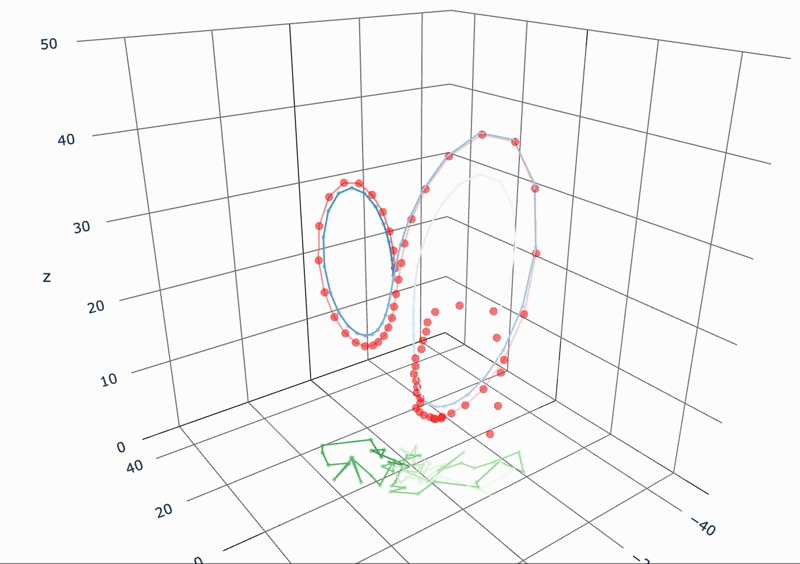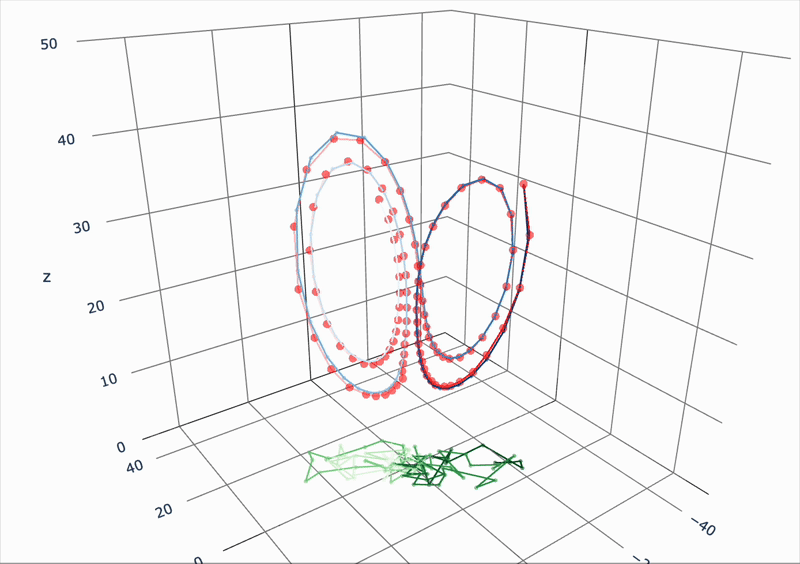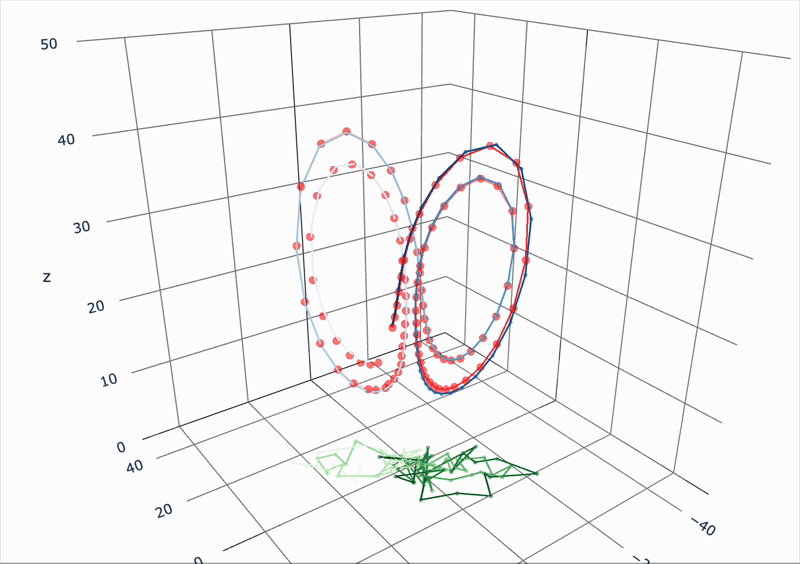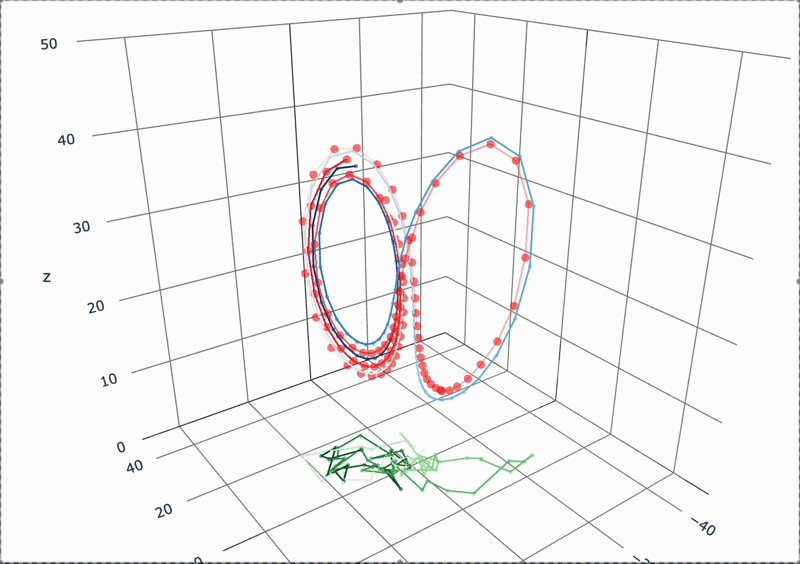
緑：観測時系列
青：「真」の状態時系列
赤：推定値の時系列
非線形カオス力学系の時系列推定
目次：準備
観測ノイズ
「現実」
観測値
y_n = H u_n + \eta_n
(u_n)_n
観測
モデル
カオス
生成
u_n = \Psi(u_{n-1})
推定誤差
推定値
(v_n)_n
データ同化
まず，設定を詳しく説明
準備：モデル（一般）
\frac{d u}{dt} = \mathcal{F}(u)
(\mathcal{F}: \R^{N_u} \rightarrow \R^{N_u}, u(0) = u_0 \in \R^{N_u})
\Psi_t (u_0) = u(t; u_0)
モデル
解写像
\R^{N_u} (N_u \in \mathbb{N})
書き換え
(\Psi_t : \R^{N_u} \rightarrow \R^{N_u}, t \ge 0)
: 状態空間
モデル：既知，初期値：未知
t
真の解
未知
※ 確率微分方程式や偏微分方程式に基づく定式化もあるが触れない．
既知
大前提：真の状態はよく知られた法則に従う．
準備：観測（一般）
離散時間モデル
\mathbb{R}^{N_u}
\Psi = \Psi_\tau, \tau > 0
t
y_n = H u_n + \eta_n, \quad n \in \mathbb{N}.
H \in \mathbb{R}^{N_y \times N_u}, \eta_n \sim N(0, R), R \in \mathbb{R}^{N_y \times N_y}
観測
u_n = \Psi(u_{n-1})
観測
u_1
y_1
u_2
y_2
t_1
t_2
t_3
...
\tau
\in \mathbb{R}^{N_y}
\in \mathbb{R}^{N_y}
\Psi
：観測時間間隔
(N_y \le N_u)
N_y
次元観測
観測行列
観測ノイズ
対称正定値
※ 連続時間観測の設定もあるが考えない．
既知
既知
準備：時系列状態推定
\Psi
...
u_1
u_2
u_3
u_0
y_1
y_2
y_3
\Psi
...
v_1
v_2
v_3
v_0
\Psi
\Psi
\Psi
\Psi
\Psi
\Psi
真値
観測値
推定値
from
Y_n = \{y_i \mid i \le n\}
問題
u_n
Estimate
n \in \mathbb{N},
known:
\Psi,
H,
観測ノイズの分布
時刻 までの観測のみ
n
\mathbb{P}^{u_n}({}\cdot{} | Y_n) \approx \frac{1}{m} \sum_{k=1}^m \delta_{v^{(k)}_n}
アプローチ
条件付き分布を近似．
典型的なものを紹介
目次：EnKF
観測ノイズ
「現実」
観測値
y_n = H u_n + \eta_n
(u_n)_n
✓
EnKF (2次モーメントまで考慮したアルゴリズム)
✓
観測
モデル
カオス
生成
u_n = \Psi(u_{n-1})
推定誤差
推定値
(v_n)_n
データ同化
t
y_1
y_2
t_1
t_2
t_3
\tau
t_0
v_0^{(1)}
v_0^{(m)}
v_0^{(2)}
\vdots
Ensemble Kalman filter (EnKF)
\mathbb{P}^{u_n}({}\cdot{} | Y_n) \approx \frac{1}{m} \sum_{k=1}^m \delta_{v^{(k)}_n}({}\cdot{})
に対して，条件付き分布を近似．
m \in \mathbb{N}
アンサンブル数
V_n = [v^{(k)}_n]_{k=1}^m
の時間発展を計算．
各
n \in \mathbb{N}
で以下の2ステップを行い
解析アンサンブル
\mathbb{P}^{u_n}({}\cdot{} | Y_n)
v^{(1)}_n,\dots,v^{(m)}_n
\mathbb{R}^{N_u}
(I)予測
\Psi
\widehat{v}_1^{(1)}
\widehat{V}_n = [\widehat{v}^{(k)}_n]_{k=1}^m
(予測アンサンブルは中間変数)
アンサンブルカルマンフィルタ
(II)解析
v_1^{(1)}
(観測値で予測を修正)
→ ベイズの公式で平均・共分散を考慮
→ 予測共分散 が重要！
詳細は割愛
\widehat{P}_n = \operatorname{Cov}_m(\widehat{V}_n)
...
(I) & (II)を繰り返す
EnKFの課題と数値テクニック
Key 予測の不確実性(ばらつき)を少ないアンサンブルで推定
\widehat{P}_n = \operatorname{Cov}_m(\widehat{V}_n)
: アンサンブル数
が小さい → 予測の不確実性を過小評価
m
観測を用いた
補正量に関わる
m
\widehat{v}_1^{(1)}
\widehat{v}_1^{(3)}
\widehat{v}_1^{(2)}
\Psi
課題
「本来」
\widehat{P}_n
予測共分散
\widehat{P}_n \rightarrow \widehat{P}_n + \alpha^2 I
\widehat{P}_n \rightarrow \alpha^2 \widehat{P}_n
\alpha
これを是正する数値テクニック
→ 共分散インフレーション
or
：インフレーションパラメータ
要チューニング
目次：EnKFの誤差解析
観測ノイズ
モデル
「現実」
観測値
データ同化
推定値
推定誤差
カオス
生成
y_n = H u_n + \eta_n
u_n = \Psi(u_{n-1})
(u_n)_n
(v_n)_n
✓EnKF + インフレーション
評価
(これから)
✓
✓
観測
主な仮定
N_y = N_x, H = I_{N_x}, \xi \sim \mathcal{N}(0, r^2 I_{N_x})
仮定
"全観測"
Strong!
\exist \rho > 0 \text{ s.t. } \forall x_0 \in B(\rho), \forall t > 0, x(t ; x_0) \in B(\rho).
\exist \beta > 0 \text{ s.t. } \forall x \in B(\rho), \forall x' \in \mathbb{R}^{N_x},
\langle F(x) - F(x'), x - x' \rangle \le \beta | x - x'|^2.
\exist \beta > 0 \text{ s.t. } \forall x, x' \in B(\rho), |F(x) - F(x')| \le \beta | x - x'|.
仮定
仮定
仮定
\forall x_0 \in \R^{N_x}, \dot{x}(t) = F(x(t))
Reasonable
(B(\rho) = \{x \in \R^{N_x} \mid |x| \le \rho \})
"one-sided Lipschitz"
"Lipschitz"
"有界なダイナミクス"
が一意な解をもち，
→ 散逸力学系
EnKFの数学解析の現状
-
Consistency (Mandel+2011, Kwiatkowski+2015)
-
Sampling errors (Al-Ghattas+2024)
-
Stability (Tong+2016a,b)
-
Filter accuracy (全観測 )
-
PO法 + 加法的inflation (Kelly+2014)
-
ESRF + 乗法的inflation (T.+2024, T. 2025)
-
H = I_{N_u}
How EnKF approximate KF?
EnKFの各実装が
真の軌道を「追跡」
できるか？
(\mathcal{F}: \text{ linear }, m \rightarrow \infty)
推定誤差
\le
定数 × 観測ノイズの分散
^2
→ 数学解析からの帰結：
インフレーション を大きくとると誤差評価ができる
\alpha
→ アルゴリズムの性能評価としては不十分．．．
目次：数値結果
観測ノイズ
モデル
「現実」
観測値
データ同化
推定値
推定誤差
カオス
生成
y_n = H u_n + \eta_n
u_n = \Psi(u_{n-1})
(u_n)_n
(v_n)_n
✓EnKF + インフレーション
✓理論評価
✓
✓
→ 数値検証（これから）
観測
数値検証の枠組み
Observing System Simulation Experiment (OSSE)
まず，データ同化の有効性を検証する標準的な枠組み
を紹介．
仮想的な真の状態を作って状態推定精度を評価．
双子実験とも呼ばれる．
数値検証の枠組み
Observing System Simulation Experiment (OSSE)
t
t_1
t_2
t_3
\tau
u_1
u_2
u_3
(1) 真の時系列を 生成
u_n
\mathbb{R}^{N_u}
数値検証の枠組み
Observing System Simulation Experiment (OSSE)
t
t_1
t_2
t_3
\tau
u_1
u_2
u_3
(2) ノイズを足して観測値 を生成
y_n
y_1
y_2
y_3
(1) 真の時系列を 生成
u_n
\mathbb{R}^{N_u}
数値検証の枠組み
Observing System Simulation Experiment (OSSE)
t
t_1
t_2
t_3
\tau
v_n
(3) 観測値 を同化し解析値（推定値） を計算
y_n
v_1
v_2
v_3
y_1
y_2
y_3
DA algorithm
(2) ノイズを足して観測値 を生成
y_n
(1) 真の時系列を 生成
u_n
\mathbb{R}^{N_u}
数値検証の枠組み
Observing System Simulation Experiment (OSSE)
t
t_1
t_2
t_3
\tau
\mathbb{R}^{N_u}
v_1
v_2
v_3
(4) 真値 と解析値 の差 を計算
u_n
v_n
e_1
e_2
e_3
u_1
u_2
u_3
v_n
(3) 観測値 を同化し解析値（推定値） を計算
y_n
(2) ノイズを足して観測値 を生成
y_n
(1) 真の時系列を 生成
u_n
e_n
数値例：Lorenz 96モデル
\frac{du^i}{dt} = (u^{i+1} - u^{i-2}) u^{i-1} - u^i + F,
Lorenz 96 (L96)
N_u \ge 4, \bm{u} = (u^i)_{i=1}^{N_u} \in \mathbb{R}^{N_u}, F \in \R,
非線形・エネルギー保存
線形・散逸
外力
地球の等緯度常に分布する物理量のカオスな変動を模した現象論的モデル．
(Lorenz1996)(Lorenz+1998)
u
(i = 1, \dots, N_u)
u^{0} = u^{N_u}, u^{-1} = u^{N_u - 1}, u^{N_u+1} = u^1.
※ 実数の絶対値とベクトルのユークリッドノルムの両方に
|\cdot|
を用いる．
気象データ同化でよく用いられるトイモデル
数値例：Lorenz 96モデル
時空間プロット
N_u = 60, F = 8.0, dt = 0.01
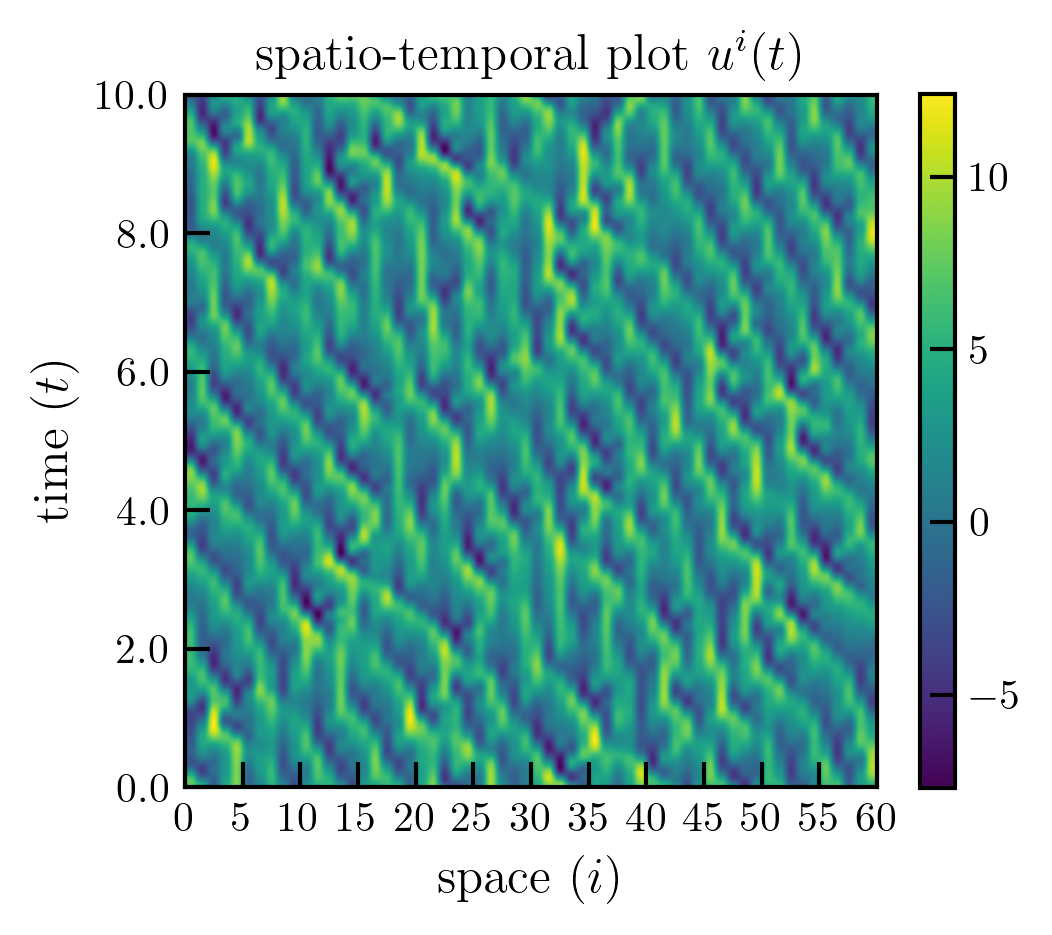
数値例: Lorenz 96 + EnKF
OSSE: EnKFをLorenz 96モデルに適用
N_u = 40, m = N_u+1 = 41, r = 1.0, \alpha = 1.0, 1.1, 5.0.
n
\le N_u r^2
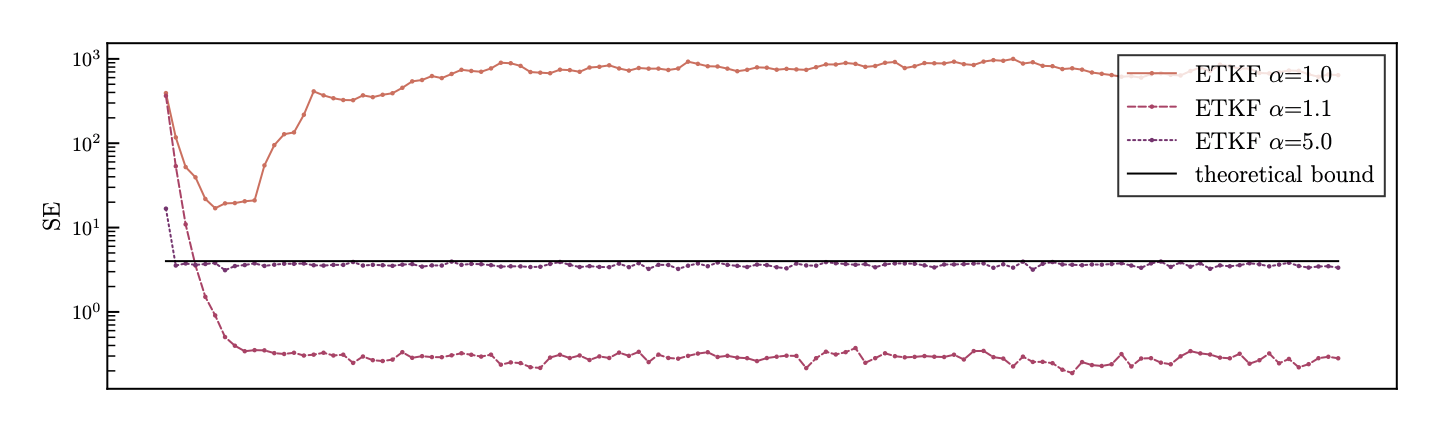
理論からの誤差評価
→ theoretical bound（観測ノイズの分散）
強インフレーション
弱インフレーション
インフレーションなし
推定誤差（SE）
乗法的インフレーション
図：状態推定誤差の時系列
(T.+2024) K. T. & T. Sakajo, SIAM/ASA Journal on Uncertainty Quantification, 12(4), 1315–1335.
考察：理論と応用のギャップ
誤差
観測ノイズ
のレベル
\alpha
紹介した理論は
この状況を解析
インフレーションパラメータと誤差の関係について
（現状の理解）
応用上は
この辺りが重要
インフレーションパラメータ
数値例: Lorenz 96 + EnKF
部分観測（例：観測次元が半分）でも推定可能
N_u = 40, N_y=20, m = 25, r = 1.0, \alpha = 1.0, 1.2
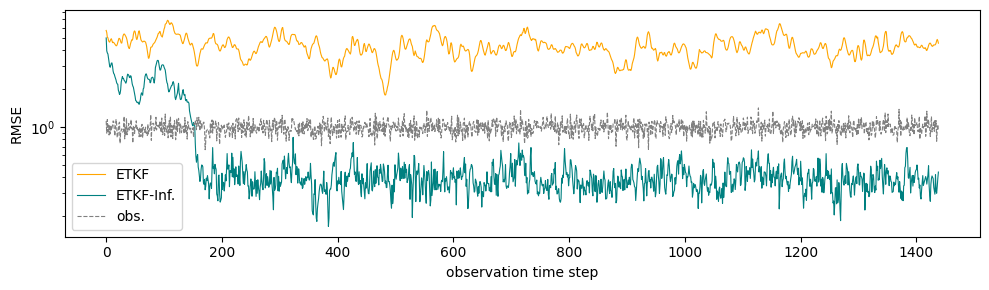
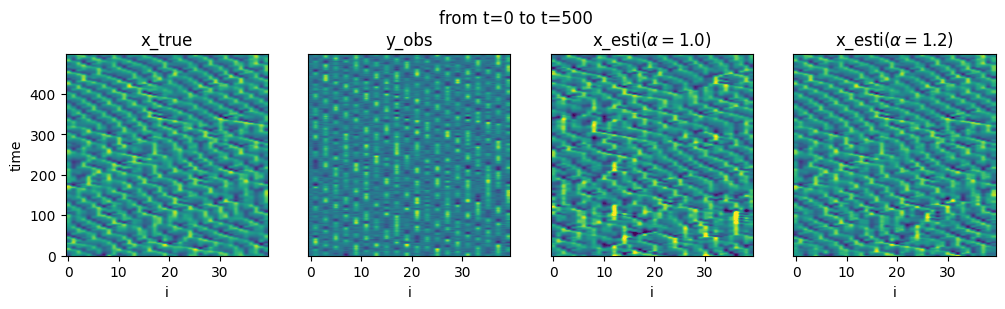
失敗
成功
まとめ
問題
カオス力学系の時系列状態推定問題について
データ同化アプローチを紹介．
結果
データ同化アルゴリズムの誤差評価を紹介．
数値計算から理論と応用のギャップも見つかった．
この理論解析では精度を改善できない．「安全性」を保証．
観測と同オーダーの精度評価
応用・展開
部分観測データで「安全性」を保証できると応用先が多い．
例：限られた観測地点で気象状態を推定する．
（その他：海洋，室温，感染症，交通流．．．）
まとめ
本講演に関連する論文
(T.+2024) K. T. & T. Sakajo, SIAM/ASA Journal on Uncertainty Quantification, 12(4), 1315–1335.
(T. 2025) K. T., Error Analysis of the Ensemble Square Root Filter for Dissipative Dynamical Systems, PhD Thesis, Kyoto University, 2025.
部分観測についての結果
(T. 2025) K. T., Error analysis of the projected PO method with additive inflation for the partially observed Lorenz 96 model, arXiv preprint.
個人サイト ↓
参考文献
- (T.+2024) K. T. & T. Sakajo, SIAM/ASA Journal on Uncertainty Quantification, 12(4), 1315–1335.
- (T. 2025) Kota Takeda, Error Analysis of the Ensemble Square Root Filter for Dissipative Dynamical Systems, PhD Thesis, Kyoto University, 2025.
- (Kelly+2014) D. T. B. Kelly, K. J. H. Law, and A. M. Stuart (2014), Well-posedness and accuracy of the ensemble Kalman filter in discrete and continuous time, Nonlinearity, 27, pp. 2579–260.
- (Al-Ghattas+2024) O. Al-Ghattas and D. Sanz-Alonso (2024), Non-asymptotic analysis of ensemble Kalman updates: Effective dimension and localization, Information and Inference: A Journal of the IMA, 13.
- (Tong+2016a) X. T. Tong, A. J. Majda, and D. Kelly (2016), Nonlinear stability and ergodicity of ensemble based Kalman filters, Nonlinearity, 29, pp. 657–691.
- (Tong+2016b) X. T. Tong, A. J. Majda, and D. Kelly (2016), Nonlinear stability of the ensemble Kalman filter with adaptive covariance inflation, Comm. Math. Sci., 14, pp. 1283–1313.
- (Kwiatkowski+2015) E. Kwiatkowski and J. Mandel (2015), Convergence of the square root ensemble Kalman filter in the large ensemble limit, Siam-Asa J. Uncertain. Quantif., 3, pp. 1–17.
- (Mandel+2011) J. Mandel, L. Cobb, and J. D. Beezley (2011), On the convergence of the ensemble Kalman filter, Appl.739 Math., 56, pp. 533–541.
参考文献
-
(de Wiljes+2018) J. de Wiljes, S. Reich, and W. Stannat (2018), Long-Time Stability and Accuracy of the Ensemble Kalman-Bucy Filter for Fully Observed Processes and Small Measurement Noise, Siam J. Appl. Dyn. Syst., 17, pp. 1152–1181.
-
(Burgers+1998) G. Burgers, P. J. van Leeuwen, and G. Evensen (1998), Analysis Scheme in the Ensemble Kalman Filter, Mon. Weather Rev., 126, 1719–1724.
-
(Bishop+2001) C. H. Bishop, B. J. Etherton, and S. J. Majumdar (2001), Adaptive Sampling with the Ensemble Transform Kalman Filter. Part I: Theoretical Aspects, Mon. Weather Rev., 129, 420–436.
-
(Anderson 2001) J. L. Anderson (2001), An Ensemble Adjustment Kalman Filter for Data Assimilation, Mon. Weather Rev., 129, 2884–2903.
-
(Dieci+1999) L. Dieci and T. Eirola (1999), On smooth decompositions of matrices, Siam J. Matrix Anal. Appl., 20, pp. 800–819.
-
(Reich+2015) S. Reich and C. Cotter (2015), Probabilistic Forecasting and Bayesian Data Assimilation, Cambridge University Press, Cambridge.
-
(Law+2015) K. J. H. Law, A. M. Stuart, and K. C. Zygalakis (2015), Data Assimilation: A Mathematical Introduction, Springer.
⾮線形カオス⼒学系の時系列状態推定と誤差解析
By kotatakeda
⾮線形カオス⼒学系の時系列状態推定と誤差解析
2025度統計関連学会連合大会 2025/9/9https://pub.confit.atlas.jp/ja/event/jfssa2025/session/3D10-13
