ノイズを含む部分観測に対するEnsemble Kalman Filterの誤差解析
2024年度応用数学合同研究集会 2024年12月5日@龍谷大学
The first author is supported by RIKEN Junior Research Associate Program and JST SPRING JPMJSP2110.
The second author is supported by JST MIRAI JPMJMI22G1.
○竹田 航太，坂上 貴之
\dagger
\dagger
京都大学 理学研究科
\dagger
noisy
partial
イントロ：気象予報と観測
(a) 観測ノイズ：統計的な誤差が含まれる．
(b) 部分観測：全格子・全変数のデータが揃っていない．
(x,y,z)\mapsto(x,y)
ノイズ
部分観測
現実の大気から得られる観測データの特徴
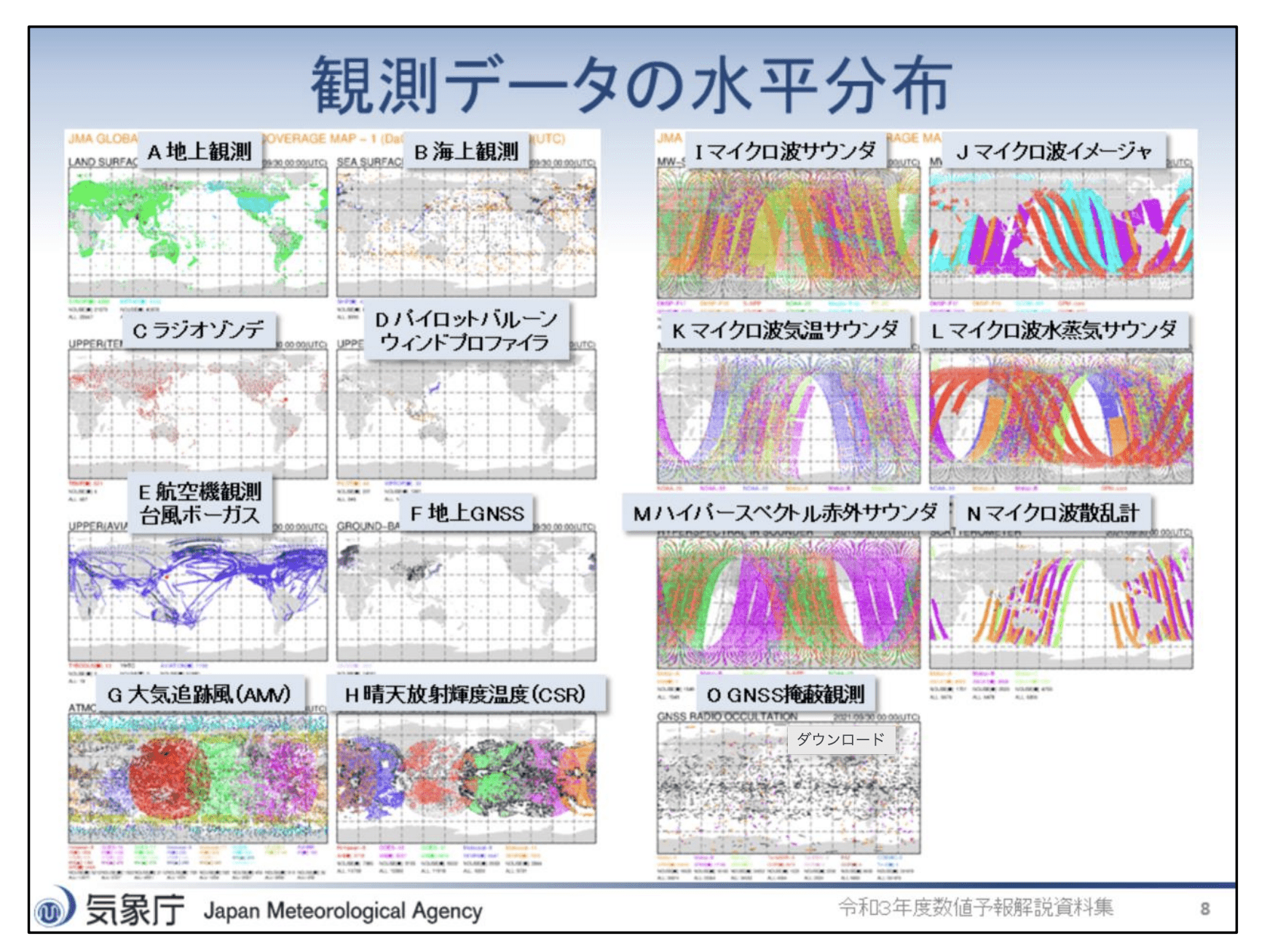
気象庁
→ 気象予報シミュレーションの初期値として
精度・解像度が不十分．
イントロ：データ同化
(a) 観測ノイズ
(b) 部分観測
「現実」
観測値
y_n = H u_n + \eta_n
(a)
(b)
(u_n)_n
Lorenz 96
EnKF
ある観測行列
H
評価
観測
一般のモデルで
H = I
の場合の結果はある．
(Kelly+2014, T.+2024)
モデル
カオス
生成
u_n = \Psi(u_{n-1})
推定誤差
推定値
(v_n)_n
データ同化
高精度
高解像度
準備：モデル（一般）
\frac{d u}{dt} = \mathcal{F}(u)
(\mathcal{F}: \R^{N_u} \rightarrow \R^{N_u}, u(0) = u_0 \in \R^{N_u})
\Psi_t (u_0) = u(t; u_0)
モデル
半群
\R^{N_u} (N_u \in \mathbb{N})
生成
(\Psi_t : \R^{N_u} \rightarrow \R^{N_u}, t \ge 0)
: 状態空間
モデル：既知，初期値：未知
t
真の解
未知
準備：Lorenz 96方程式
\frac{du^i}{dt} = (u^{i+1} - u^{i-2}) u^{i-1} - u^i + F,
Lorenz 96 (L96)
N_u \ge 4, \bm{u} = (u^i)_{i=1}^{N_u} \in \mathbb{R}^{N_u}, F \in \R,
非線形・エネルギー保存
線形・散逸
外力
地球の等緯度常に分布する物理量のカオスな変動を模した現象論的モデル．
(Lorenz1996)(Lorenz+1998)
u
(1)
(i = 1, \dots, N_u)
u^{0} = u^{N_u}, u^{-1} = u^{N_u - 1}, u^{N_u+1} = u^1.
※ 実数の絶対値とベクトルのユークリッドノルムの両方に
|\cdot|
を用いる．
補題1
F \in \R, u_0 \in \R^{N_u}
任意の
について，(1) の一意な解が存在する．
さらに，
\rho = \sqrt{2 N_u} |F|
に対して，
B(\rho) = \{v \in \mathbb{R}^{\Nu} \mid |v| \le \rho\}
は
次を満たす：
u_0 \in B(\rho) \Rightarrow u(t; u_0) \in B(\rho).
準備：観測（一般）
離散時間モデル
\mathbb{R}^{N_u}
\Psi = \Psi_\tau, \tau > 0
t
y_n = H u_n + \eta_n, \quad n \in \mathbb{N}.
H \in \mathbb{R}^{N_y \times N_u}, \eta_n \sim N(0, R), R \in \mathbb{R}^{N_y \times N_y}
観測
u_n = \Psi(u_{n-1})
観測
u_1
y_1
u_2
y_2
t_1
t_2
t_3
...
\tau
\in \mathbb{R}^{N_y}
\in \mathbb{R}^{N_y}
\Psi
：観測時間間隔
(N_y \le N_u)
N_y
次元観測
観測行列
観測ノイズ
準備：L96の部分観測
Lorenz 96方程式に対して，以下の部分観測を考える．
N_u = 3N
(\phi_i)_{i=1}^{N_u} \subset \mathbb{R}^{N_u}
イラスト
○
○
×
○
○
×
○
○
×
○
○
×
○: 観測
×: 観測しない
u^1
u^2
u^3
u \in \mathbb{R}^{3N}
N_u = 3N, N_y = 2N
N \in \mathbb{N}
H = [\phi_1, \phi_2, \phi_4, \phi_5, \phi_7, \dots]^\top \in \mathbb{R}^{N_y \times N_u}.
に対し
とする．
ただし，
は標準基底である．
← Key 1
(12)
H = [\phi_1, \phi_2, \phi_4, \phi_5, \phi_7, \dots]^\top
準備：時系列状態推定
\mathbb{R}^{N_u}
t
y_1
y_2
t_1
t_2
t_3
...
\tau
y_2
y_3
u_1
u_2
u_3
\Psi
\Psi
given
Y_n = \{y_i \mid i \le n\}
問題
u_n
Estimate
n \in \mathbb{N},
known:
\Psi,
H,
観測ノイズの分布
\mathbb{P}^{u_n}({}\cdot{} | Y_n) \approx \frac{1}{m} \sum_{k=1}^m \delta_{v^{(k)}_n}
アプローチ
条件付き分布を近似．
Ensemble Kalman filter (EnKF)
\mathbb{P}^{u_n}({}\cdot{} | Y_n) \approx \frac{1}{m} \sum_{k=1}^m \delta_{v^{(k)}_n}({}\cdot{})
に対して，条件付き分布を近似．
m \in \mathbb{N}
アンサンブル数
V_n = [v^{(k)}_n]_{k=1}^m
の時間発展を計算．
各
n \in \mathbb{N}
で以下の2ステップを行い
アンサンブル
\mathbb{P}^{u_n}({}\cdot{} | Y_n)
v^{(1)}_n,\dots,v^{(m)}_n
\widehat{v}^{(k)}_n = \Psi(v^{(k)}_{n-1}), \quad k = 1, \dots, m.
：各メンバーをモデルで時間発展．
(I) 予測
V_{n-1}
\widehat{V}_n = [\hat{v}^{(k)}_n]_{k=1}^m
予測アンサンブル
\widehat{V}_n
\rightarrow
(Burgers+1998)
\widehat{V}_n
V_{n-1}
V_n
y_n
(I)
(II)
y^{(k)}_n = y_n + \eta_n^{(k)}, \quad \eta_n^{(k)} \sim N(0, R), \quad k = 1, \dots, m.
\widehat{V}_n
v_n^{(k)} = (I - K_n H) \widehat{v}_n^{(k)} + K_n y_n^{(k)}, \quad k = 1, \dots, m.
K_n = \widehat{P}_n H^\top (H \widehat{P}_n H^\top + R)^{-1}, \widehat{P}_n = \operatorname{Cov}_m(\widehat{V}_n).
(\bigstar)
：まず，観測値を複製する．
次に予測値と観測値の重みつき平均を取る．
ただし，
(II) 解析
予測誤差共分散をサンプル共分散で近似
V_n
y_n
\rightarrow
,
EnKFの解釈
v^{(k)}_n = (I - K_n H) \widehat{v}^{(k)}_n + K_n y^{(k)}_n.
(\bigstar)
解析値 は予測値 と観測値 の重み付き平均．
v^{(k)}_n
\widehat{v}^{(k)}_n
y^{(k)}_n
R
: 観測の不確実性．既知．
\widehat{P}_n
: 予測の不確実性．アンサンブルで近似→
\operatorname{Cov}_m(\widehat{V}_n)
K_n = \widehat{P}_n H^\top (H \widehat{P}_n H^\top + R)^{-1}
重み
は以下の「比」で決まる．
\widehat{P}_n = \widehat{p}_n^2, R = r^2, H = 1
イメージ（スカラーの場合）
とする．
v^{(k)}_n = \frac{r^2}{r^2 + \widehat{p}_n^2} \widehat{v}^{(k)}_n + \frac{\widehat{p}_n^2}{r^2 + \widehat{p}_n^2} y^{(k)}_n
(\bigstar)
= \frac{1}{1 + \widehat{p}_n^2/r^2} \widehat{v}^{(k)}_n + \frac{\widehat{p}_n^2/r^2}{1 + \widehat{p}_n^2/r^2} y^{(k)}_n.
共分散インフレーション
(I) 予測 → → (II) 解析 → ...
アンサンブル数 が少ない時に状態推定を安定させるため，
(II)解析ステップの前に共分散行列を修正．
インフレーション
(\alpha \ge 0)
\widehat{P}_n \rightarrow \widehat{P}^\alpha_n = \widehat{P}_n + \alpha^2 I_{N_u}.
加法的インフレーション
既存の方法
→ 予測の不確実性を強制的に増大
射影加法的インフレーション
\widehat{P}_n \rightarrow \widehat{P}^\alpha_n = H^\top H (\widehat{P}_n + \alpha^2 I_{N_u}) H^\top H .
提案
(\alpha \ge 0)
直交射影行列
m
共分散インフレーションの背景
課題: アンサンブル数少ない時，誤差共分散行列が退化する．
(I) 予測 → → (II) 解析 → ...
m \le N_u \Rightarrow \operatorname{rank} \widehat{P}_n \le m-1 < N_u
解決策: (II)解析ステップの前に共分散行列を修正
\left(\widehat{P}_n = \frac{1}{m-1} \sum_{k=1}^m (\widehat{v}^{(k)}_n -\overline{\widehat{v}}_n) (\widehat{v}^{(k)}_n -\overline{\widehat{v}}_n)^\top \right)
インフレーション
(\alpha \ge 0)
\widehat{P}_n \rightarrow \widehat{P}^\alpha_n = \widehat{P}_n + \alpha^2 I_{N_u}.
加法的インフレーション
既存の方法
→ 行列のランクが回復
射影加法的インフレーション
\widehat{P}_n \rightarrow \widehat{P}^\alpha_n = H^\top H (\widehat{P}_n + \alpha^2 I_{N_u}) H^\top H .
提案
(\alpha \ge 0)
直交射影行列
データ同化
(a) 観測ノイズ
(b) 部分観測
モデル
「現実」
観測値
データ同化
推定値
推定誤差
カオス
生成
y_n = H u_n + \eta_n
u_n = \Psi(u_{n-1})
(a)
(b)
(u_n)_n
(v_n)_n
✓Lorenz 96
✓EnKF
✓ある観測行列
H
評価
(これから)
観測
一般のモデルで
H = I
の場合の結果はある．
(Kelly+2014, T.+2024)
主結果：誤差評価
各メンバーの誤差を
\delta^{(k)}_n = v_n^{(k)} - u_n \ (k=1, \dots, m)
とおき，
\|v\| = \sqrt{|v|^2 + |Hv|^2}
ノルム
を用いて評価する．
(r > 0)
定理1
\limsup_{n \rightarrow \infty} \mathbb{E}[\|\delta^{(k)}_n \|^2] \le \frac{4 N_y}{1-\theta}r^2
(k = 1, \dots, m).
v_n^{(k)} \in B(\rho) \quad (n \in \N, k = 1, \dots, m).
L96方程式 (1)，観測行列 (12)及び観測誤差共分散
R = r^2 I_{N_y}
に対し，EnKF及び射影加法的インフレーションを適用する．
任意の観測時間間隔
\tau > 0
アンサンブル数
m \in \mathbb{N}
インフレーションパラメータ
\alpha > 0
に対して，
以下を仮定する．
このとき，十分小さい
\tau > 0
と十分大きい
\alpha > 0
に対し，
\theta \in (0, 1)
が存在して，以下が成立．
予測誤差を抑える
予測の重みを小さく
観測ノイズの分散
主結果：誤差評価
定理1の詳細な評価
\mathbb{E}[\| \delta^{(k)}_n \|^2] \le \theta^n \mathbb{E}[\| \delta^{(k)}_0 \|^2] + \frac{4 N_y r^2 ( 1 - \theta^n)}{1-\theta},
(k = 1, \dots, m).
各メンバーの誤差を
\delta^{(k)}_n = v_n^{(k)} - u_n
とおき，
\|v\| = \sqrt{|v|^2 + |Hu|^2}
ノルム
を用いて評価する．
十分小さい
\tau > 0
と十分大きい
\alpha > 0
に対し，
\theta \in (0, 1)
が存在して，以下が成立．
exponential decay
initial error
定理1の仮定の下で
主結果：証明の流れ
定理1
射影インフレーション
EnKF
部分観測 (12)
Lorenz 96方程式
誤差拡大(補題2)
(I)予測ステップ
誤差縮小(補題3)
(II)解析ステップ
Key1
Key2
誤差のノルム
t
．．．
誤差拡大(補題2)
誤差縮小(補題3)
(I)予測
(II)解析
主結果：予測ステップでの誤差拡大
L96方程式に対して，良い部分観測 (12)を考えると以下の誤差拡大評価を得る．
補題2
観測行列 (12)を考える．
u_0, v_0 \in B(\rho), t \ge 0
について，
\delta(t) = \Psi_t(v_0) - \Psi_t(u_0)
とおく．このとき，
t \ge 0
で以下が成立．
|H \delta(t)|^2 \le A_1(t) |\delta(0)|^2 + |H \delta(0)|^2,
|\delta(t)|^2 \le B_1(t) |\delta(0)|^2 + B_2(t) |H \delta(0)|^2.
は予稿を参照．
A_1(\tau), B_1(\tau), B_2(\tau)
(15)
(16)
注意：
A_1(\tau), B_1(\tau), B_2(\tau) < 1
を十分小さくと取ると
t = \tau > 0
とできる．
※ 補題2の証明 → Gronwallの不等式に基づく．
(20)
Key1
主結果：解析ステップでの誤差縮小
EnKFに射影加法的インフレーションを適用すると観測成分での誤差縮小を得る．
\Theta = \Theta(\alpha)
注意：
は
\alpha
を大きく取ることで，
\Theta(\alpha) \searrow 0 \quad (\alpha \rightarrow \infty)
いくらでも小さくできる．
補題3
定理1の仮定の下，
\Theta = \left(\frac{r^2}{r^2 + \alpha^2}\right)^2
とおく．
について，以下が成立．
k = 1, \dots, m
このとき，
\mathbb{E}[|H\delta^{(k)}_n|^2] \le \Theta \mathbb{E}[|H\widehat{\delta}^{(k)}_{n-1}|^2] + 2N_y r^2,
\mathbb{E}[|\delta^{(k)}_n|^2] \le \mathbb{E}[|\widehat{\delta}^{(k)}_{n-1}|^2] + 2N_y r^2.
(23)
(24)
(25)
Key2
予測誤差
観測誤差
縮小
※ 作用素ノルムの評価で射影が重要．
主結果：解析ステップでの誤差縮小
補題3の証明
\mathbb{E}[|H\delta^{(k)}_n|^2] \le \Theta \mathbb{E}[|H\widehat{\delta}^{(k)}_{n-1}|^2] + 2N_y r^2,
\mathbb{E}[|\delta^{(k)}_n|^2] \le \mathbb{E}[|\widehat{\delta}^{(k)}_{n-1}|^2] + 2N_y r^2.
(23)
(24)
(23)の右辺第１項，(24)右辺第2項の評価にそれぞれ
|(I_{N_y} + HG_n)^{-1}|_{op} = \Theta^{1/2},
|(I_{N_u} + G_n)^{-1}G_n|_{op} \le 1
という評価を用いる．
(27)
(26)
G_n = r^{-2}\widehat{P}_n^{\alpha} H^\top H
ただし，
である．
(目標)
誤差縮小
観測ノイズの影響
(27)では，
G_n
の対称半正定値性が重要．
→ インフレーション時の射影から従う．
(26)では，
G_n
の最小固有値が正であることが重要．
→ 加法的インフレーションから従う．
\lambda_{min}(G_n) = \lambda_{min}(r^{-2}H^\top H (\widehat{P}_n + \alpha^2 I) H^\top H) = r^{-2}\alpha^2 > 0
|\cdot|_{op}
は作用素ノルム．
主結果：証明の流れ
定理1
射影インフレーション
EnKF
部分観測 (12)
Lorenz 96方程式
誤差拡大(補題2)
誤差縮小(補題3)
誤差のノルム
t
．．．
誤差拡大(補題2)
でコントロール
誤差縮小(補題3)
でコントロール
\alpha
\tau
既存研究との比較
| (a) ＼ (b) | 全観測 | 部分観測 |
|---|---|---|
| ノイズなし | - | Synchronization [6, 7] |
| ノイズあり | EnKF [3, 4] | EnKF (本研究) |
(a) 観測ノイズ：統計的な誤差が含まれる．
(b) 部分観測：全格子・全変数のデータが揃っていない．
モデルは「一般」
[3] (Kelly+2014) [4] (T.+2024) [6] (Law+2016) [7] (Azouani+2014)
L96方程式, Navier-Stokes方程式 (NSE)
L96方程式
※ Synchronization
ノイズのない部分観測から時間漸近的に真の解を再構成
\mathcal{F} \circlearrowright u(t) \overset{H u(t)}{\rightarrow} v(t) \circlearrowleft \mathcal{F} \Rightarrow |u(t) - v(t)| \rightarrow 0 \ (t \rightarrow \infty)
観測の設定と誤差評価
予想
拡張
Synchronizationの既存結果からHを使う
Lorenz 63 (Hayden+2011), 2D-NSE (Aouzani+2014)
抽象論
散逸力学系 → 有限次元アトラクター，inertial manifold
→ 有限ランクの観測作用素 Hの存在
与えられた観測に対して時間大域評価が可能か判定することや，観測に対する制約のもとで最低ランクのものを見つけることは難しい
一方で，
(Hayden+2011)
数値結果: L96 (定理1の検証)
② add, projで挙動は変わらない．→ addでも誤差評価の可能性．
EnKFに2種類のインフレーションを3種類の で適用．
\alpha
加法的(add)，射影加法的(proj)
その他パラメータ：
N_u = 60, N_y = 40, \tau = 0.01, r=1, m=10.
① 誤差は
\alpha=0.0 > 2.0 > 0.5.
→ が大きければ良いわけではない．
\alpha
\alpha = 0.0
\alpha = 2.0
\alpha = 0.5
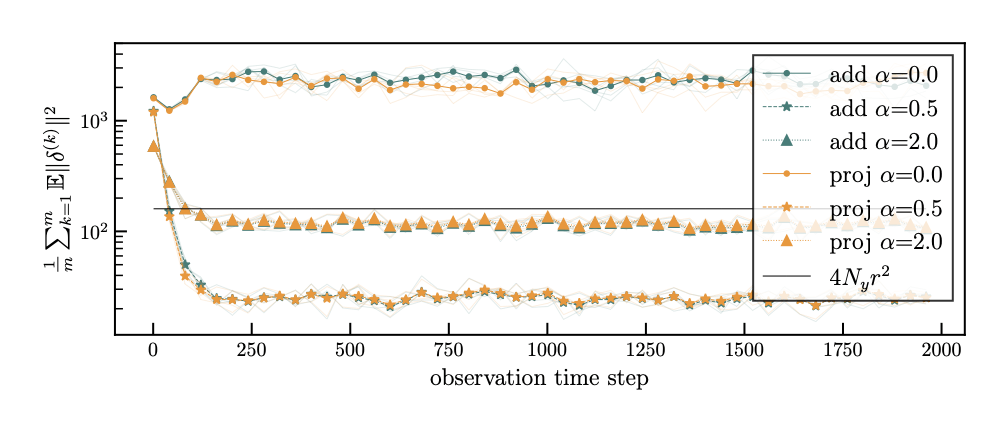
定理1の評価
観察
数値結果: Lorenz 63方程式
\left\{
\begin{array}{cc}
\dot{x} & = -\sigma x + \sigma y,\\
\dot{y} & = \varrho x - y - xz,\\
\dot{z} & = - bz + xy.
\end{array}
\right.
典型的なパラメータは
\sigma = 10, b = 8/3, \varrho = 28.
3変数の常微分方程式
まとめ
1. Synchronizationが成り立つような良い部分観測を取り，
予測誤差共分散を射影することで，
EnKFの時間大域的な誤差評価を得た．
2. NSEなど他の散逸力学系でも同様の方針で示せそう．
射影がない加法的インフレーションでも示せるかも．
近い将来
3. 超高次元の問題への応用上は，メモリ負荷の理由から
加法的インフレーションが非現実的
→ この場合はより精密な共分散行列の解析が必要．
さらにその先．．．
Key1: L96の部分観測 → 誤差拡大のコントロール
Key2: 射影加法的インフレーション → 行列の対称性
References
- (T.+2024) K. T. & T. Sakajo, SIAM/ASA Journal on Uncertainty Quantification, 12(4), 1315–1335.
- (T.) Kota Takeda, Error Analysis of the Ensemble Square Root Filter for Dissipative Dynamical Systems, PhD Thesis, Kyoto University, 2025.
- (Kelly+2014) D. T. B. Kelly, K. J. H. Law, and A. M. Stuart (2014), Well-posedness and accuracy of the ensemble Kalman filter in discrete and continuous time, Nonlinearity, 27, pp. 2579–260.
- (Al-Ghattas+2024) O. Al-Ghattas and D. Sanz-Alonso (2024), Non-asymptotic analysis of ensemble Kalman updates: Effective dimension and localization, Information and Inference: A Journal of the IMA, 13.
- (Tong+2016a) X. T. Tong, A. J. Majda, and D. Kelly (2016), Nonlinear stability and ergodicity of ensemble based Kalman filters, Nonlinearity, 29, pp. 657–691.
- (Tong+2016b) X. T. Tong, A. J. Majda, and D. Kelly (2016), Nonlinear stability of the ensemble Kalman filter with adaptive covariance inflation, Comm. Math. Sci., 14, pp. 1283–1313.
- (Kwiatkowski+2015) E. Kwiatkowski and J. Mandel (2015), Convergence of the square root ensemble Kalman filter in the large ensemble limit, Siam-Asa J. Uncertain. Quantif., 3, pp. 1–17.
- (Mandel+2011) J. Mandel, L. Cobb, and J. D. Beezley (2011), On the convergence of the ensemble Kalman filter, Appl.739 Math., 56, pp. 533–541.
References
-
(de Wiljes+2018) J. de Wiljes, S. Reich, and W. Stannat (2018), Long-Time Stability and Accuracy of the Ensemble Kalman-Bucy Filter for Fully Observed Processes and Small Measurement Noise, Siam J. Appl. Dyn. Syst., 17, pp. 1152–1181.
-
(Burgers+1998) G. Burgers, P. J. van Leeuwen, and G. Evensen (1998), Analysis Scheme in the Ensemble Kalman Filter, Mon. Weather Rev., 126, 1719–1724.
-
(Bishop+2001) C. H. Bishop, B. J. Etherton, and S. J. Majumdar (2001), Adaptive Sampling with the Ensemble Transform Kalman Filter. Part I: Theoretical Aspects, Mon. Weather Rev., 129, 420–436.
-
(Anderson 2001) J. L. Anderson (2001), An Ensemble Adjustment Kalman Filter for Data Assimilation, Mon. Weather Rev., 129, 2884–2903.
-
(Dieci+1999) L. Dieci and T. Eirola (1999), On smooth decompositions of matrices, Siam J. Matrix Anal. Appl., 20, pp. 800–819.
-
(Reich+2015) S. Reich and C. Cotter (2015), Probabilistic Forecasting and Bayesian Data Assimilation, Cambridge University Press, Cambridge.
-
(Law+2015) K. J. H. Law, A. M. Stuart, and K. C. Zygalakis (2015), Data Assimilation: A Mathematical Introduction, Springer.
References
-
(Law+2016) K. J. H. Law et al., Filter accuracy for the Lorenz 96 model: Fixed versus adaptive observation operators, Phys. Nonlinear Phenom., 325, 1–13.
-
(Azouani+2014) A. Azouani, E. Olson, and E. S. Titi, Continuous Data Assimilation Using General Interpolant Observables, J. Nonlinear Sci., 24, 277–304.
-
(Hayden+2011) K. Hayden, E. Olson, and E. S. Titi, Discrete data assimilation in the Lorenz and 2D Navier-Stokes equations, Phys. -Nonlinear Phenom., 240, pp. 1416– 1425.
ノイズを含む部分観測に対するEnsemble Kalman Filterの誤差解析
By kotatakeda
ノイズを含む部分観測に対するEnsemble Kalman Filterの誤差解析
2024年度応用数学合同研究集会「ノイズを含む部分観測に対するEnsemble Kalman Filterの誤差解析」, 龍谷大学, 12/5.
