Median Voter Theorem
Lecture 1 Part 2, Political Economics I
OSIPP, Osaka University
6 October, 2017
Masa Kudamatsu
What is Median Voter Theorem?
Elections induce politicians to propose
the policy favored by the median voter
Roughly speaking, the Theorem says:
The policy favored by the median voter
Example: the consumption tax rate in Japan
Survey of my undergrad class (9 students) last year
3%
5%
5%
5%
7%
7%
7%
7%
10%
Median
Basic Model
Known as the Downsian model of electoral competition
as it's first formalized by Downs (1957)
Here we follow the exposition by
Sections 3.2-3.3 of Persson and Tabellini (2000)
Players
Two candidates, each indexed by
P \in \{A, B\}
A continuum of citizens, each indexed by
i
Candidates' preference
If they win the election, ego rent
R
If they lose the election, the payoff is normalized to zero
Denote candidate P's probability of winning by
p_P
Then candidate P's expected utility is
p_P R
Candidates just want to be in office, not caring about policy
Often called office-seeking candidates
Candidate P chooses a policy to maximize
p_P R
Candidates' action
Candidate P proposes a policy
g_P \in \mathbb{R}
e.g.
Tax rate
Government expenditure on education
NOTE: We assume candidates can commit to the proposed policy
This assumption is crucial for the Median Voter Theorem
Citizens' preference
The farther away the policy is from citizen i's ideal,
the smaller his/her payoff from that policy
Citizens have a single-peaked preference over policy g
i.e.
An example single-peaked preference
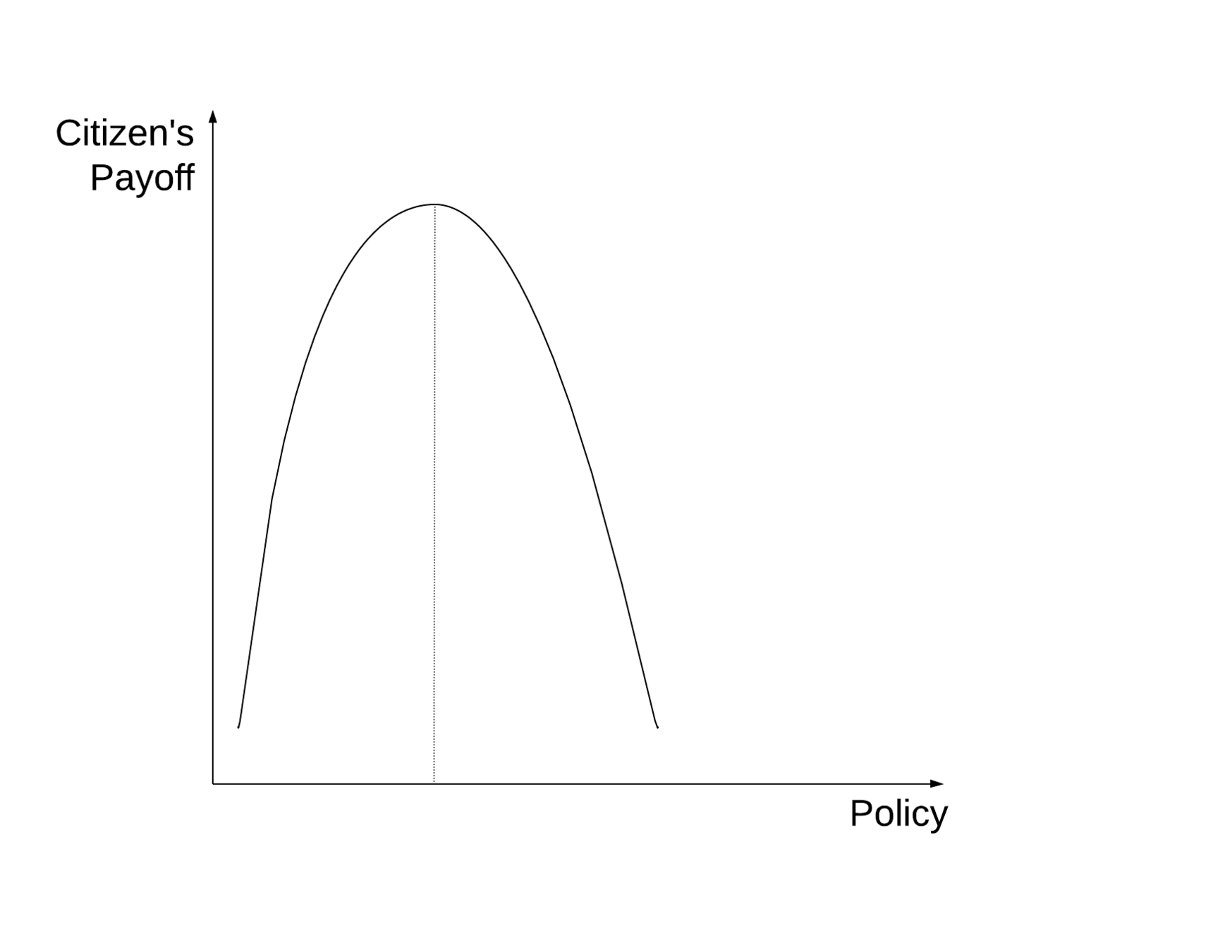
The farther away the policy is from the ideal
The lower the payoff
Citizens' preference (cont.)
W^i(g'') \leq W^i(g')
for any \(g'\) and \(g''\) such that
g'' \leq g' \leq g^i
or
g^i \leq g' \leq g''
Formally, denote citizen i's payoff function by
Citizen i's ideal policy is given by
g^i =\arg\max_g W^i(g)
W^i(g)
W^i(g)
represents a single-peaked preference if
W^i(g'') \leq W^i(g')
for
g^i \leq g' \leq g''
g^i
g'
g''
W^i(g'') \leq W^i(g')
for
g^i
g'
g''
g'' \leq g' \leq g^i
NOTE: we will see how far we can relax this assumption
for the Median Voter Theorem to hold
Citizens' preference
Different citizens have different ideal policies
g^i
Citizens' preference
g^i
g^k
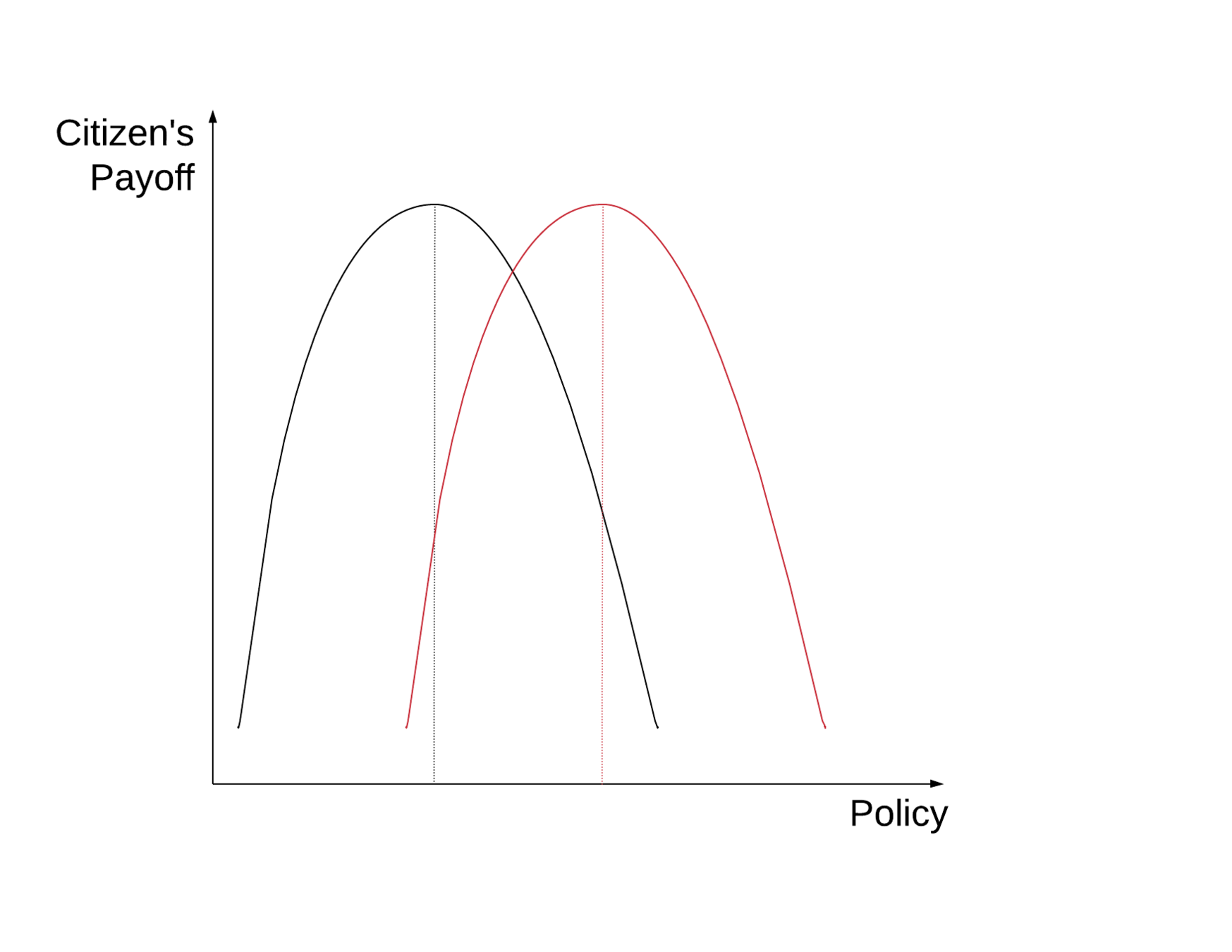
Different citizens have different ideal policies
Median Voter
Denote the median value of
g^i
by
g^M
Call the citizen whose ideal policy is
g^M
the median voter
indexed by
i=M
Citizens' action
Each citizen decides whether to vote for candidate A or B
NOTE: we assume no citizen abstains from voting
In Lecture 6, we discuss how we model voter turnout
Otherwise, we maintain this assumption throughout the course
(and also in most studies in political economics)
Timing of Events
Each citizen simultaneously decides whom to vote, candidate A or B
1
Each candidate simultaneously proposes policy
g_A, g_B
2
3
The candidate who obtains the majority implements the proposed policy. The payoff realizes.
Election Campaign
Election
Inauguration of a new government
Analysis
Subgame Perfect Nash Equilibrium
The model is an example of the extensive form game
Equilibrium concept: Subgame Perfect Nash Equilibrium
We can obtain the equilibrium by backward induction
See Chapters 7-8 of Tadelis (2013)
if this slide looks like Egyptian hieroglyphs
Backward induction
Timing of Events
Each citizen simultaneously decides whom to vote, candidate A or B
1
Each candidate simultaneously proposes policy
2
3
The candidate who obtains the majority implements the proposed policy. The payoff realizes.
Election Campaign
Election
Inauguration of a new government
Find the optimal behavior for the last player first
Citizen i's optimization
Vote for
W^i(g_A) > W^i(g_B)
A
if
B
<
Flip the coin
=
Vote for the candidate whose policy yields a higher payoff
To see which candidate obtains the majority of votes,
we can just consider the median voter's decision
g^i
g_A
g_B
Suppose candidates A and B propose the following policies
Since each citizen votes for the policy closer to their ideal...
Vote for B
\frac{g_A+g_B}{2}
Vote for A
To see which candidate obtains the majority of votes,
we can just consider the median voter's decision
g^i
g_A
g_B
If the median voter votes for B...
Vote for B
\frac{g_A+g_B}{2}
Vote for A
g^M
B gets the majority
More than 50% of votes
To see why the single-peaked preference matters...
W^M(g_A)>W^M(g_B)
Then all citizens with
g^i > g^M
also prefer to vote for A
Suppose
(1) Candidate A proposes a higher g:
g_A > g_B
(2) Median voter votes for A:
Then
g
g_A
g_B
g^M
by the single-peaked preference
g^i
So candidate A wins the majority by the definition of median
To see which candidate obtains the majority of votes,
we can just consider the median voter's decision
W^M(g_A) > W^M(g_B)
Then all citizens with
g^i < g^M
also prefer to vote for A
Suppose
(1) Candidate B proposes a higher g:
g_A < g_B
(2) Median voter votes for A:
Then
g
g_A
g_B
g^M
by the single-peaked preference
g^i
So candidate A wins the majority by the definition of median
To see which candidate obtains the majority of votes,
we can just consider the median voter's decision
W^M(g_A) < W^M(g_B)
Then all citizens with
g^i >g^M
also prefer to vote for B
Suppose
(1) Candidate B proposes a higher g:
g_A < g_B
(2) Median voter votes for B:
Then
g
g_A
g_B
g^M
by the single-peaked preference
g^i
So candidate B wins the majority by the definition of median
To see which candidate obtains the majority of votes,
we can just consider the median voter's decision
W^M(g_A) < W^M(g_B)
Then all citizens with
g^i < g^M
also prefer to vote for B
Suppose
(1) Candidate A proposes a higher g:
g_A > g_B
(2) Median voter votes for B:
Then
g
g_A
g_B
g^M
by the single-peaked preference
g^i
So candidate B wins the majority by the definition of median
Summing up the results so far
in terms of A's winning probability
(candidate A wins)
p_A = 1
if
p_A
W^M(g_A)>W^M(g_B)
p_A = 0
(candidate B wins)
if
<
p_A = \frac{1}{2}
if
=
Backward induction (cont.)
Timing of Events
Each citizen simultaneously decides whom to vote, candidate A or B
1
Each candidate simultaneously proposes policy
2
3
The candidate who obtains the majority implements the proposed policy. The payoff realizes.
Election Campaign
Election
Inauguration of a new government
Now find the optimal behavior of the first players
assuming they correctly predict the last players' behavior
Candidate A's optimization
To maximize
p_A
Propose
g_A
that is closer to
g_M
than
g_B
Candidate B's optimization
To maximize
1- p_A
Propose
g_B
that is closer to
g_M
than
g_A
Subgame Perfect Nash Equilirium
Both candidates propose the median voter's ideal policy
g_A^*=g_B^*=g^M
This is the prediction of the Median Voter Theorem
is sometimes called the Condorcet winner
g^M
A policy that defeats any other policy in a majority voting
Implications
Policy Convergence
Both candidates propose the same, centralist policy
Not too bad a prediction for Japan perhaps
In reality, however, there are situations of policy divergence
How to derive policy divergence as the equilibrium
has been a big research agenda in theoretical political economy
Robustness
of the basic model
Citizens' preference
The basic model imposes the single-peaked preference
This assumption can be relaxed to the single-crossing property
Formal definition of the single-crossing property
Denote citizens' preference over policy by
W(q, \alpha^i)
Policy (e.g. tax rate)
q \in \mathbb{R}
Preference type (e.g. income)
\alpha \in \mathbb{R}
The single-crossing property is satisfied if
q > q'
W(q,\alpha) \geq W(q',\alpha) \Rightarrow W(q,\alpha') \geq W(q',\alpha')
for
\alpha > \alpha'
and
q < q'
, or for
\alpha < \alpha'
and
Graphically, the single-crossing property holds if
\alpha
W(q,\alpha)-W(q',\alpha)
0
Or if
\alpha
W(q,\alpha)-W(q',\alpha)
0
See Example 1 (pp. 24-25) of Persson and Tabellini (2000)
for an example of the preference satisfying the single-crossing property but not single-peaked
Multi-dimensional policy
The basic model assumes one-dimensional policy space
For multi-dimensional policy space,
the Median Voter Theorem holds
if citizens' preference satisfies the following condition
(Grandmont 1978; see Section 2.2.2 of Persson and Tabellini 2000)
Citizens have intermediate preferences if their indirect utility function takes the form of
W(\mathbf{q}; \alpha^i) = J(\mathbf{q}) + K(\alpha^i)H(\mathbf{q})
where q is the policy vector,
\alpha^i
citizen i's type parameter,
K(\alpha^i)
monotonic in
\alpha^i
In words, the intermediate preference allows
multi-dimensional policy space to be collapsed
into one-dimensional space
Multi-dimensional policy (cont.)
e.g.
Expenditure on education
Expenditure on health
Unemployment insurance
If a citizen prefers a higher spending for one policy,
she also prefers a higher spending for the others
Multi-dimensional policy (cont.)
Otherwise, the Downsian model has no equilibrium.
The most important example: the division of a pie
To analyze such policy-making, two approaches are now used
Probabilistic Voting Model
Legislative Bargaining Model
(Lecture 3)
(Lecture 5)
Multi-dimensional policy (cont.)
Candidates' preference
In the basic model, candidates earn "ego rent" if elected
What if candidates share the same preference as citizens'?
Wittman (1977) and Calvert (1985)
consider such an extension of the Downsian model
See Section 5.1 of Persson and Tabellini (2000) for detail
They show the Median Voter Theorem still holds
Candidates' commitment to electoral promise
In the basic model, candidates announce the policy before election
But the winning candidate may want to change their mind
See Section 5.2 of Persson and Tabellini (2000) for detail
Citizens won't be fooled by electoral promises
Alesina (1988) drops the commitment assumption
They vote for the candidate whose bliss point is closer to theirs
Then the candidate whose bliss point is closer to the median will win
Candidates' commitment to electoral promise
If the candidate whose bliss point is closer to the median will win...
Why not a citizen whose bliss point is even closer to the median won't run for office?
We need to consider which citizens run for office
The citizen-candidate model
(Lecture 2)
Summary
We cannot use the Median Voter Theorem when
The policy issue is multi-dimensional (e.g. division of a pie)
Citizens' preference deviates from the single-crossing property
Candidates cannot commit to their electoral promise
Applications
Despite all these limitations...
the Median Voter Theorem has been applied to many contexts
for its simplicity
Guembel and Sussman (2009 Restud) for a theory of sovereign debt
Median voter may prefer repaying debt
even without any penalty for default
Bolton and Roland (1997 QJE) for the break-up of a nation
The level of taxation is chosen by the median voter
of the whole nation or of the break-away territory
Jaimovich and Rebelo (2017 JPE) for the impact of taxation on growth
Among many other applications,
the most influential is perhaps Meltzer and Richard (1981)
They argue that
the franchise extension increases the size of government
This paper gave birth to so many theories and empirical studies
See Acemoglu et al. (2016) for the latest literature review
We follow Sections 3.1-3.3 of Persson and Tabellini (2000)
to illustrate their model as an example of how to incorporate the Downsian model of elections into a model of the economy
A model of public finance
Demography
A continuum of citizens with population size normalized to 1
Each citizen type is indexed by
i
Preference
Citizen of type i has the preference over consumption & public good
c^i + H(g)
is a concave, increasing function
H(g)
where
A model of public finance (cont.)
Endowment
Citizen of type i is endowed with income
y^i
Income distribution is given by a c.d.f.
F(y^i)
Denote the median income as
y^m
F(y^m) = 1/2
i.e.
Empirically we observe
y^m < y \equiv E(y^i)
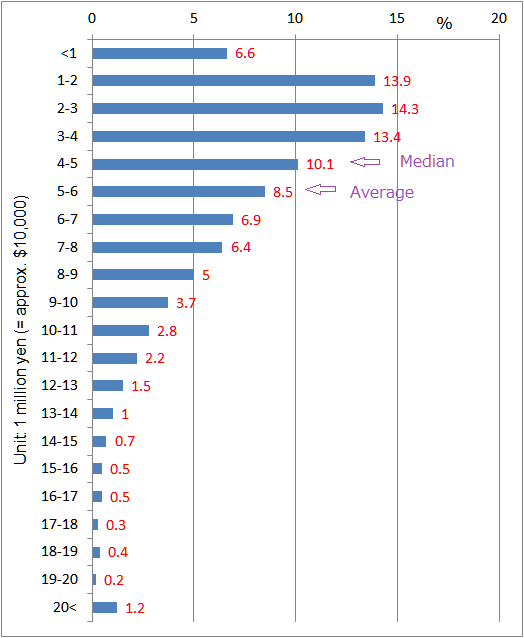
Japan's income distribution
in 2013
Source: Ministry of Health, Labour and Welfare
(国民生活基礎調査)
A model of public finance (cont.)
Government
Collect tax at a common rate of income
\tau
Produce public good by the technology
g = \int_i \tau y^i dF = \tau y
Citizen i's disposable income is equal to their consumption
c^i =(1-\tau)y^i
NOTE: Since the population size is 1,
GDP is the same as GDP per capita, both expressed as
y
There are two policy variables, tax and public good
A model of public finance (cont.)
Since the government budget is balanced
g = \tau y
choosing the level of public good provision gives the unique tax rate
So there is effectively one single policy
g
Let's rewrite citizens' payoff as a function of
g
Citizen i' payoff as a function of public good
\equiv W^i(g)
c^i + H(g) = (1-\tau)y^i + H(g)
=\frac{y(1-\tau) y^i}{y} + H(g)
=(y-g)\frac{y^i}{y} + H(g)
(by \(g=\tau y\))
Normative benchmark (First-best policy)
Social planner maximizes the sum of all citizens' payoffs
\int_iW^i(g)dF= \int_i \{(y-g)\frac{y_i}{y}+H(g)\}dF
=\frac{y-g}{y}\int_i y^idF+H(g)
=(y-g)\frac{y}{y}+H(g)
=W(g)
Social optimum is implicitly defined by
1=H_g(g^{FB})
Endogenize the policy
Suppose the level of public good provision g is chosen by the following political process (i.e. the Downsian model)
Each citizen simultaneously decides whom to vote, candidate A or B
1
Each of the two candidates simultaneously proposes policy
2
3
The candidate who obtains the majority implements the proposed policy. The payoff realizes.
Election Campaign
Election
Inauguration of a new government
Analysis
Check whether citizens' preference satisfies the single-crossing property.
If so, the Median Voter Theorem holds:
the median voter's ideal policy will be the equilibrium policy proposed by both candidates
Policy space is one-dimensional
Single-crossing property
Citizen's preference type can be expressed by
y^i
W^i(g)=(y-g)\frac{y^i}{y} + H(g)
We need to show
if \(g > g'\) and \( y^j > y^k \), or \(g < g'\) and \( y^j < y^k \)
W^j(g) \geq W^j(g') \Rightarrow W^k(g) \geq W^k(g')
Equilibrium policy
Payoff of citizens with median income
Since the Median Voter Theorem holds,
it's the median income earner's ideal policy
Maximizing this payoff w.r.t. g yields
W^m(g)=(y-g)\frac{y^m}{y} + H(g)
y^m/y=H_g(g^*)
Political distortion
y^m/y=H_g(g^*)
Equilibrium policy is given by
Compare this to the first-best policy
1=H_g(g^{FB})
Since
y^m < y
(empirically),
g^* > g^{FB}
we have the over-provision of public goods:
Impact of franchise extension
Now suppose
only citizens with income higher than can vote
\overline{y}
Suffrage used to be restricted by wealth in 19c Europe
In early 20c Japan
those paying more than 15 yen as taxes could vote
cf.
The Median Voter Theorem says
the median income earner among those franchised is decisive
Impact of franchise extension
Now suppose
only citizens with income higher than can vote
\overline{y}
Then the equilibrium policy is given by
\overline{y^m}/y=H_g(\overline{g^*})
where
\overline{y^m}
is the median income conditional on
y^i>\overline{y}
Empirical predictions
y^m/y=H_g(g^*)
Since
H_g(g)
g
y^m/y
g^*
\overline{y^m}/y=H_g(\overline{g^*})
y^m < \overline{y^m}
limited franchise
reduces public good provision
\overline{y^m}/y
\overline{g^*}
Evidence
There are so many studies exploring the relationship
between democracy and government expenditure
Some find no relationship; others find a positive association
But democracy may be mismeasured
Universal suffrage may not be actually enforced
Democracy is endogenous
More educated population demand
both more public good and more democracy
e.g.
Electronic voting in Brazil
Paper-based voting effectively disenfranchises those illiterate
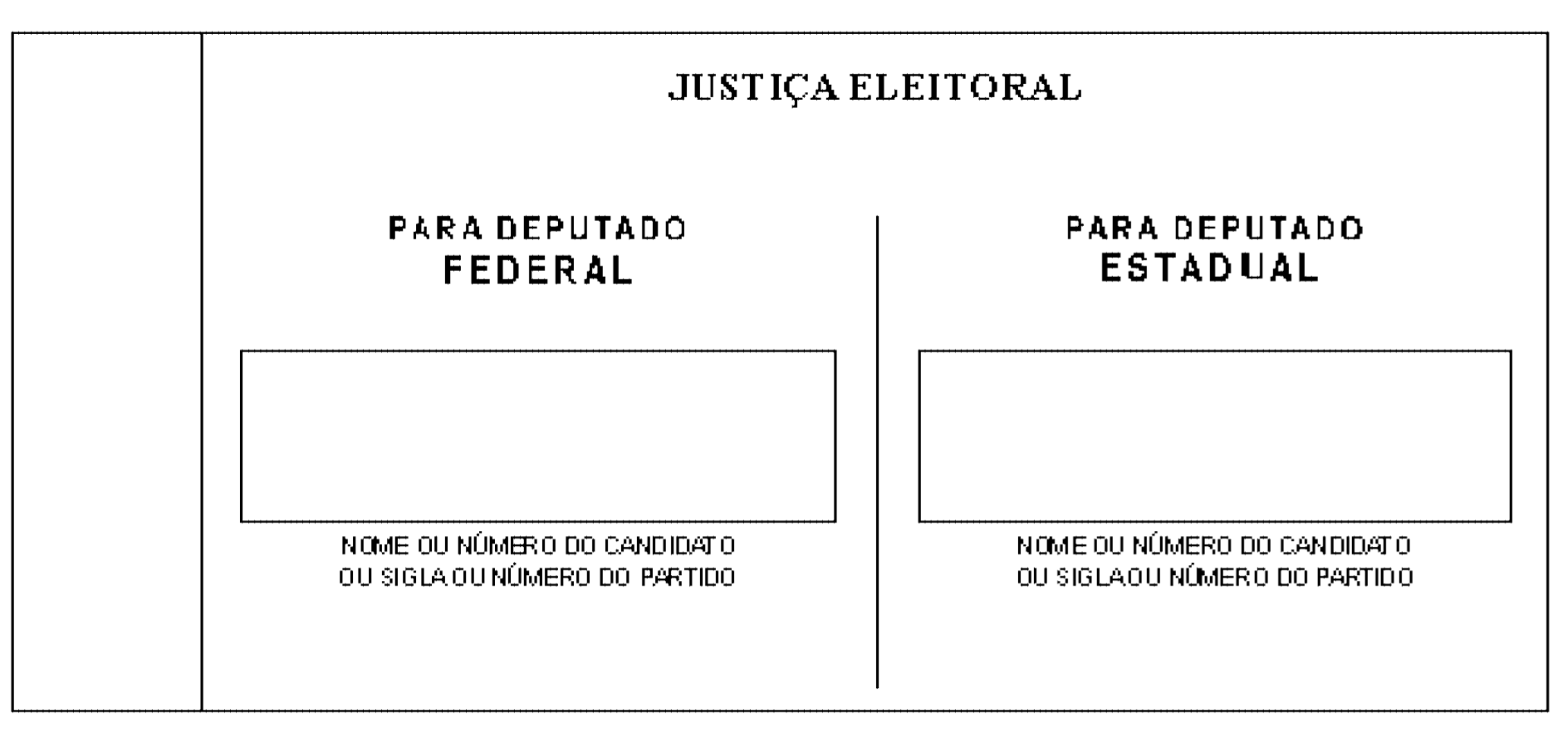
Image source: Figure 1 of Fujiwara (2015)
Electronic voting in Brazil
Electronic voting was introduced in the mid-1990s
Image source: Figure 1 of Fujiwara (2015)
Electronic voting in Brazil
If you enter the candidate number correctly...
Image source: Figure 1 of Fujiwara (2015)
Electronic voting in Brazil
If you enter a wrong number...
Image source: Figure A1 of Fujiwara (2015)
Electronic voting in Brazil
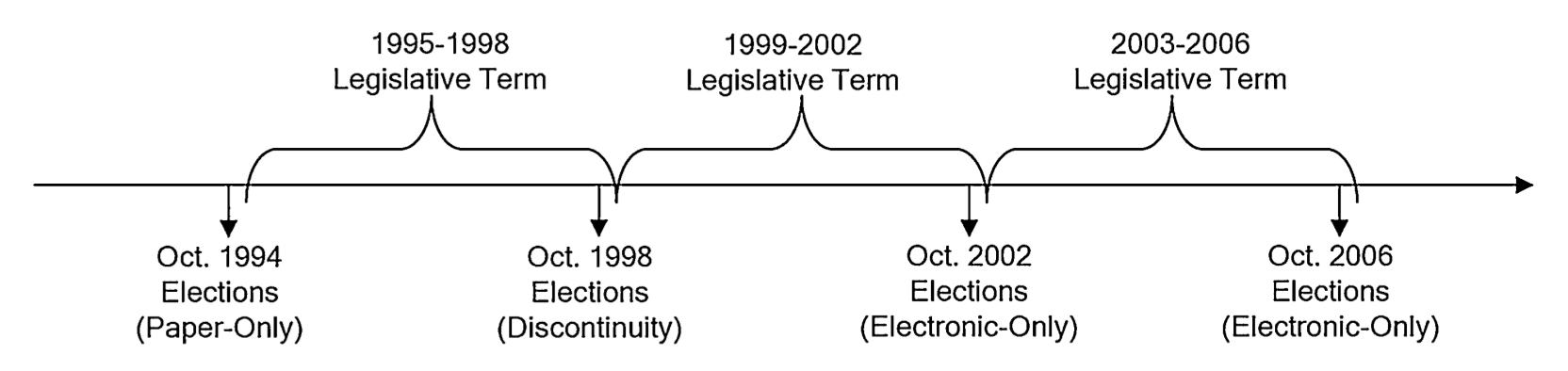
Brazil is a federation of 27 states
Every four years
each state holds elections for its legislature and governor
In 1994 elections, all states used paper-based voting
In 1998, municipalities with 40,500+ registered voters adopted electronic voting
In 2002, all used electronic voting
Electronic voting in Brazil
In 1998, municipalities with 40,500+ registered voters adopted electronic voting
If you compare municipalities just above the 40,500 threshold
with those just below...
Any difference in outcomes can be interpreted
as the impact of electronic voting
Regression Discontinuity Design
# of valid votes as % of turnout
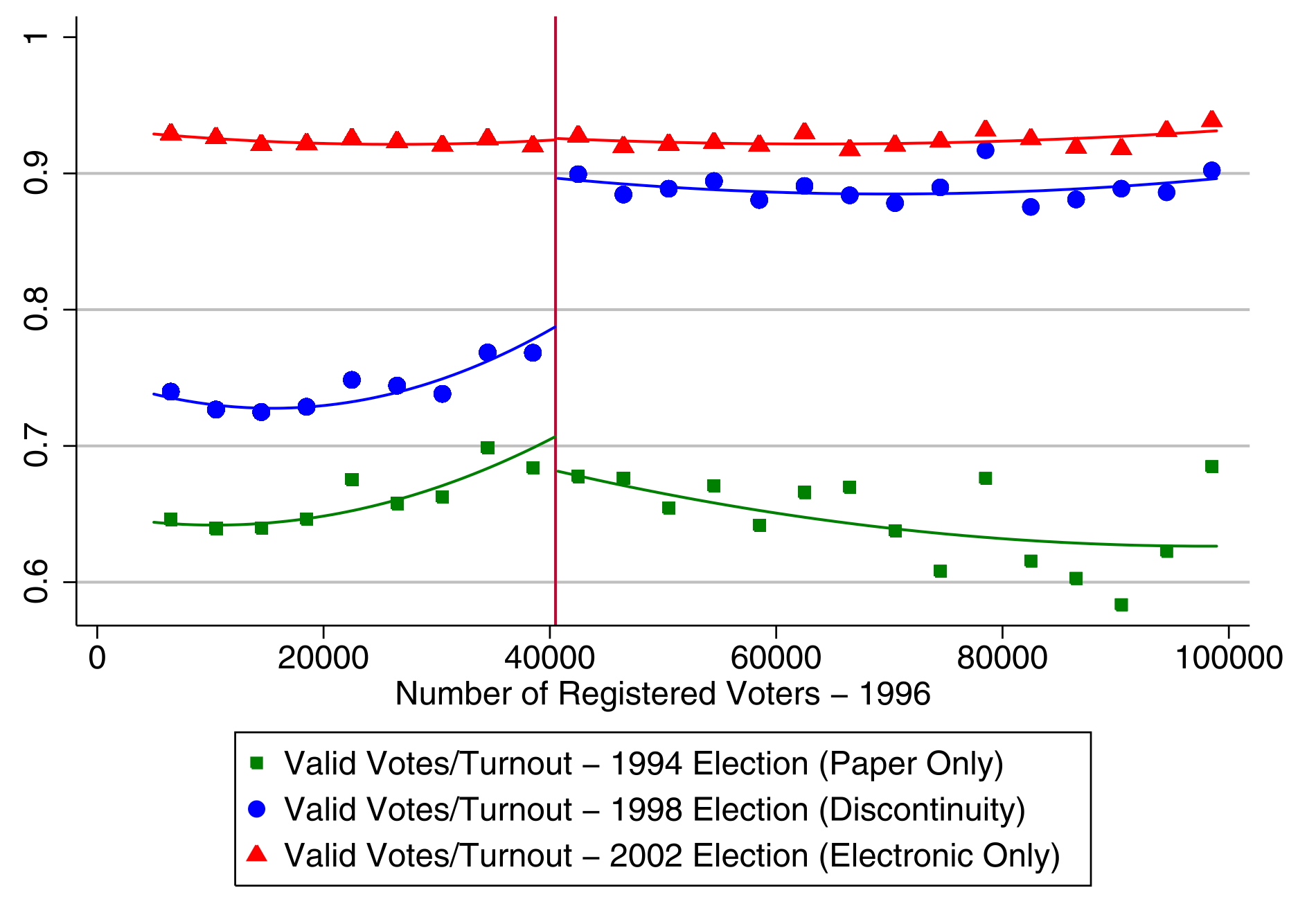
Image source: Figure 2 of Fujiwara (2015)
The 1996 elections were for state governments, not municipal
Image source: Figure 4 of Fujiwara (2015)
Policy outcomes
Policy outcomes are the same for municipalities within a state
We cannot use RDD for estimating the impact on policies
Instead...
Construct a state-level panel data
for every 4-year period from 1995-2006
Policy outcomes (cont.)
Obtain each state's share of registered voters in municipalities that introduced electronic voting in 1998, denoted by
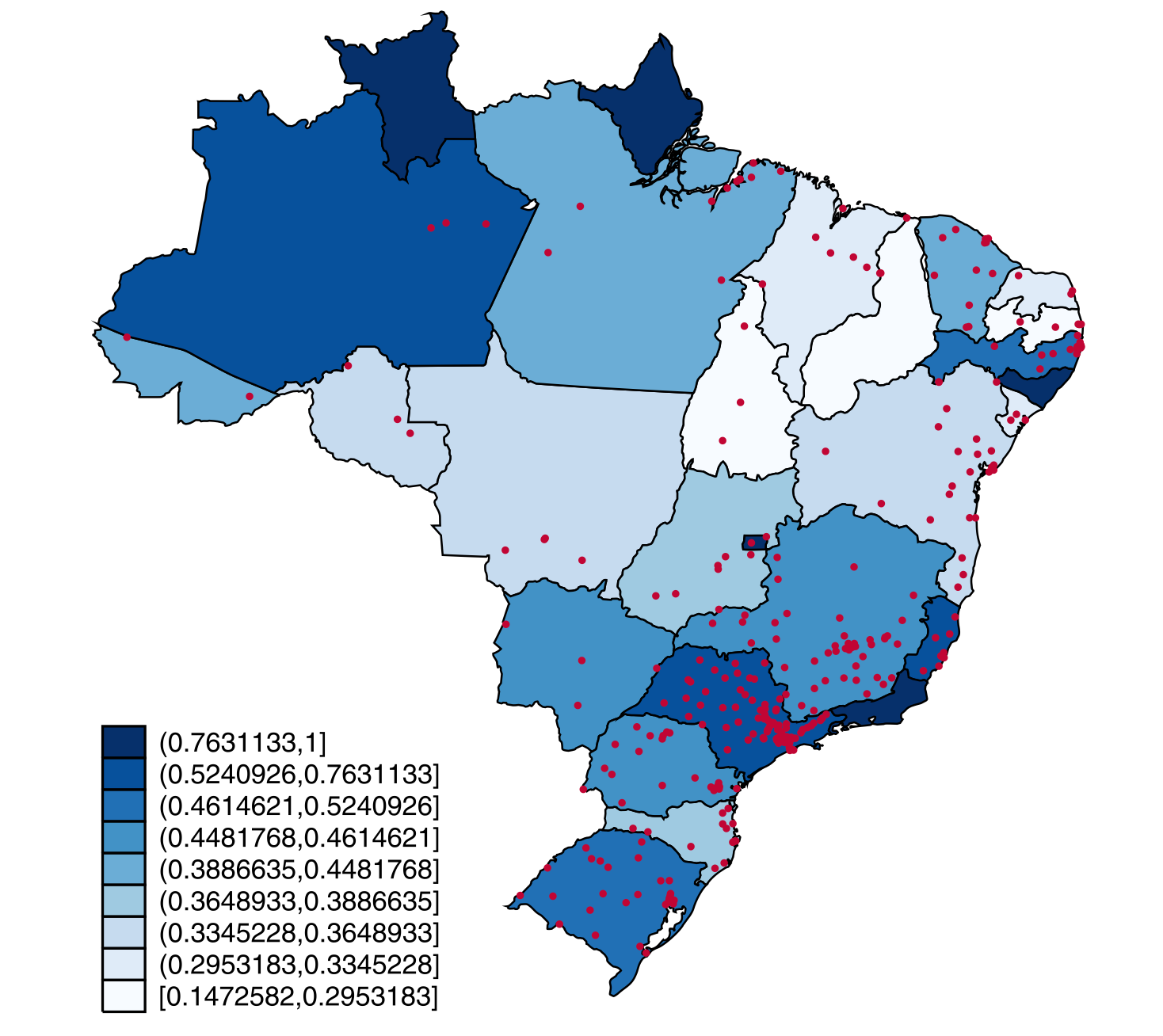
Image source: Figure 5 of Fujiwara (2015)
S_i
If electronic voting increases spending for the illiterate
the 1998 elections should cause a positive association
S_i
g^{99-02}_i-g^{95-98}_i
0
1
Impact of EV
If electronic voting increases spending for the illiterate
After the 2002 elections, all municipalities reach the same level
S_i
0
1
Impact of EV
g^{03-06}_i-g^{95-98}_i
If electronic voting increases spending for the illiterate
So the comparison between 99-02 and 03-06 yields
S_i
0
1
Impact of EV
g^{03-06}_i-g^{99-02}_i
Identifying assumption
No omitted variable exhibits the same reversal of an association with policy changes
S_i
\Delta g_{i,94-98}
S_i
\Delta g_{i,98-02}
Estimation equations
\Delta g_{ir,94-98} =\alpha^{98} + \beta^{98} S_i + \gamma^{98}_r + \varepsilon_{ir,94-98}
\Delta g_{ir,98-02} =\alpha^{02} + \beta^{02} S_i + \gamma^{02}_r + \varepsilon_{ir,98-02}
Predictions
\beta^{98}+\beta^{02}=0
\beta^{98} (= -\beta^{02})
Impact of electronic voting is given by
Region
fixed
effects
Results on policy
\hat{\beta}^{98}
\hat{\beta}^{02}
\frac{\hat{\beta}^{98}+\hat{\beta}^{02}}{2}
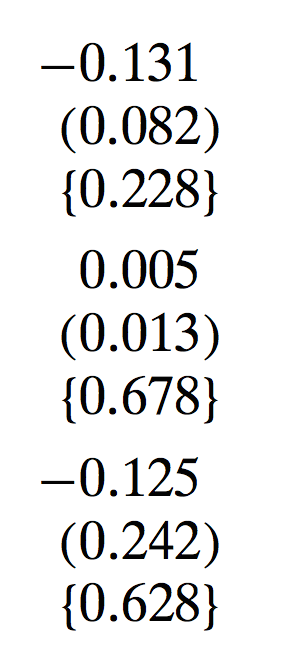
Health care spending goes up by 34% of the sample mean
Sample
Mean
Results on infant health
\hat{\beta}^{98}
\hat{\beta}^{02}
\frac{\hat{\beta}^{98}+\hat{\beta}^{02}}{2}
Final thought
The Median Voter Theorem is perhaps still useful for
Compare democracy to non-democracy
Introduce politics into a complicated model of the economy
Its most important implication is the centripetal force in politics
To obtain the majority,
politicians want to propose a centrist policy
(if they can commit)
Political Economics Lecture 1: Median Voter Theorem
By Masayuki Kudamatsu
