Parafermions at TRI interfaces?
Oroszlány László
Department of Physics of Complex Systems
Eötvös Loránd University, Budapest



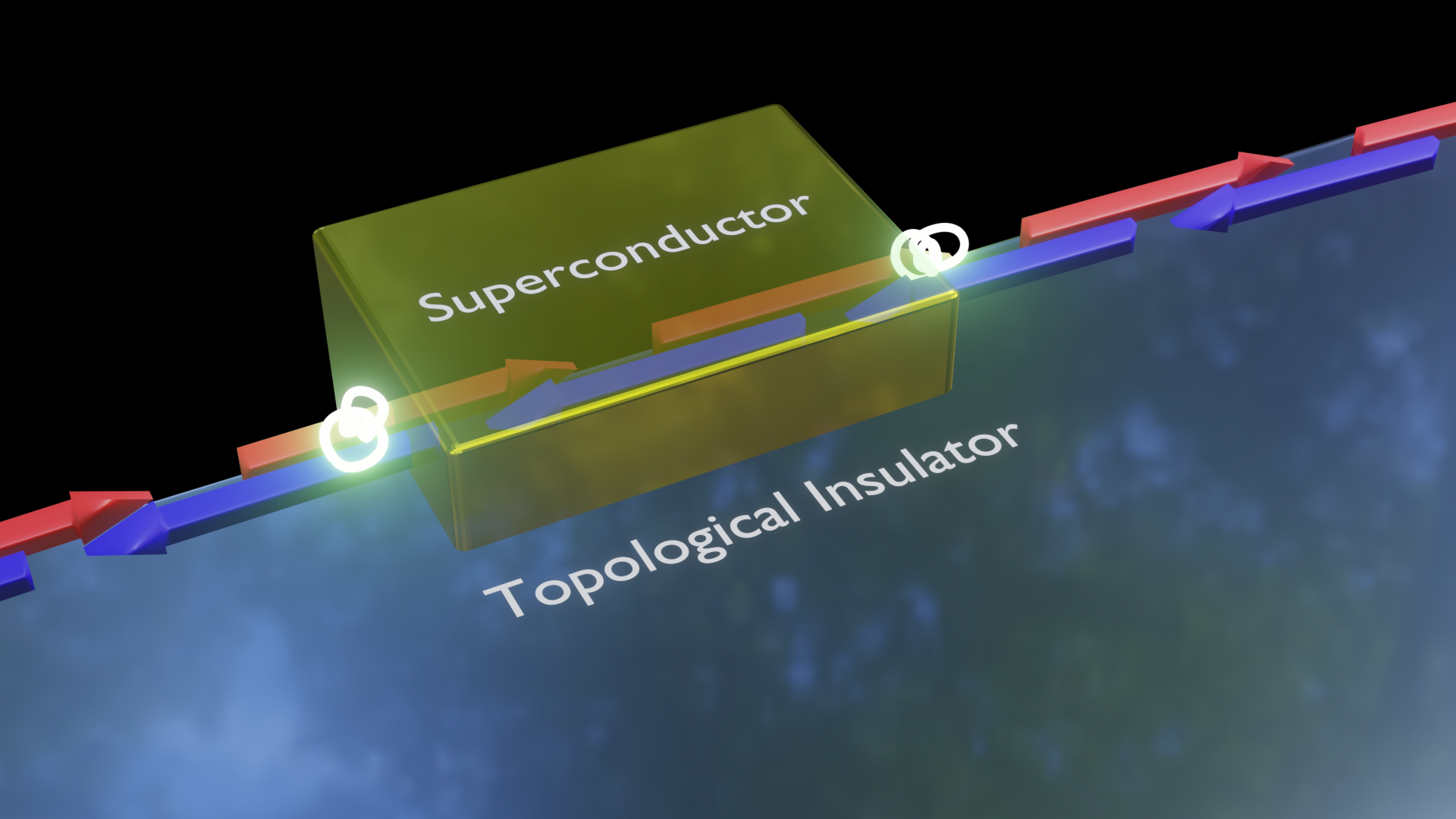
Topological quantum computer architectures
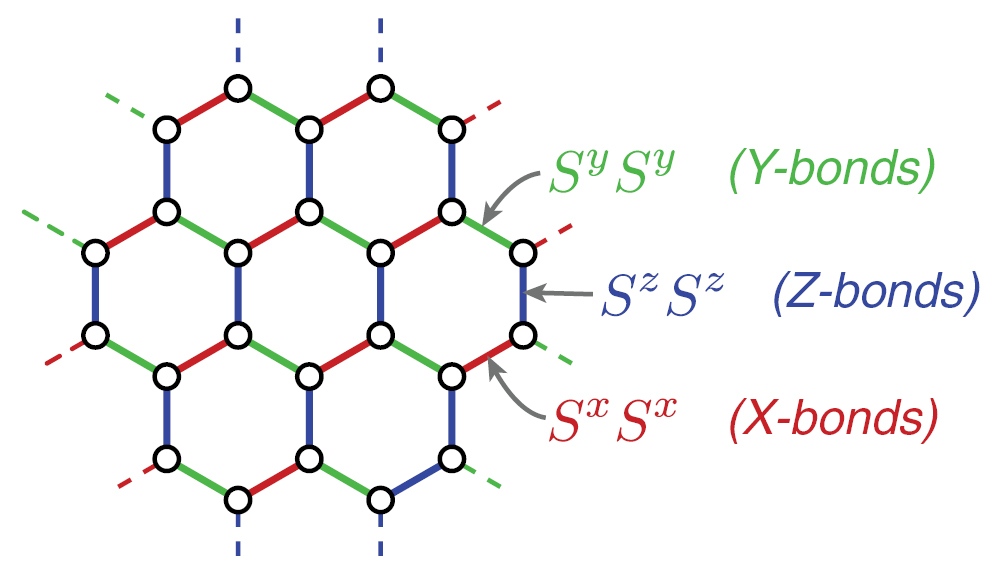
many physical qubit = few logical qubit
degenerate subspace\(\Leftrightarrow\) topology of real space
A. Kitaev, Annals of Physics 321 2 (2006)
|
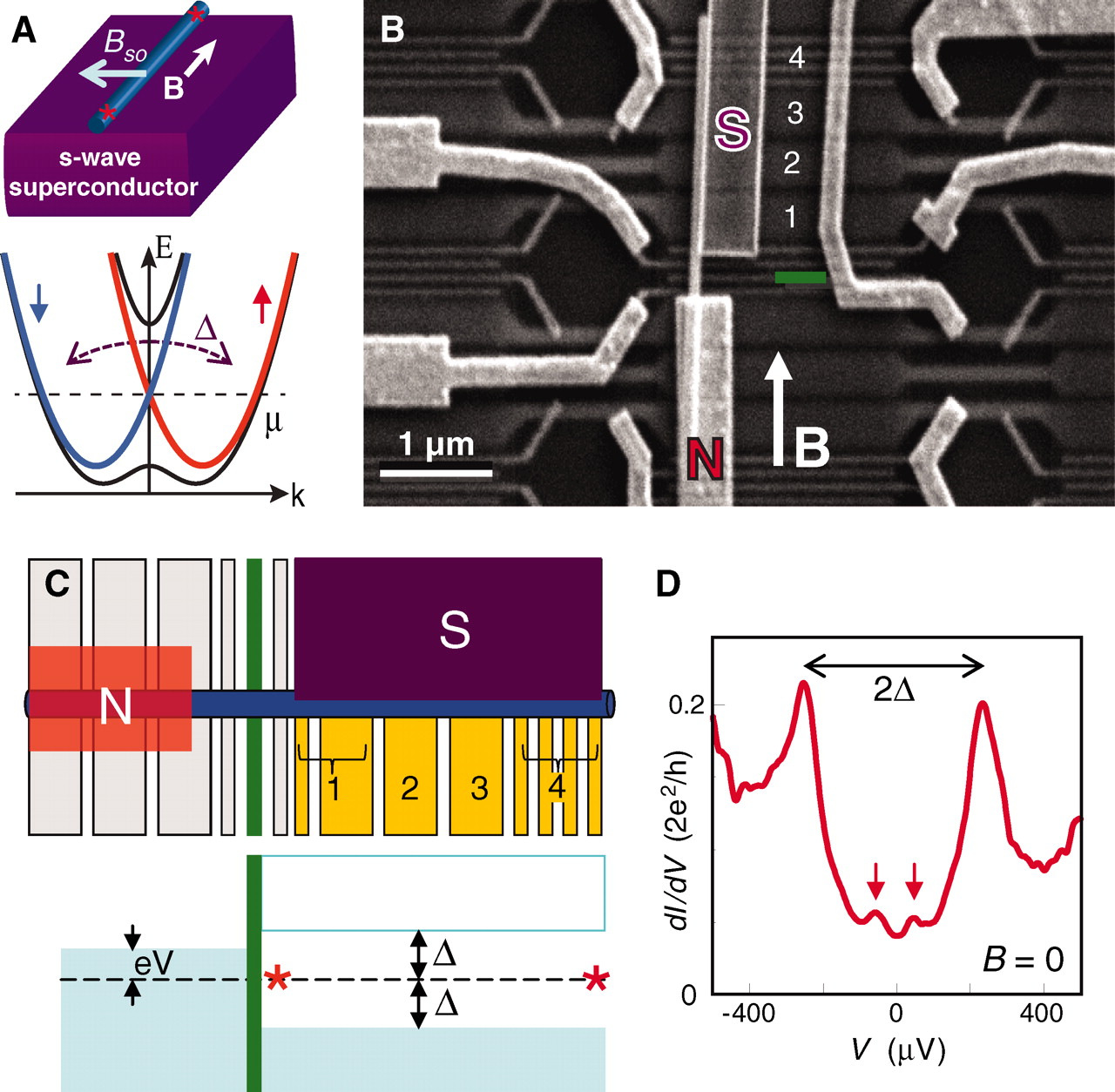
A. Kitaev Phys.-Usp. 44 131 (2001) R. Lutchyn et al. Phys. Rev. Lett. 105, 077001 (2010) Y.Oreg et al. Phys. Rev. Lett. 105, 177002 (2010) V. Murik et al. Science 336, 1003 (2012) |
topological protection
due to material properties
Majorana qubit
Kitaev "honeycomb" and "toric code"

Ising / Majorana / Topological superconductor
Jordan-Wigner
Majorana-fermion
"standard" fermion
TSC
p-wave
\(\hat{\gamma}_0\), \(\hat{\gamma}_{2L+1}\) absent!!
1D "transvers filed" Ising model
Kitaev model
Clock models and parafermions
\(f=0\rightarrow\) parafermions at the edg, \(\hat{\alpha}_1\) & \(\hat{\alpha}_{2L}\), absent form the Hamiltonian!
The missing two parafermions encode an N-fold degenerate subspace!
N=3 Clock model
Jordan-Wigner
Parafermion
Majorana-ferminok vs. parafermionok
- Majorana-fermionok nem "igényelnek" kölcsönhatást (átlagtér közelítés elegendő).
- Majorana-fermionok mozgatásának segítségével ugyan nem triviális kvanumkapuk megvalósíthatóak, de nincs univerzális kapukészlet, e.g. összefonó kaput nem lehet realizálni a topologikus védelem feladása nélkül.
- Parafermionokhoz szükséges a kölcsönhatás (átlagtér közelítésen túl kell lépni)!
- \(N>2\) parafermionok segítségével megvalósítható összefonó kapu, de ez még mindig nem elegendő univerzális kvantumszámításhoz.
A.Hutter, D. Loss Phys. Rev. B 93, 125105 (2016)
Possible experiment
F. Zhang, C. L. Kane, Phys. Rev. Lett., 113, 036401 (2014).
C. P. Orth et al. Phys. Rev. B, 91, 081406 (2015).
J. Alicea, P. Fendley Annu. Rev. Condens. Matter Phys. 7,119 (2016.)
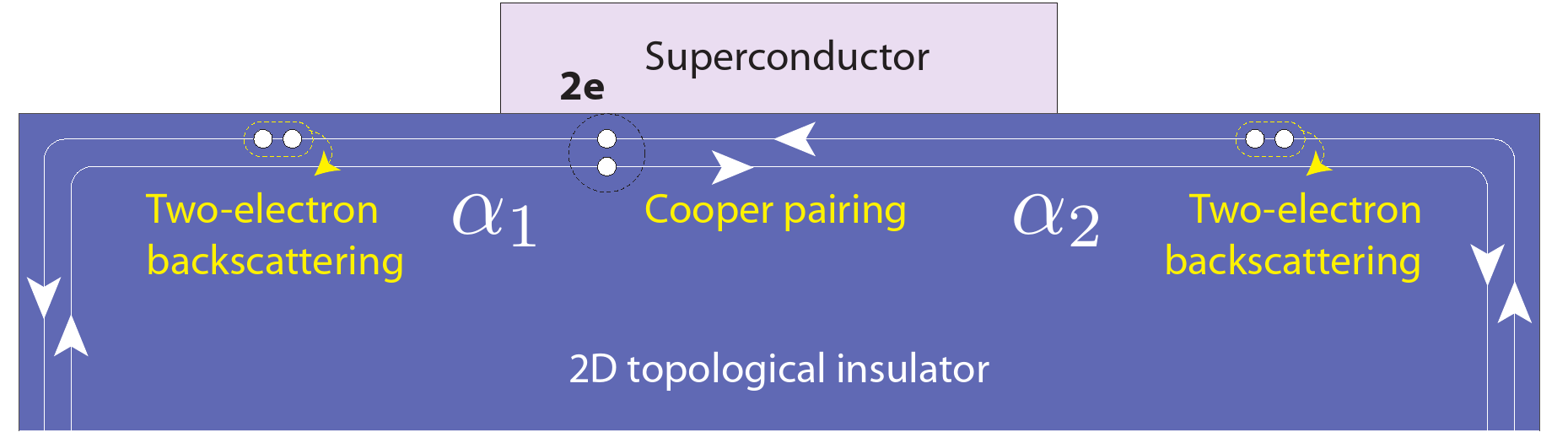
goal: microscopic model + DMRG
bosonised models
The model
- two "disconected edges" (\(\zeta = {L,R} \) )
- explicit superconductivity
- time reversal symmetry
L
R
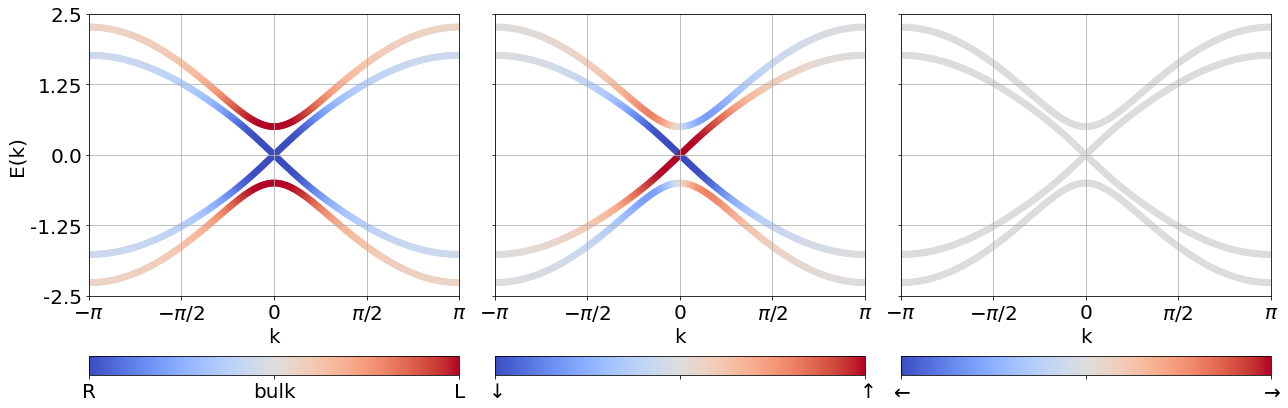
Single particle spectrum
small \(B_y\) on the left for better visibility
Finite size DMRG calculations
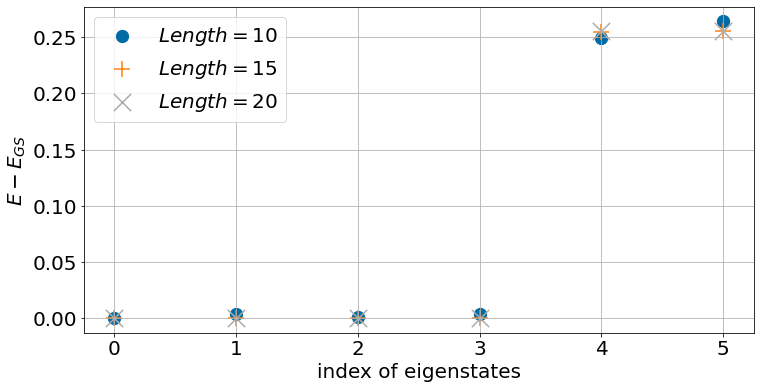
gap remains finite !
\(V_L=1.7,\Delta_R=0.7\)
Finite size DMRG calculations
\(Length=12,\Delta_R=0.7\)
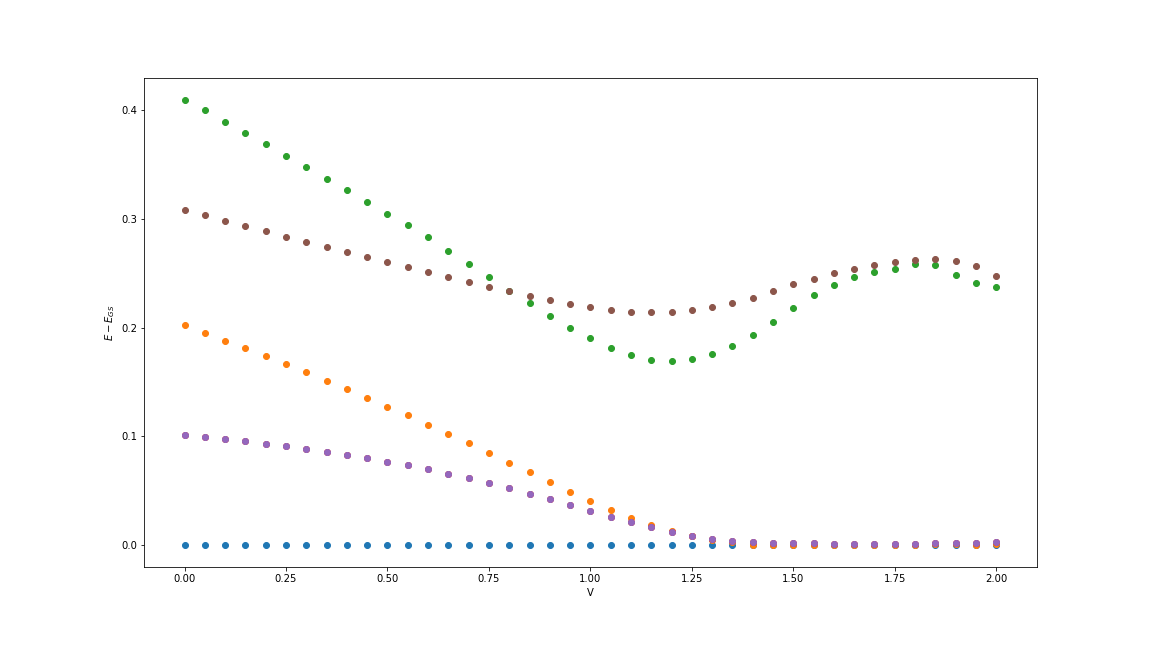
\(V_L\)
\(E-E_{GS}\)
4x degenerate!
gap !
no gap !
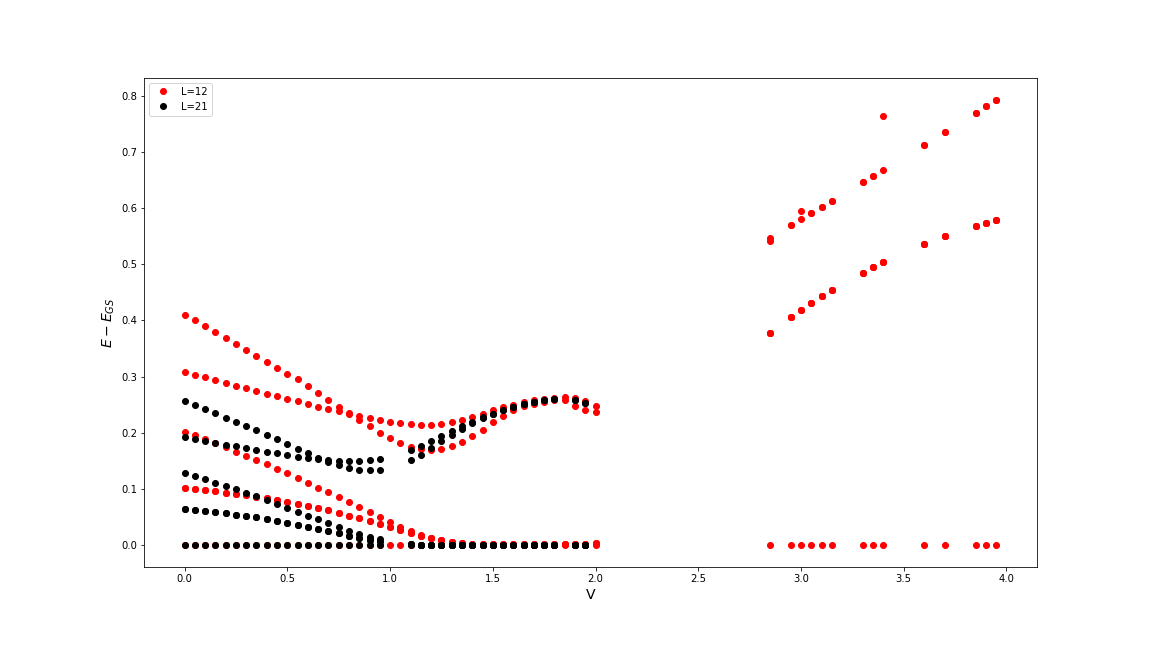
Properties of the ground state
\( \langle GS_p | n_i | GS_q \rangle \approx \delta_{pq} \)


Interface on one side


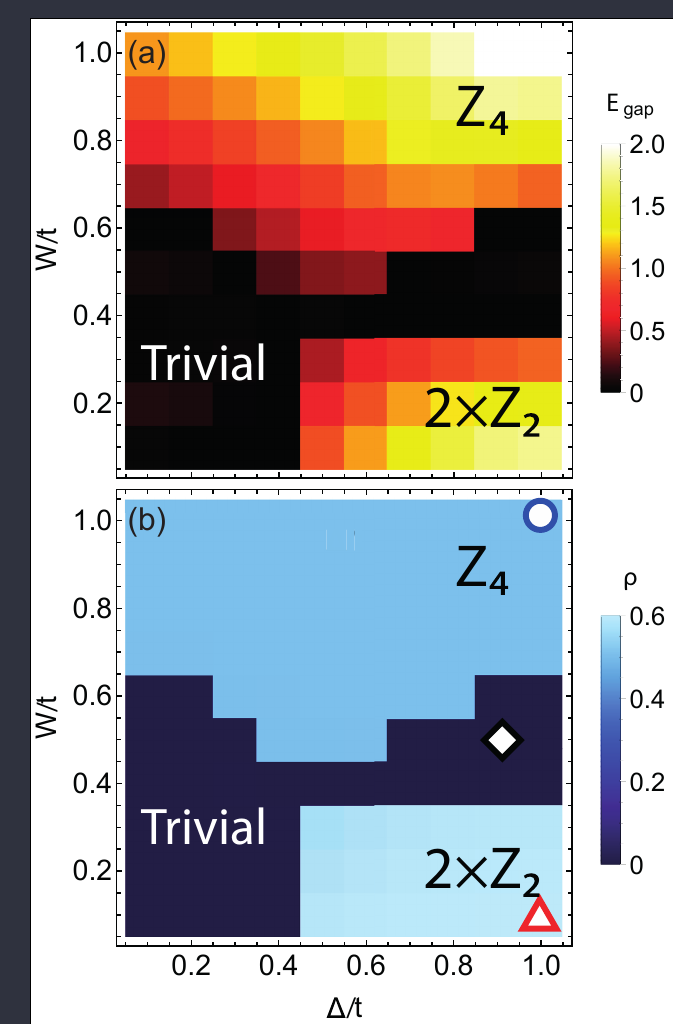
Raphael L. R. C. Teixeira, Luis G. G. V. Dias da Silva Phys. Rev. Research 3, 033014 (2021)
Phase diagram of the Clock model derived fermionic system
The team

Osváth Botond, ELTE

Barcza Gergely, Wigner
Thanks









Parafermion summary
By László Oroszlány
Parafermion summary
- 490



