My Attempt at Monads

Leon Tager
Zhia Chong
Software Engineer
Medium Blogger
(bit.ly/zhiastory)
Goals
Learn about
- Semigroup
- Monoids
- Functors
- Monoids
In a Explain-to-a-5-year-old manner

How did we get here?
☑ Immutable code
☑ Composing functions
☑ Higher order functions
☑ Currying
☑Recursion
At the start










Summingbird
Streaming MapReduce with Scalding and Storm
Monoids?
Scala
Lightweight, modular, and extensible library for functional programming

Monads?
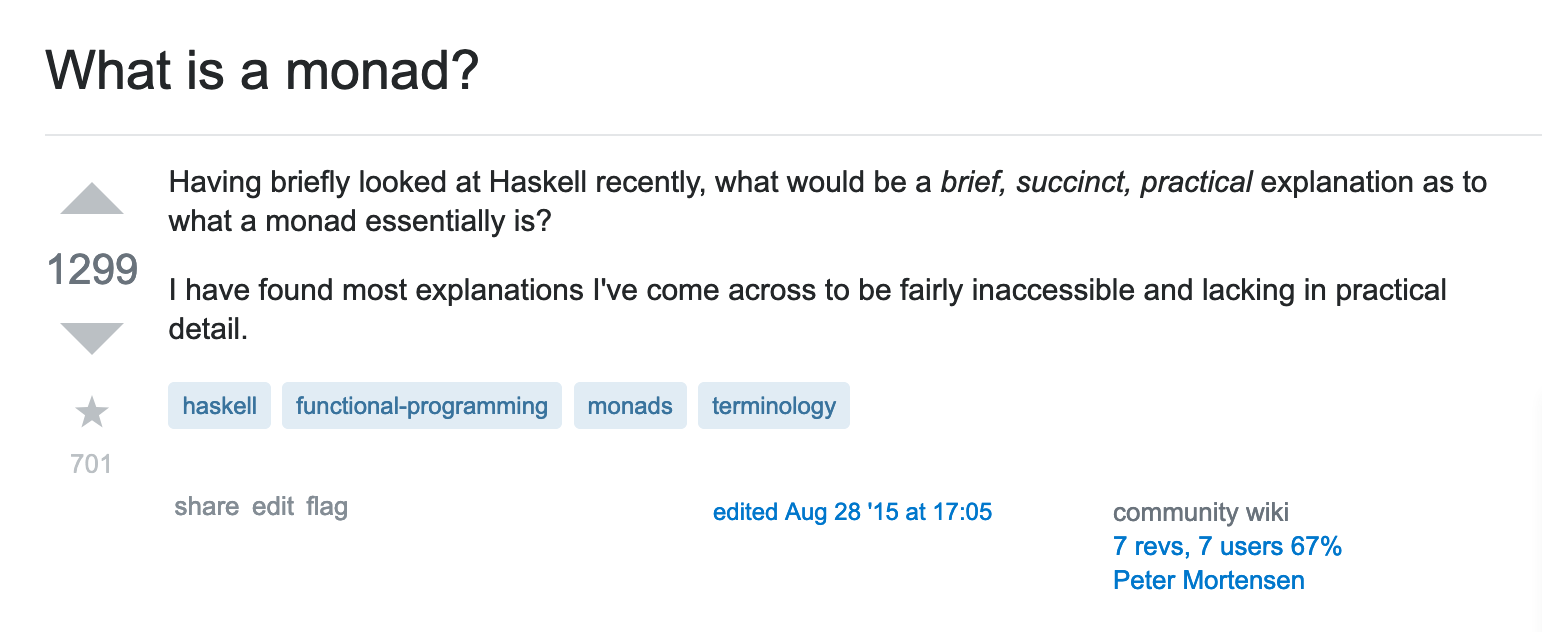
Help!
infixl 1 >>, >>=
class Monad m where
(>>=) :: m a -> (a -> m b) -> m b
(>>) :: m a -> m b -> m b
return :: a -> m a
fail :: String -> m a
m >> k = m >>= \_ -> kThis doesn't help


functor
Alt
Plus
Alternative
Apply
Applicative
Monad
Bifunctor
Extend
Comond
Profunctor
Traversable
Foldable
Semigroupoid
Category
Setoid
Ord
Contravariant
Filterable
Semigroup
Monoid
Group
functor
Monad
Semigroup
Monoid
Semigroups
It's just an operation
Semigroups
It's just an operation



Semigroups - what is it?
// here's our definition of a semigroup
trait Semigroup[A] {
// some binary operation for you to define
def op(x: A, y: A): A
}
And...
Semigroup rules
Associativity - order of operation doesn't matter
// (1 + 2) + 3 = 1 + (2 + 3)
op(x, op(y, z)) = op(op(x, y), z)Closure - operation on members of a set always makes a member of the same set
// (A, A) -> A
def op(x: A, y: A): AExamples of Semigroup
val intMaxSemigroup: Semigroup[Int] = new Semigroup[Int] {
def op(x: Int, y: Int): Int = math.max(x, y)
}val intMinSemigroup: Semigroup[Int] = new Semigroup[Int] {
def op(x: Int, y: Int): Int = math.min(x, y)
}val list = Seq(1, 2, 3)
list.reduce(intMaxSemigroup.op) // 3
list.reduce(intMinSemigroup.op) // 1// But what will happen here?
val list = List.empty[Int]
list.reduce(intMaxSemigroup.op)java.lang.UnsupportedOperationException: empty.reduceLeft
at scala.collection.LinearSeqOptimized.reduceLeft(scratch_10.scala:131)
at scala.collection.LinearSeqOptimized.reduceLeft$(scratch_10.scala:130)
at scala.collection.immutable.List.reduceLeft(scratch_10.scala:82)
at scala.collection.TraversableOnce.reduce(scratch_10.scala:204)
at scala.collection.TraversableOnce.reduce$(scratch_10.scala:204)
at scala.collection.AbstractTraversable.reduce(scratch_10.scala:100)
at #worksheet#.get$$instance$$res0(scratch_10.scala:19)
at #worksheet#.#worksheet#(scratch_10.scala:51)// here's our definition of a semigroup
trait Semigroup[A] {
// an associative operation
def op(x: A, y: A): A
}
// Subtraction is not associative
scala> ((1 - 2) - 3)
res0: Int = -4
scala> (1 - (2 - 3))
res1: Int = 2Examples of a non-Semigroup
Semigroup
Do stuff to two things
Monoids
It's just an operation with a default
Monoids
It's just an operation with a default


Monoids - what is it?
// Monoid, like a semigroup is a definition of an operation
// with an identity value
trait Monoid[A] {
def op(a1: A, a2: A): A
def empty: A
}And...
Monoid rules
Associativity - order of operation doesn't matter
// (1 + 2) + 3 = 1 + (2 + 3)
op(x, op(y, z)) = op(op(x, y), z)Closure - operation on members of a set always makes a member of the same set
// (A, A) -> A
def op(x: A, y: A): AIdentity
// 1 + 0 = 0 + 1 = 1
op(x, id) == op(id, x) == xFamiliar?
If op meets the rules on type M then we say M forms a monoid under op.
Terminology
If addition meets the rules on type natural numbers then we say natural numbers form a monoid under addition.
Examples of a monoid
// but wait, there's more
trait Monoid[A] extends Semigroup[A] {
def empty: A
}val stringMonoid = new Monoid[String] {
def op(a1: String, a2: String) = a1 + a2
def empty = ""
}val intMultiplication = new Monoid[Int] {
def op(x: Int, y: Int) = x * y
val empty = 1
}val list = Seq(1, 2, 3)
list.foldLeft(intMultiplication.empty)(intMultiplication.op) // 6
val emptyList = List.empty[Int]
emptyList.foldLeft(intMultiplication.empty)(intMultiplication.op) // 1Much better
// here's our definition of a monoid
trait Monoid[A] {
// an associative operation
def op(a1: A, a2: A): A
// an identity element
def empty: A
}Monoid
semigroup with an identity
Monoids
Semigroup
Monoid - in other words
Monoid -why should I care?
Closure, Associativity and Identity
Monoids are everywhere.
-
Thanks to closure, we can combine and aggregate things.
-
Thanks to associativity, we can do it in parallel.
-
Thanks to identity, we know what to do when we don't have anything to start off with.

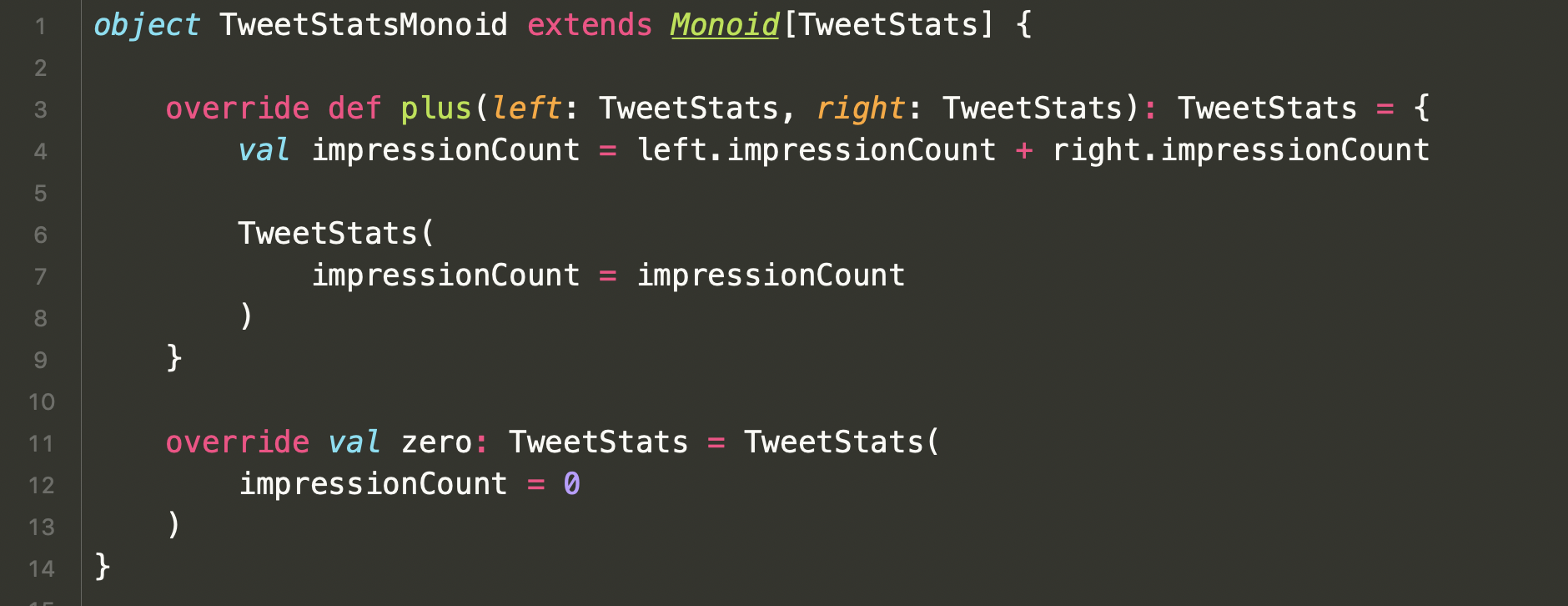
Monoid - How we use it at Twitter

Functors
Take this and turn it into that




Functors - what is it?
Functors - what is it?
// It's a wrapper
trait Functor[F[_]] {
// It has a map method
def map[A,B](fa: F[A])(f: A => B): F[B]
}And...
Functor rules
Composition
// Mapping with g and then f is the same as
// Mapping both at the same time.
functor.map(g).map(f) == functor.map(x => f(g(x)))Identity
// passing the identity function
// returns the same functor back
// (in the mathematical sense)
functor.map(x => x) == functor// Example for an option
// (Basically the same old option.map)
val functorForOption: Functor[Option] = new Functor[Option] {
def map[A, B](fa: Option[A])(f: A => B): Option[B] = fa match {
case None => None
case Some(a) => Some(f(a))
}
}
val option = Option(1)
functorForOption.map(option)(a => a + 1) // Option(2)// definition of a functor
trait Functor[F[_]] {
// It has a map method
def map[A,B](fa: F[A])(f: A => B): F[B]
}Examples of functors
Examples of non-functors
// Breaks the identity law
val notAFunctor: Functor[List] = new Functor[List] {
def map[A, B](fa: List[A])(f: A => B): List[B] = fa match {
case _ => List.empty[B]
}
}val list = List(1, 2, 3)
notAFunctor.map(list)(x => x) // res1: List[Int] = List()Examples of non-functors
// Breaks the composition law
val notAFunctor2: Functor[Option] = new Functor[Option] {
var prop = 0
def map[A, B](fa: Option[A])(f: A => B): Option[B] = fa match {
case None => None
case Some(a) => {
prop += 1
if (prop == 1) Some(f(a)) else None
}
}
}val f: Int => Int = x => x + 1
val g: Int => Int = y => y + 2notAFunctor2.map(Option(1))(z => f(g(z))) //Option[Int] = Some(4)notAFunctor2.map(
notAFunctor2.map(Option(1))(g)
)(f) // None :-(Functor in pictures
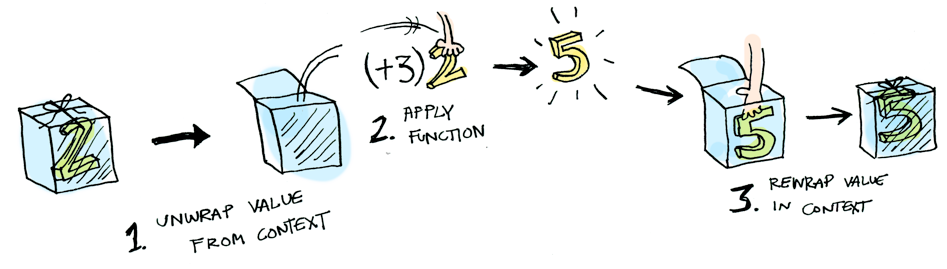
Monads
Take this and turn it into that ++



Monads - what is it?


Monads - what is it?
And...
// It's a wrapper
trait Monad[F[_]] {
// It has two methods
def unit[A](a: => A): F[A]
def flatMap[A, B](ma: F[A])(f: A => F[B]): F[B]
}Monad rules
Associative
// Mapping with f and then g is the same as
// Mapping both at the same time.
x.flatMap(f).flatMap(g) == x.flatMap(a => f(a).flatMap(g))Identity
// Left identity
flatMap(x)(unit) == x// Right identity
flatMap(unit(y))(f) == f(y)Examples of monads
You already use them
- List
- Future*
- Option
- Try
- Either
Monads
Functors
Monads - in other words
Monad - use cases
def getUser(id: Long): Future[User]
def getHistory(user: User): Future[History]def getHistoryById(id: Long): Future[History] = getHistory(getUser(id))def getHistoryById(id: Long) = getUser(id) match {
case Success(user) => getHistory(user)
case Failure(_) => this.asInstanceOf[Future[S]]
}def getUser(id: Long): Option[User]
def getHistory(user: User): Option[History]def getHistoryById(id: Long) = getUser(id) match {
case Some(user) => getHistory(user)
case None => None
}Lists, Try, Either? This is going to be a long night

Monad - use cases
def getUser(id: Long): Future[User]
def getHistory(user: User): Future[History]def getHistoryById(id: Long): Future[History] = getUser(id).flatMap(getHistory)// Which is the same as
val res: Future[History] = for {
u <- getUser(0)
h <- getHistory(u)
} yield hMonads are great when evaluation of your function depends on the value of the previous function
Monad
Functor with a flatMap
Monad - fun fact
Functors compose. Monads don't
// Have you ever had to deal with
Option[List[A]]// Have you ever tried to map over it?
optionalList.map(_.map(f))Turns out that if F and G are functors, so is F[G[_]] for any functor
Composition of monads does not guarantee the result is a monad.

Things that confused me
Sometimes it's map, sometimes it's >>
Sometimes it's flatMap, sometimes it's join
Sometimes it's flatMap, sometimes it's join
trait Monad[F[_]] {
def unit[A](a: => A): F[A]
def flatMap[A, B](ma: F[A])(f: A => F[B]): F[B]
}trait Monad[F[_]] {
def unit[A](a: => A): F[A]
def map[A,B](fa: F[A])(f: A => B): F[B]
def join[A](fa: F[F[A]]): F[A]
}trait Monad[F[_]] {
def unit[A](a: => A): F[A]
// Composing Kleisli arrows
def compose[A,B,C](f: A => F[B], g: B => F[C]): A => F[C]
}A monad needs to satisfy the rules mentioned earlier - associativity and identity. The interface is not important.
I can't find any of these interfaces in Scala
Summary of key points
| Semigroup | An operation on two objects | op: (A, A) -> A |
| Monoid | A an operation with a default | op: (A, A) -> A identity: A |
| Functor | Something that can be mapped over | map F[A] ->(A -> B): F[B] |
| Monad | A functor that unwrapes the top layer | flatMap F[A] -> (A -> F[B]): F[B] |
A monad is just a monoid in the category of endofunctors, what's the problem?
Thank you

My attempt at monads
By Leon Tager
My attempt at monads
- 272


