Tomografia & Emaranhamento
em Estados Quânticos de Variáveis Contínuas
Ludmila Augusta Soares Botelho
Departamento de Física - ICEx - Universidade Federal de Minas Gerais
representações
(e limitadas)
porém boas o suficiente!
Representações
Discretos
Contínuos
Experimento
Dados
Mecânica Quântica
Dados
Estado Quântico
Representações
Discretos
Contínuos
Estados Quânticos
Discretos
Contínuos
\vert \uparrow \rangle = \begin{bmatrix}
1\\
0\\
\end{bmatrix}
\vert \downarrow \rangle = \begin{bmatrix}
0\\
1\\
\end{bmatrix}
\vert 0 \rangle = \begin{bmatrix}
1\\
0\\
\end{bmatrix}
\vert 1 \rangle = \begin{bmatrix}
0\\
1\\
\end{bmatrix}
$$\left\vert \Phi^{+} \right\rangle = \frac{\vert 00 \rangle + \vert 11 \rangle }{\sqrt{2}}$$
$$i\hbar \frac{\partial}{\partial t}\Psi(\mathbb{r},t)=\left[ \frac{-\hbar^2}{2m}\nabla^2+V(\mathbb{r},t)\right]\Psi(\mathbb{r},t)$$
E o video game?
Também começou do contínuo!
Estados Quânticos
-
Operador Densidade
\rho = \rho^\dagger
\rho \geq 0
\mathrm{tr}(\rho)= 1
Estados Quânticos
\rho =\begin{bmatrix}
a_{11} & \dots & a_{1n} \\
\vdots & \ddots & \vdots \\
a_{n1} & \dots & a_{nn}
\end{bmatrix}
-
Dimensão
Estados Quânticos
\rho =\begin{bmatrix}
\quad & \quad & \quad \\
\quad & \text{\Huge?} & \quad \\
\quad & \quad & \quad
\end{bmatrix}
-
Dimensão infinita
Espaço de Fase
- Função de Wigner
$$W(q,p) = \frac{1}{2\pi\hbar} \int \left\langle q-\frac{v}{2}\right\vert \rho\left\vert q+\frac{v}{2}\right\rangle e^{ipv/\hbar}\mathrm{d}v$$
- Pode assumir valores negativos
- "Quase-probabilidade"
Espaço de Fase
Propiedade
Espaço de Hilbert
Espaço de Fase
Dimensão
Estrutura
$$\infty$$
$$2N$$
$$\otimes$$
$$\oplus$$
$$\mathcal{H}$$
Gaussianos
Descrição
$$\rho$$
$$\mathbf{d},\mathbf{\sigma}$$
$$\Gamma$$
Detecção Homódina
2-1
$$\vert \alpha \rangle$$
signal
50/50
Intensidade Número de fótons
$$I_{21} = I_1 - I_2$$
$$ \propto$$
(balanceada)
\hat{n}_1=\hat{a}_1'^\dagger\hat{a}_1' \qquad \hat{n}_2=\hat{a}_2'^\dagger\hat{a}_2'\\
\hat{a}_1'=2^{1/2}(\hat{a}'-\alpha_{LO}) \qquad \hat{a}_2'=2^{1/2}(\hat{a}'+\alpha_{LO}) \\
\hat{n}_{21} = \hat{n}_{2} - \hat{n}_{1} = \alpha_{LO}^*\hat{a}+\alpha_{LO}\hat{a}^{\dagger} \\
\alpha = \vert\alpha_{LO}\vert(\cos{\theta} +i\sin{\theta}) \\
\hat{n}_{21} = \frac{1}{\sqrt{2}} \vert{\alpha_{LO}}\vert \left[ (\cos{\theta} +i\sin{\theta})(\hat{q} - i\hat{p}) + (\cos{\theta} +i\sin{\theta})(\hat{q} - i\hat{p}) \right]\\
\hat{n}_{21} = \frac{2}{\sqrt{2}}\vert{\alpha_{LO}}\vert\hat{q}_{\theta}
\langle{q_{\theta}}\vert\rho \vert{q_{\theta}}\rangle = \frac{1}{2\pi\hbar} \int_{-\infty}^{\infty} W(q_{\theta}\cos{\theta} - p_{\theta}\sin{\theta},q_\theta \sin{\theta} + p_{\theta}\cos{\theta}) \mathrm{d}p_{\theta}
Tranformada de Radom
$$\langle{q_{\theta}}\vert\rho \vert{q_{\theta}}\rangle \rightarrow W(q,p)$$
$$W(q,p) \rightarrow \langle{q_{\theta}}\vert\rho \vert{q_{\theta}}\rangle $$
?
W(q,p) = \frac{1}{2 \pi^{2}} \int_{-\infty}^{+\infty} \int_{0}^{\pi} pr(x,\theta) K(q\cos{\theta} + p\sin{}\theta -x) \mathrm{d}x \mathrm{d}\theta
Radom Inversa
K(x)= \frac{1}{2} \int_{-\infty}^{+\infty} \vert{\xi}\vert \exp{(i\xi x)} \mathrm{d}\xi
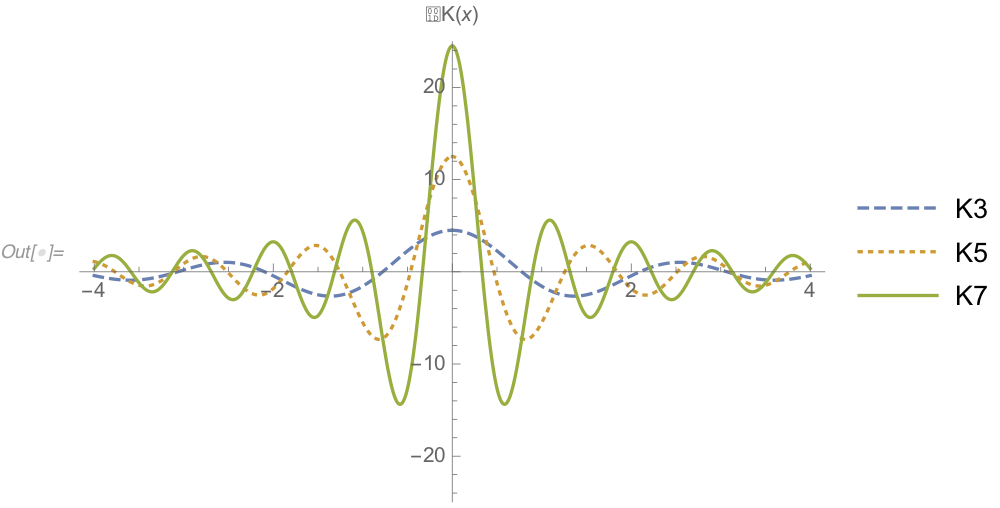
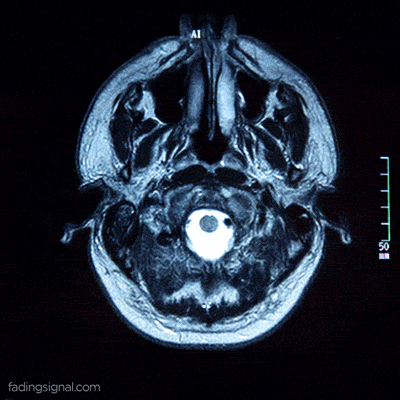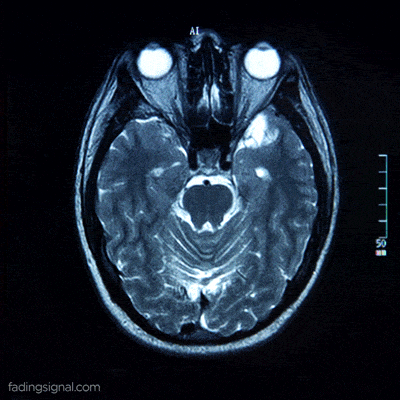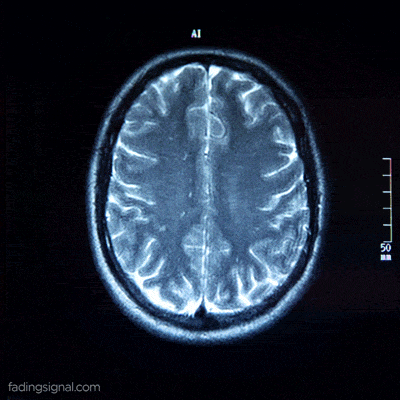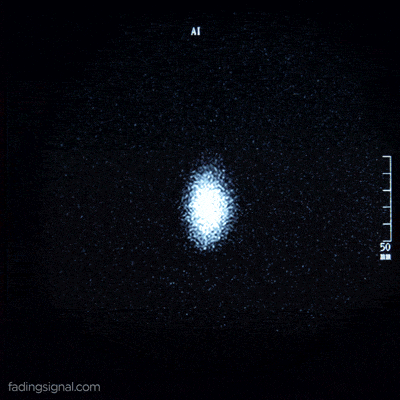
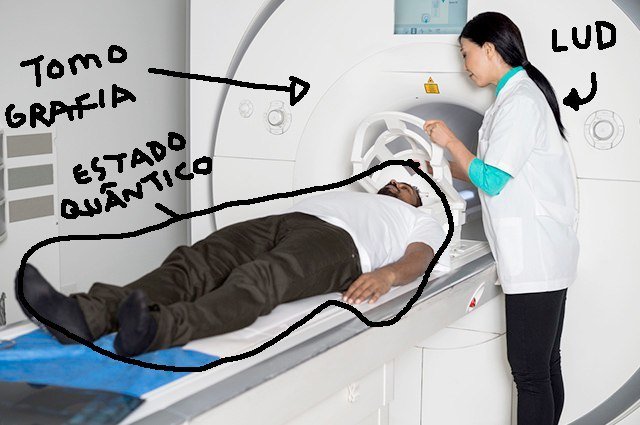
E se for de muitos modos?
Otimização Convexa
maximize
minimize
sujeito a
$$\vec{a}\cdot \vec{x}$$
$$\vec{\beta}_i\cdot \vec{x}= b_i$$
$$\vec{\gamma}_j\cdot \vec{x} \leq c_j$$
-
Problemas Lineares
$$ \vec{x}\geq 0 $$
$$i=1,\dots,m $$
$$j=1,\dots,n$$
Otimização Convexa
min
s.t
$$\rho \succeq 0$$
$$\mathrm{Tr}(\rho) = 1$$
-
Programação Semidefinida
-
Base de Fock
$$\sum_{i \in \mathcal{I}} \Delta_i + \delta$$
$${\rho, \Delta, \delta}$$
$$\left\vert \mathrm{Tr}({E_i \rho) -f_i} \right\vert \leqslant \Delta_i f_i$$
$$i \in \mathcal{I}$$
$$\mathrm{Tr}({ E_i\rho} )\leqslant \delta$$
$$i \notin \mathcal{I}$$
$$\vert q_{\theta}\rangle\!\langle{q_{\theta}}\vert= \sum \psi_n^*(q) \psi_m(q) \exp[i(m-n)]\vert{n}\rangle\!\langle{m}\vert$$
E agora para algo complemente diferente
Emaranhamento
- Separabilidade
$$\rho_{AB} = \sum_\lambda \pi (\lambda)\rho_A^\lambda \otimes \rho_B^\lambda$$
Critérios de Separabilidades
- Transposição Parcial
$$\rho^{T_B} = \sum_i p_i \left(\rho_i^A \otimes (\rho_i^B)^T\right)$$
Dimensão Grande
Critérios de Separabilidades
- Matriz de Covariância
\gamma \geq \begin{pmatrix}
\gamma_A & 0 \\
0 & \gamma_B
\end{pmatrix}
- SDP
Mapas Positivos
- Operador Densidade vs Matriz de Momentos
- Testemunha de Emaranhamento
(Porém Não Completamente Positivos)
Sep
$$\rho$$
$$\mathit{W}$$
Ent
$$M$$
$$\mathit{W}'$$
Obrigada!
Tomografia e Emaranhamento CV - Versão Extendida
By ludmilaasb
