Luisa Cutillo1, Valeria Policastro2, Annamaria Carissimo2

Robustness in Weighted Networks

1 University of Leeds, UK

2 IAC, CNR, Naples, Italy

Networks in maths

Networks are mathematical representations of interactions among the components of a system and can be modelled by

graphs

  • Components: Nodes, Vertices
  • Interactions: Links, Edges
  • Systems: Network, Graph              
  • V
  • E
  • G=(V,E)              

Networks in maths

Networks are mathematical representations of interactions among the components of a system and can be modelled by

graphs

  • Components: Nodes, Vertices
  • Interactions: Links, Edges
  • Systems: Network, Graph              
  • V
  • E
  • w: E-->R
  • G=(V,E, w)   

Weighted Case

How to extract information out of a Network?

  • vertices can be divided in groups

  • nodes belonging to the same group are densely connected

  • number of edges between nodes of different groups is minimal

Community Extraction, i.e. Graph Partitioning

Community

structure!

Research Questions

  • communities of real world networks are not always defined objectively

  • they rarely have a unique community decomposition

  • which method to use?

  • computationally difficult task

  • number of communities, if any, is typically unknown

  • communities are often of unequal size and/or density

  • can we trust the recovered partition? Is it statistically significant?

ROBustness In Network (robin): an R Package for Comparison and Validation of Communities [R journal (2021)]

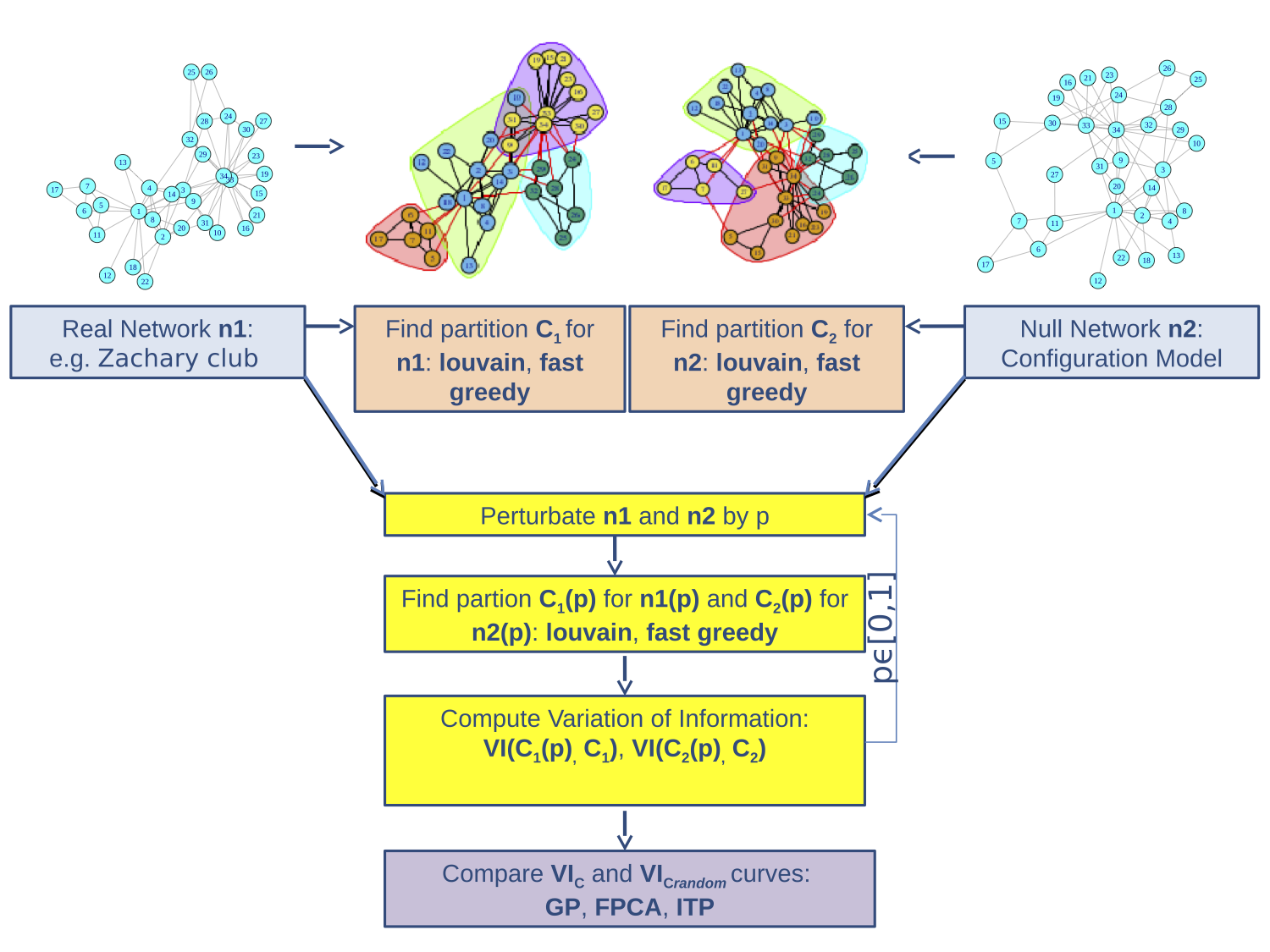
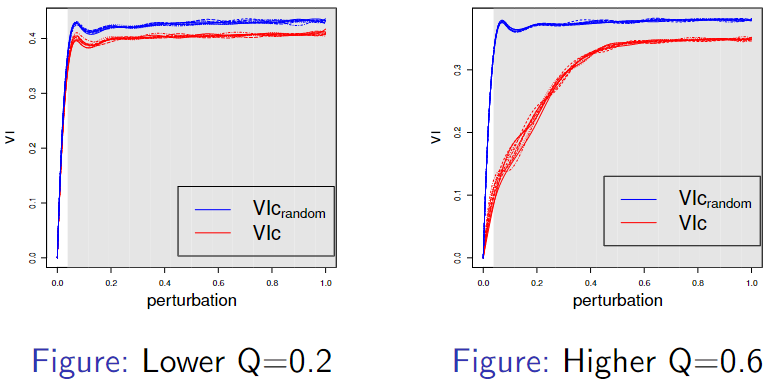
Our Strategy for Weighted Networks

Null Model for Weighted Graphs

Weighted configuration model (WCM) presented in as null random model. An edge of weight w is drawn between two vertices i and j with probability:

 q(w) = pw(1 − p )

 

Perturbation strategy for Weighted Graphs

We propose to use a rewiring approach, which alters a specified number of edges using a series of Bernoulli trials to randomly rewire the network and determines the weight of the new edge between two nodes.

Results on LFN benchmark

and on a set of Real Datasets without ground truth

 

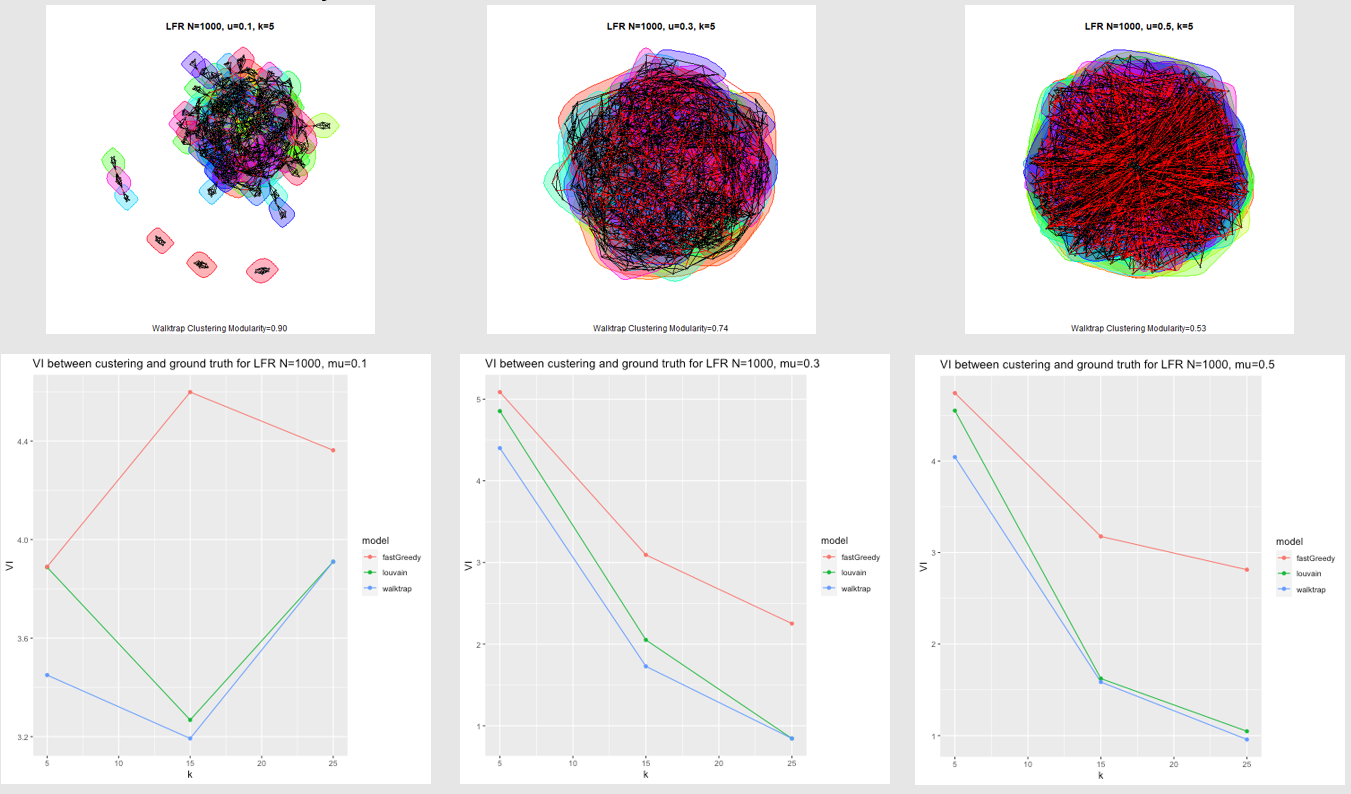
Walktrap most stable results!

Thanks!

References:

[1] Carissimo A., Cutillo L., De Feis I., (2017) Validation of community robustness. Computational Statistics and Data Analysis 120, 1-24
[2] Policastro, V., Righelli, D., Carissimo, A., Cutillo, L., De Feis, I. (2021) R Journal 13:1,292-309
[3] Garlaschelli D. (2009) New Journal of Physics. 11, 073005.
[4] Lancichinetti A., Fortunato S., Radicchi F. (2008) Benchmark graphs for testing community detection algorithms. PHYSICAL REVIEW E 78, 046110

 

IDSAI2023

By Luisa Cutillo

IDSAI2023

  • 129

More from Luisa Cutillo