FUNCTIONAL Nirvana fOR the Object Oriented souls
Rubyconf 2017
Mafinar Khan
panacea systems ltd • product manager • @mafinar
Today We will...
-
Discuss Programming Paradigms
-
Understand Functional Programming
-
Embrace Recursions
-
Grok Immutability
-
Check out some Languages
And Interact along the way...
Programming paradigmS
... what's your kung-fu?
Most of all, differences of opinion are opportunities for learning.
Terry Tempest William


Let's make this structure in our minds...
Focus on Entities
Establish Attributes and Behaviors
Connect Them
Mutate their State through Messages
Make Entities Your Unit
Object Oriented Mindset
Focus on ACTIONS
Apply actions on data
compose and combine actions
transform data
functions are your unit
functional mindset
noun vs verb

//Functional
chases(tom, jerry)// Object Oriented
tom.chases(jerry)Object oriented
- Objects with Attributes and Behaviors
- Mutate through message passing
- Side-effects are okay
- Program as Object Interrelation and Message Passing
Functional
- Lambda Calculus
- Functions in mathematical sense
- Prefer Immutable Data
- Avoid Side Effects and Mutations
- Program as application of functions
Then there's Procedural, Relational, Event Driven, Stack Based and many more...
flex you brain muscles you didn't know existed
understand functional programming
focus thy verbs, not nouns
They've a temper, some of them—particularly verbs: they're the proudest—adjectives you can do anything with, but not verbs—however, I can manage the whole lot of them! Impenetrability! That's what I say!
Humpty Dumpty
just like mathematics
f(x) = sin(x) / cos(x)
Everything is a function
Functions are first class citizen
First Language: 1960
more relevant than ever
Conceived in 1930
Haskell • CommonLisp • Scheme • ML • Erlang • Elixir • Scala • F# • Clojure • Elm • PureScript
Concepts, part i
-
Lambda Calculus
-
Closure
-
Currying and partial functions
-
Higher Order Functions
-
Recursion
lambda calculus
-
Lambda Calculus
- Formal System in Computation
- Based on Function and Application
- Value Binding and Substition
-
1930. alonzo church
-
church turing hypothesis
-
combinators
-
reduction
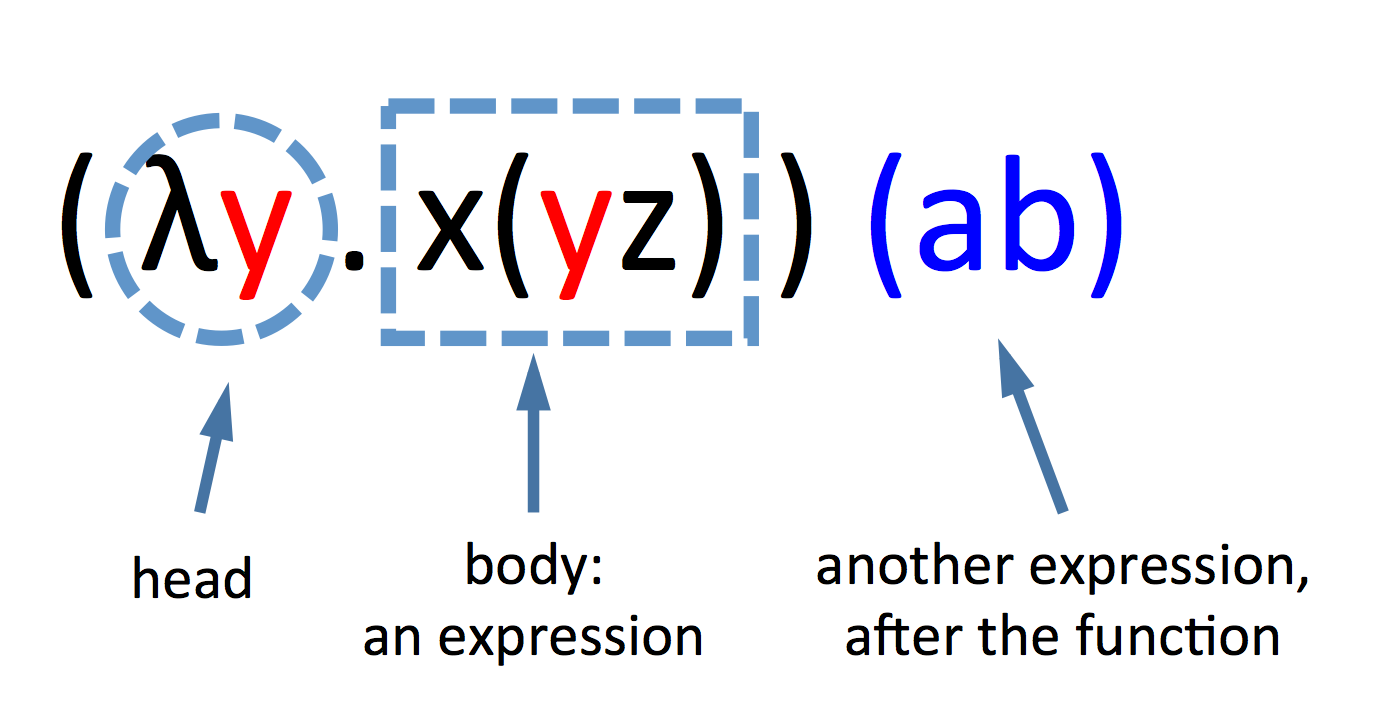
Closures
-
a function that knows its outer scope
-
FUNCTION + ContexT
(def count-up
(let [counter (atom 0)]
(fn [] (do (swap! counter inc) @counter))))
(count-up) ;;=> 1
(count-up) ;;=> 2
(count-up) ;;=> 3- Currying.
- f(x)(y)(z) instead of f(x, y, z)
- Functions take one parameter and return either a closure or output
- Partial Function
- Similar as curried, but applied right away
- partial_application := f(10, y, z)
currying and partial functions
object CurryPartial extends App {
def addCurry(x: Int)(y: Int) = x + y
def increment(who: Int) = addCurry(1, who)
}- A function that-
- Takes one or more functions as argument(s)
- Returns a function
- At least one of the above is true
Higher order functions
(defn sum-of-list [cond-fn]
(fn [apply-fn n]
(->> (range n)
(filter cond-fn)
(map apply-fn)
(reduce +))))
(def sum-of-prime-list (sum-of-list is-prime?)) ; => Prime Number List
(sum-of-prime-list square 100000) ; => Sum of square of primes < 100000recursion
see recursion.
Concepts, part II
-
pure function
-
referencial transparency
-
category theory
pure function
-
Same parameter yields same results
-
no side-effects
-
simpler tests
-
easier memoization
referencial transparency
-
think of a paragraph with no pronouns
-
related to pure functions
-
concurrency
-
Laziness
A mode of containment φ is referentially transparent if, whenever an occurrence of a singular term t is purely referential in a term or sentence ψ(t), it is purely referential also in the containing term or sentence φ(ψ(t)).
embrace recursions
embrace recursions
TO understand recursion, you must first understand recursion
John D. Cook

recursion
-
Function calling itself
-
Needs a terminating condition to end
-
Standard way to loop in functional programming
scala
clojure
def factorial(n: Int): Int = {
if (n == 0)
return 1
else
return n * factorial(n-1)
}
def fib( n : Int) : Int = n match {
case 0 | 1 => n
case _ => fib1( n-1 ) + fib1( n-2 )
}
def sort(a:Array[Int]): Array[Int] =
if (a.length < 2) a
else {
val pivot = a(a.length / 2)
sort (a filter (pivot>)) ++
(a filter (pivot == )) ++
sort (a filter(pivot <))
}(defn fact[x]
(if (<= x 1) 1 (* x (fact (- x 1)))))
(defn fib [n]
(if (< n 2) n (+ (fib (- n 2) (- n 1)))))
(defn quick-sort [[pivot & coll]]
(when pivot
(concat
(quick-sort
(filter #(< % pivot) coll))
[pivot]
(quick-sort
(filter #(>= % pivot) coll)))))Are they efficient?
why do i get stackoverflow?
Tail Call Optimization?
scala
clojure
@annotation.tailrec
def factorial(number: BigInt,
result: BigInt = 1): BigInt = {
if (number == 0) result
else factorial(number -1,
result * number)
}
@annotation.tailrec
def fib( n : Int) : Int = {
def fib_( n: Int,
a:Int,
b:Int): Int = n match {
case 0 => a
case _ => fib_tail( n-1, b, a+b )
}
return fib_( n, 0, 1)
}
(defn fact [x]
(loop [n x f 1]
(if (= n 1)
f
(recur (dec n) (* f n)))))
(defn fib [x, n]
(if (< (count x) n)
(fib (conj x (+ (last x)
(nth x (- (count x) 2)))) n)
x))Recursion in lambda calculus?
Y = λf.(λg.f(gg))(λg.f(gg))
- Fixed Point Functions
- Combinators
grok immutability
and travel times
Choose immutability and see where it takes you
Rich Hickey
travel ±10 years in time...
will it be the same?
Build a new connection.
will you destroy the whole thing and rebuild?

Don't Let time ruin referencial transparency
functional data structure
-
Immutable
-
Structural Sharing
-
Thread Safe
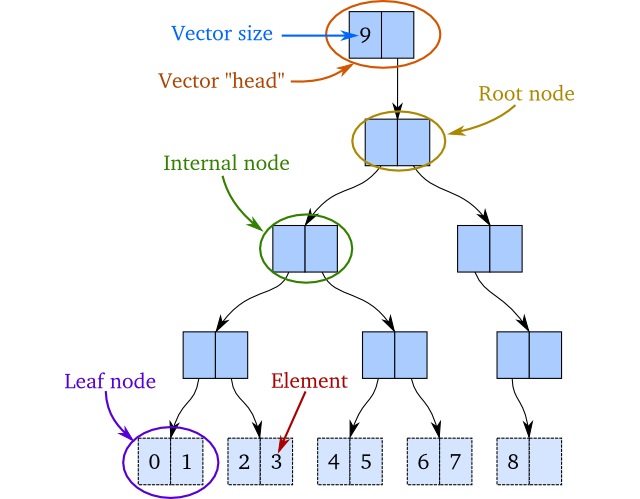
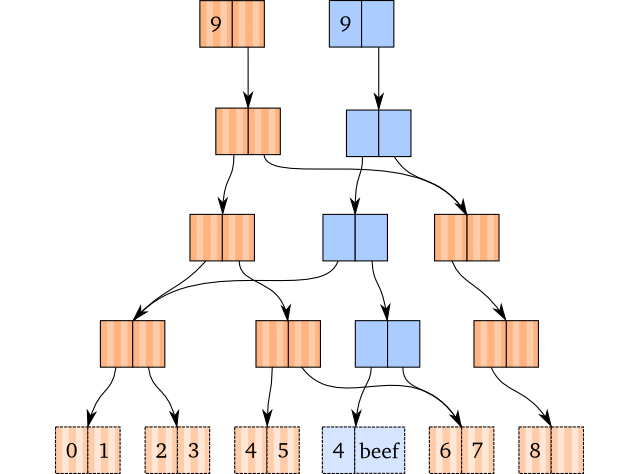
Illustration Time!
It is better to have 100 functions operate on one data structure than 10 functions on 10 data structures
Alan Perlis
Resources and references?
Look no further
sojourner...
-
SICP
-
rich hickey talks
-
Clojure for the Brave and Bold
-
erlang courses in futurelearn
-
Scala Courses in Coursera
-
Thinking Recursively
journeyman...
-
Joy of Clojure
-
Learn you a Haskell for the Great Good
-
Purely Functional Data Structure
master...
-
Lambda Calculus & Combinators
-
Category Theory
-
Advanced Haskell
-
Let Over Lambda
let's talk!!!
FUNCTIONAL NIRVANA FOR THE OBJECT ORIENTED SOULS
By Mafinar Khan
FUNCTIONAL NIRVANA FOR THE OBJECT ORIENTED SOULS
- 1,728



