


\text{Embedding-based Instance Segmentation in Microscopy}
\text{\textbf{Manan Lalit}, Pavel Tomancak, Florian Jug}
\text{Publication}
\text{Project Page}


\text{Instance Segmentation in Bio-Medical Images}

\text{Instance Segmentation in Bio-Medical Images}


\text{Instance Segmentation in Bio-Medical Images}


\text{Instance Segmentation in Bio-Medical Images}



\text{Voxel Grid to Surface Mesh}
\}
\text{Fit dynamic}
\text{models}
\text{Instance Segmentation in Bio-Medical Images}



\text{Voxel Grid to Surface Mesh}
\text{Tracking by Association}

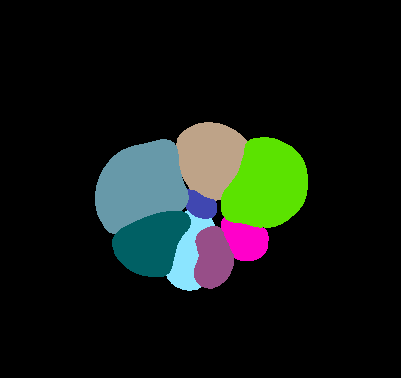
\text{TP* 170}
\text{TP 190}
\text{TP* Time Point}
\}
\text{Fit dynamic}
\text{models}
\}
\text{Instance Segmentation in Bio-Medical Images}



\text{Voxel Grid to Surface Mesh}
\text{Feature-based Registration}
\text{Tracking by Association}
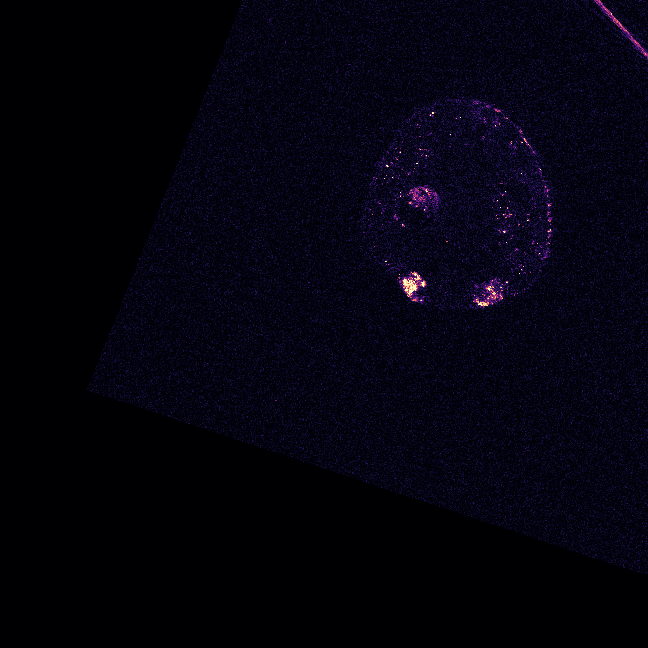
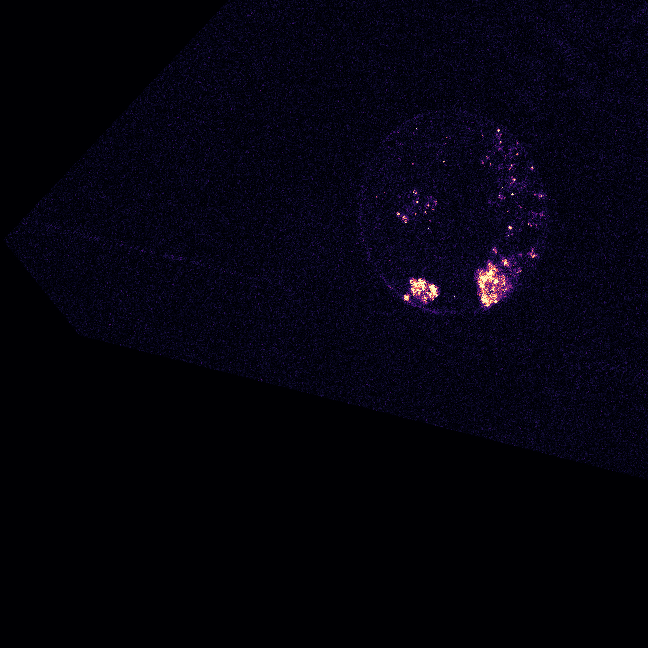
\}
\text{Perform lineage }
\text{tracing}
\}
\text{Evaluate}
\text{curvatures}
\text{Instance Segmentation in Bio-Medical Images}



\text{Voxel Grid to Surface Mesh}
\text{Tracking by Association}


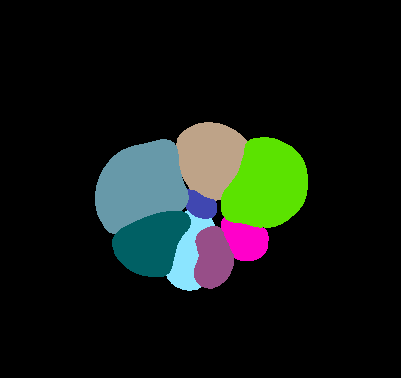
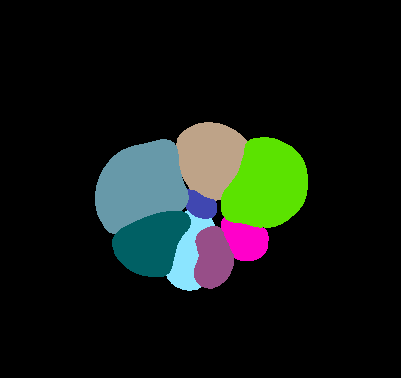
\}
\text{Feature-based Registration}
\text{Perform lineage }
\text{tracing}
\}
\text{Fit dynamic}
\text{models}
\text{Instance Segmentation in Bio-Medical Images}



\text{Voxel Grid to Surface Mesh}
\text{Tracking by Association}


\}
\text{Feature-based Registration}
\text{Perform lineage }
\text{tracing}
\}
\text{Fit dynamic}
\text{models}
\text{Instance Segmentation in Bio-Medical Images}



\text{Voxel Grid to Surface Mesh}
\text{Tracking by Association}
\text{...}


\}
\text{Feature-based Registration}
\text{Align gene}
\text{expression maps}
\text{Perform lineage }
\text{tracing}
\}
\text{Fit dynamic}
\text{models}
\}
\text{Related Work in Bio-Medical Imaging}
\text{StarDist}
\text{Cellpose}
\text{Related Work in Bio-Medical Imaging}
\text{StarDist}

\text{Distance to boundary along \textit{n} rays}
\text{(GT* \textbf{Star Convex} distances)}
\text{``Cell detection with star-convex polygons.", }
\text{``Star-convex Polyhedra for 3D Object Detection \& Segmentation }
\text{in Microscopy.", Weigert and Schmidt et al, WACV, 2020}
\text{Schmidt and Weigert et al, MICCAI, 2018}
\text{*GT: Ground - Truth}

\text{Related Work in Bio-Medical Imaging}


\text{Distance to boundary along \textit{n} rays}
\text{(GT \textbf{Star Convex} distances)}

\text{Normalized Distance Transform}
\text{(GT \textbf{Object probabilities})}
\text{``Cell detection with star-convex polygons.", }
\text{Schmidt and Weigert et al, MICCAI, 2018}
\text{StarDist}
\text{``Star-convex Polyhedra for 3D Object Detection \& Segmentation }
\text{in Microscopy.", Weigert and Schmidt et al, WACV, 2020}
\text{Related Work in Bio-Medical Imaging}
\text{StarDist}

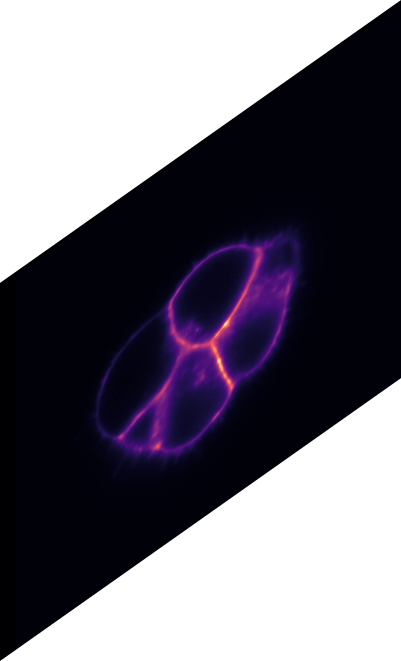












\text{Input}












\text{Target}
\text{\underline{\textit{n}} GT star convex distances }
\text{+ \underline{1} GT object probability }












\text{Related Work in Bio-Medical Imaging}
\text{StarDist}
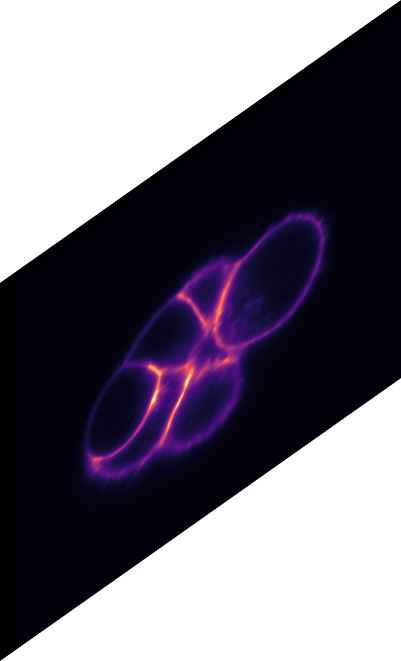













\text{Evaluation Image}
\text{Prediction}













\text{Related Work in Bio-Medical Imaging}
\text{StarDist}


\text{Evaluation Image}













\text{Prediction}
\text{Thresholding on }
\text{Object Probabilities}
\text{+ Greedy NMS*}

\text{*NMS: Non - Maximum Suppression}
\text{Predicted Instance Mask}
\text{Related Work in Bio-Medical Imaging}
\text{StarDist}
\text{Cellpose}
\text{Related Work in Bio-Medical Imaging}
\text{Cellpose}

\frac{\partial^{2}T}{\partial x^{2}} + \frac{\partial^{2}T}{\partial y^{2}} + S = 0
\text{Fourier's steady state heat diffusion equation}
\text{T: temperature}
\text{S: heat source flux}

\text{Stringer et al, Nature Methods, 2020}
\text{``Cellpose: a generalist algorithm for cellular segmentation'', }
\text{Related Work in Bio-Medical Imaging}
\text{Cellpose}



\frac{\partial T}{\partial x}
\frac{\partial T}{\partial y}
\text{(GT*)}
\text{(GT)}
\text{*GT: Ground - Truth}
\text{Stringer et al, Nature Methods, 2020}
\text{``Cellpose: a generalist algorithm for cellular segmentation'', }
\text{Related Work in Bio-Medical Imaging}
\text{Cellpose}














\text{Input}
\text{\underline{2} GT temperature gradient maps }
\text{+ \underline{1} GT binary map }
\text{Target}



\text{Cellpose}

\text{Evaluation Image}
\text{Related Work in Bio-Medical Imaging}



\text{Prediction}













\text{Cellpose}


\text{Related Work in Bio-Medical Imaging}



\text{Thresholding on }
\text{predicted Binary Map }
\text{+ clustering}

\text{Prediction}
\text{Predicted Instance Mask}
\text{Evaluation Image}
\text{(follow the flow)}
\text{Both methods optimize model weights using auxiliary representations}
\text{Both methods \underline{do not} optimize for IoU* metric over GT instance masks}
\text{*IoU: Intersection over Union}
\text{Related Work in the family of Embedding Approaches}
\text{de Brabandere}
\text{and Neven et al, }
\text{2017}
\text{Neven et al,}
\text{2019}
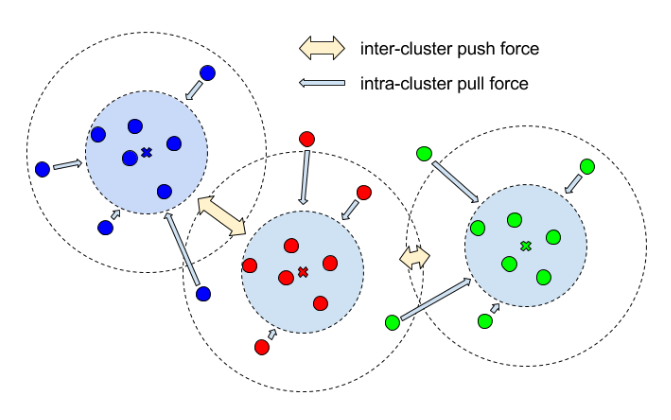
\text{Could we predict a tag or embedding for each pixel such that:}
\text{pixels belonging to same object are clustered together in the embedding space, and}
\text{pixels belonging to different objects are clustered away from each other in }
\text{the embedding space?}
\text{de Brabandere and Neven et al, 2017}
\text{Brabandere and Neven et al, 2017}
\text{``Semantic Instance Segmentation with a Discriminative Loss Function'', }
\text{Related Work in the family of Embedding Approaches}
f_{\theta} (\vec{x}) = \vec{e}
\text{Low level features}
\text{(pixel intensity, position etc)}
\text{High level features }
\text{(high order intensity gradients, }
\text{neighborhood description etc)}
\text{de Brabandere and Neven et al, 2017}
\text{Brabandere and Neven et al, 2017}
\text{``Semantic Instance Segmentation with a Discriminative Loss Function'', }
\text{Related Work in the family of Embedding Approaches}
\text{de Brabandere and Neven et al, 2017}

\text{Brabandere and Neven et al, 2017}
\text{``Semantic Instance Segmentation with a Discriminative Loss Function'', }
\text{intra-cluster variance margin: 0.5 }
\text{inter-cluster distance margin: 1.5 }
\text{also does not optimize for IoU}
\text{Related Work in the family of Embedding Approaches}
\text{embedding} \in \mathcal{R}^{D}
\textbf{+}
\textbf{+}
\textbf{+}
\text{mean instance embedding}
\text{Neven et al, 2019}
\text{and Clustering Bandwidth", Neven et al, 2019}
\text{``Instance Segmentation by Jointly Optimizing Spatial Embeddings }
\text{learn \textit{margin bandwidths} for each pixel}
\text{optimize for IoU metric over target instance masks}
\text{Related Work in the family of Embedding Approaches}
\text{learn a \textit{seediness} score for each pixel}
\text{embedding} \in \mathcal{R}^{D=2}
\text{spatial embedding}
\text{Neven et al, 2019}


















\text{Input}
\text{\textit{offset} to object \textit{center} in x \& y}
\text{Prediction}
\text{\textit{margin bandwidth} in x \& y}
\text{\textit{seediness} score}

\text{Related Work in the family of Embedding Approaches}
\text{Input}


o_{y}
o_{x}
\text{(predicted offset in x)}
\text{(predicted offset in y)}
\text{Related Work in the family of Embedding Approaches}
\text{Loop over each object }
\text{\underline{Step One}: consider offset prediction maps}

\text{Input}

\vec{e} = \vec{x} + \vec{o}
\vec{e}, \vec{x}, \vec{o} \in \mathcal{R}^{2}
\text{.}
\text{.}
\text{.}
\text{.}
\text{.}
\text{.}
\text{.}
\text{.}
\text{Related Work in the family of Embedding Approaches}
\text{Concatenate offsets with pixel positions }
\text{to obtain spatial embeddings }

\text{Input}

\text{Related Work in the family of Embedding Approaches}

\vec{e} = \vec{x} + \vec{o}
\vec{e}, \vec{x}, \vec{o} \in \mathcal{R}^{2}
\text{to obtain spatial embeddings }
\text{Concatenate offsets with pixel positions }
\text{Input}

\text{Related Work in the family of Embedding Approaches}

\overline{\sigma_{x}} = \frac{1}{N}\Sigma_{i} \sigma_{x_{i}}
\text{\underline{Step Two}: Find mean instance margin bandwidth }
\overline{\sigma_{y}} = \frac{1}{N}\Sigma_{i} \sigma_{y_{i}}
\text{Input}

\text{Related Work in the family of Embedding Approaches}

\text{\underline{Step Three}: Compute Gaussian function } \phi
\phi = \mathrm{exp} \left( - \frac{\Vert \vec{e}_{i} - \vec{C} \Vert^{2} }{2 \sigma^{2}}\right)
\text{Related Work in the family of Embedding Approaches}

\phi = \mathrm{exp} \left( - \frac{(e_{ix} - C_{x} )^{2} }{2 \overline{\sigma_{x}}^{2}} - \frac{(e_{iy} - C_{y} )^{2} }{2 \overline{\sigma_{y}}^{2}}\right)

\text{Input}
+
\text{if } \phi(e_{i}) \geq 0.5
\text{pixel at $x_{i}$ is assigned to instance}
\text{\underline{Step Three}: Compute Gaussian function } \phi
\text{Related Work in the family of Embedding Approaches}


\text{Input}
+

\text{Predicted}

\text{GT}
\text{Compute \textit{IoU} between predicted and GT mask}
L_{IoU}
\text{IoU measure in neural networks", Berman et al, CVPR, 2018}
\text{``The lovasz-softmax loss: A tractable surrogate for the optimization of the }
\text{Related Work in the family of Embedding Approaches}

\text{\underline{Step Four}: Compute Seediness Score } s_{i}
L_{\text{seed}} = \Sigma_{i} \Vert s_{i} - \phi(e_{i}) \Vert^{2}

\text{Input}
+
\text{from foreground pixels}
\text{Related Work in the family of Embedding Approaches}

L_{\text{seed}} = \Sigma_{i} \Vert s_{i} - \phi(e_{i}) \Vert^{2}
\text{from foreground pixels}
\text{Regress seediness score from background pixels to 0}
L_{\text{seed}} \mathrel{+}= \Sigma_{i} \Vert s_{i} - 0 \Vert^{2}
\text{\underline{Step Four}: Compute Seediness Score } s_{i}
\text{Related Work in the family of Embedding Approaches}

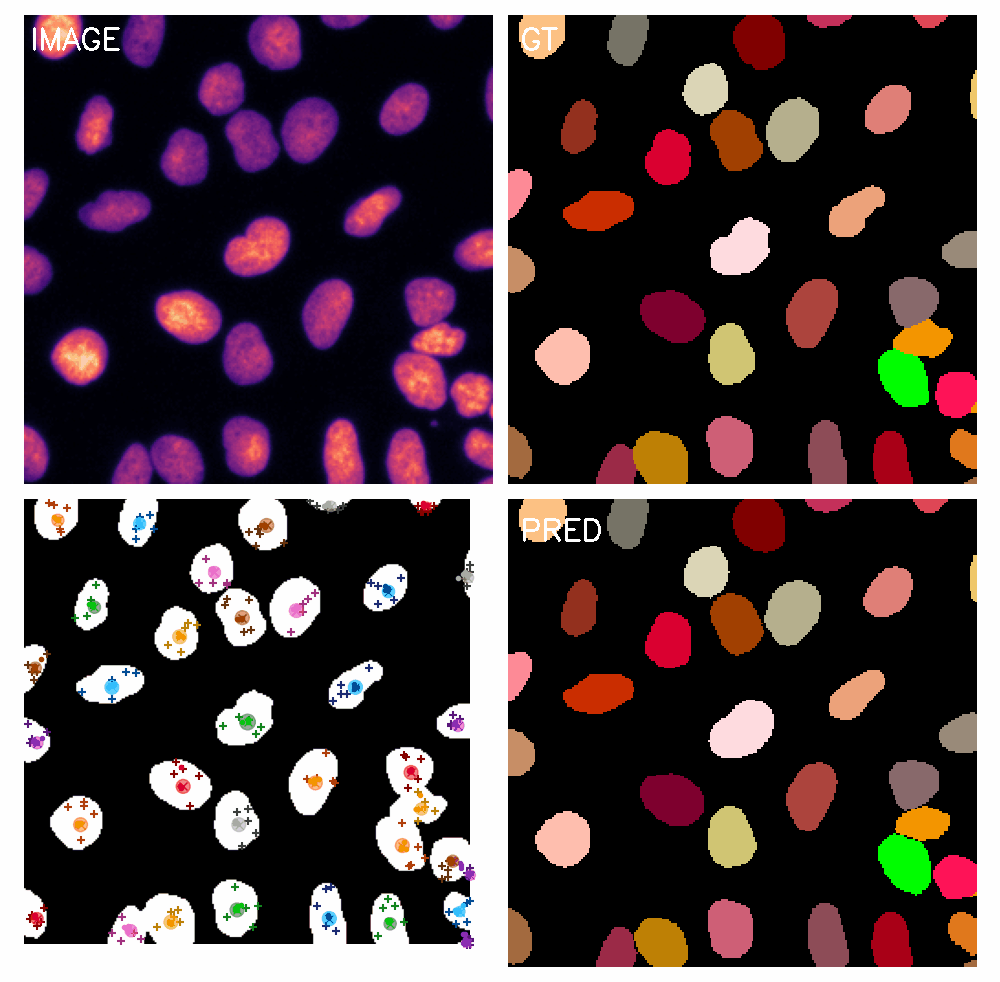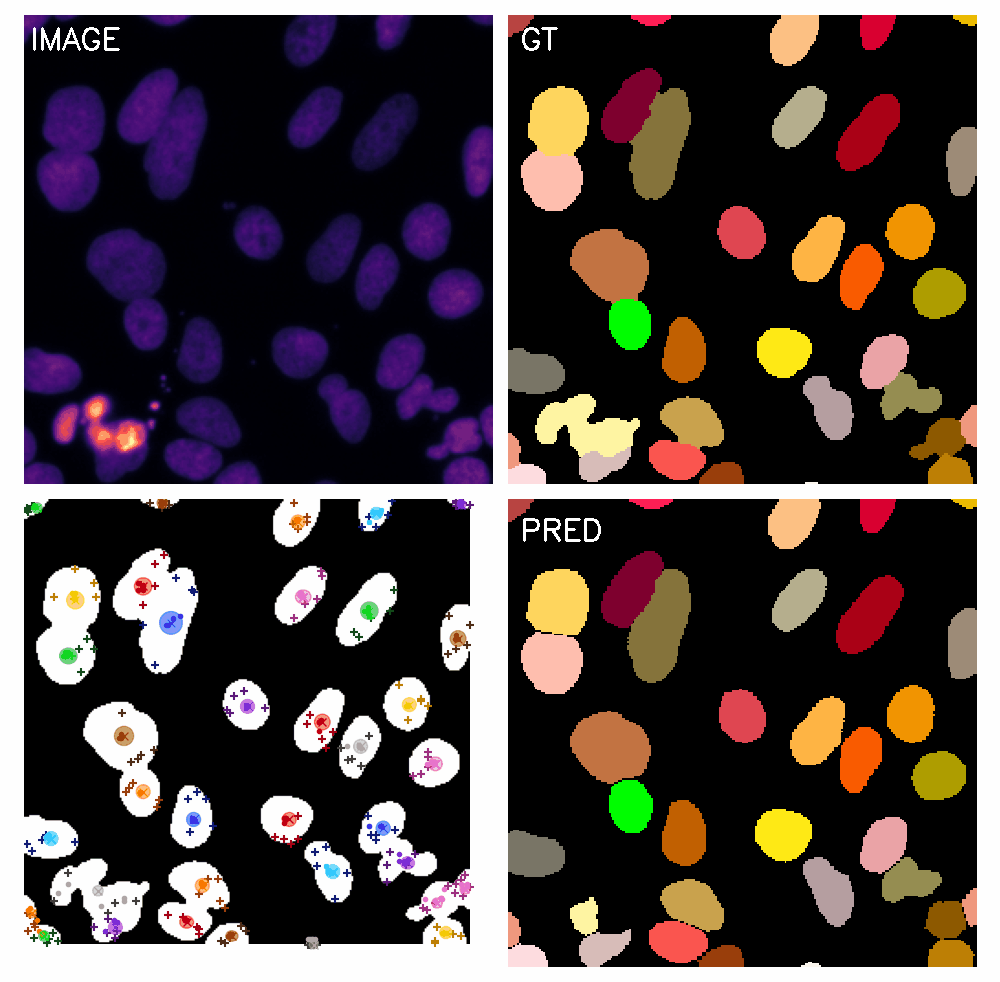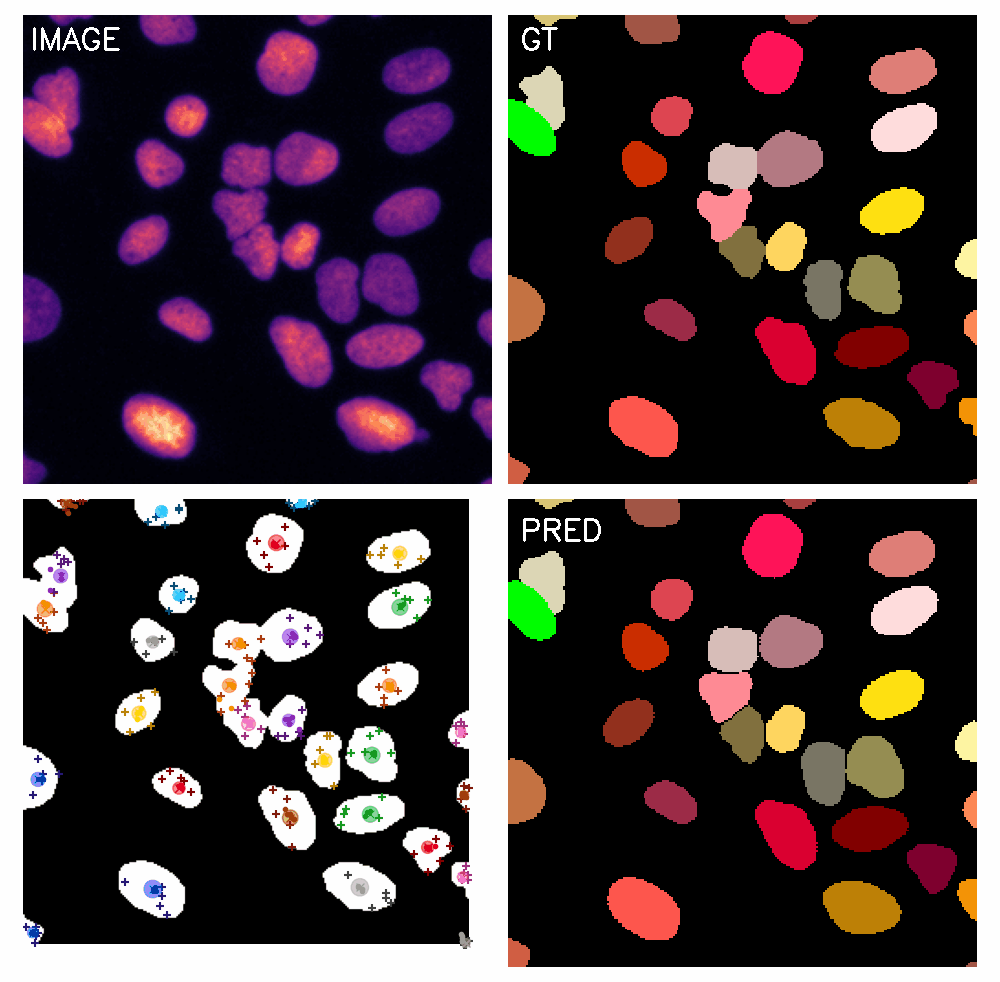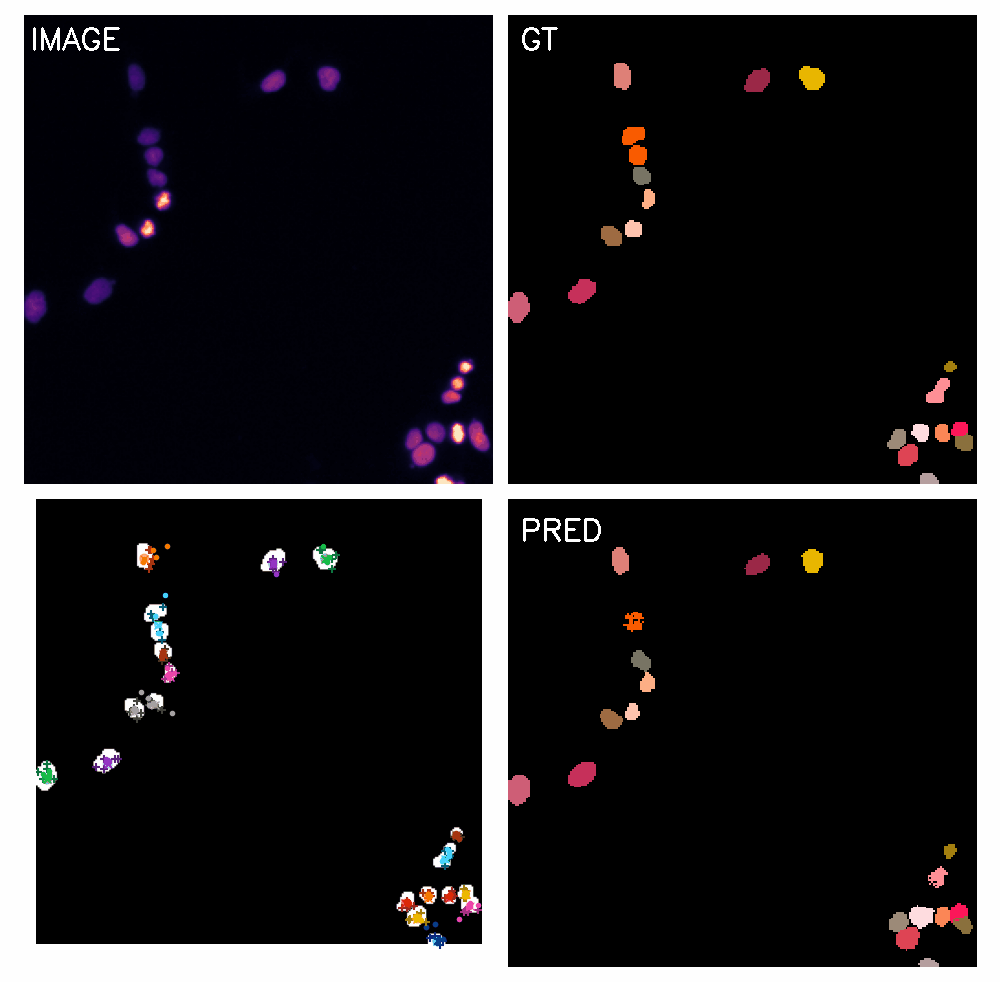
\text{Caicedo et al, Nature Methods 2019" }
\text{``Raw images from BBBC038v1 dataset, }
\text{Neven et al, 2019}
\text{Related Work in the family of Embedding Approaches}


\text{Evaluation Image}












\text{(5 x H x W)}





\text{Neven et al, 2019}
\text{Related Work in the family of Embedding Approaches}


\text{Evaluation Image}
\text{(5 x H x W)}





\text{0.997}
\text{0.995}
\text{0.985}
\text{0.972}
\text{0.963}
\text{0.959}
\text{0.943}
\text{0.929}
\text{0.918}
\text{0.906}
\text{(200, 100)}
\text{(223, 120)}
\text{(130, 260)}
\text{(70, 189)}
\text{(76, 110)}
\text{(105, 67)}
\text{(185, 42)}
\text{(..., ...)}
\text{(..., ...)}
\text{(..., ...)}
\text{Neven et al, 2019}
\text{Related Work in the family of Embedding Approaches}


\text{Evaluation Image}
\text{(5 x H x W)}





\text{0.997}
\text{0.995}
\text{0.985}
\text{0.972}
\text{0.963}
\text{0.959}
\text{0.943}
\text{0.929}
\text{0.918}
\text{0.906}
\text{(200, 100)}
\text{(223, 120)}
\text{(130, 260)}
\text{(70, 189)}
\text{(76, 110)}
\text{(105, 67)}
\text{(185, 42)}
\text{(..., ...)}
\text{(..., ...)}
\text{(..., ...)}
+
\text{Neven et al, 2019}
\text{Related Work in the family of Embedding Approaches}


\text{Evaluation Image}
\text{(5 x H x W)}





\text{0.997}
\text{0.995}
\text{0.985}
\text{0.972}
\text{0.963}
\text{0.959}
\text{0.943}
\text{0.929}
\text{0.918}
\text{0.906}
\text{(200, 100)}
\text{(223, 120)}
\text{(130, 260)}
\text{(70, 189)}
\text{(76, 110)}
\text{(105, 67)}
\text{(185, 42)}
\text{(..., ...)}
\text{(..., ...)}
\text{(..., ...)}
+
\text{For which pixels,}
\phi(e_{i},
+
\text{) > 0.5?}
\text{Neven et al, 2019}
\text{Related Work in the family of Embedding Approaches}


\text{Evaluation Image}
\text{(5 x H x W)}





\text{0.997}
\text{0.995}
\text{0.985}
\text{0.972}
\text{0.963}
\text{0.959}
\text{0.943}
\text{0.929}
\text{0.918}
\text{0.906}
\text{(200, 100)}
\text{(223, 120)}
\text{(130, 260)}
\text{(70, 189)}
\text{(76, 110)}
\text{(105, 67)}
\text{(185, 42)}
\text{(..., ...)}
\text{(..., ...)}
\text{(..., ...)}
+
\text{Neven et al, 2019}
\text{Related Work in the family of Embedding Approaches}


\text{Evaluation Image}
\text{(5 x H x W)}





\text{0.997}
\text{0.995}
\text{0.985}
\text{0.972}
\text{0.963}
\text{0.959}
\text{0.943}
\text{0.929}
\text{0.918}
\text{0.906}
\text{(200, 100)}
\text{(223, 120)}
\text{(130, 260)}
\text{(70, 189)}
\text{(76, 110)}
\text{(105, 67)}
\text{(185, 42)}
\text{(..., ...)}
\text{(..., ...)}
\text{(..., ...)}
+

\text{.}
\text{Choice of GT center}
\text{Choice of GT center}

\text{.}
\text{Choice of GT center}

\text{.}

\text{center = centroid}
\text{predicted instance at inference}
\text{Choice of GT center}

\text{.}
\text{center = medoid}
\text{predicted instance at inference}

\text{Test-time augmentation}

\text{Evaluation Image}
\text{predictions}
\text{(5 x H x W)}

















\text{Test-time augmentation}
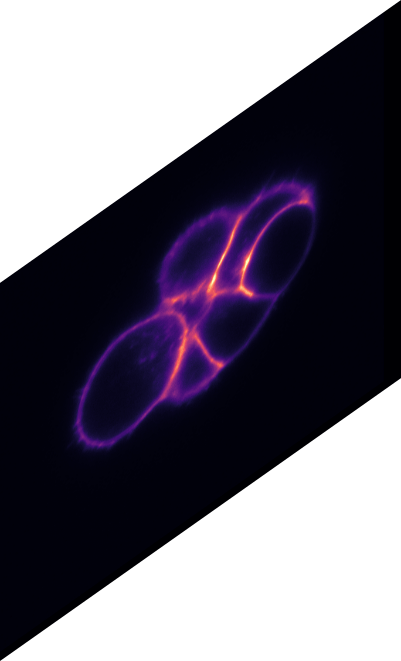
\text{T : rotation transformation by 180 degrees}
T^{-1}(\text{predictions-rotated}) \neq \text{predictions}
\text{T(Evaluation Image)}





\text{(5 x H x W)}
\text{predictions-rotated}












\text{Results - 2d}
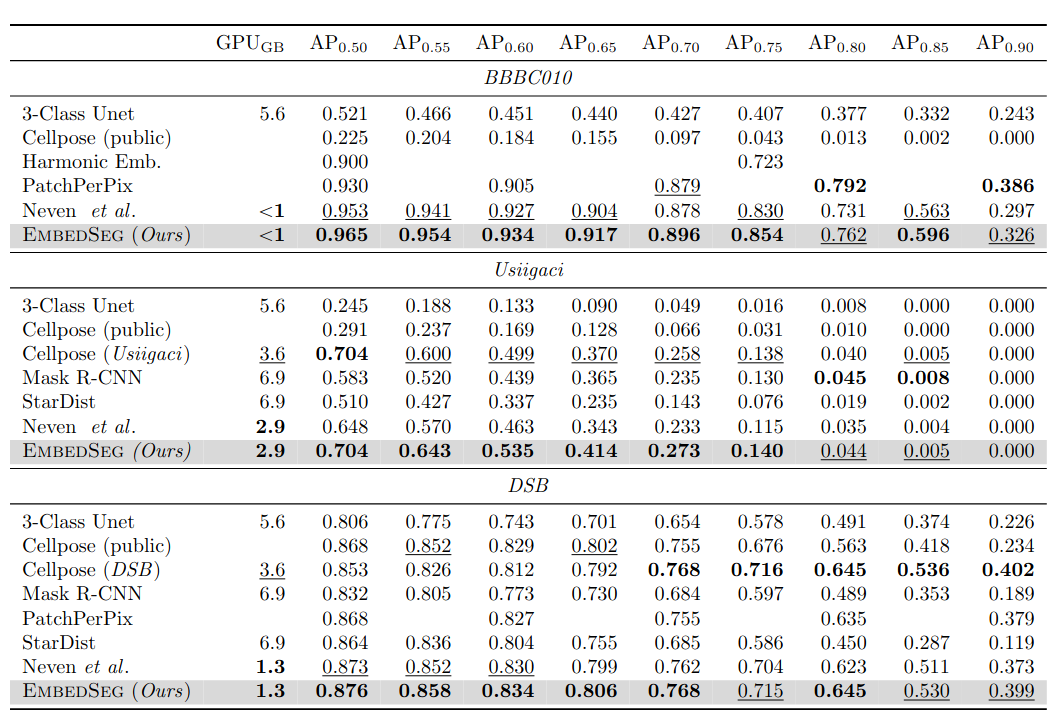


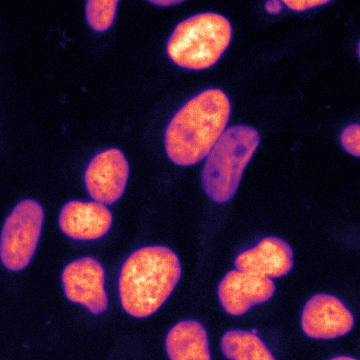
\text{Results - 2d}
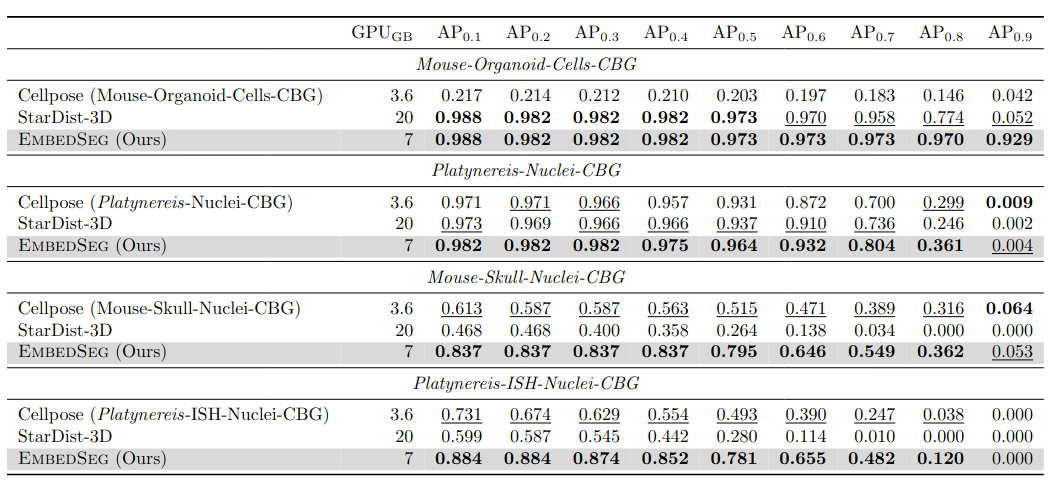
\text{Results - 3d}





\text{Results - 3d}
\text{Qualitative Results}
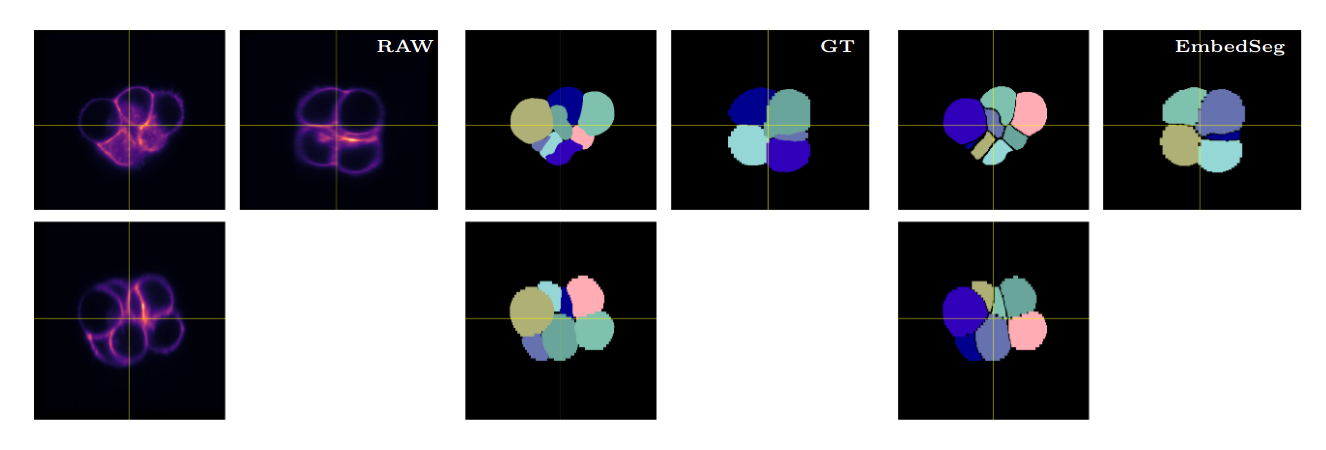
\text{Qualitative Results}
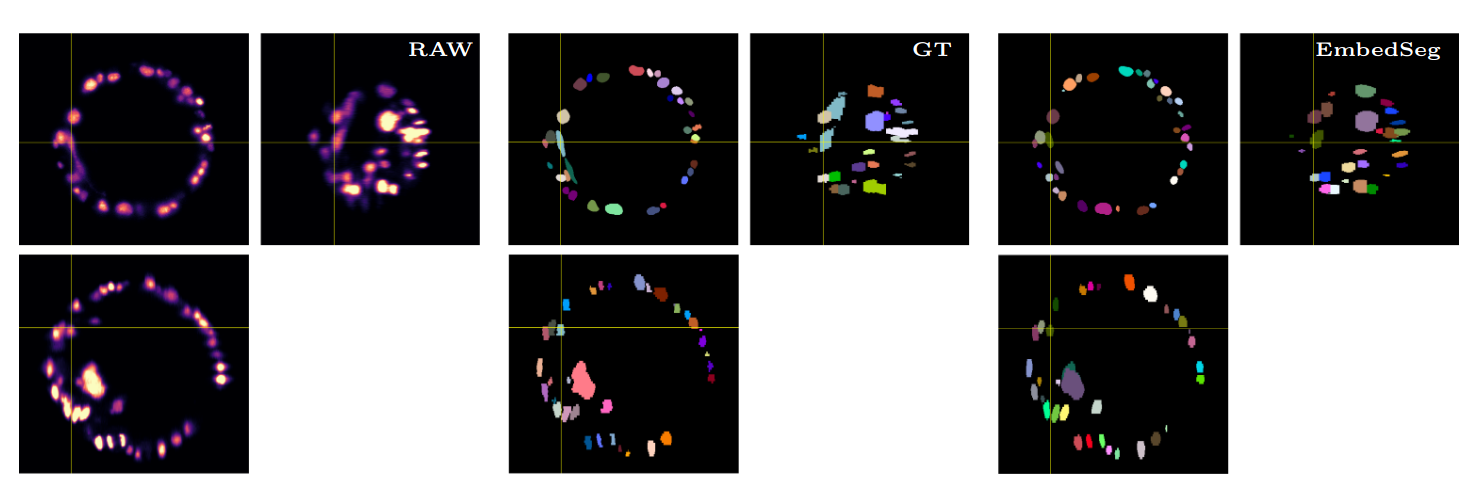
\text{Qualitative Results}
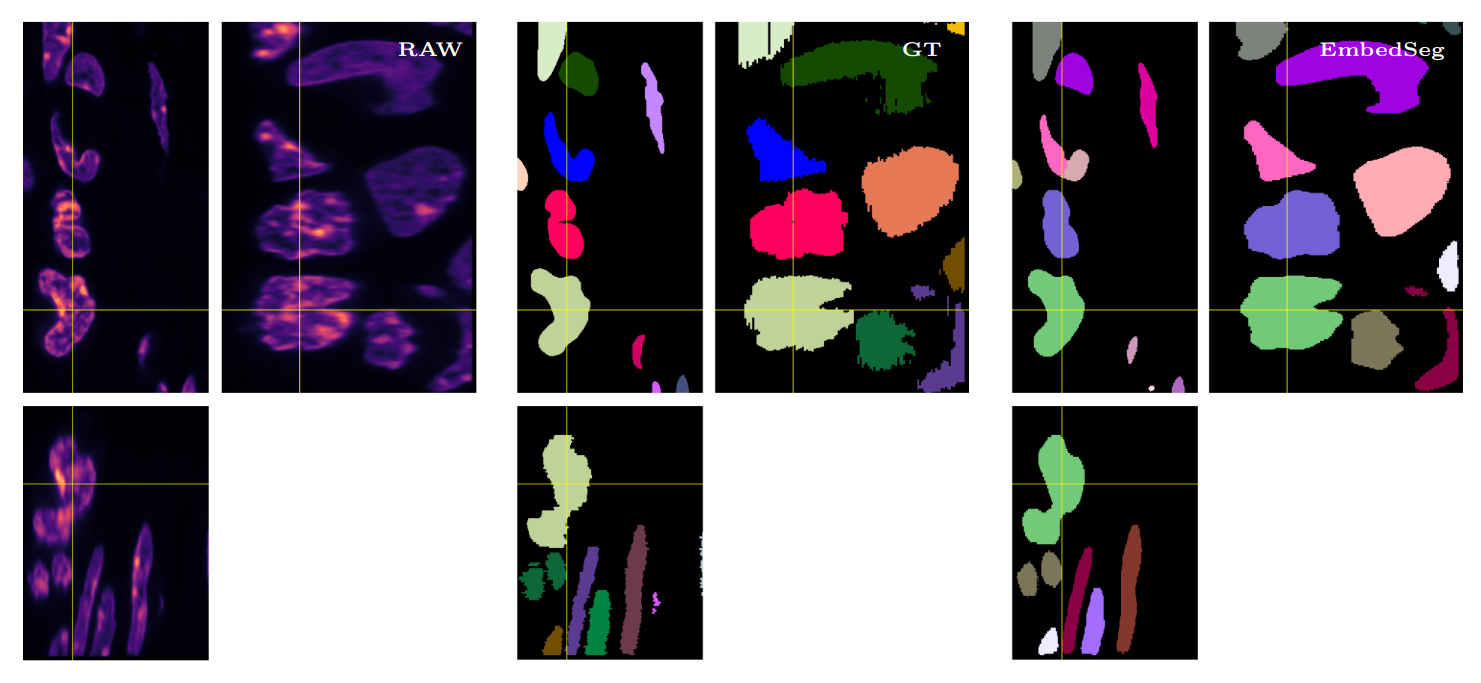
\text{Qualitative Results}

\text{Ablation Studies}
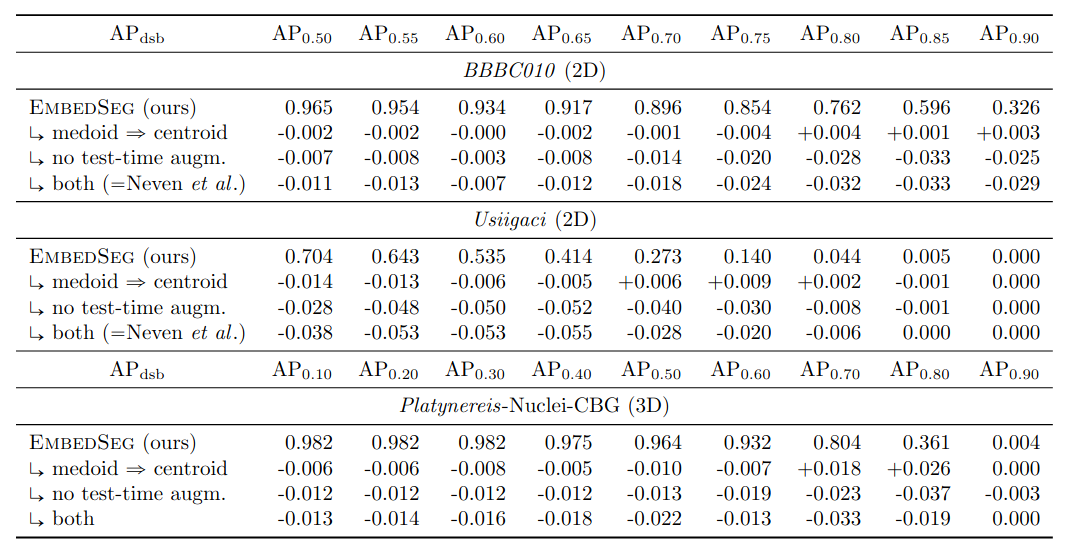
\text{Our Contributions}
\text{Four, new 3d datasets and annotations are made publicly available}

\text{All code and example notebooks are provided}

\text{Demonstrated success of spatial-embedding approaches on biomedical data}

\text{Extended architecture and method to 3d}

\text{Showed that medoid center embedding \& test-time augmentation further boost results}

\text{Our Contributions}
\text{Four, new 3d datasets and annotations are made publicly available}

\text{All code and example notebooks are provided}

\text{Demonstrated success of spatial-embedding approaches on biomedical data}

\text{Extended architecture and method to 3d}

\text{Showed that medoid center embedding \& test-time augmentation further boost results}

\text{https://github.com/juglab/EmbedSeg}

\text{Our Contributions}
\text{Four, new 3d datasets and annotations are made publicly available}

\text{All code and example notebooks are provided}

\text{Demonstrated success of spatial-embedding approaches on biomedical data}

\text{Extended architecture and method to 3d}

\text{Showed that medoid center embedding \& test-time augmentation further boost results}


\text{Provided a light-weight GPU-friendly code which benefits from virtual batching}
\text{Our Contributions}
\text{Four, new 3d datasets and annotations are made publicly available}

\text{All code and example notebooks are provided}

\text{Demonstrated success of spatial-embedding approaches on biomedical data}

\text{Extended architecture and method to 3d}

\text{Showed that medoid center embedding \& test-time augmentation further boost results}

\text{https://github.com/juglab/EmbedSeg-napari}
\text{Provided a light-weight GPU-friendly code which benefits from virtual batching}


















\text{Acknowledgements}
\text{Thank you for listening!}
\newline
\text{Any questions?}
\text{Alex Krull}
\text{Matthias Arzt}
\text{Tim-Oliver Buchholz}
\text{Mangal Prakash}
\text{Anna Goncharova}
\text{Nuno Martins}
\text{Tobias Pietzsch}
\text{Deborah Schmidt}
\text{Florian Jug}
\text{Pavel Tomancak}
\text{Joran Deschamps}
\text{Marina Cuenca}
\text{Giulia Serafini}
\text{Yu-Wen Hsieh}
\text{Bruno Vellutini}
\text{Johannes Girstmair}
\text{Mette Thorsager}

\text{Tom Burke}

\text{Pavel Mejstrik}

\text{Anais Bailles}


MIDL_2021_v4
By Manan Lalit
MIDL_2021_v4
MIDL, 2021 (Long Oral)
- 27


