Breaking of Huygens-Fresnel principle in inhomogeneous Tomonaga-Luttinger liquids
Marek Gluza
presenting based on collaboration with
Spyros Sotiriadis
Per Moosavi
\partial_{t}^{2} \hat{\phi}
= 2 v(x) v'(x) \partial_{x} \hat{\phi}
+ v(x)^2 \partial^2_{x} \hat{\phi}
\partial_{t}^{2} \hat{\phi}
= v(x)v'(x) \partial_{x} \hat{\phi}
+ v(x)^2\partial^2_{x} \hat{\phi}
\mapsto
NTU Singapore
Huygens-Fresnel principle
What would it mean Huygens-Fresnel principle is broken?
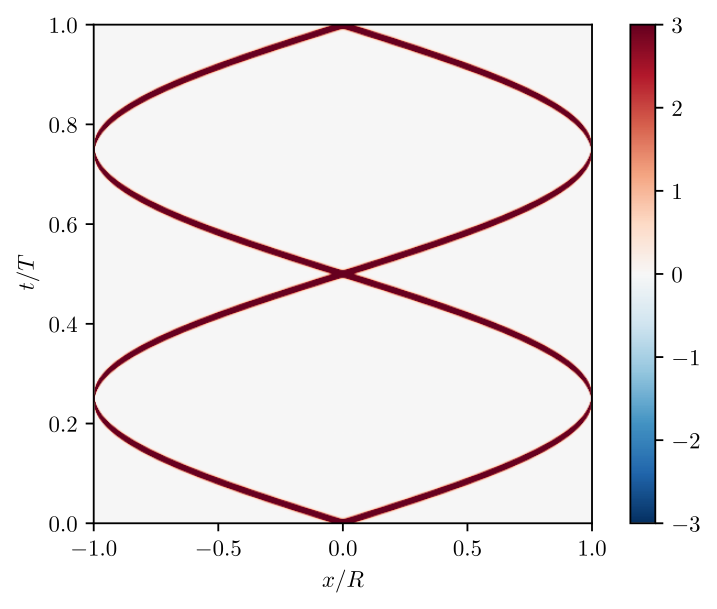
Wave-front propagation
pinned to light-cone
Wave-front leaking into light-cone
(x,t) \mapsto (\xi,\tau)
Is Huygens-Fresnel principle valid for quantum fluids?
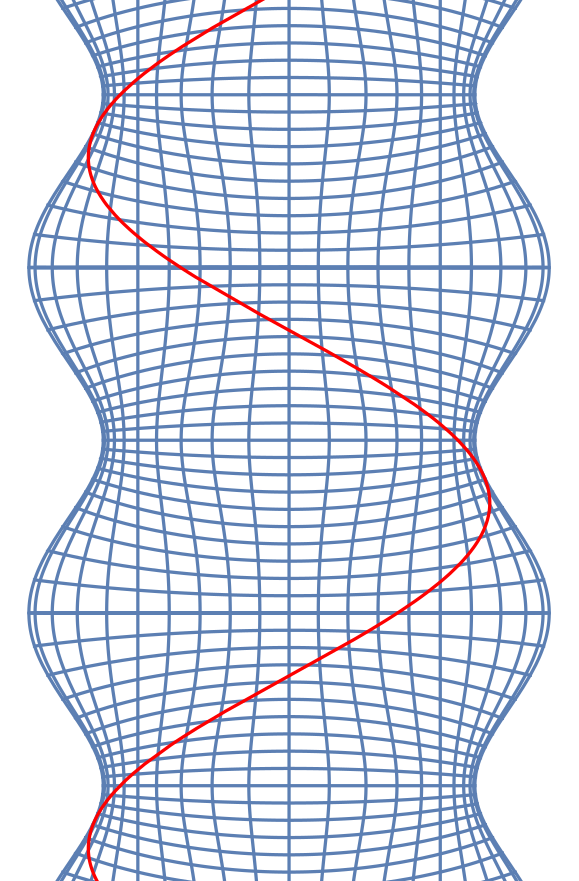
The light-cone can be curved
(x,t) \mapsto (\xi,\tau)
Our contribution:
Is Huygens-Fresnel principle valid for quantum fluids?
\hat H_\text{TLL}
= \int_{0}^{L} \mathrm{d}x\,v_\text{S}
\biggl(
K \partial_{x} \hat{\phi}(x)^2
+ {K}^{-1}\partial_{t} \hat{\phi}(x)^2
\biggr)
Tomonaga-Luttinger liquid
Tomonaga-Luttinger liquid
Out-of-equilibrium phenomenology
H
= \frac{1}{2} \int_{-R}^{R} \mathrm{d}x\,
\biggl(
\frac{v(x)}{K(x)} \pi (x)^2
+ v(x)K(x) [\partial_{x} \hat{\phi}(x)]^2
+ (M v_0)^2 v(x)K(x) \hat{\phi}(x)^2
\biggr)
\hat H_\text{TLL}
= \int_{0}^{L} \mathrm{d}x\,v_\text{S}
\biggl(
K \partial_{x} \hat{\phi}(x)^2
+ {K}^{-1}\partial_{t} \hat{\phi}(x)^2
\biggr)
hydrodynamics
Local signals stay local
Local signals propagate
with constant velocity
Local signals return
to the origin
#Simple
Quantum field refrigerators in the TLL model:
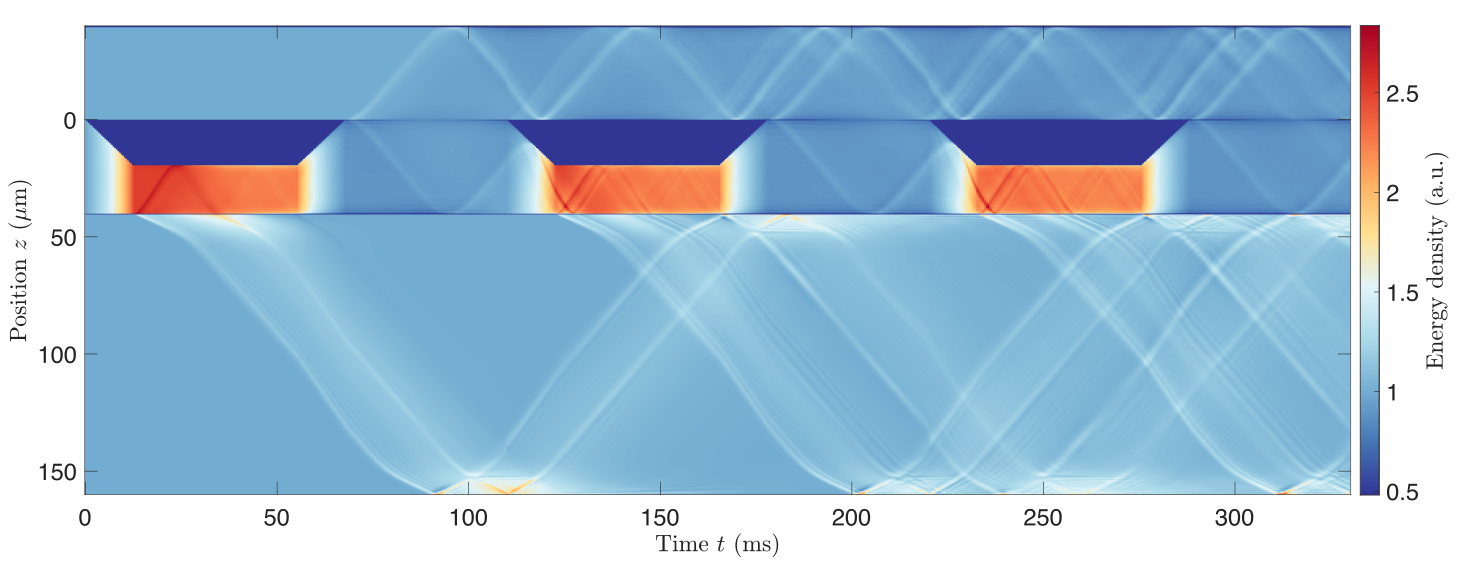
System
Piston
Bath
Bath with excitations
System cooled down
Tomonaga-Luttinger liquid
Inhomogeneous
\hat H
= \int_{0}^{L} \mathrm{d}x\,v(x)
\biggl(
{K(x)}^{-1} \hat\pi (x)^2
+ K(x) \partial_{x} \hat{\phi}(x)^2
\biggr)
\hat H
= \int_{0}^{L} \mathrm{d}x\,v(x)
\biggl(
{K}^{-1} \hat\pi (x)^2
+ K \partial_{x} \hat{\phi}(x)^2
\biggr)
\hat H_\text{TLL}
= \int_{0}^{L} \mathrm{d}x\,v_\text{S}
\biggl(
K \partial_{x} \hat{\phi}(x)^2
+ {K}^{-1}\partial_{t} \hat{\phi}(x)^2
\biggr)
Tomonaga-Luttinger liquid
Inhomogeneous
\hat H
= \int_{0}^{L} \mathrm{d}x\,v(x)
\biggl(
{K(x)}^{-1} \hat\pi (x)^2
+ K(x) \partial_{x} \hat{\phi}(x)^2
\biggr)
Tomonaga-Luttinger liquid
Inhomogeneous
Local signals stay local?
Local signals propagate
with constant velocity?
Local signals return
to the origin?
#Complex
Out-of-equilibrium phenomenology
Energy of phonons
E
E
E
E
hydrodynamics
Tomonaga-Luttinger liquid
Cold atoms as
\hat H_\text{TLL} = \int_0^L \text{d}x\biggl( \frac{\hbar^2n_{GP}}{2m}\partial_x\hat\varphi^2+g\delta\hat\varrho^2\biggr)
\delta\varrho
\partial_z\varphi
\partial_z\varphi
\ll
\delta\varrho
\ll
\hat H_\text{TLL}
= \int_{0}^{L} \mathrm{d}x\,v_\text{S}
\biggl(
K \partial_{x} \hat{\phi}(x)^2
+ {K}^{-1}\partial_{t} \hat{\phi}(x)^2
\biggr)
What if: The atom density will not be constant?
Tomonaga-Luttinger liquid
Cold atoms as
Tomonaga-Luttinger liquid
Cold atoms as
an inhomogeneous
\hat H_\text{TLL} = \int_0^L \text{d}x\biggl( \frac{\hbar^2n_{GP}}{2m}\partial_x\hat\varphi^2+g\delta\hat\varrho^2\biggr)
\delta\varrho
\partial_z\varphi
\partial_z\varphi
\ll
\delta\varrho
\ll
\hat H_\text{TLL}
= \int_{0}^{L} \mathrm{d}x\,v_\text{S}
\biggl(
K \partial_{x} \hat{\phi}(x)^2
+ {K}^{-1}\partial_{t} \hat{\phi}(x)^2
\biggr)
\hat H
= \int_{0}^{L} \mathrm{d}x\,v(x)
\biggl(
{K(x)}^{-1} \hat\pi (x)^2
+ K(x) \partial_{x} \hat{\phi}(x)^2
\biggr)
n_\text{GP}(x)
{K(x)}
v(x)
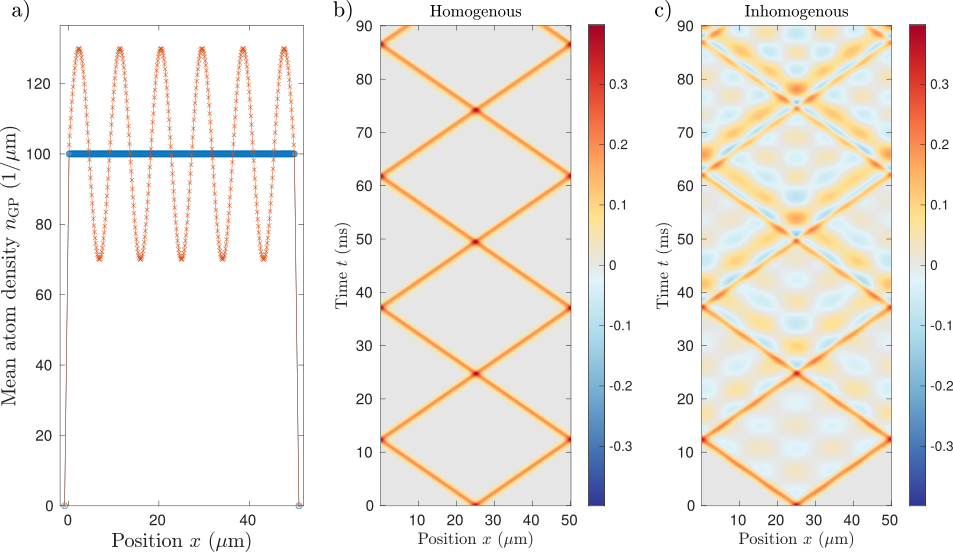
Huygens-Fresnel principle
Huygens-Fresnel principle broken
Tomonaga-Luttinger liquid
Cold atoms as
an inhomogeneous
\hat H_\text{TLL} = \int_0^L \text{d}x\biggl( \frac{\hbar^2n_{GP}}{2m}\partial_x\hat\varphi^2+g\delta\hat\varrho^2\biggr)
\delta\varrho
\partial_z\varphi
\partial_z\varphi
\ll
\delta\varrho
\ll
\hat H_\text{TLL}
= \int_{0}^{L} \mathrm{d}x\,v_\text{S}
\biggl(
K \partial_{x} \hat{\phi}(x)^2
+ {K}^{-1}\partial_{t} \hat{\phi}(x)^2
\biggr)
\hat H
= \int_{0}^{L} \mathrm{d}x\,v(x)
\biggl(
{K(x)}^{-1} \hat\pi (x)^2
+ K(x) \partial_{x} \hat{\phi}(x)^2
\biggr)
n_\text{GP}(x)
{K(x)}
v(x)
Huygens-Fresnel principle
Huygens-Fresnel principle broken
\partial_{t}^{2} \hat{\phi}
= 2 v(x) v'(x) \partial_{x} \hat{\phi}
+ v(x)^2 \partial^2_{x} \hat{\phi}
\partial_{t}^{2} \hat{\phi}
= v(x)v'(x) \partial_{x} \hat{\phi}
+ v(x)^2\partial^2_{x} \hat{\phi}
\mapsto
Breaking of Huygens-Fresnel principle in inhomogeneous Tomonaga-Luttinger liquids
Marek Gluza
Spyros Sotiriadis
Per Moosavi
\partial_{t}^{2} \hat{\phi}
= 2 v(x) v'(x) \partial_{x} \hat{\phi}
+ v(x)^2 \partial^2_{x} \hat{\phi}
\partial_{t}^{2} \hat{\phi}
= v(x)v'(x) \partial_{x} \hat{\phi}
+ v(x)^2\partial^2_{x} \hat{\phi}
\mapsto
NTU Singapore
Breaking of Huygens-Fresnel principle in inhomogeneous Tomonaga-Luttinger liquids
By Marek Gluza
