Lecture:
Quantum
compiling
Marek Gluza
NTU Singapore
slides.com/marekgluza
*Background explanation: It's a primitive bricklayer!
What is our quantum computer?
What is a universal quantum computer?
∣ψ⟩=a∣0⟩+b∣1⟩
|\psi\rangle = a | 0 \rangle + b | 1\rangle
∣ψ⟩=a∣00⟩+b∣10⟩+c∣01⟩+b∣11⟩
|\psi\rangle = a | 00 \rangle + b | 10\rangle+c | 01 \rangle + b | 11\rangle
∣ψ⟩=a∣000⟩+b∣100⟩+c∣010⟩+d∣100⟩+e∣011⟩+f∣101⟩+g∣110⟩+h∣111⟩
|\psi\rangle = a | 000 \rangle + b | 100\rangle+c | 010 \rangle + d | 100\rangle+
e | 011 \rangle + f | 101\rangle+g | 110 \rangle +h | 111\rangle
∣ψ⟩=a∣0000⟩+b∣1000⟩+c∣0100⟩+d∣1000⟩+e∣0011⟩+f∣0101⟩+g∣1010⟩+h∣1100⟩+…
|\psi\rangle = a | 0000 \rangle + b | 1000\rangle+c | 0100 \rangle + d | 1000\rangle+
e | 0011 \rangle + f | 0101\rangle+g | 1010 \rangle +h | 1100\rangle + \ldots
1 qubit
2 qubits
3 qubits
4 qubits
And you get the idea lah
∣ψ⟩=U∣00…0⟩⇒U≈Uc
|\psi\rangle = U |00\ldots0\rangle \Rightarrow U \approx U_c
we will approximate via circuits
It's all about the group of unitary matrices
U(n)={M∈Cn×n:M−1=M†}
U(n) = \{ M\in \mathbb C^{n\times n}: M^{-1} = M^\dagger\}
M,M′∈U(n)⇒(MM′)(MM′)†=MM′(M′)†M†
M,M' \in U(n) \Rightarrow (M M')(MM')^\dagger = M M'(M')^\dagger M^\dagger
=MM†=I
= M M^\dagger = I
M,M′∈U(n)⇒MM′∈U(n)
M,M' \in U(n) \Rightarrow M M'\in U(n)
M∈U(n)⇒∃H:M=eiH
M \in U(n) \Rightarrow \exist H: M = e^{i H}
What is a quantum algorithm?
\hat H \mapsto \hat \mathcal H_\ell = \hat \mathcal U_\ell^\dagger \hat H \hat\mathcal U_\ell
\partial_\ell \hat \mathcal H_\ell = [[A(\hat \mathcal H_\ell),B(\hat \mathcal H_\ell)], \hat \mathcal H_\ell]
0
0
0
0
C
What is a quantum computer?
It's an experimental setup A which includes a quantum system B and that setup A allows to manipulate the quantum state of B.
What is a quantum algorithm?
0
0
0
0
C
What is a universal quantum computer?
It's an experimental setup which includes a quantum system and that setup allows to manipulate its quantum state.
It's an experimental setup which includes few-level quantum systems and that setup allows to manipulate the quantum state using gates.
These gates form a universal gate set which means that if you apply sufficiently many you will be able to reach any desired quantum state.
What are quantum gates?
∣ψ⟩=a∣0⟩+b∣1⟩
|\psi\rangle = a | 0 \rangle + b | 1\rangle
∣+⟩=21(∣0⟩+∣1⟩)
|+\rangle = \frac 1 {\sqrt 2} (| 0 \rangle + | 1\rangle)
What are quantum gates?
∣ψ⟩=∣0⟩
|\psi\rangle = | 0 \rangle
Z∣0⟩=∣0⟩
Z|0\rangle = | 0\rangle
Z∣μ⟩=(−1)μ∣μ⟩
Z|\mu\rangle = (-1)^\mu| \mu\rangle
Useful notation
Exercise: By evaluating the determinant, prove that it's impossible to apply Z in the lab
What are quantum gates?
∣ψ⟩=∣0⟩
|\psi\rangle = | 0 \rangle
∣+⟩=21(∣0⟩+∣1⟩)
|+\rangle = \frac 1 {\sqrt 2} (| 0 \rangle + | 1\rangle)
Use the quantum computer to transform
into
Trivial quantum algorithm solves it:
Apply the Haddamard gate
H=21(111−1)
H = \frac 1 {\sqrt 2} \begin{pmatrix} 1 & 1 \\ 1 &- 1\end{pmatrix}
0
H
H
What are all single qubit quantum gates?
What are 2 qubit quantum gates?
∣ψ⟩=∣0⟩⊗∣0⟩
|\psi\rangle = | 0 \rangle \otimes |0\rangle
∣+⟩⊗∣+⟩=21(∣00⟩+∣01⟩+∣10⟩+∣11⟩)
|+\rangle \otimes |+\rangle = \frac 1 { 2} (| 0 0\rangle + | 01\rangle+|10\rangle + | 11\rangle)
Use the quantum computer to transform
into
Apply the Haddamard gate on each qubit
H⊗H
H\otimes H
0
H
H
0
H
H
What are quantum gates?
∣ψ⟩=∣0⟩⊗∣0⟩
|\psi\rangle = | 0 \rangle \otimes |0\rangle
∣Φ⟩=21(∣00⟩+∣11⟩)
|\Phi\rangle = \frac 1 { \sqrt 2} (| 0 0\rangle + | 11\rangle)
Use the quantum computer to transform
into
Apply the Haddamard gate on each qubit
H⊗1
H\otimes 1
and then apply the controlled-not gate
CNOT=∣0⟩⟨0∣⊗1+∣1⟩⟨1∣⊗X
\text{CNOT} = |0\rangle\langle 0|\otimes 1 + |1\rangle\langle1 |\otimes X
H
H
0
0
+
+
Universal gate set "Ising + single qubit"
gXX(t)=e−itXiXi+1
g_{XX}(t) = e^{-it X_iX_{i+1} }
gX(i)=e−itXi
g_X(i) = e^{-itX_i}
gZ(i)=e−itZi
g_Z(i) = e^{-itZ_i }
0
0
0
0
Universal gate set #2
CZ
CZ
gX=e−itXi
g_X = e^{-itX_i}
gZ=e−itZi
g_Z = e^{-itZ_i }
=100001000010000−1
= \begin{pmatrix} 1 & 0 &0 & 0\\ 0& 1 &0 & 0\\ 0&0&1&0 \\ 0&0&0 &- 1\end{pmatrix}
Universal gate set #3: Surface code
CZ
CZ
Ti=e−iπ/4Xi
T_i = e^{-i\pi/4 X_i}
Zi
Z_i
=100001000010000−1
= \begin{pmatrix} 1 & 0 &0 & 0\\ 0& 1 &0 & 0\\ 0&0&1&0 \\ 0&0&0 &- 1\end{pmatrix}
Xi
X_i
About CZ
I⊗Z=10000−1000010000−1
I\otimes Z = \begin{pmatrix} 1 & 0 &0 & 0\\ 0& -1 &0 & 0\\ 0&0&1&0 \\ 0&0&0 &- 1\end{pmatrix}
Z⊗I=1000010000−10000−1
Z\otimes I = \begin{pmatrix} 1 & 0 &0 & 0\\ 0& 1 &0 & 0\\ 0&0&-1&0 \\ 0&0&0 &- 1\end{pmatrix}
Z⊗Z=10000−10000−100001
Z\otimes Z = \begin{pmatrix} 1 & 0 &0 & 0\\ 0& -1 &0 & 0\\ 0&0&-1&0 \\ 0&0&0 & 1\end{pmatrix}
About CZ
I⊗Z=10000−1000010000−1
I\otimes Z = \begin{pmatrix} 1 & 0 &0 & 0\\ 0& -1 &0 & 0\\ 0&0&1&0 \\ 0&0&0 &- 1\end{pmatrix}
Z⊗I=1000010000−10000−1
Z\otimes I = \begin{pmatrix} 1 & 0 &0 & 0\\ 0& 1 &0 & 0\\ 0&0&-1&0 \\ 0&0&0 &- 1\end{pmatrix}
Z⊗Z=10000−10000−100001
Z\otimes Z = \begin{pmatrix} 1 & 0 &0 & 0\\ 0& -1 &0 & 0\\ 0&0&-1&0 \\ 0&0&0 & 1\end{pmatrix}
2I⊗I−Z⊗I−I⊗Z+Z⊗Z=100001000010000−1
2 I\otimes I -Z\otimes I- I\otimes Z + Z\otimes Z = \begin{pmatrix} 1 & 0 &0 & 0\\ 0& 1 &0 & 0\\ 0&0&1&0 \\ 0&0&0 &- 1\end{pmatrix}
Exercise: derive this using the Hilbert-Schmidt scalar product.
Implementing CZ
CZ=ei2π(Z⊗I+I⊗Z−Z⊗Z)
\text{CZ} = e^{i \frac \pi 2 ( Z\otimes I + I\otimes Z - Z\otimes Z)}
gXX(t)=e−itXiXi+1
g_{XX}(t) = e^{-it X_iX_{i+1} }
gX(i)=e−itXi
g_X(i) = e^{-itX_i}
gZ(i)=e−itZi
g_Z(i) = e^{-itZ_i }
0
0
0
0
Exercise: Use commutation relations and BCH formula to implement CZ with the Ising gate set
All 2 qubit operations
CNOT
CNOT
gX=e−itXi
g_X = e^{-itX_i}
gZ=e−itZi
g_Z = e^{-itZ_i }
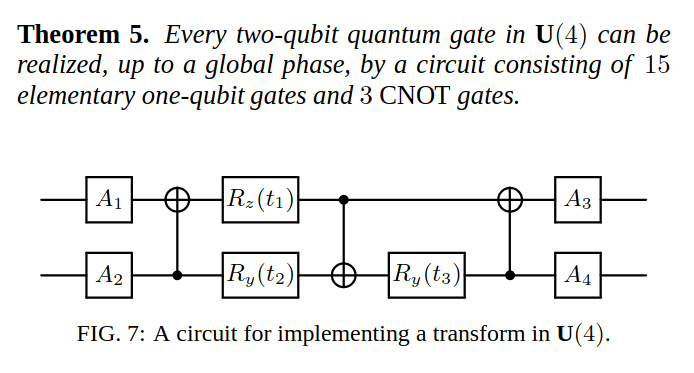
About CNOT
+
CNOT=∣0⟩⟨0∣⊗1+∣1⟩⟨1∣⊗X
\text{CNOT} = |0\rangle\langle 0|\otimes 1 + |1\rangle\langle1 |\otimes X
CZ=∣0⟩⟨0∣⊗1+∣1⟩⟨1∣⊗Z
\text{CZ} = |0\rangle\langle 0|\otimes 1 + |1\rangle\langle1 |\otimes Z
=100001000010000−1
= \begin{pmatrix} 1 & 0 &0 & 0\\ 0& 1 &0 & 0\\ 0&0&1&0 \\ 0&0&0 &- 1\end{pmatrix}
=(1⊗H)CNOT(1⊗H)
= (1\otimes H) CNOT (1\otimes H)
Swap gate from CNOT
SWAP=1000001001000001
SWAP = \begin{bmatrix} 1&0&0&0\\0&0&1&0\\0&1&0&0\\0&0&0&1\end{bmatrix}
SWAP=2I⊗I+X⊗X+Y⊗Y+Z⊗Z
SWAP=\frac{I\otimes I +X\otimes X+Y\otimes Y+Z\otimes Z}{2}
Universality is generic:
Universal gate set "Ising + single qubit"
gXX(t)=e−itXiXi+1
g_{XX}(t) = e^{-it X_iX_{i+1} }
gX(i)=e−itXi
g_X(i) = e^{-itX_i}
gZ(i)=e−itZi
g_Z(i) = e^{-itZ_i }
0
0
0
0
How can we use it to implement any unitary?
Universal quantum computation
How can we use it to implement any unitary?
U(n)={M∈Cn×n:M−1=M†}
U(n) = \{ M\in \mathbb C^{n\times n}: M^{-1} = M^\dagger\}
SU(n)={M∈U(n):det(M)=1}
SU(n) = \{ M\in U(n): det(M)=1\}
={exp(iH):H=H†,tr(H)=0}
= \{ exp(i H): H=H^\dagger, tr(H)=0\}
Implement its Hamiltonian
Implementing Hamiltonians
H=μ,ν∈{0,1}×L∑⟨Z(μ)X(ν),H⟩Z(μ)X(ν)
H = \sum_{\mu,\nu\in\{0,1\}^{\times L}} \langle Z(\mu)X(\nu),H\rangle Z(\mu)X(\nu)
H+H′=H†+(H′)†=(H+H′)†
H + H' = H^\dagger +(H')^\dagger =(H +H')^\dagger
Hermitian matrices are a vector space
Wμ,ν=Z(μ)X(ν)
W_{\mu,\nu} = Z(\mu)X(\nu)
Is a basis
Orthonormal
expansion
In the exam* you will prove
Wμ,ν=Z(μ)X(ν)
W_{\mu,\nu} = Z(\mu)X(\nu)
Is a basis
Z(μ)=⊗k=1L(σz)μk
Z(\mu) =\otimes_{k=1}^L(\sigma^z)^{\mu_k}
X(ν)=⊗k=1L(σx)νk
X(\nu) =\otimes_{k=1}^L(\sigma^x)^{\nu_k}
How to get
Zi=I⊗(i−1)σz⊗IL−i
Z_i =I^{\otimes (i-1)} \sigma^z\otimes I^{L-i}
ei=(0,0,…1@i,0…)
e_i= (0,0,\ldots 1 @ i, 0\ldots)
Z(ei)=Zi
Z(e_i) = Z_i
* This is super important, so what if it was on some exam? Could you prove it?
In the exam you will prove
Wμ,ν=Z(μ)X(ν)
W_{\mu,\nu} = Z(\mu)X(\nu)
Is a basis
Z(μ)=⊗k=1L(σz)μk
Z(\mu) =\otimes_{k=1}^L(\sigma^z)^{\mu_k}
X(ν)=⊗k=1L(σx)νk
X(\nu) =\otimes_{k=1}^L(\sigma^x)^{\nu_k}
How to get
Yi=I⊗(i−1)σy⊗IL−i
Y_i =I^{\otimes (i-1)} \sigma^y\otimes I^{L-i}
ei=(0,0,…1@i,0…)
e_i= (0,0,\ldots 1 @ i, 0\ldots)
Z(ei)X(ei)∝Yi
Z(e_i)X(e_i) \propto Y_i
Universal quantum computation
SU(n)={exp(iH):H=H†,tr(H)=0}
SU(n) = \{ exp(i H): H=H^\dagger, tr(H)=0\}
H=μ,ν∈{0,1}×L∑⟨Z(μ)X(ν),H⟩Z(μ)X(ν)
H = \sum_{\mu,\nu\in\{0,1\}^{\times L}} \langle Z(\mu)X(\nu),H\rangle Z(\mu)X(\nu)
H=μ,ν∈{0,1}×L∑Hμ,νZ(μ)X(ν)
H = \sum_{\mu,\nu\in\{0,1\}^{\times L}}H_{\mu,\nu} Z(\mu)X(\nu)
Universal quantum computation
SU(n)={exp(iH):H=H†,tr(H)=0}
SU(n) = \{ exp(i H): H=H^\dagger, tr(H)=0\}
H=μ,ν∈{0,1}×L∑Hμ,νZ(μ)X(ν)
H = \sum_{\mu,\nu\in\{0,1\}^{\times L}}H_{\mu,\nu} Z(\mu)X(\nu)
U=eitH≡eiH′
U=e^{it H} \equiv e^{i H'}
U=eitH=μ,ν∈{0,1}×L∏eiHμ,νZ(μ)X(ν)
U=e^{it H} \neq \left( \prod_{\mu,\nu\in\{0,1\}^{\times L}}e^{iH_{\mu,\nu} Z(\mu)X(\nu)}\right )
Trotter-Suzuki decomposition
H^TFIM=∑i=1L−1XiXi+1+∑i=1LZi≡H^X+H^Z
\hat H_\text{TFIM} = \sum_{i=1}^{L-1}X_iX_{i+1}+\sum_{i=1}^L Z_i\\
\equiv \hat H_X +\hat H_Z
∣ψ(t)⟩=e−itH^TFIM∣0⟩⊗L
|\psi(t)\rangle = e^{-it \hat H_\text{TFIM}}{|0\rangle}^{\otimes L}
∣ψ(t)⟩=(e−iNtH^Xe−iNtH^Z)N∣0⟩⊗L+E^∣0⟩⊗L
|\psi(t)\rangle = \left(e^{-i\frac tN \hat H_X}e^{-i\frac tN \hat H_Z}\right)^N{|0\rangle}^{\otimes L} + \hat E{|0\rangle}^{\otimes L}
gXX(t)=e−itXiXi+1
g_{XX}(t) = e^{-it X_iX_{i+1} }
gX(i)=e−itXi
g_X(i) = e^{-itX_i}
gZ(i)=e−itZi
g_Z(i) = e^{-itZ_i }
0
0
0
0
Trotter-Suzuki decomposition
∥E^∥=∥e−it(H^X+H^Z)−(e−iNtH^Xe−iNtH^Z)N∥
\|\hat E\| = \|e^{-it(\hat H_X +\hat H_Z)} - \left(e^{-i\frac tN \hat H_X}e^{-i\frac tN \hat H_Z}\right)^N\|
≤Nt2∥[H^X,H^Z]∥
\le \frac{t^2}N\|[\hat H_X,\hat H_Z]\|
Why does it work?
BCH formula
e−it(H^X+H^Z)=e−itH^Xe−itH^Ze−i2t2[H^X,H^Z]…
e^{-it( \hat H_X +\hat H_Z)}=e^{-it\hat H_X }e^{-it\hat H_Z}e^{-i\frac {t^2}2[\hat H_X ,\hat H_Z]}\ldots
∥1−e−i2t2[H^X,H^Z]∥≤2t2∥[H^X,H^Z]∥
\|\mathbb 1 - e^{-i\frac {t^2}2[\hat H_X ,\hat H_Z]}\| \le \frac {t^2}2 \|[ \hat H_X ,\hat H_Z]\|
Conclusion: For short evolution time we're happy
How to implement Trotter-Suzuki?
e−itH^X=∏i=1L−1e−itXiXi+1
e^{-it\hat H_X}=\prod_{i=1}^{L-1}e^{-it X_iX_{i+1} }
gX(i)=e−itXiXi+1
g_X(i) = e^{-itX_i X_{i+1}}
gZ(i)=e−itZi
g_Z(i) = e^{-itZ_i }
Use Solovay-Kitaev algorithm to compile these gates but usually they are the primitive gates
(e−iNtH^Xe−iNtH^Z)N∣0⟩⊗L
(e^{-i\frac tN \hat H_X}e^{-i\frac tN \hat H_Z})^N{|0\rangle}^{\otimes L}
0
0
0
0
Exercise: Local error bound
Qx=ei(1−x)Aei(1−x)Beix(A+B)
Q_x = e^{i(1-x)A}e^{i(1-x)B}e^{ix(A+B)}
Q1=ei(A+B)
Q_1 = e^{i(A+B)}
Q0=eiAeiB
Q_0 = e^{i A}e^{i B}
∂xQx=ei(1−x)A(−A−B+AB+B)ei(1−x)Beix(A+B)
\partial_x Q_x = e^{i(1-x)A}\left(-A-B+ A_B+B\right)e^{i(1-x)B} e^{ix(A+B)}
AB=ei(1−x)BAe−i(1−x)B=A+ieiξxB[A,B]e−iξxB
A_B = e^{i(1-x)B}A e^{-i(1-x)B} = A + i e^{i\xi_x B}[A,B] e^{-i\xi_x B}
∥Q0−Q1∥=∥∫01dx∂xQx∥=∥[A,B]∥
\|Q_0-Q_1\| =\| \int_0^1 dx \partial_x Q_x\| = \|[A,B]\|
Exercise: Non-commutative identity
Xm−Ym=∑j=0m−1Xm−1−j(X−Y)Yj
X^m - Y^m = \sum_{j=0}^{m-1}X^{m-1-j}(X-Y)Y^j
≤∑j=0N−1∥e−i(N−1−j)NtH^X(e−iNtH^X−e−iNtH^Z)e−ijNtH^Z∥
\le \sum_{j=0}^{N-1}\|e^{-i (N-1-j)\frac tN \hat H_X}(e^{-i\frac tN \hat H_X}-e^{-i\frac tN \hat H_Z})e^{-ij\frac tN \hat H_Z}\|
∥e−it(H^X+H^Z)−(e−iNtH^Xe−iNtH^Z)N∥
\|e^{-it(\hat H_X +\hat H_Z)} - \left(e^{-i\frac tN \hat H_X}e^{-i\frac tN \hat H_Z}\right)^N\|
≤∑j=0N−1∥e−iNtH^X−e−iNtH^Z∥≤Nt2∥[HX,HZ]∥
\le \sum_{j=0}^{N-1}\|e^{-i \frac tN \hat H_X}-e^{-i\frac tN \hat H_Z}\| \le \frac{t^2}N \|[H_X,H_Z]\|
cf.:
xm−ym=(x−y)∑j=0m−1xm−1−jyj
x^m -y ^m = (x-y)\sum_{j=0}^{m-1}x^{m-1-j}y^j
Application to physics:
Universal quantum computation
SU(n)={exp(iH):H=H†,tr(H)=0}
SU(n) = \{ exp(i H): H=H^\dagger, tr(H)=0\}
H=μ,ν∈{0,1}×L∑Hμ,νZ(μ)X(ν)
H = \sum_{\mu,\nu\in\{0,1\}^{\times L}}H_{\mu,\nu} Z(\mu)X(\nu)
U=eitH=μ,ν∈{0,1}×L∏eiHμ,νZ(μ)X(ν)
U=e^{it H} \neq \left( \prod_{\mu,\nu\in\{0,1\}^{\times L}}e^{iH_{\mu,\nu} Z(\mu)X(\nu)}\right )
U=eitH=N→∞limμ,ν∈{0,1}×L∏eiN1Hμ,νZ(μ)X(ν)N
U=e^{it H} = \lim_{N\rightarrow \infty} \left( \prod_{\mu,\nu\in\{0,1\}^{\times L}}e^{i\frac 1N H_{\mu,\nu} Z(\mu)X(\nu)}\right )^N
Constructive quantum compilation
SU(n)={exp(iH):H=H†,tr(H)=0}
SU(n) = \{ exp(i H): H=H^\dagger, tr(H)=0\}
H=μ,ν∈{0,1}×L∑Hμ,νZ(μ)X(ν)
H = \sum_{\mu,\nu\in\{0,1\}^{\times L}}H_{\mu,\nu} Z(\mu)X(\nu)
U=eitH=N→∞limμ,ν∈{0,1}×L∏eiN1Hμ,νZ(μ)X(ν)N
U=e^{it H} = \lim_{N\rightarrow \infty} \left( \prod_{\mu,\nu\in\{0,1\}^{\times L}}e^{i\frac 1N H_{\mu,\nu} Z(\mu)X(\nu)}\right )^N
How to get
Clifford circuits
Wμ,ν=Z(μ)X(ν)
W_{\mu,\nu} = Z(\mu)X(\nu)
For every
There exists
Cμ,ν∈U(n)
C_{\mu,\nu} \in U(n)
Such that
Cμ,νWμ,νCμ,ν†=Z1
C_{\mu,\nu} W_{\mu,\nu} C_{\mu,\nu}^\dagger= Z_1
Super crucial exam formula
H′=UHU†
H' = UHU^\dagger
eiH′=UeiHU†
e^{iH'} = Ue^{iH}U^\dagger
⇒
\Rightarrow
Cμ,ν∈U(n)
C_{\mu,\nu} \in U(n)
Cμ,νWμ,νCμ,ν†=Z1
C_{\mu,\nu} W_{\mu,\nu} C_{\mu,\nu}^\dagger= Z_1
U∈U(n)
U \in U(n)
Super crucial exclam formula
⇒
\Rightarrow
eiWμ,ν′=Cμ,ν†eiZ1Cμ,ν
e^{iW_{\mu,\nu}'} =C_{\mu,\nu}^\dagger e^{iZ_1}C_{\mu,\nu}
Super cool exciting formula
U=eitH=N→∞limμ,ν∈{0,1}×L∏eiN1Hμ,νZ(μ)X(ν)N
U=e^{it H} = \lim_{N\rightarrow \infty} \left( \prod_{\mu,\nu\in\{0,1\}^{\times L}}e^{i\frac 1N H_{\mu,\nu} Z(\mu)X(\nu)}\right )^N
U=eitH=N→∞limμ,ν∈{0,1}×L∏Cμ,ν†eiN1Hμ,νZ1Cμ,νN
U=e^{it H} = \lim_{N\rightarrow \infty} \left( \prod_{\mu,\nu\in\{0,1\}^{\times L}}C_{\mu,\nu}^\dagger e^{i\frac 1 N H_{\mu,\nu}Z_1}C_{\mu,\nu}\right )^N
Super cool exclam formula
U=eitH=N→∞limμ,ν∈{0,1}×L∏Cμ,ν†eiN1Hμ,νσz⊗I⊗L−1Cμ,νN
U=e^{it H} = \lim_{N\rightarrow \infty} \left( \prod_{\mu,\nu\in\{0,1\}^{\times L}}C_{\mu,\nu}^\dagger e^{i\frac 1 N H_{\mu,\nu}\sigma^z}\otimes I^{\otimes L-1}C_{\mu,\nu}\right )^N
In this (insane) model: all we ever do is make infinitesimally small rotations on qubit 1 and then distribute that onto all the other qubits using Clifford operations
Surely, there must be better ways?!
Addendum: Clifford circuits
Wμ,ν=Z(μ)X(ν)
W_{\mu,\nu} = Z(\mu)X(\nu)
For every
There exists
Cμ,ν∈U(n)
C_{\mu,\nu} \in U(n)
Such that
Cμ,νWμ,νCμ,ν†=Z1
C_{\mu,\nu} W_{\mu,\nu} C_{\mu,\nu}^\dagger= Z_1
Addendum: formal definition Clifford circuits
Wμ,ν,q=qZ(μ)X(ν)
W_{\mu,\nu,q} = q Z(\mu)X(\nu)
Wμ,ν,qWμ′,ν′,q=q′′Z(μ′′)X(ν′′)=Wμ′′,ν′′,q′′
W_{\mu,\nu,q} W_{\mu',\nu',q}= q'' Z(\mu'')X(\nu'')=W_{\mu'',\nu'',q''}
This is called the Pauli group
P(L)
\mathcal P(L)
Addendum: formal definition Clifford circuits
Wμ,ν,q=qZ(μ)X(ν)
W_{\mu,\nu,q} = q Z(\mu)X(\nu)
Pauli operators have essentially the same spectrum
Z(μ)=⊗k=1L(σz)μk
Z(\mu) =\otimes_{k=1}^L(\sigma^z)^{\mu_k}
X(ν)=⊗k=1L(σx)νk
X(\nu) =\otimes_{k=1}^L(\sigma^x)^{\nu_k}
Z(μ)∣μ⟩=⊗Zμk∣μk⟩=⊗(−1)μk∣μk⟩
Z(\mu)|\mu\rangle = \otimes Z^{\mu_k}|\mu_k\rangle= \otimes (-1)^{\mu_k}|\mu_k\rangle
X(μ)∣μ⟩+=⊗Xμk∣μk⟩+=⊗(−1)μk∣μk⟩+
X(\mu)|\mu\rangle_+ = \otimes X^{\mu_k}|\mu_k\rangle_+= \otimes (-1)^{\mu_k}|\mu_k\rangle_+
There must be unitary operators mapping them to each other
Uμ,ν,q†Wμ,ν,qUμ,ν,qWμ′,ν′,q
U_{\mu,\nu,q}^\dagger W_{\mu,\nu,q} U_{\mu,\nu,q} W_{\mu',\nu',q}
Addendum: formal definition Clifford circuits
Wμ,ν,q=qZ(μ)X(ν)
W_{\mu,\nu,q} = q Z(\mu)X(\nu)
C(L)={U∈U(L) s.t. UP(L)U†=P(L)}
C(L) = \{ U\in U(L) \text{ s.t. } U\mathcal P(L)U^\dagger = \mathcal P(L)\}
All you need is single qubit and CNOTs
U=eitH=N→∞limμ,ν∈{0,1}×L∏Cμ,ν†eiN1Hμ,νσz⊗I⊗L−1Cμ,νN
U=e^{it H} = \lim_{N\rightarrow \infty} \left( \prod_{\mu,\nu\in\{0,1\}^{\times L}}C_{\mu,\nu}^\dagger e^{i\frac 1 N H_{\mu,\nu}\sigma^z}\otimes I^{\otimes L-1}C_{\mu,\nu}\right )^N
∣ψ(t)⟩=e−itH^∣ψ(0)⟩
|\psi(t)\rangle = e^{-it \hat H}|\psi(0)\rangle
How to compute it on a laptop?
How to compute it on a quantum computer?
Hamiltonian simulation
∣ψ(t)⟩=e−itH^∣ψ(0)⟩
|\psi(t)\rangle = e^{-it \hat H}|\psi(0)\rangle
How to compute it on a laptop?
For qubits, your laptop can do ~13 spins at finite temperature and ~25 spins for a pure state (use sparsity)
(10)⊗(10)=1000
\begin{pmatrix}1\\0\end{pmatrix}\otimes \begin{pmatrix}1\\0\end{pmatrix} = \begin{pmatrix}1\\0\\0\\0\end{pmatrix}
At the end of the day:
Workarounds:
Hamiltonian simulation
∣ψ(t)⟩=e−itH^∣ψ(0)⟩
|\psi(t)\rangle = e^{-it \hat H}|\psi(0)\rangle
How to compute it on a quantum computer?
Use quantum algorithms 'Hamiltonian simulation'
Trotter-Suzuki
Linear combination of unitaries
Qubitization
Randomized compiler
Hamiltonian simulation
Truncated series
P: Runs easily
BPP: Often runs easily
BQP: Often quantums easily
NP: Optimizes easily
QMA
P: Runs easily
BPP: Often runs easily
BQP: Often quantums easily
NP: Optimizes easily
Key idea for post-Trotter methods
C(U,V)=∣0⟩⟨0∣⊗U+∣1⟩⟨1∣⊗V
C(U,V) = |0\rangle\langle 0| \otimes U + |1\rangle\langle 1| \otimes V
Step 1: Show that it's unitary
C(U,V)C(U,V)†=∣0⟩⟨0∣⊗UU†+∣1⟩⟨1∣⊗VV†=1
C(U,V) \, C(U,V)^\dagger = |0\rangle\langle 0| \otimes UU^\dagger + |1\rangle\langle 1| \otimes V V^\dagger = \mathbb 1
Key idea for post-Trotter methods
C(U,V)=∣0⟩⟨0∣⊗U+∣1⟩⟨1∣⊗V
C(U,V) = |0\rangle\langle 0| \otimes U + |1\rangle\langle 1| \otimes V
Step 2: Apply to flag qubit in superposition
C(U,V)(∣0⟩+∣1⟩)⊗∣ψ⟩=∣0⟩⊗U∣ψ⟩+∣1⟩⊗V∣ψ⟩
C(U,V) (|0\rangle + |1\rangle) \otimes |\psi\rangle = |0\rangle \otimes U |\psi\rangle + |1\rangle \otimes V |\psi\rangle
Key idea for post-Trotter methods
C(U,V)=∣0⟩⟨0∣⊗U+∣1⟩⟨1∣⊗V
C(U,V) = |0\rangle\langle 0| \otimes U + |1\rangle\langle 1| \otimes V
Step 3: Consider what happens if applied to superposition:
(Rx(θ)⊗1)C(U,V)∣+⟩⊗∣ψ⟩=
(R_x(\theta)\otimes 1)C(U,V) |+\rangle \otimes |\psi\rangle =
Rx(θ)∣0⟩=c∣0⟩+s∣1⟩
R_x(\theta) |0\rangle = c |0\rangle+ s |1\rangle
Rx(θ)∣1⟩=c∣1⟩−s∣0⟩
R_x(\theta) |1\rangle = c |1\rangle -s |0\rangle
∣0⟩⊗(cU−sV)∣ψ⟩+∣1⟩⊗(cV+sU)∣ψ⟩
|0\rangle \otimes (cU -s V) |\psi\rangle + |1\rangle \otimes (cV +sU) |\psi\rangle
Key idea for post-Trotter methods
C(U,V)=∣0⟩⟨0∣⊗U+∣1⟩⟨1∣⊗V
C(U,V) = |0\rangle\langle 0| \otimes U + |1\rangle\langle 1| \otimes V
Step 4: Assume flag is measured with outcome 1 and discard it
(P+⊗1)(Rx(θ)⊗1)C(U,V)∣+⟩⊗∣ψ⟩∝(cU+sV)∣ψ⟩
(P_+\otimes 1)(R_x(\theta)\otimes 1)C(U,V) |+\rangle \otimes |\psi\rangle \propto (cU+s V) |\psi\rangle
Rx(θ)∣0⟩=c∣0⟩+s∣1⟩
R_x(\theta) |0\rangle = c |0\rangle+ s |1\rangle
Rx(θ)∣1⟩=c∣1⟩−s∣0⟩
R_x(\theta) |1\rangle = c |1\rangle -s |0\rangle
Conclusion: We can (probabilistically) apply (normalized) sums of unitary operators
Key idea for reliable post-Trotter methods
R=1−2∣ϕ⟩⟨ϕ∣
R = 1 - 2|\phi\rangle\langle \phi|
Grover reflector
Step 1: Show that it's unitary
...
...
Key idea for reliable post-Trotter methods
R=1−2∣ϕ⟩⟨ϕ∣
R = 1 - 2|\phi\rangle\langle \phi|
Grover reflector
Step 2: Consider applying it to a state overlapping with it
R(∣ϕ⟩+∣ϕ⊥⟩)∝−∣ϕ⟩+∣ϕ⊥⟩
R(|\phi\rangle + |\phi^\perp\rangle) \propto - |\phi\rangle+ |\phi^\perp\rangle
Key idea for reliable post-Trotter methods
R=1−2∣ϕ⟩⟨ϕ∣
R = 1 - 2|\phi\rangle\langle \phi|
Grover reflector
Step 3: Reflect around the linear combination of unitaries
This is also called oblivious amplitude amplification, and the crux is in making this efficiently and obliviously i.e. without knowing or destroying the reflector state
Rc,s=Q(1−∣ϕ⟩⟨ϕ∣)Q†
R_{c,s} = Q(1-|\phi\rangle\langle \phi|)Q^\dagger
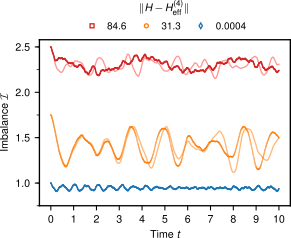
Gaussian quantum simulators
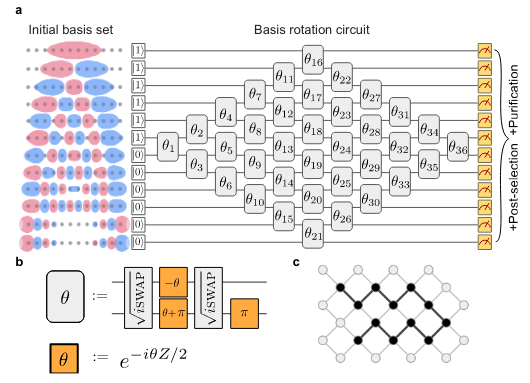
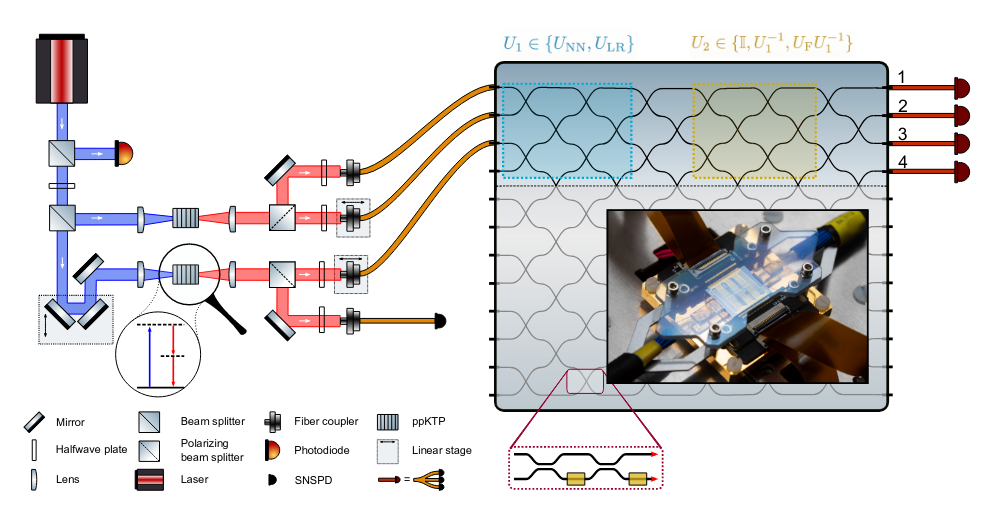
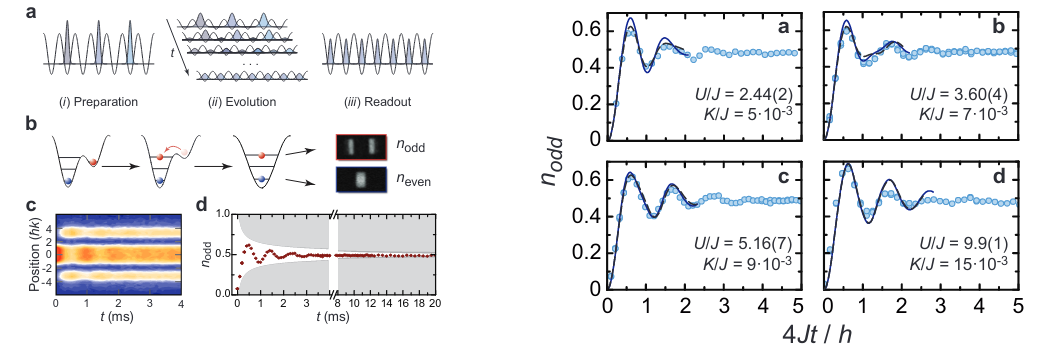
How?
Ultra-cold 1d gases
Inside: atoms
Outside: wavepackets
hydrodynamics
Energy of phonons
E
E
E
E
E
E
E
E
H^TLL=∫dz[2mℏ2nGP∂zφ^2+gδϱ^2]
\hat H_\text{TLL} = \int \text{d}z\left[ \frac{\hbar^2n_{GP}}{2m}\partial_z\hat\varphi^2+g\delta\hat\varrho^2\right]
δϱ
\delta\varrho
∂zφ
\partial_z\varphi
∂zφ
\partial_z\varphi
≪
\ll
δϱ
\delta\varrho
≪
\ll
Tomonaga-Luttinger liquid
Quantum field refrigerators in the TLL model:
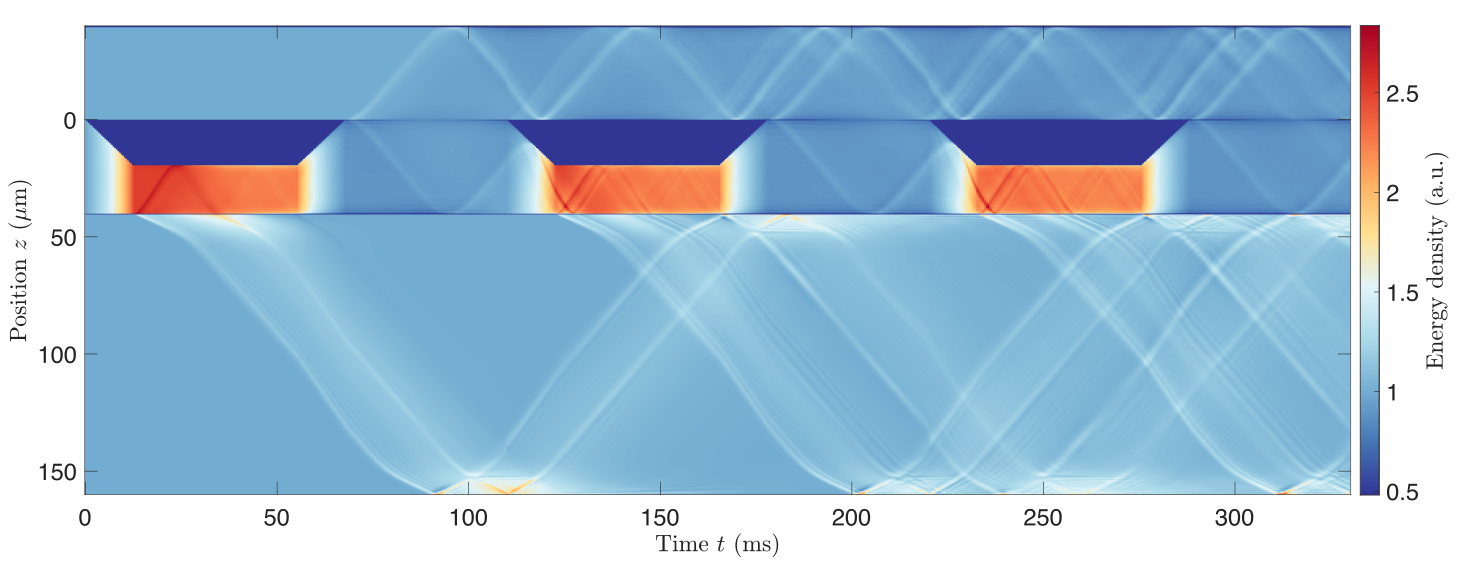
System
Piston
Bath
Bath with excitations
System cooled down
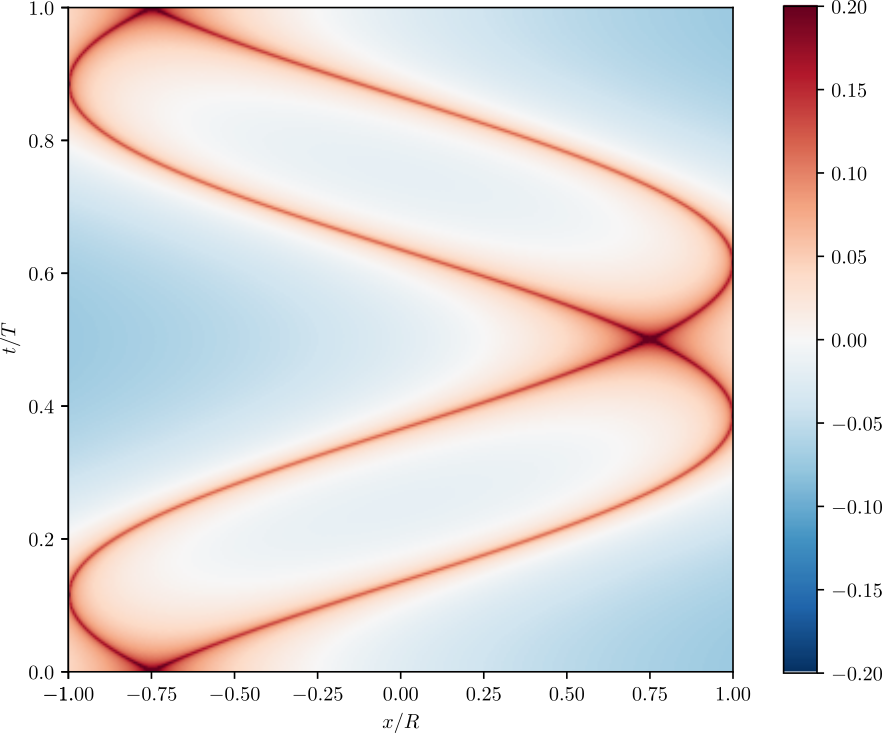
Breaking of the Huygens-Fresnel principle
in the inhomogenous TLL model:
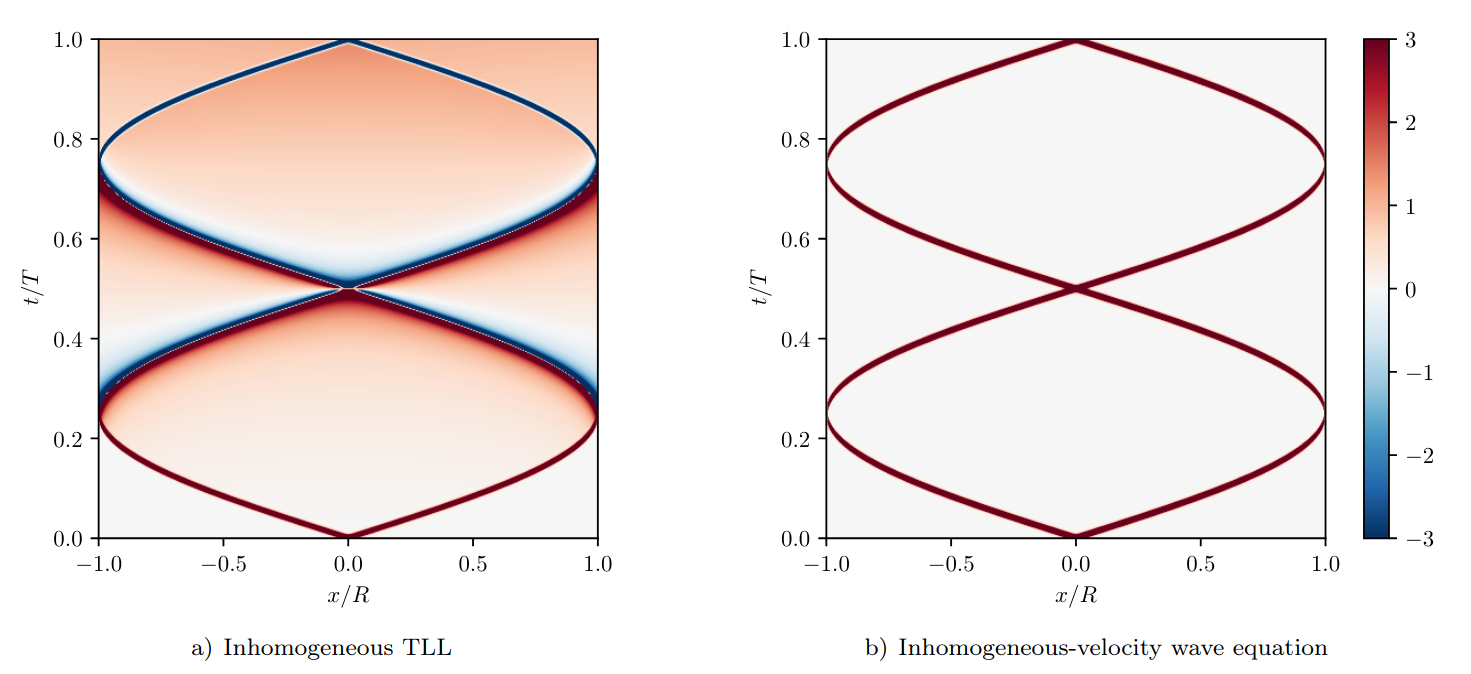
Why?
Why develop continuous field
quantum simulators?
- Representation theory: Quantum information?
- Continuum limits: BQP and QMA or more?
- Are nanowires computationally hard to simulate?
What do we know is difficult?
SM
Fundamental
Universal
Effective
Why develop continuous field
quantum simulators?
- Representation theory: Quantum information?
- Continuum limits: BQP and QMA or more?
- Are nanowires computationally hard to simulate?
What do we know is difficult?
SM
Fundamental
Universal
Effective
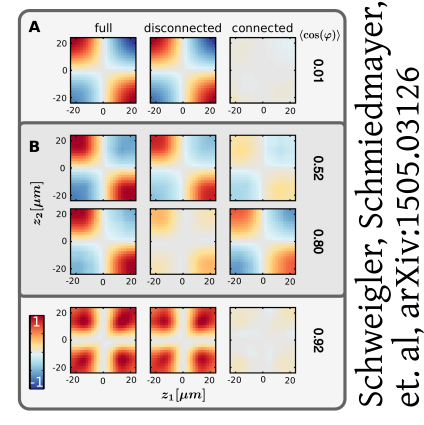
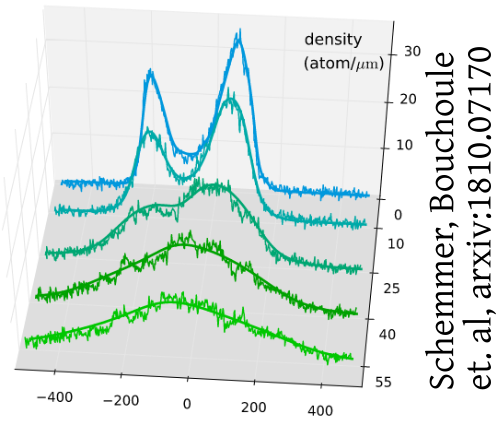
Non-thermal
steady states
Sine-Gordon
thermal states
Atomtronics
Generalized hydrodynamics
Recurrences
Some highlights:
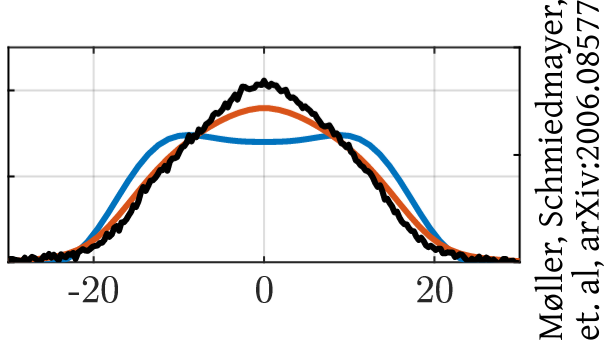
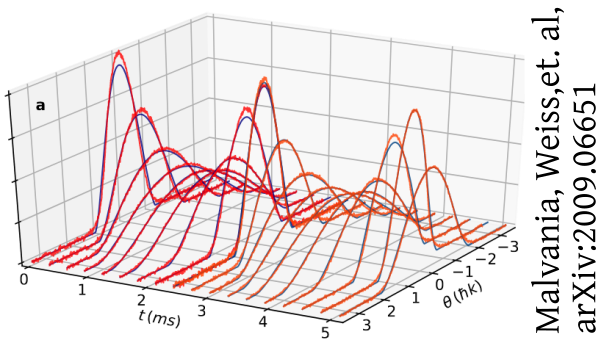
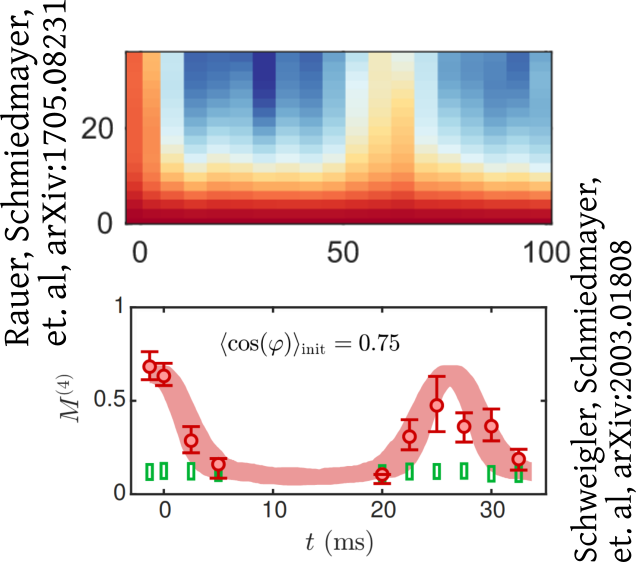
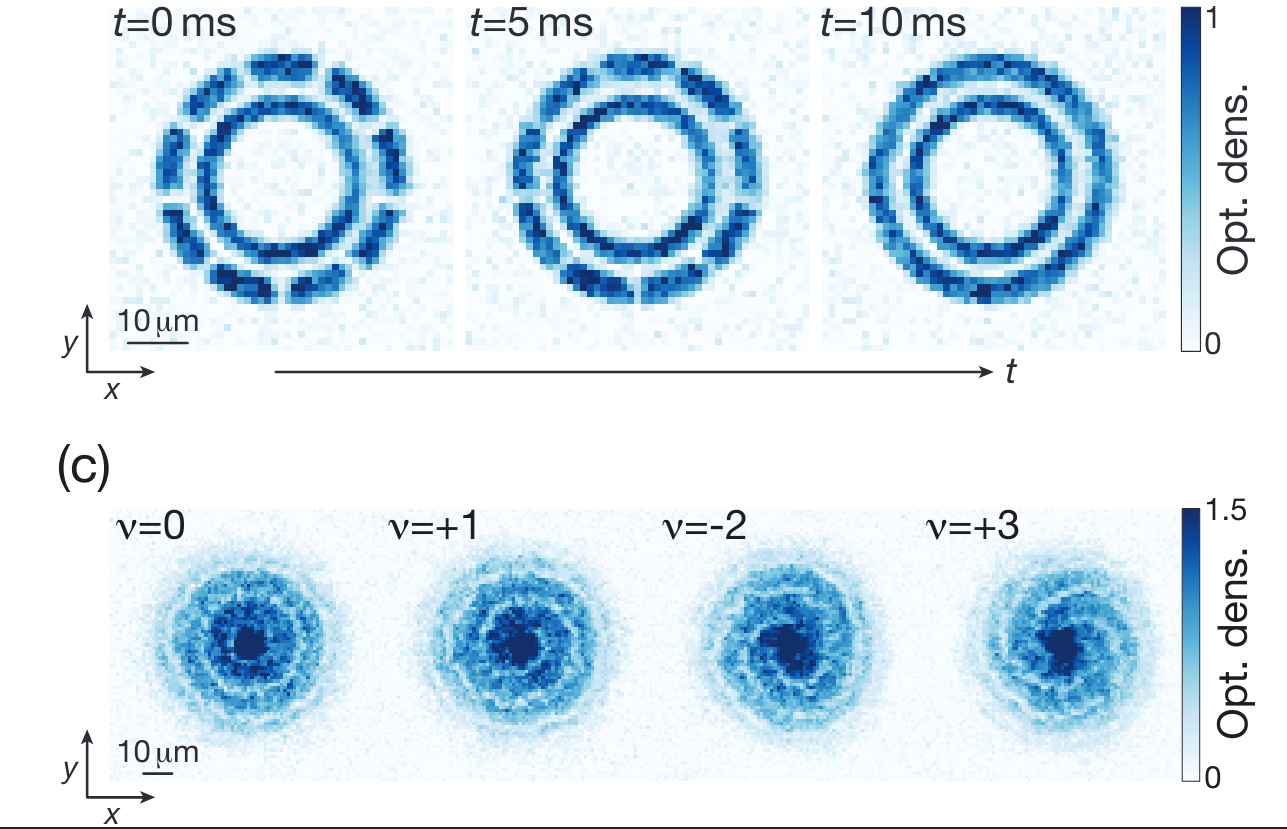
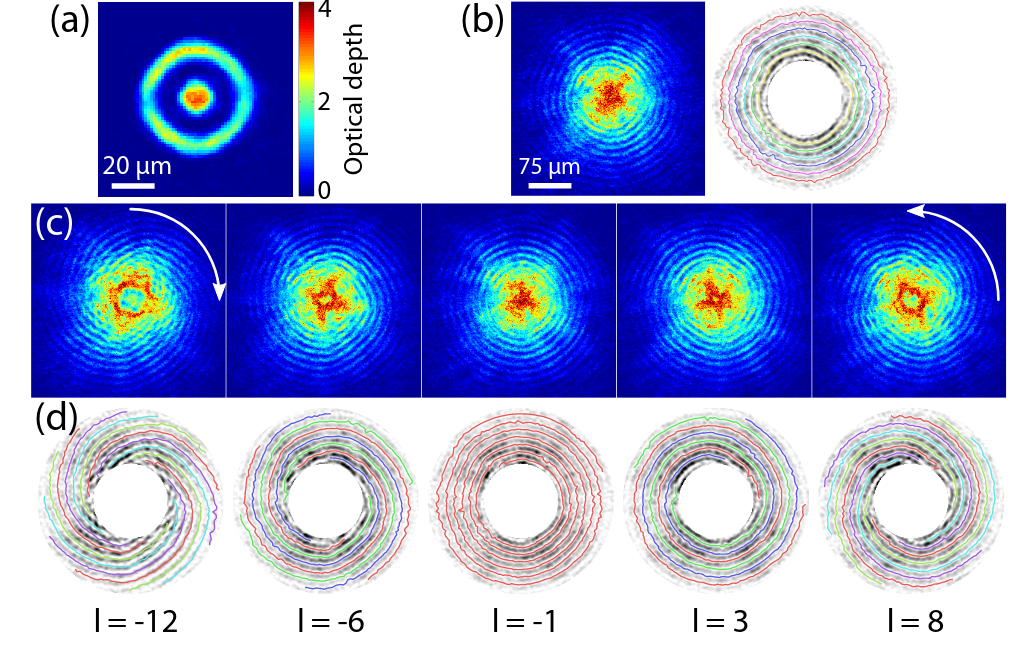
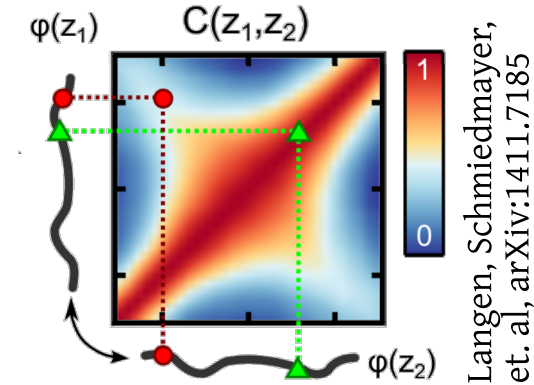
Interferometry measures velocities
van Nieuwkerk, Schmiedmayer, Essler, arXiv:1806.02626
Schumm, Schmiedmayer, Kruger, et al., arXiv:quant-ph/0507047
∂zφ^(z)≈Δzφ^(z)−φ^(z+Δz)
\partial_z\hat \varphi(z) \approx\frac{\hat \varphi(z)-\hat \varphi(z+\Delta z)}{\Delta z}
∂zφ^(z)≈ΔzΔφ^(z)
\partial_z\hat \varphi(z) \approx\frac{\Delta\hat\varphi(z)}{\Delta z}
Δz
\Delta z
Tomography
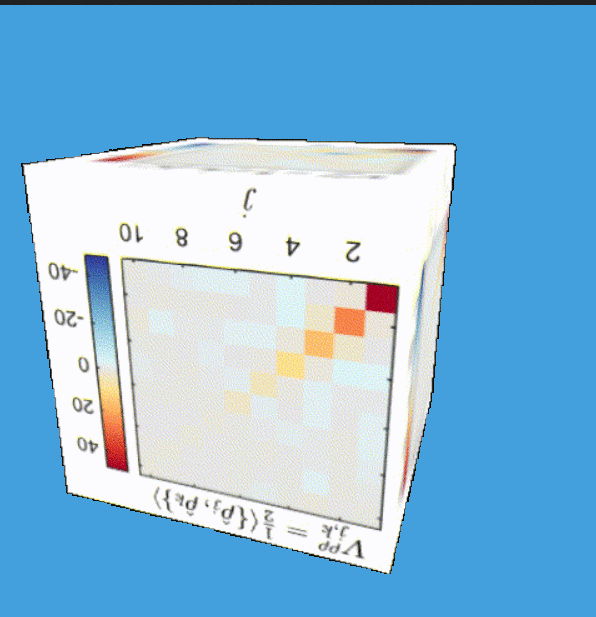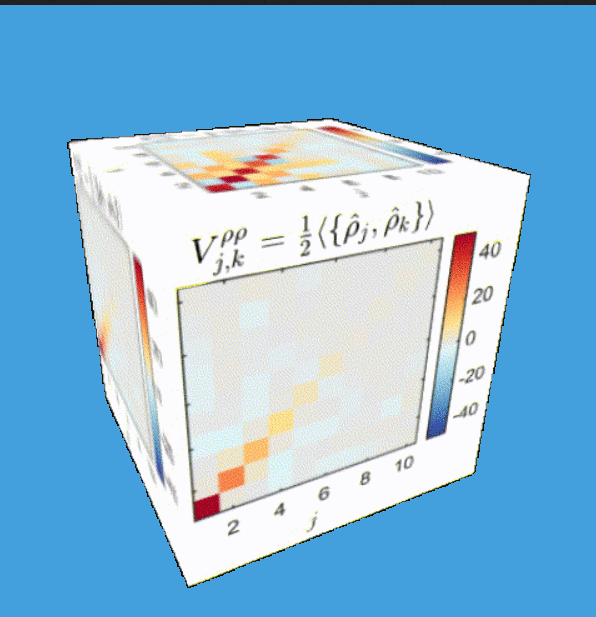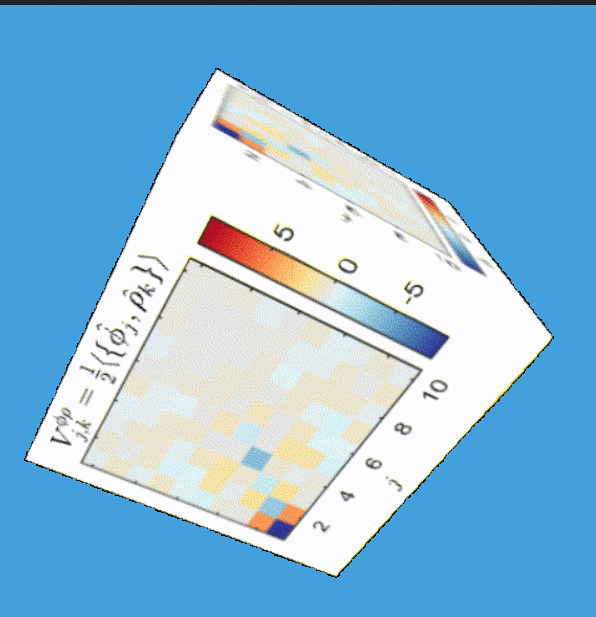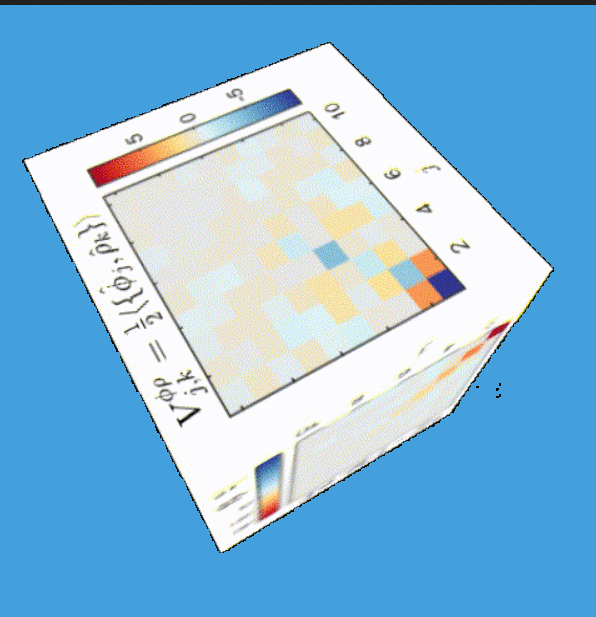
Tomography for phonons
H^TLL=∫dz[2mℏ2nGP∂zφ^2+gδϱ^2]
\hat H_\text{TLL} = \int \text{d}z\left[ \frac{\hbar^2n_{GP}}{2m}\partial_z\hat\varphi^2+g\delta\hat\varrho^2\right]
H^TLL=∑k>02ℏωk(ϕk2+δρ^k2)+gρ^02
\hat H_\text{TLL} = \sum_{k>0} \frac {\hbar \omega_k}2 (\phi_k^2+\delta\hat\rho_k^2) + g\hat\rho_0^2
⟨ϕ^k2(t)⟩=cos2(ωkt)⟨ϕk2(0)⟩+sin2(ωkt)⟨δρ^k2(0)⟩
\langle\hat \phi_k^2(t)\rangle= \cos^2(\omega_k t) \langle \phi_k^2(0)\rangle \\
\quad\quad\quad\quad\quad+\sin^2(\omega_k t) \langle \delta\hat \rho_k^2(0)\rangle
δρ^
\delta \hat\rho
⟨ϕ^2(t)⟩
\langle\hat \phi^2(t)\rangle
⟨δρ^2(0)⟩=0?
\langle\delta\hat \rho^2(0)\rangle =0?
⟨ϕ^2(0)⟩
\langle \hat \phi^2(0)\rangle
ϕ^
\hat \phi
Tomography for phonons
H^TLL=∫dz[2mℏ2nGP∂zφ^2+gδϱ^2]
\hat H_\text{TLL} = \int \text{d}z\left[ \frac{\hbar^2n_{GP}}{2m}\partial_z\hat\varphi^2+g\delta\hat\varrho^2\right]
H^TLL=∑k>02ℏωk(ϕk2+δρ^k2)+gρ^02
\hat H_\text{TLL} = \sum_{k>0} \frac {\hbar \omega_k}2 (\phi_k^2+\delta\hat\rho_k^2) + g\hat\rho_0^2
⟨ϕ^k2(t)⟩=cos2(ωkt)⟨ϕk2(0)⟩+sin2(ωkt)⟨δρ^k2(0)⟩
\langle\hat \phi_k^2(t)\rangle= \cos^2(\omega_k t) \langle \phi_k^2(0)\rangle \\
\quad\quad\quad\quad\quad+\sin^2(\omega_k t) \langle \delta\hat \rho_k^2(0)\rangle
δρ^
\delta \hat\rho
⟨ϕ^2(t)⟩
\langle\hat \phi^2(t)\rangle
⟨δρ^2(0)⟩=0?
\langle\delta\hat \rho^2(0)\rangle =0?
⟨ϕ^2(0)⟩
\langle \hat \phi^2(0)\rangle
ϕ^
\hat \phi
What are eigenmodes?
H^TLL=∫dz[2mℏ2nGP∂zφ^2+gδϱ^2]
\hat H_\text{TLL} = \int \text{d}z\left[ \frac{\hbar^2n_{GP}}{2m}\partial_z\hat\varphi^2+g\delta\hat\varrho^2\right]
H^TLL=∑k>02ℏωk(ϕk2+δρ^k2)+gρ^02
\hat H_\text{TLL} = \sum_{k>0} \frac {\hbar \omega_k}2 (\phi_k^2+\delta\hat\rho_k^2) + g\hat\rho_0^2
ϕ^k=∫0Ldzcos(πkz/L)φ^(z)
\hat \phi_k = \int_0^L dz \cos(\pi k z/L)\hat \varphi(z)
∫0Ldzcos(πkz/L)cos(πk′z/L)=δk,k′
\int_0^L dz \cos(\pi k z/L)\cos(\pi k'z/L) = \delta_{k,k'}
Transmutation
⟨ϕ^k2(t)⟩=cos2(ωkt)⟨ϕ^k2(0)⟩+sin2(ωkt)⟨δρ^k2(0)⟩
\langle\hat \phi_k^2(t)\rangle= \cos^2(\omega_k t) \langle \hat\phi_k^2(0)\rangle +\sin^2(\omega_k t) \langle \delta\hat \rho_k^2(0)\rangle
⟨ϕ^k2(t)⟩=⟨ϕ^k2(0)⟩
\langle\hat \phi_k^2(t)\rangle= \langle \hat\phi_k^2(0)\rangle
⟨ϕ^k2(t)⟩=⟨δρ^k2(0)⟩
\langle\hat \phi_k^2(t)\rangle= \langle \delta\hat \rho_k^2(0)\rangle
t=0:
t=0:
t=2ωkπ:
t=\frac{\pi}{2\omega_k}:
δρ^
\delta \hat\rho
⟨ϕ^2(t)⟩
\langle\hat \phi^2(t)\rangle
⟨δρ^2(0)⟩=0?
\langle\delta\hat \rho^2(0)\rangle =0?
⟨ϕ^2(0)⟩
\langle \hat \phi^2(0)\rangle
ϕ^
\hat \phi
Tomography
A1,2=sin2(ωkt1)
A_{1,2}= \sin^2(\omega_k t_1 )
A1,1=cos2(ωkt1)
A_{1,1}= \cos^2(\omega_k t_1)
⟨ϕ^k2(t)⟩=cos2(ωkt)⟨ϕ^k2(0)⟩+sin2(ωkt)⟨δρ^k2(0)⟩
\langle\hat \phi_k^2(t)\rangle= \cos^2(\omega_k t) \langle \hat\phi_k^2(0)\rangle+ \sin^2(\omega_k t) \langle \delta\hat \rho_k^2(0)\rangle
A3,2=sin2(ωkt3)
A_{3,2}= \sin^2(\omega_k t_3 )
A3,1=cos2(ωkt3)
A_{3,1}= \cos^2(\omega_k t_3)
A2,2=sin2(ωkt2)
A_{2,2}= \sin^2(\omega_k t_2 )
A2,1=cos2(ωkt2)
A_{2,1}= \cos^2(\omega_k t_2)
A(⟨ϕ^k2(0)⟩⟨δρ^k2(0)⟩)=⟨ϕ^k2(t1)⟩⟨ϕ^k2(t2)⟩⟨ϕ^k2(t3)⟩
A
\begin{pmatrix} \langle \hat\phi_k^2(0)\rangle \\\langle \delta\hat \rho_k^2(0)\rangle
\end{pmatrix}
=\begin{pmatrix} \langle \hat\phi_k^2(t_1)\rangle \\\langle \hat\phi_k^2(t_2)\rangle \\\langle \hat\phi_k^2(t_3)\rangle \end{pmatrix}
∥Aq−d∥=min
\|Aq - d\| = \text{min}
(This formalism: Tomography for many modes)
Tomography Klein-Gordon thermal state after quench
H^KG=H^TLL+J∫dznGPφ^2
\hat H_\text{KG}=\hat H_\text{TLL}+J\int \mathrm{d}z \,n_{GP} \hat \varphi^2
Extracting physical properties
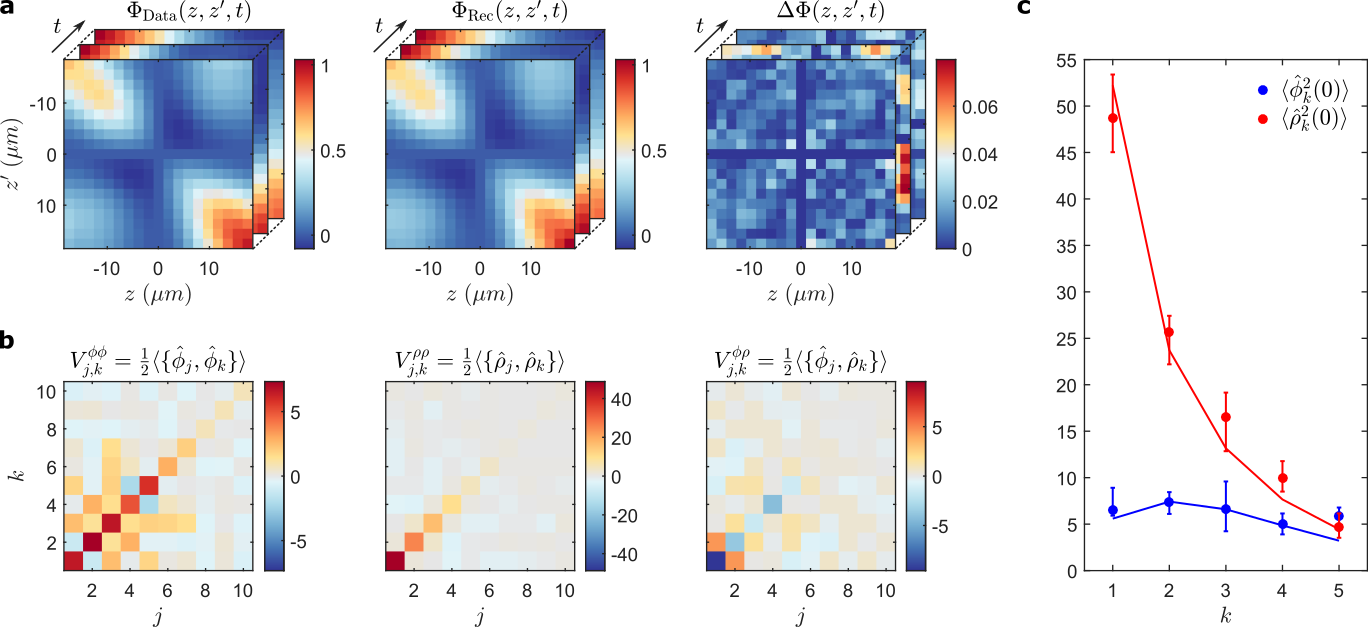
Extracting physical properties
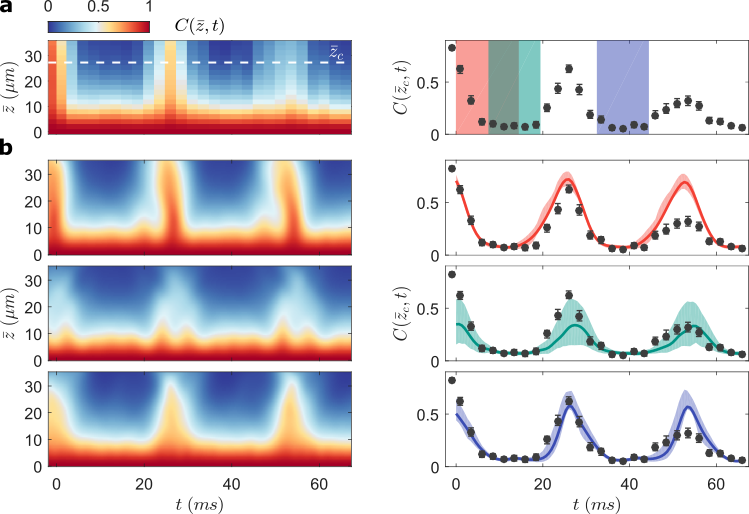
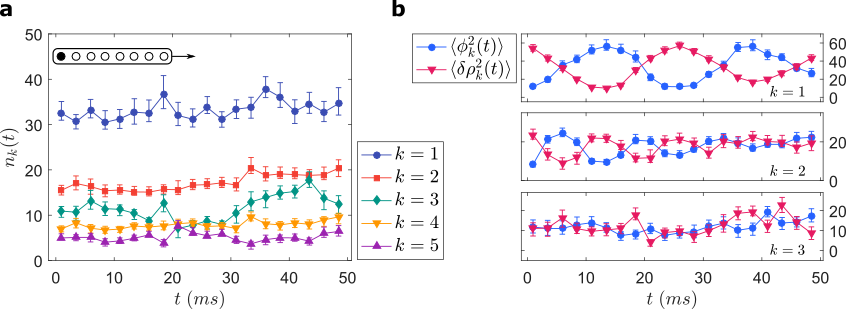
Extracting physical properties
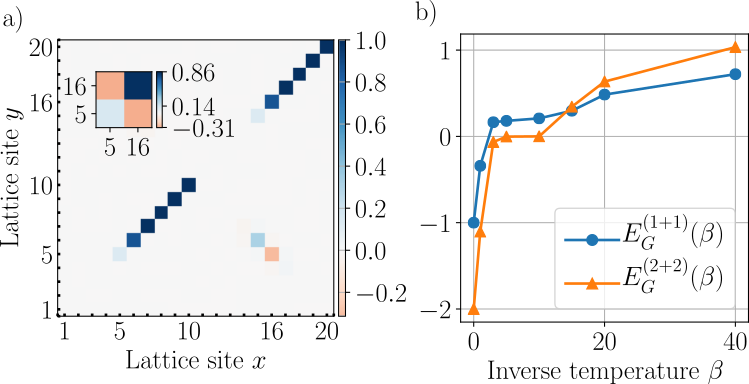
Tomography for optical lattices
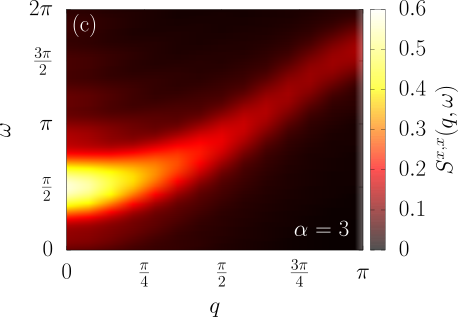
Material science?
0
0
0
0
C
Diagonalization quantum algorithm
DSF of Rydberg arrays
Phonon tomography
Optical lattice tomography
⟨ϕ^k2(t)⟩=cos2(ωkt)⟨ϕk2(0)⟩+sin2(ωkt)⟨δρ^k2(0)⟩
\langle\hat \phi_k^2(t)\rangle= \cos^2(\omega_k t) \langle \phi_k^2(0)\rangle \\
\quad\quad\quad\quad\quad+\sin^2(\omega_k t) \langle \delta\hat \rho_k^2(0)\rangle
δρ^
\delta \hat\rho
⟨ϕ^2(t)⟩
\langle\hat \phi^2(t)\rangle
⟨δρ^2(0)⟩=0?
\langle\delta\hat \rho^2(0)\rangle =0?
⟨ϕ^2(0)⟩
\langle \hat \phi^2(0)\rangle
ϕ^
\hat \phi
Ask me anytime:
0
0
0
0
C
Fidelity witnesses
Tomography optical lattices
Tomography phonons
Proving statistical mechanics
Quantum simulating DSF
Holography in tensor networks
PEPS contraction average #P-hard
Quantum field machine
MBL l-bits
(click links at slides.com/marekgluza
Lecture: Quantum compiling Marek Gluza NTU Singapore slides.com/marekgluza *Background explanation: It's a primitive bricklayer!
Lecture: Quantum compiling
By Marek Gluza
Lecture: Quantum compiling
- 441
