Double-bracket quantum algorithms for diagonalization
Marek Gluza
NTU Singapore
slides.com/marekgluza
Text
Why double a bracket?
∂tA^(t)=i[A^(t),H^(t)]
\partial_t \hat A(t) = i [ \hat A(t), \hat H(t)]
∂tA^(t)=[A^(t),[A^(t),H^(t)]]
\partial_t \hat A(t) = [ \hat A(t), [\hat A(t), \hat H(t)]]
Why double a bracket?
∂tA^(t)=i[H^(t),A^(t)]
\partial_t \hat A(t) = i [ \hat H(t), \hat A(t)]
∂tA^(t)=[H^(t),[H^(t),A^(t)]]
\partial_t \hat A(t) = [ \hat H(t), [\hat H(t), \hat A(t)]]
=
=
2 qubit unitary
Canonical
∂tA^(t)=[A^(t),[A^(t),H^(t)]]
\partial_t \hat A(t) = [ \hat A(t), [\hat A(t), \hat H(t)]]
Double-bracket quantum algorithms
are inspired by double-bracket flows
and allow for quantum compiling of short-depth circuits which approximate grounds states
Inspired by double-bracket flows we compiled quantum circuits which yield quantum states relevant for material science
∂tA^(t)=[A^(t),[A^(t),H^(t)]]
\partial_t \hat A(t) = [ \hat A(t), [\hat A(t), \hat H(t)]]
H^1=es0W^0H^0e−s0W^0
\hat H_1 = e^{s_0 \hat W_0} \hat H_0 e^{-s_0 \hat W_0}
W^0=[D^0,H^0]
\hat W_0
= [\hat D_0,\hat H_0]
Double-bracket rotation ansatz
antihermitian
(iH^)†=−iH^
\left(i\hat H\right)^\dagger = -i \hat H
Rotation generator:
Input:
Unitary rotation:
esW^0
e^{s \hat W_0}
H^0
\hat H_0
Double-bracket rotation:
∂sH^0(s)=[W^0,H^0]
\partial_s \hat H_0(s) = [\hat W_0, \hat H_0]
⇔
\Leftrightarrow
∂sH^0(s)=[H^0(s),[H^0(0),D^0]]
\partial_s \hat H_0(s) = [\hat H_0(s),[ \hat H_0(0),\hat D_0] ]
∂tA^(t)=[A^(t),[A^(t),H^(t)]]
\partial_t \hat A(t) = [ \hat A(t), [\hat A(t), \hat H(t)]]
H^1=es0W^0H^0e−s0W^0
\hat H_1 = e^{s_0 \hat W_0} \hat H_0 e^{-s_0 \hat W_0}
W^0=[D^0,H^0]
\hat W_0
= [\hat D_0,\hat H_0]
Double-bracket rotation ansatz
Rotation generator:
Input:
Unitary rotation:
esW^0
e^{s \hat W_0}
H^0
\hat H_0
Double-bracket rotation:
Key point: If D^0 is diagonal then
H^1 should be "more" diagonal than H^0
H^0(s)=esW^0H^0e−sW^0
\hat H_0(s) = e^{s \hat W_0} \hat H_0 e^{-s \hat W_0}
W^0=[D^0,H^0]
\hat W_0
= [\hat D_0,\hat H_0]
Double-bracket rotation ansatz
Rotation generator:
Input:
H^0
\hat H_0
Double-bracket rotation:
σ(H^0(s))
\sigma(\hat H_0(s))
Restriction to off-diagonal
∂s∥σ(H^0(s))∥HS2=−2⟨W^0,[H^0,σ(H^0)]⟩HS
\partial_s \|\sigma(\hat H_0(s))\|_{\text{HS}}^2 = -2\langle \hat W_0,[\hat H_0, \sigma(\hat H_0)]\rangle_{\text{HS}}
Lemma:
Proof: Taylor expand, shuffle around (fun!)
H^(s)=esW^0H^0e−sW^0
\hat H(s) = e^{s \hat W_0} \hat H_0 e^{-s \hat W_0}
W^0=[D^0,H^0]
\hat W_0
= [\hat D_0,\hat H_0]
Double-bracket rotation ansatz
Rotation generator:
Input:
H^0
\hat H_0
Double-bracket rotation:
σ(H^ℓ)
\sigma(\hat H_\ell)
Restriction to off-diagonal
∂s∥σ(H^0(s))∥HS2=−2⟨W^0,[H^0,σ(H^0)]⟩HS
\partial_s \|\sigma(\hat H_0(s))\|_{\text{HS}}^2 = -2\langle \hat W_0,[\hat H_0, \sigma(\hat H_0)]\rangle_{\text{HS}}
Lemma:
Proof: Taylor expand, shuffle around (fun!)
A new approach to diagonalization on a quantum computer
H^1=esW^1H^e−sW^1
\hat H_1 = e^{s \hat W_1} \hat H e^{-s \hat W_1}
W^k=[Dk−1,H^k−1]
\hat W_k = [D_{k-1},\hat H_{k-1}]
H^k=esW^kH^k−1e−sW^k
\hat H_k = e^{s \hat W_k} \hat H_{k-1} e^{-s \hat W_k}
H^TFIM=∑i=1L−1X^iX^i+1+∑i=1LZ^i
\hat H_\text{TFIM} = \sum_{i=1}^{L-1}\hat X_i\hat X_{i+1}+\sum_{i=1}^L \hat Z_i
Double-bracket iteration
W^1=[D^0,H^0]
\hat W_1 = [\hat D_0,\hat H_0]
∂ℓH^ℓ=[W^ℓ,H^ℓ]
\partial_\ell \hat H_\ell = [\hat W_\ell, \hat H_\ell]
W^ℓ=[Δ(H^ℓ),σ(H^ℓ)]
\hat W_\ell = [\Delta(\hat H_\ell),\sigma(\hat H_\ell)]
Δ(H^ℓ)
\Delta(\hat H_\ell)
σ(H^ℓ)
\sigma(\hat H_\ell)
Głazek-Wilson-Wegner flow
Restriction to off-diagonal
Restriction to diagonal
∂ℓ∥σ(H^ℓ)∥HS2=−2∥W^ℓ∥HS2≤0
\partial_\ell \|\sigma(\hat H_\ell)\|_{\text{HS}}^2 = -2\|\hat W_\ell\|_{\text{HS}}^2 \le 0
as a quantum algorithm
(addendo: where it's coming from)
Unitary U^ℓ such that
\text{Unitary } \hat U_\ell \text{ such that }
W^ℓ=[Δ(H^ℓ),σ(H^ℓ)]
\hat W_\ell = [\Delta(\hat H_\ell),\sigma(\hat H_\ell)]
Głazek-Wilson-Wegner flow
∂ℓ∥σ(H^ℓ)∥HS2=−2∥W^ℓ∥HS2≤0
\partial_\ell \|\sigma(\hat H_\ell)\|_{\text{HS}}^2 = -2\|\hat W_\ell\|_{\text{HS}}^2 \le 0
as a quantum algorithm
H^ℓ=U^ℓH^0U^ℓ†
\hat H_\ell = \hat U_\ell \hat H_0 \hat U_\ell^\dagger
∂ℓH^ℓ=[W^ℓ,H^ℓ]
\partial_\ell \hat H_\ell = [\hat W_\ell, \hat H_\ell]
(addendo: where it's coming from)
New quantum algorithm for diagonalization
\hat H \mapsto \hat \mathcal H_\ell = \hat \mathcal U_\ell^\dagger \hat H \hat\mathcal U_\ell
\partial_\ell \hat \mathcal H_\ell = [[A(\hat \mathcal H_\ell),B(\hat \mathcal H_\ell)], \hat \mathcal H_\ell]
0
0
0
0
D^s(J^)=∏μ∈{0,1}×LZ^μe−isJ^/DZ^μ
\hat D_s(\hat J) = \prod_{\mu\in\{0,1\}^{\times L}} \hat Z_\mu e^{-i s \hat J/D} \hat Z_\mu
C^s(J^)=(D^s/K(J^)†eis/KJ^D^s/K(J^)e−is/KJ^)K
\hat C_s(\hat J) = \left( \hat D_{\sqrt{s/K}}(\hat J)^\dagger \;e^{i\sqrt{s/K}\hat J}\;\hat D_{\sqrt{s/K}}(\hat J)\;e^{-i\sqrt{s/K}\hat J}\right)^K
1) Dephasing
2) Group commutator
3) Frame shifting
\partial_\ell \hat \mathcal H_\ell = [[A(\hat \mathcal H_\ell),B(\hat \mathcal H_\ell)], \hat \mathcal H_\ell]
V^k=C^s(J^1)C^s(J^2)…C^s(J^k−1)≈e−sW^1e−sW^2…e−sW^k−1
\hat V_k = \hat C_s(\hat J_{1})\; \hat C_s(\hat J_{2})\ldots \hat C_s(\hat J_{k-1}) \approx e^{-s \hat W_1}\;e^{-s \hat W_2}\ldots e^{-s \hat W_{k-1}}
Fun but painful because probably not possible efficiently
What about other methods?
0
0
0
0
Universal gate set:
single qubit rotations + generic 2 qubit gate
Universal gate set can approximate any unitary
What is a universal quantum computer?
∣ψ⟩=U∣00…0⟩
|\psi\rangle = U |00\ldots0\rangle
quantum compiling approximates unitaries with circuits
⇒U≈Uc
\Rightarrow U \approx U_c
Quantum compiling
2x2 unitary matrix - use Euler angles
4x4 unitary matrix - use KAK decomposition + 3x CNOT formula
CNOT=∣0⟩⟨0∣⊗(1001)+∣1⟩⟨1∣⊗(0110)
\text{CNOT} = |0\rangle\langle 0|\otimes \begin{pmatrix} 1 & 0\\ 0 &1\end{pmatrix}
+ |1\rangle\langle1 |\otimes \begin{pmatrix} 0 & 1\\ 1 &0\end{pmatrix}
=
=
2 qubit unitary
Canonical
KAK decomposition, Brockett's work etc
=
2 qubit unitaries modulo single qubit unitaries are a 3 dimensional torus
Quantum compiling
2 qubits - 4×4 unitary matrix - use KAK decomposition + 3 CNOT formula
Quantum compiling
1 qubit - 2×2 unitary matrix - use Euler angles
n qubits - 2n unitary matrix - use quantum Shannon decomposition + O(4n) CNOT formula
Variational quantum eigensolver
0
0
0
0
+
+
+
+
+
This works but is inefficient
This is efficient but doesn't work
Open: fill this gap!
W^k=[D^k−1,H^k−1]
\hat W_k = [\hat D_{k-1},\hat H_{k-1}]
H^k=eskW^kH^k−1e−skW^k
\hat H_k = e^{s_k \hat W_k} \hat H_{k-1} e^{-s_k \hat W_k}
Double-bracket iteration
sk
s_k
Rotation durations:
Input:
H^0
\hat H_0
D^k
\hat D_k
Diagonal generators:
A new approach to diagonalization on a quantum computer
Great: we can diagonalize
How to quantum compile?
How to quantum?
Group commutator
\hat H \mapsto \hat \mathcal H_\ell = \hat \mathcal U_\ell^\dagger \hat H \hat\mathcal U_\ell
0
0
0
0
Want
H^k+1=esW^kH^ke−sW^k
\hat H_{k+1} = e^{s \hat W_k} \hat H_k e^{-s \hat W_k}
W^k=[D^k,H^k]
\hat W_k = [\hat D_k, \hat H_k]
eiskD^keiskH^ke−iskD^ke−iskH^k=e−s[D^k,H^k]+E^(GC)
e^{i\sqrt{s_k}\hat D_k}e^{i\sqrt{s_k}\hat H_k}e^{-i\sqrt{s_k}\hat D_k}e^{-i\sqrt{s_k}\hat H_k}= e^{-s[\hat D_k,\hat H_k]} +\hat E^\text{(GC)}
New bound
∥E^(GC)∥≤4∥H^0∥∥[D^k,H^k]∥s3
\|\hat E^\text{(GC)}\| \le 4\|\hat H_0\|\,\|[\hat D_k, \hat H_k]\| s^3
Group commutator during iteration
0
0
0
0
H^k=U^k†H^0U^k
\hat H_{k} = \hat U_k^\dagger \hat H_0 \hat U_k
V^0=eis0D^0eis0H^0e−is0D^0e−is0H^0
\hat V_0 = e^{i\sqrt{s_0}\hat D_0}e^{i\sqrt{s_0}\hat H_0}e^{-i\sqrt{s_0}\hat D_0}e^{-i\sqrt{s_0}\hat H_0}
e−itH^k=e−itU^k†H^0U^k=U^k†e−tH^0U^k
e^{-it \hat H_{k} } = e^{-it \hat U_k^\dagger \hat H_0 \hat U_k}= \hat U_k^\dagger e^{-t \hat H_0} \hat U_k
V^1=eis1D^1eis1H^1e−is1D^1e−is1H^1
\hat V_1 = e^{i\sqrt{s_1}\hat D_1}e^{i\sqrt{s_1}\hat H_{1}} e^{-i\sqrt{s_1}\hat D_1}e^{-i\sqrt{s_1}\hat H_{1}}
U^k=V^0V^1…V^k
\hat U_k =\hat V_0 \hat V_1 \ldots \hat V_k
Group commutator during iteration
0
0
0
0
H^k=U^k†H^0U^k
\hat H_{k} = \hat U_k^\dagger \hat H_0 \hat U_k
V^0=eis0D^0eis0H^0e−is0D^0e−is0H^0
\hat V_0 = e^{i\sqrt{s_0}\hat D_0}e^{i\sqrt{s_0}\hat H_0}e^{-i\sqrt{s_0}\hat D_0}e^{-i\sqrt{s_0}\hat H_0}
e−itH^k=e−itU^k†H^0U^k=U^k†e−tH^0U^k
e^{-it \hat H_{k} } = e^{-it \hat U_k^\dagger \hat H_0 \hat U_k}= \hat U_k^\dagger e^{-t \hat H_0} \hat U_k
V^1=eis1D^1V^0†eis1H^0V^0e−is1D^1V^0†e−is1H^0V^0
\hat V_1 = e^{i\sqrt{s_1}\hat D_1}\hat V_{0}^\dagger e^{i\sqrt{s_1}\hat H_{0}}\hat V_0 e^{-i\sqrt{s_1}\hat D_1}\hat V_{0}^\dagger e^{-i\sqrt{s_1}\hat H_{0}}\hat V_0
U^k=V^0V^1…V^k
\hat U_k =\hat V_0 \hat V_1 \ldots \hat V_k
V^k=eiskD^kU^k−1†eiskH^0U^k−1e−iskD^kU^k−1†e−iskH^0U^k−1
\hat V_k = e^{i\sqrt{s_k}\hat D_k}\hat U_{k-1}^\dagger e^{i\sqrt{s_k}\hat H_{0}}\hat U_{k-1} e^{-i\sqrt{s_k}\hat D_k}\hat U_{k-1}^\dagger
e^{-i\sqrt{s_k}\hat H_{0}}\hat U_{k-1}
W^k=[D^k−1,H^k−1]
\hat W_k = [\hat D_{k-1},\hat H_{k-1}]
H^k=eskW^kH^k−1e−skW^k
\hat H_k = e^{s_k \hat W_k} \hat H_{k-1} e^{-s_k \hat W_k}
Double-bracket iteration
sk
s_k
Rotation durations:
Input:
H^0
\hat H_0
D^k
\hat D_k
Diagonal generators:
A new approach to diagonalization on a quantum computer
Great: we can diagonalize
How to quantum compile?
Replace by the group commutator
e−s[D^k,H^k]≈eisD^keisH^ke−isD^ke−isH^k
e^{-s[\hat D_k,\hat H_k]}\approx e^{i\sqrt{s}\hat D_k}e^{i\sqrt{s}\hat H_k}e^{-i\sqrt{s}\hat D_k}e^{-i\sqrt{s}\hat H_k}
Group commutator iteration
V^k=eiskD^keiskH^ke−iskD^ke−iskH^k
\hat V_k = e^{i\sqrt{s_k}\hat D_k}e^{i\sqrt{s_k}\hat H_k}e^{-i\sqrt{s_k}\hat D_k}e^{-i\sqrt{s_k}\hat H_k}
H^k+1=V^k†H^kV^k
\hat H_{k+1} = \hat V_{k}^\dagger\hat H_{k} \hat V_k
V^k=e−s[D^k,H^k]
\hat V_{k} = e^{-s[\hat D_{k},\hat H_{k}]}
Double-bracket iteration
Double-bracket iteration
Transition from theory to QPUs
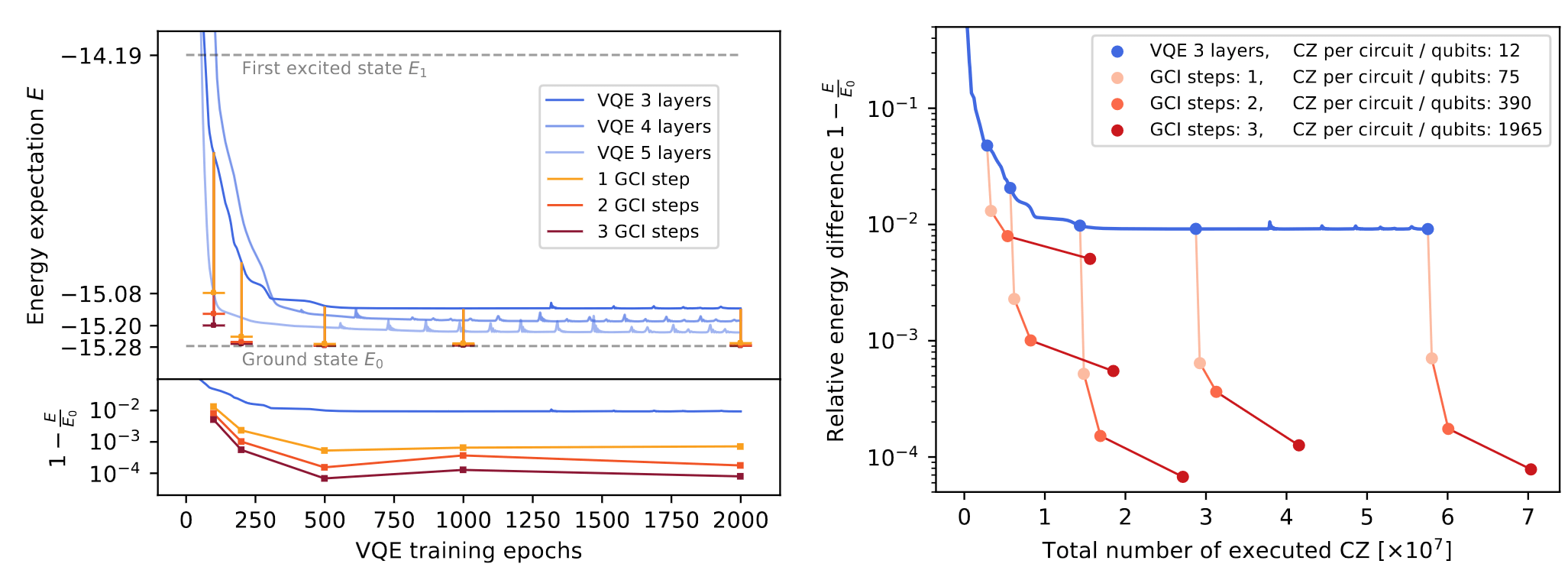
How well does it work?
Variational flow example
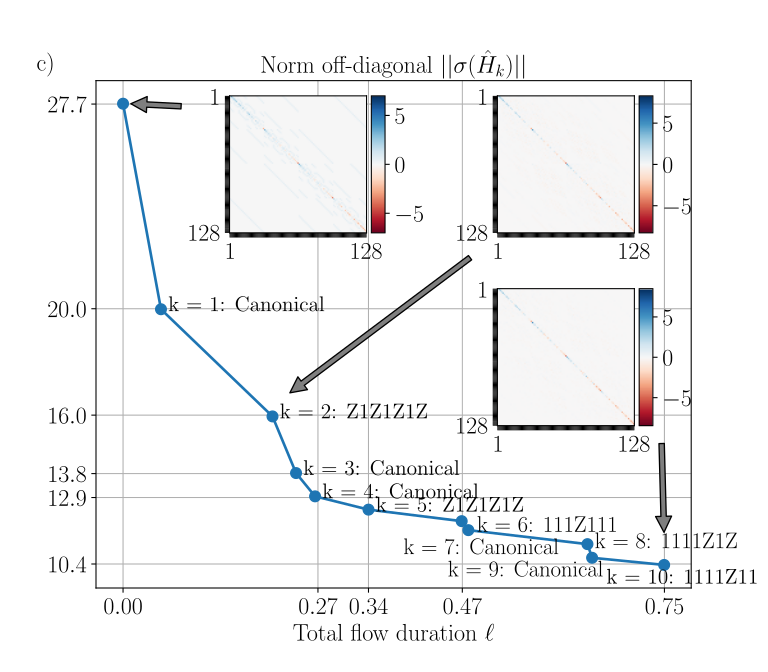
Notice the steady increase of diagonal dominance.
Variational vs. GWW flow
Notice that degeneracies limit GWW diagonalization but variational brackets can lift them.
GWW for 9 qubits
Notice the spectrum is almost converged.
GWW for 9 qubits
Notice that some of them are essentially eigenstates!
How does it work after warm-start?
10 qubit, 50 layers of CNOT - 99.5% ground state fidelity
A^0=j=1∑L(XjXj+1+YjYj+1+ZjZj+1)
\hat A_0 = \sum_{j=1}^L(X_j X_{j+1}+Y_j Y_{j+1}+ Z_j Z_{j+1})
This both works and is efficient
How to interface VQE and DBQA?
Quantum Dynamic Programming
with J. Son, R. Takagi and N. Ng
QDP code structure
Warm-start unitary from variational quantum eigensolver
0
0
0
0
+
+
+
+
+
=
=
=Uθ
= U_\theta
DBQA input with warmstart
A^0→H^0=U^θ†A^0U^θ
\hat A_0 \rightarrow \hat H_0 = \hat U_\theta^\dagger \hat A_0 \hat U_\theta
V0=eis0D^0eis0H^0e−is0D^0e−is0H^0
V_0 = e^{i\sqrt{s_0}\hat D_0}e^{i\sqrt{s_0}\hat H_0}e^{-i\sqrt{s_0}\hat D_0}e^{-i\sqrt{s_0}\hat H_0}
V0=eis0D^0U^θ†eis0A^0U^θe−is0D^0U^θ†e−is0A^0U^θ
V_0 = e^{i\sqrt{s_0}\hat D_0}\hat U_\theta^\dagger e^{i\sqrt{s_0}\hat A_0}\hat U_\theta
e^{-i\sqrt{s_0}\hat D_0}\hat U_\theta^\dagger e^{-i\sqrt{s_0}\hat A_0}\hat U_\theta
Use unitarity and get circuit VQE insertions
10 qubit, 50 layers of CNOT - 99.5% ground state fidelity
A^0=j=1∑L(XjXj+1+YjYj+1+ZjZj+1)≡j=1∑LA^0(j)
\hat A_0 = \sum_{j=1}^L(X_j X_{j+1}+Y_j Y_{j+1}+ Z_j Z_{j+1}) \equiv \sum_{j=1}^L\hat A_0^{(j)}
e−itA^0≈(j=1∏Le−itA^0(j)/M)M
e^{-it\hat A_0} \approx \left( \prod_{j=1}^L e^{-i t\hat A_0^{(j)}/M}\right)^M
e−itA^0(j)/M=
e^{-i t\hat A_0^{(j)}/M}=
=
=
2 qubit unitary
Canonical
Canonical
For quantum compiling we use:
- higher-order group commutators
- higher-order Trotter-Suzuki decomposition
- 3-CNOT formulas
New quantum algorithm for diagonalization
\hat H \mapsto \hat \mathcal H_\ell = \hat \mathcal U_\ell^\dagger \hat H \hat\mathcal U_\ell
\partial_\ell \hat \mathcal H_\ell = [[A(\hat \mathcal H_\ell),B(\hat \mathcal H_\ell)], \hat \mathcal H_\ell]
no qubit overheads
no controlled-unitaries
0
0
0
0
C
0
0
0
0
Simple
=
Easy
Doesn't spark joy :(
Double-bracket quantum algorithm for diagonalization
H^↦H^ℓ=U^ℓ†H^U^ℓ
\hat H \mapsto \hat H_\ell = \hat U_\ell^\dagger \hat H \hat U_\ell
∂ℓH^ℓ=[[A(H^ℓ),B(H^ℓ)],H^ℓ]
\partial_\ell \hat H_\ell = [[A(\hat H_\ell),B(\hat H_\ell)], \hat H_\ell]
new approach to preparing useful states
0
0
0
0
What else is there?
Linear programming
Matching optimization
Diagonalization
Sorting
QR decomposition
Toda flow
∂ℓH^ℓ=[[A(H^ℓ),B(H^ℓ)],H^ℓ]
\partial_\ell \hat H_\ell = [[A(\hat H_\ell), B(\hat H_\ell)] , \hat H_\ell]
Double-bracket flow
Runtime-boosting heuristics
Analytical convergence analysis
Group commutator bound
Hasting's conjecture
Relation to other quantum algorithms
Code is available on Github
0
0
0
0
C
Double-bracket quantum algorithms for diagonalization
with J. Son, R. Takagi and N. Ng
EQDP(N,ρ,M):=(E1/M(N,ρ))M
\mathcal{E}^{(\mathcal{N},\rho,M)}_{QDP} \coloneqq (\mathcal{E}^{(\mathcal{N},\rho)}_{1/M})^M
Quantum dynamic programming
Material science?
0
0
0
0
C
Double-bracket quantum algorithms for diagonalization Marek Gluza NTU Singapore slides.com/marekgluza https://arxiv.org/abs/2206.11772 Text
Copy of Version 2024: Double-bracket quantum algorithms for diagonalization
By Marek Gluza
Copy of Version 2024: Double-bracket quantum algorithms for diagonalization
- 179
