Double-bracket quantum algorithms
Marek Gluza
NTU Singapore
Scan QR code or go to slides.com/marekgluza
How do you create a quantum algorithm?
- Now: Not many distinct quantum algorithms
https://quantumalgorithmzoo.org/ - Why?
- 90's Shor: factoring is in BQP
- 00's Shor: Why have not more algorithms have been found? https://cs.brynmawr.edu/Courses/cs380/fall2012/Shor2003.pdf
Either because the easy ones are efficient classically or we have no good language
- Classically: Reduction to decision problems
- Quantumly: Is \(\langle\psi|H|\psi\rangle\) lower than ...?
- Optimization: Only quadratic speed-up?
- Grand unification of quantum algorithms https://arxiv.org/abs/2105.02859 through block-encodings
- Another unification through double-bracket flows and Riemannian optimization - this talk
- Double-bracket quantum algorithms give intuition why unification possible: \(\langle\psi|H|\psi\rangle\) is optimization so interpret through Riemannian gradients
Click links at slides.com/marekgluza
4 stages of creating quantum algorithms
1. Design choice:
How to go about it?
|\psi(\tau)\rangle = \frac{e^{-\tau H}|\psi\rangle}{\| e^{-\tau H}|\psi\rangle\|}
2. Unitary synthesis:
How to do it?
3. Circuit compilation:
What gates to do?
0. Problem choice:
What challenge to take up?
Double-bracket quantum algorithms:
Systematic framework for unitary synthesis
Design choices for optimization
| Diagonalization |
|
Inefficient? |
|---|---|---|
|
Imaginary-time evolution |
Non-unitary? | |
| Quantum signal processing | Probabilistic? |
U^\dagger H U =
\begin{pmatrix}
\lambda_0&&\\
&\lambda_1&\\
&&\ddots
\end{pmatrix}
|\psi(\tau)\rangle = \frac{e^{-\tau H}|\psi\rangle}{\| e^{-\tau H}|\psi\rangle\|}
|\psi(z)\rangle = \frac{ \prod_{k=1}^K(H-z_k I)|\psi\rangle}{\| \prod_{k=1}^K(H-z_k I)|\psi\rangle\|}
Double-bracket quantum algorithms
Click these links at slides.com/marekgluza
| Diagonalization | https://arxiv.org/abs/2206.11772 | ||
|---|---|---|---|
| Imaginary-time evolution | https://arxiv.org/abs/2412.04554 | ||
| Quantum signal processing | https://arxiv.org/abs/2504.01077 | ||
| Grover's search | https://arxiv.org/abs/2507.15065 | Approximates ITE |
U^\dagger H U =
\begin{pmatrix}
\lambda_0&&\\
&\lambda_1&\\
&&\ddots
\end{pmatrix}
|\psi(\tau)\rangle = \frac{e^{-\tau H}|\psi\rangle}{\| e^{-\tau H}|\psi\rangle\|}
\frac{ \prod_{k=1}^K(H-z_k I)|\psi\rangle}{\| \prod_{k=1}^K(H-z_k I)|\psi\rangle\|}
\prod_{k=1}^Ke^{i\theta_k|\psi_k\rangle\langle\psi_k|} e^{s_k[|\psi_k\rangle\langle\psi_k|,H]}|\psi\rangle
H' = e^{-s[D,H]}H e^{s[D,H]}
e^{s[|\psi\rangle\langle\psi|,H]}|\psi\rangle +O(\tau^2)
(1-2|\psi\rangle\langle\psi|)\times e^{i t H_f}
e^{s[|\psi\rangle\langle\psi|,H]}|\psi\rangle
Riemannian gradient: Unique vector \(g\) such that the directional derivative is a projection onto \(g\)
\nabla_A f(x) = \frac{ f(x+s A) - f(x)}{s} = \langle g, A\rangle
\nabla_A f(x) = \frac{ \langle \psi| e^{-isA}He^{isA}- H | \psi\rangle}{s} = \langle \psi| i [H,A] |\psi\rangle
Tr(ABC) = Tr(CAB)\\
\Downarrow \\
Tr(|\psi\rangle\langle \psi| [H,A] ) = Tr([|\psi\rangle\langle \psi|,H]A)
Riemannian gradient: Unique vector \(g\) such that the directional derivative is a projection onto \(g\)
\nabla_A f(x) = \langle g, A\rangle
\nabla_A E(\psi) =
\langle [|\psi\rangle\langle \psi|,H] , i A\rangle_{\rm{HS}}
\\\Downarrow\\
g \equiv [|\psi\rangle\langle \psi|,H]
|\psi'\rangle = e^{s[|\psi\rangle\langle \psi|,H]} |\psi\rangle
|\psi\rangle
|\psi''\rangle = e^{s[|\psi'\rangle\langle \psi'|,H]} |\psi'\rangle
Double-bracket quantum algorithms:
Systematic framework for implementing exponentials of commutators and uncovering new unitary synthesis formulas
Double-bracket quantum algorithms
Click these links at slides.com/marekgluza
| Diagonalization | https://arxiv.org/abs/2206.11772 | ||
|---|---|---|---|
| Imaginary-time evolution | https://arxiv.org/abs/2412.04554 | ||
| Quantum signal processing | https://arxiv.org/abs/2504.01077 | ||
| Grover's search | https://arxiv.org/abs/2507.15065 | Approximates ITE |
U^\dagger H U =
\begin{pmatrix}
\lambda_0&&\\
&\lambda_1&\\
&&\ddots
\end{pmatrix}
|\psi(\tau)\rangle = \frac{e^{-\tau H}|\psi\rangle}{\| e^{-\tau H}|\psi\rangle\|}
\frac{ \prod_{k=1}^K(H-z_k I)|\psi\rangle}{\| \prod_{k=1}^K(H-z_k I)|\psi\rangle\|}
\prod_{k=1}^Ke^{i\theta_k|\psi_k\rangle\langle\psi_k|} e^{s_k[|\psi_k\rangle\langle\psi_k|,H]}|\psi\rangle
H' = e^{-s[D,H]}H e^{s[D,H]}
e^{s[|\psi\rangle\langle\psi|,H]}|\psi\rangle +O(\tau^2)
(1-2|\psi\rangle\langle\psi|)\times e^{i t H_f}
e^{s[|\psi\rangle\langle\psi|,H]}|\psi\rangle
Double-bracket flows
\partial_t O(t)= i[H,O(t)]
\partial_t \rho(t)= i[H,\rho(t)]
\partial_t A(t)= [[A(t),B],A(t)]
H \sim -i[A(t),B]
|
Heisenberg picture |
Linear, variable: observable |
|---|---|
|
Schroedinger picture |
Linear, variable: density matrix |
|
Double-bracket flow |
Non-linear, variable: density matrix or observable The solution is a unitary rotation because |
Double-bracket quantum algorithms
Click these links at slides.com/marekgluza
| Diagonalization |
|
arxiv:2206.11772 |
|---|---|---|
|
Imaginary-time evolution |
https://arxiv.org/abs/2412.04554 | |
|
Quantum signal processing |
https://arxiv.org/abs/2504.01077 |
U^\dagger H U =
\begin{pmatrix}
\lambda_0&&\\
&\lambda_1&\\
&&\ddots
\end{pmatrix}
|\psi(\tau)\rangle = \frac{e^{-\tau H}|\psi\rangle}{\| e^{-\tau H}|\psi\rangle\|}
Brockett flow
\partial_\ell H(\ell)= [[H(\ell),D],H(\ell)]
Głazek-Wilson-Wegner flow
\partial_t H(\ell)= [[H(\ell),\Delta(H(\ell)],H(\ell)]
\partial_\tau \psi(\tau) = [[\psi(\tau) ,H],\psi(\tau) ]
|\psi(p)\rangle= \prod_{k=1}^Ke^{i\theta_k|\psi_k\rangle\langle\psi_k|} e^{s_k[|\psi_k\rangle\langle\psi_k|,H]}|\psi\rangle
|\psi(\tau)\rangle = \frac{e^{-\tau H}|\psi\rangle}{\| e^{-\tau H}|\psi\rangle\|}
|\psi(p)\rangle = \frac{ p(H)|\psi\rangle}{\| p(H)|\psi\rangle\|}
|\psi(p)\rangle = \frac{ p(H)|\psi\rangle}{\| p(H)|\psi\rangle\|}
3 stages of creating quantum algorithms
1. Design choice:
How to go about it?
|\psi(\tau)\rangle = \frac{e^{-\tau H}|\psi\rangle}{\| e^{-\tau H}|\psi\rangle\|}
3. Circuit compilation:
What gates to do?
|\psi(\tau)\rangle = \frac{e^{-\tau H}|\psi\rangle}{\| e^{-\tau H}|\psi\rangle\|}
0. Problem choice:
What challenge to take up?
2. Unitary synthesis:
How to do it?
Double-bracket quantum algorithms:
Systematic framework for unitary synthesis
|\psi(\tau)\rangle = \frac{e^{-\tau H}|\psi\rangle}{\| e^{-\tau H}|\psi\rangle\|}
= e^{\tau[|\psi\rangle\langle\psi|,H]}|\psi\rangle +O(\tau^2)
|\psi(\tau)\rangle = \frac{e^{-\tau H}|\psi\rangle}{\| e^{-\tau H}|\psi\rangle\|} \\
= e^{\tau[|\psi\rangle\langle\psi|,H]}|\psi\rangle +O(\tau^2)\\
= e^{i\sqrt{\tau}H}e^{i\sqrt{\tau}|\psi\rangle\langle\psi|}e^{i\sqrt{\tau}H}|\psi\rangle + O(\tau^{3/2})
e^{itH}\\
e^{it|\psi\rangle\langle\psi|}
Product formula approximation:
\(e^{\tau[|\psi\rangle\langle\psi|,H]}| = e^{i\sqrt{\tau}H}e^{i\sqrt{\tau}|\psi\rangle\langle\psi|}e^{-i\sqrt{\tau}H}e^{-i\sqrt{\tau}|\psi\rangle\langle\psi|} + O(\tau^{3/2})\)
Product formula approximation:
\(e^{\tau[|\psi\rangle\langle\psi|,H]}| = e^{i\sqrt{\tau}H}e^{i\sqrt{\tau}|\psi\rangle\langle\psi|}e^{-i\sqrt{\tau}H}e^{-i\sqrt{\tau}|\psi\rangle\langle\psi|} + O(\tau^{3/2})\)
Quantum algorithm DB-QITE - iterate recursively:
- Define \(|{\psi_k}\rangle = U_k |0\rangle\)
- Use \(e^{it |\psi_k\rangle\langle\psi_k|} = U_ke^{it |0\rangle\langle0|}U_k^\dagger \)
- Recursively iterate \( U_{k+1} = e^{is H} U_k e^{is |0\rangle\langle 0|} U_k^\dagger e^{-is H} U_k\)
3 stages of creating quantum algorithms
1. Design choice:
How to go about it?
|\psi(\tau)\rangle = \frac{e^{-\tau H}|\psi\rangle}{\| e^{-\tau H}|\psi\rangle\|}
3. Circuit compilation:
What gates to do?
|\psi(\tau)\rangle = \frac{e^{-\tau H}|\psi\rangle}{\| e^{-\tau H}|\psi\rangle\|}
0. Problem choice:
What challenge to take up?
2. Unitary synthesis:
How to do it?
e^{itH}\\
e^{it|\psi\rangle\langle\psi|}
Two theorems for DB-QITE:
DB-QITE:
- Define \(|{\psi_k}\rangle = U_k |0\rangle\)
- Recursively iterate \( U_{k+1} = e^{is H} U_k e^{is |0\rangle\langle 0|} U_k^\dagger e^{-is H} U_k\)
Then:
1. Mean energy \(E_k := \langle \psi_k| H|{\psi_k}\rangle\) decreases as
\(E_{k+1} = E_k - 2s V_k + O(s^2)\)
where \(V_k := \langle \psi_k| H^2|{\psi_k}\rangle - E_k^2\)
2. Ground-state fidelity \(F_k := \langle \lambda| {\psi_k}\rangle\) increases as
\(F_{k} \ge 1 - q^k\)
where \(q = 1 - O( \Delta F_0 / \|H\|^3\)
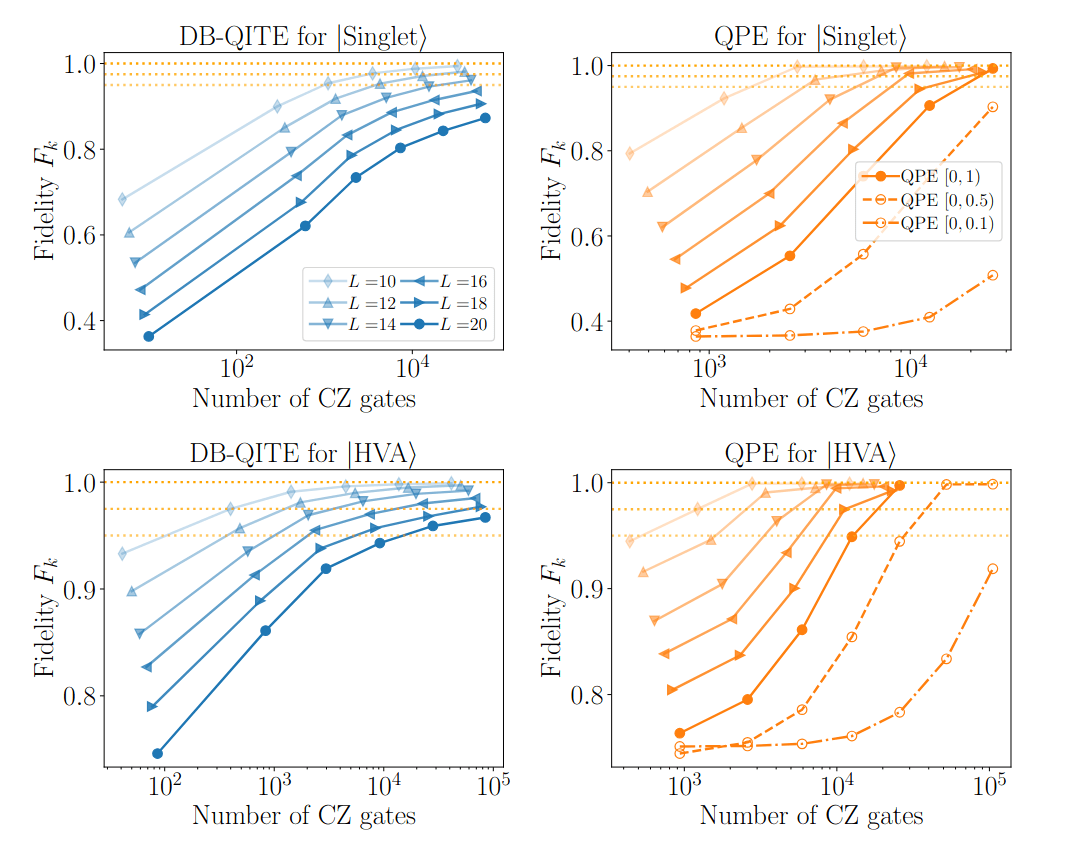
Numerical results for DB-QITE:
DB-QITE:
- Define \(|{\psi_k}\rangle = U_k |0\rangle\)
- Recursively iterate \( U_{k+1} = e^{is H} U_k e^{is |0\rangle\langle 0|} U_k^\dagger e^{-is H} U_k\)
Then:
Double-bracket quantum algorithms
- coherently implement Riemannian gradient steps
-
give rigorous unitary synthesis for
- imaginary-time evolution
- quantum signal processing
- diagonalization unitaries
- Grover's algorithm is an approximation to imaginary-time evolution
J. Son
B. Tiang
S. Carrazza
R. Seidel
R. Zander
Z. Holmes
Y. Suzuki
Tell me when not fast enough? Get stuck? Something else?
Your input is needed to improve them!
N. Ng
Double-bracket quantum algorithms
Click these links at slides.com/marekgluza
| Diagonalization | https://arxiv.org/abs/2206.11772 | ||
|---|---|---|---|
| Imaginary-time evolution | https://arxiv.org/abs/2412.04554 | ||
| Quantum signal processing | https://arxiv.org/abs/2504.01077 | ||
| Grover's search | https://arxiv.org/abs/2507.15065 | Approximates ITE |
U^\dagger H U =
\begin{pmatrix}
\lambda_0&&\\
&\lambda_1&\\
&&\ddots
\end{pmatrix}
|\psi(\tau)\rangle = \frac{e^{-\tau H}|\psi\rangle}{\| e^{-\tau H}|\psi\rangle\|}
\frac{ \prod_{k=1}^K(H-z_k I)|\psi\rangle}{\| \prod_{k=1}^K(H-z_k I)|\psi\rangle\|}
\prod_{k=1}^Ke^{i\theta_k|\psi_k\rangle\langle\psi_k|} e^{s_k[|\psi_k\rangle\langle\psi_k|,H]}|\psi\rangle
H' = e^{-s[D,H]}H e^{s[D,H]}
e^{s[|\psi\rangle\langle\psi|,H]}|\psi\rangle +O(\tau^2)
(1-2|\psi\rangle\langle\psi|)\times e^{i t H_f}
e^{s[|\psi\rangle\langle\psi|,H]}|\psi\rangle
Why double a bracket?
\partial_t \hat A(t) = i [ \hat A(t), \hat H(t)]
\partial_t \hat A(t) = [ \hat A(t), [\hat A(t), \hat H(t)]]
Why double a bracket?
\partial_t \hat A(t) = i [ \hat H(t), \hat A(t)]
\partial_t \hat A(t) = [ \hat H(t), [\hat H(t), \hat A(t)]]
=
2 qubit unitary
Canonical
\partial_t \hat A(t) = [ \hat A(t), [\hat A(t), \hat H(t)]]
Double-bracket quantum algorithms
are inspired by double-bracket flows
and allow for quantum compiling of short-depth circuits which approximate grounds states
Inspired by double-bracket flows we compiled quantum circuits which yield quantum states relevant for material science
\partial_t \hat A(t) = [ \hat A(t), [\hat A(t), \hat H(t)]]
=
2 qubit unitary
Canonical
\hat H_1 = e^{s_0 \hat W_0} \hat H_0 e^{-s_0 \hat W_0}
\hat W_0
= [\hat D_0,\hat H_0]
Double-bracket rotation ansatz
antihermitian
\left(i\hat H\right)^\dagger = -i \hat H
Rotation generator:
Input:
Unitary rotation:
e^{s \hat W_0}
\hat H_0
Double-bracket rotation:
\partial_s \hat H_0(s) = [\hat W_0, \hat H_0]
\Leftrightarrow
\partial_s \hat H_0(s) = [\hat H_0(s),[ \hat H_0(0),\hat D_0] ]
\partial_t \hat A(t) = [ \hat A(t), [\hat A(t), \hat H(t)]]
\hat H_1 = e^{s_0 \hat W_0} \hat H_0 e^{-s_0 \hat W_0}
\hat W_0
= [\hat D_0,\hat H_0]
Double-bracket rotation ansatz
Rotation generator:
Input:
Unitary rotation:
e^{s \hat W_0}
\hat H_0
Double-bracket rotation:
Key point: If \(\hat D_0\) is diagonal then
\(\hat H_1\) should be "more" diagonal than \(\hat H_0\)
\hat H_0(s) = e^{s \hat W_0} \hat H_0 e^{-s \hat W_0}
\hat W_0
= [\hat D_0,\hat H_0]
Double-bracket rotation ansatz
Rotation generator:
Input:
\hat H_0
Double-bracket rotation:
\sigma(\hat H_0(s))
Restriction to off-diagonal
\partial_s \|\sigma(\hat H_0(s))\|_{\text{HS}}^2 = -2\langle \hat W_0,[\hat H_0, \sigma(\hat H_0)]\rangle_{\text{HS}}
Lemma:
Proof: Taylor expand, shuffle around (fun!)
\hat H(s) = e^{s \hat W_0} \hat H_0 e^{-s \hat W_0}
\hat W_0
= [\hat D_0,\hat H_0]
Double-bracket rotation ansatz
Rotation generator:
Input:
\hat H_0
Double-bracket rotation:
\sigma(\hat H_\ell)
Restriction to off-diagonal
\partial_s \|\sigma(\hat H_0(s))\|_{\text{HS}}^2 = -2\langle \hat W_0,[\hat H_0, \sigma(\hat H_0)]\rangle_{\text{HS}}
Lemma:
Proof: Taylor expand, shuffle around (fun!)
A new approach to diagonalization on a quantum computer
\hat H_1 = e^{s \hat W_1} \hat H e^{-s \hat W_1}
\hat W_k = [D_{k-1},\hat H_{k-1}]
\hat H_k = e^{s \hat W_k} \hat H_{k-1} e^{-s \hat W_k}
\hat H_\text{TFIM} = \sum_{i=1}^{L-1}\hat X_i\hat X_{i+1}+\sum_{i=1}^L \hat Z_i
Double-bracket iteration
\hat W_1 = [\hat D_0,\hat H_0]
\partial_\ell \hat H_\ell = [\hat W_\ell, \hat H_\ell]
\hat W_\ell = [\Delta(\hat H_\ell),\sigma(\hat H_\ell)]
\Delta(\hat H_\ell)
\sigma(\hat H_\ell)
Głazek-Wilson-Wegner flow
Restriction to off-diagonal
Restriction to diagonal
\partial_\ell \|\sigma(\hat H_\ell)\|_{\text{HS}}^2 = -2\|\hat W_\ell\|_{\text{HS}}^2 \le 0
as a quantum algorithm
(addendo: where it's coming from)
\text{Unitary } \hat U_\ell \text{ such that }
\hat W_\ell = [\Delta(\hat H_\ell),\sigma(\hat H_\ell)]
Głazek-Wilson-Wegner flow
\partial_\ell \|\sigma(\hat H_\ell)\|_{\text{HS}}^2 = -2\|\hat W_\ell\|_{\text{HS}}^2 \le 0
as a quantum algorithm
\hat H_\ell = \hat U_\ell \hat H_0 \hat U_\ell^\dagger
\partial_\ell \hat H_\ell = [\hat W_\ell, \hat H_\ell]
(addendo: where it's coming from)
New quantum algorithm for diagonalization
\hat H \mapsto \hat \mathcal H_\ell = \hat \mathcal U_\ell^\dagger \hat H \hat\mathcal U_\ell
\partial_\ell \hat \mathcal H_\ell = [[A(\hat \mathcal H_\ell),B(\hat \mathcal H_\ell)], \hat \mathcal H_\ell]
0
0
0
0
\hat D_s(\hat J) = \prod_{\mu\in\{0,1\}^{\times L}} \hat Z_\mu e^{-i s \hat J/D} \hat Z_\mu
\hat C_s(\hat J) = \left( \hat D_{\sqrt{s/K}}(\hat J)^\dagger \;e^{i\sqrt{s/K}\hat J}\;\hat D_{\sqrt{s/K}}(\hat J)\;e^{-i\sqrt{s/K}\hat J}\right)^K
1) Dephasing
2) Group commutator
3) Frame shifting
\partial_\ell \hat \mathcal H_\ell = [[A(\hat \mathcal H_\ell),B(\hat \mathcal H_\ell)], \hat \mathcal H_\ell]
\hat V_k = \hat C_s(\hat J_{1})\; \hat C_s(\hat J_{2})\ldots \hat C_s(\hat J_{k-1}) \approx e^{-s \hat W_1}\;e^{-s \hat W_2}\ldots e^{-s \hat W_{k-1}}
Fun but painful because probably not possible efficiently
What about other methods?
0
0
0
0
Universal gate set:
single qubit rotations + generic 2 qubit gate
Universal gate set can approximate any unitary
What is a universal quantum computer?
|\psi\rangle = U |00\ldots0\rangle
quantum compiling approximates unitaries with circuits
\Rightarrow U \approx U_c
Quantum compiling
2x2 unitary matrix - use Euler angles
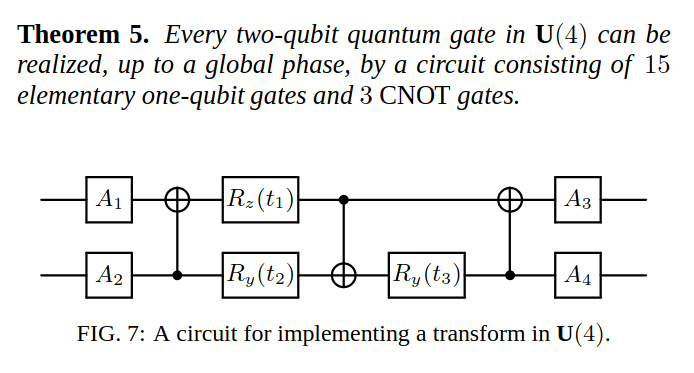
4x4 unitary matrix - use KAK decomposition + 3x CNOT formula
\text{CNOT} = |0\rangle\langle 0|\otimes \begin{pmatrix} 1 & 0\\ 0 &1\end{pmatrix}
+ |1\rangle\langle1 |\otimes \begin{pmatrix} 0 & 1\\ 1 &0\end{pmatrix}
=
2 qubit unitary
Canonical
KAK decomposition, Brockett's work etc
=
2 qubit unitaries modulo single qubit unitaries are a 3 dimensional torus
Quantum compiling
\(2\) qubits - \(4\times 4\) unitary matrix - use KAK decomposition + \(3\) CNOT formula
Quantum compiling
\(1\) qubit - \(2\times 2\) unitary matrix - use Euler angles
\(n\) qubits - \(2^n\) unitary matrix - use quantum Shannon decomposition + \(O(4^n)\) CNOT formula
Variational quantum eigensolver
0
0
0
0
+
+
+
+
+
This works but is inefficient
This is efficient but doesn't work
Open: fill this gap!
\hat W_k = [\hat D_{k-1},\hat H_{k-1}]
\hat H_k = e^{s_k \hat W_k} \hat H_{k-1} e^{-s_k \hat W_k}
Double-bracket iteration
s_k
Rotation durations:
Input:
\hat H_0
\hat D_k
Diagonal generators:
A new approach to diagonalization on a quantum computer
Great: we can diagonalize
How to quantum compile?
How to quantum?
Group commutator
\hat H \mapsto \hat \mathcal H_\ell = \hat \mathcal U_\ell^\dagger \hat H \hat\mathcal U_\ell
0
0
0
0
Want
\hat H_{k+1} = e^{s \hat W_k} \hat H_k e^{-s \hat W_k}
\hat W_k = [\hat D_k, \hat H_k]
e^{i\sqrt{s_k}\hat D_k}e^{i\sqrt{s_k}\hat H_k}e^{-i\sqrt{s_k}\hat D_k}e^{-i\sqrt{s_k}\hat H_k}= e^{-s[\hat D_k,\hat H_k]} +\hat E^\text{(GC)}
New bound
\|\hat E^\text{(GC)}\| \le 4\|\hat H_0\|\,\|[\hat D_k, \hat H_k]\| s^3
Group commutator during iteration
0
0
0
0
\hat H_{k} = \hat U_k^\dagger \hat H_0 \hat U_k
\hat V_0 = e^{i\sqrt{s_0}\hat D_0}e^{i\sqrt{s_0}\hat H_0}e^{-i\sqrt{s_0}\hat D_0}e^{-i\sqrt{s_0}\hat H_0}
e^{-it \hat H_{k} } = e^{-it \hat U_k^\dagger \hat H_0 \hat U_k}= \hat U_k^\dagger e^{-t \hat H_0} \hat U_k
\hat V_1 = e^{i\sqrt{s_1}\hat D_1}e^{i\sqrt{s_1}\hat H_{1}} e^{-i\sqrt{s_1}\hat D_1}e^{-i\sqrt{s_1}\hat H_{1}}
\hat U_k =\hat V_0 \hat V_1 \ldots \hat V_k
Group commutator during iteration
0
0
0
0
\hat H_{k} = \hat U_k^\dagger \hat H_0 \hat U_k
\hat V_0 = e^{i\sqrt{s_0}\hat D_0}e^{i\sqrt{s_0}\hat H_0}e^{-i\sqrt{s_0}\hat D_0}e^{-i\sqrt{s_0}\hat H_0}
e^{-it \hat H_{k} } = e^{-it \hat U_k^\dagger \hat H_0 \hat U_k}= \hat U_k^\dagger e^{-t \hat H_0} \hat U_k
\hat V_1 = e^{i\sqrt{s_1}\hat D_1}\hat V_{0}^\dagger e^{i\sqrt{s_1}\hat H_{0}}\hat V_0 e^{-i\sqrt{s_1}\hat D_1}\hat V_{0}^\dagger e^{-i\sqrt{s_1}\hat H_{0}}\hat V_0
\hat U_k =\hat V_0 \hat V_1 \ldots \hat V_k
\hat V_k = e^{i\sqrt{s_k}\hat D_k}\hat U_{k-1}^\dagger e^{i\sqrt{s_k}\hat H_{0}}\hat U_{k-1} e^{-i\sqrt{s_k}\hat D_k}\hat U_{k-1}^\dagger
e^{-i\sqrt{s_k}\hat H_{0}}\hat U_{k-1}
\hat W_k = [\hat D_{k-1},\hat H_{k-1}]
\hat H_k = e^{s_k \hat W_k} \hat H_{k-1} e^{-s_k \hat W_k}
Double-bracket iteration
s_k
Rotation durations:
Input:
\hat H_0
\hat D_k
Diagonal generators:
A new approach to diagonalization on a quantum computer
Great: we can diagonalize
How to quantum compile?
Replace by the group commutator
e^{-s[\hat D_k,\hat H_k]}\approx e^{i\sqrt{s}\hat D_k}e^{i\sqrt{s}\hat H_k}e^{-i\sqrt{s}\hat D_k}e^{-i\sqrt{s}\hat H_k}
Group commutator iteration
\hat V_k = e^{i\sqrt{s_k}\hat D_k}e^{i\sqrt{s_k}\hat H_k}e^{-i\sqrt{s_k}\hat D_k}e^{-i\sqrt{s_k}\hat H_k}
\hat H_{k+1} = \hat V_{k}^\dagger\hat H_{k} \hat V_k
\hat V_{k} = e^{-s[\hat D_{k},\hat H_{k}]}
Double-bracket iteration
Double-bracket iteration
Transition from theory to QPUs
How well does it work?
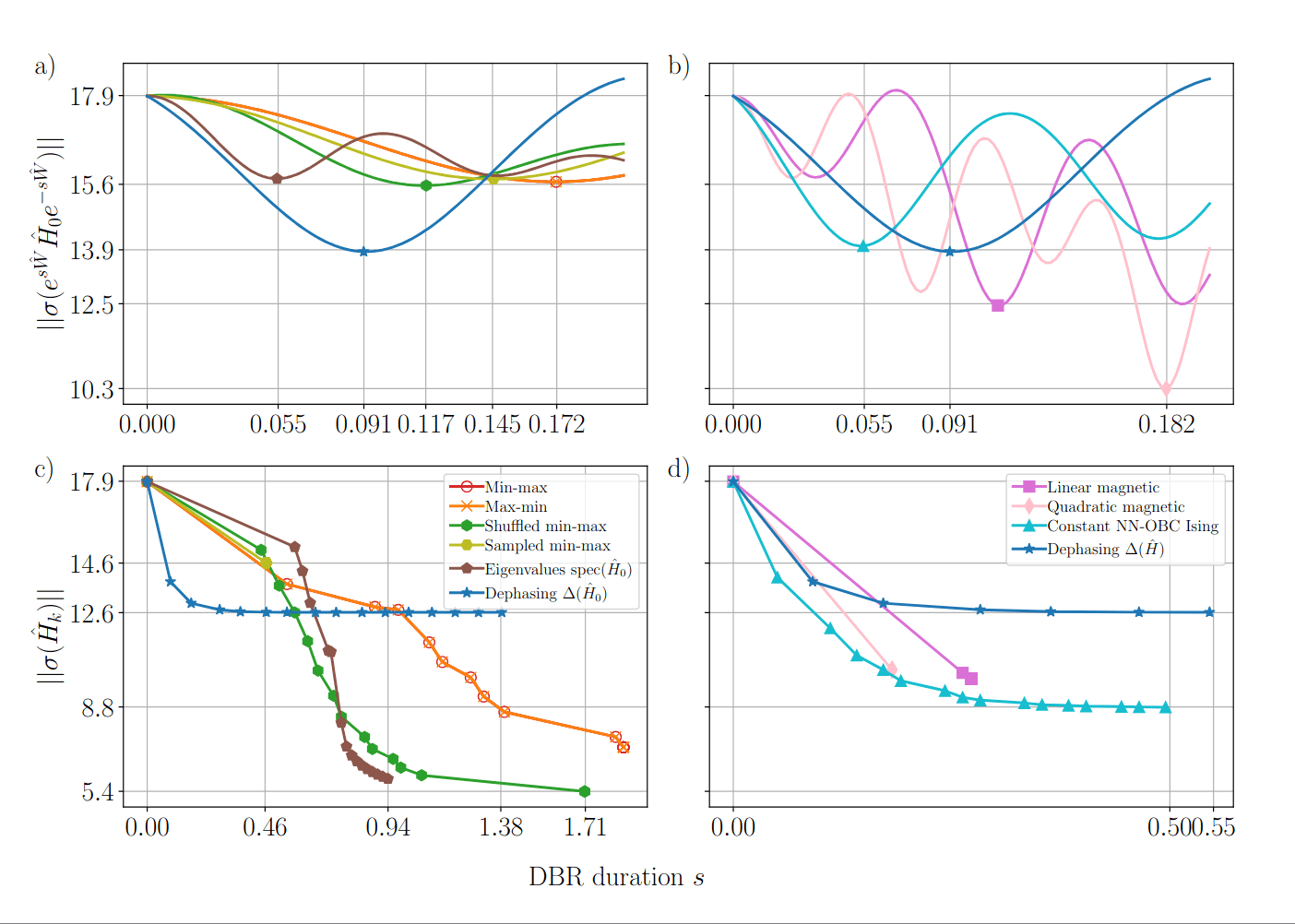
Variational flow example
Notice the steady increase of diagonal dominance.
Variational vs. GWW flow
Notice that degeneracies limit GWW diagonalization but variational brackets can lift them.
GWW for 9 qubits
Notice the spectrum is almost converged.
GWW for 9 qubits
Notice that some of them are essentially eigenstates!
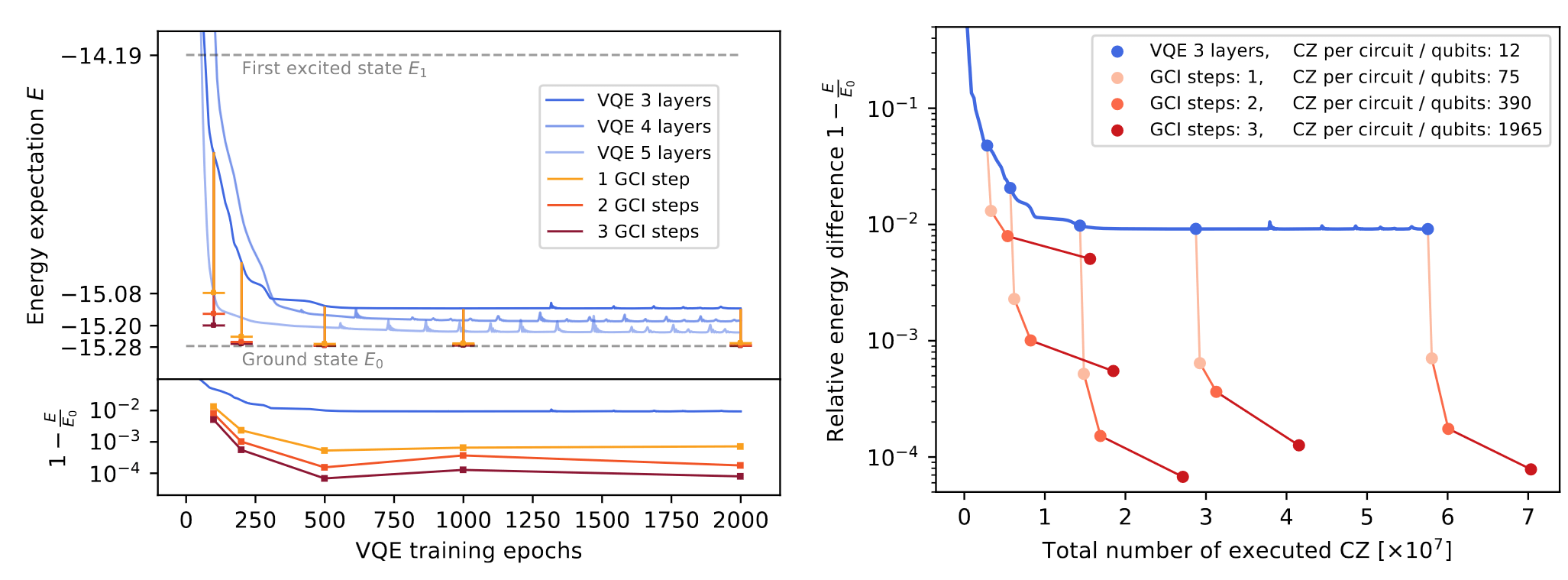
How does it work after warm-start?
10 qubit, 50 layers of CNOT - 99.5% ground state fidelity
\hat A_0 = \sum_{j=1}^L(X_j X_{j+1}+Y_j Y_{j+1}+ Z_j Z_{j+1})
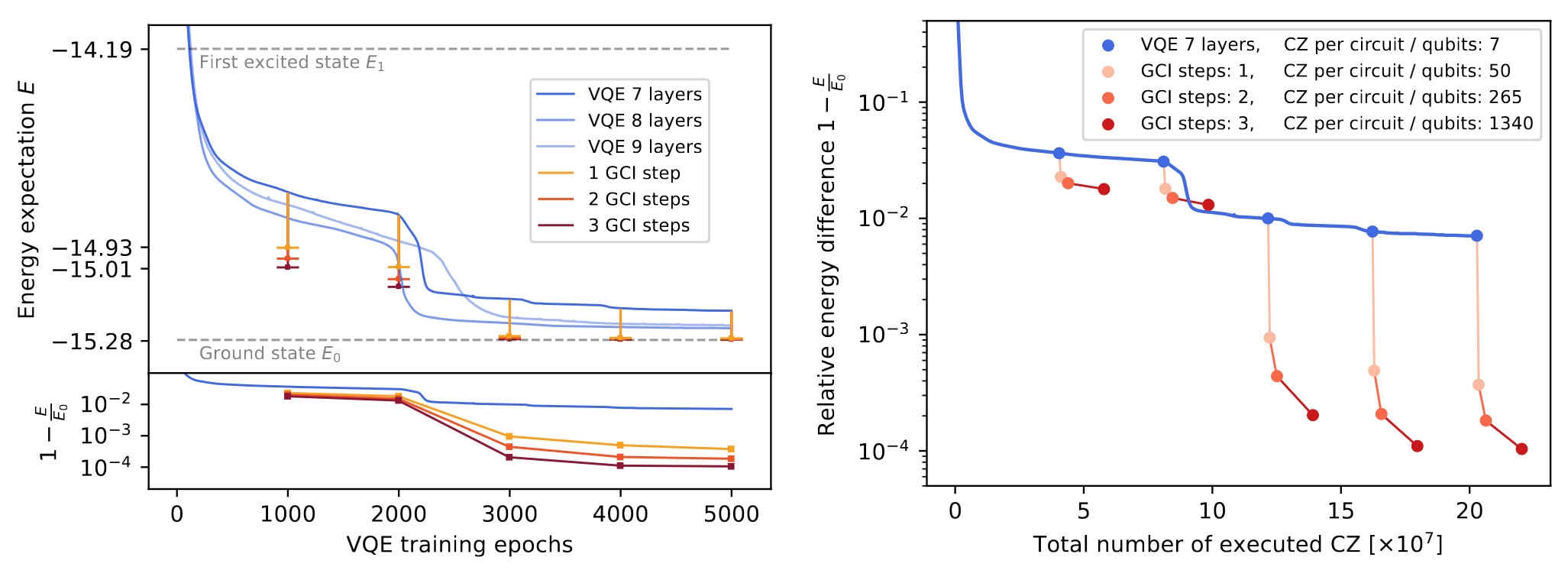
This both works and is efficient
How to interface VQE and DBQA?
Quantum Dynamic Programming
with J. Son, R. Takagi and N. Ng
QDP code structure
Warm-start unitary from variational quantum eigensolver
0
0
0
0
+
+
+
+
+
=
= U_\theta
DBQA input with warmstart
\hat A_0 \rightarrow \hat H_0 = \hat U_\theta^\dagger \hat A_0 \hat U_\theta
V_0 = e^{i\sqrt{s_0}\hat D_0}e^{i\sqrt{s_0}\hat H_0}e^{-i\sqrt{s_0}\hat D_0}e^{-i\sqrt{s_0}\hat H_0}
V_0 = e^{i\sqrt{s_0}\hat D_0}\hat U_\theta^\dagger e^{i\sqrt{s_0}\hat A_0}\hat U_\theta
e^{-i\sqrt{s_0}\hat D_0}\hat U_\theta^\dagger e^{-i\sqrt{s_0}\hat A_0}\hat U_\theta
Use unitarity and get circuit VQE insertions
10 qubit, 50 layers of CNOT - 99.5% ground state fidelity
\hat A_0 = \sum_{j=1}^L(X_j X_{j+1}+Y_j Y_{j+1}+ Z_j Z_{j+1}) \equiv \sum_{j=1}^L\hat A_0^{(j)}
e^{-it\hat A_0} \approx \left( \prod_{j=1}^L e^{-i t\hat A_0^{(j)}/M}\right)^M
e^{-i t\hat A_0^{(j)}/M}=
=
2 qubit unitary
Canonical
Canonical
For quantum compiling we use:
- higher-order group commutators
- higher-order Trotter-Suzuki decomposition
- 3-CNOT formulas
New quantum algorithm for diagonalization
\hat H \mapsto \hat \mathcal H_\ell = \hat \mathcal U_\ell^\dagger \hat H \hat\mathcal U_\ell
\partial_\ell \hat \mathcal H_\ell = [[A(\hat \mathcal H_\ell),B(\hat \mathcal H_\ell)], \hat \mathcal H_\ell]
no qubit overheads
no controlled-unitaries
0
0
0
0
C
0
0
0
0
Simple
=
Easy
Doesn't spark joy :(
Double-bracket quantum algorithm for diagonalization
\hat H \mapsto \hat H_\ell = \hat U_\ell^\dagger \hat H \hat U_\ell
\partial_\ell \hat H_\ell = [[A(\hat H_\ell),B(\hat H_\ell)], \hat H_\ell]
new approach to preparing useful states
0
0
0
0
What else is there?
Linear programming
Matching optimization
Diagonalization
Sorting
QR decomposition
Toda flow
\partial_\ell \hat H_\ell = [[A(\hat H_\ell), B(\hat H_\ell)] , \hat H_\ell]
Double-bracket flow
Runtime-boosting heuristics
Analytical convergence analysis
Group commutator bound
Hasting's conjecture
Relation to other quantum algorithms
Code is available on Github
0
0
0
0
C
Double-bracket quantum algorithms for diagonalization
with J. Son, R. Takagi and N. Ng
\mathcal{E}^{(\mathcal{N},\rho,M)}_{QDP} \coloneqq (\mathcal{E}^{(\mathcal{N},\rho)}_{1/M})^M
Quantum dynamic programming
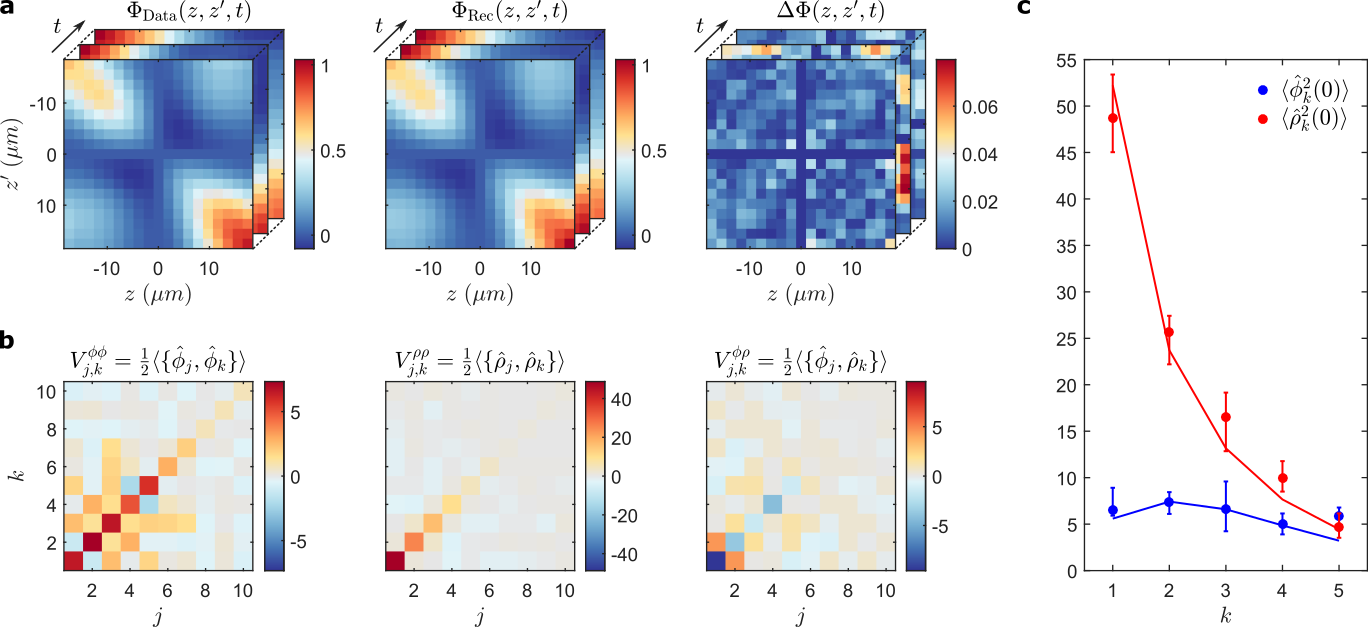
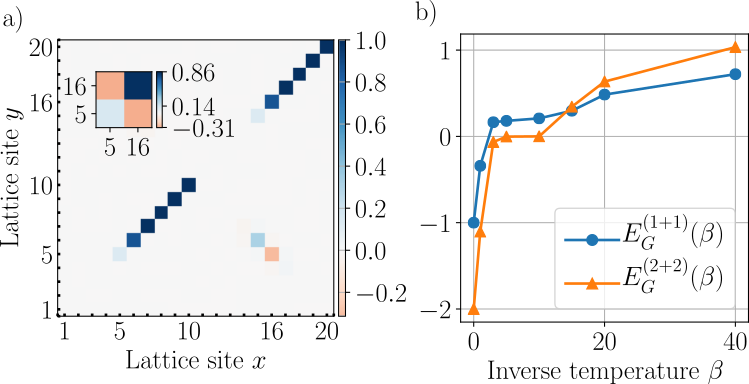
Material science?
0
0
0
0
C
How to dynamically quantum?
Group commutator
\hat H \mapsto \hat \mathcal H_\ell = \hat \mathcal U_\ell^\dagger \hat H \hat\mathcal U_\ell
\partial_\ell \hat \mathcal H_\ell = [[A(\hat \mathcal H_\ell),B(\hat \mathcal H_\ell)], \hat \mathcal H_\ell]
0
0
0
0
Want
\hat H_1 = e^{s \hat W_1} \hat H e^{-s \hat W_1}
\hat W_1 = [\Delta(\hat H),\sigma(\hat H)]
e^{is\Delta(\hat H)}e^{is\hat H}e^{-is\Delta(\hat H)}e^{-is\hat H}= e^{-s^2[\Delta(\hat H),\sigma(\hat H)]} +\hat E^\text{(GC)}
New bound
\|\hat E^\text{(GC)}\| \le 4\|\hat H\|\,\|[\Delta(\hat H),\sigma(\hat H)]\| s^3
Group commutator
\hat H \mapsto \hat \mathcal H_\ell = \hat \mathcal U_\ell^\dagger \hat H \hat\mathcal U_\ell
\partial_\ell \hat \mathcal H_\ell = [[A(\hat \mathcal H_\ell),B(\hat \mathcal H_\ell)], \hat \mathcal H_\ell]
0
0
0
0
Want
\hat H_1 = e^{s \hat W_1} \hat H e^{-s \hat W_1}
\hat W_1 = [\Delta(\hat H),\sigma(\hat H)]
e^{is\Delta(\hat H)}e^{is\hat H}e^{-is\Delta(\hat H)}e^{-is\hat H}= e^{- s^2[\Delta(\hat H),\sigma(\hat H)]} +\hat E^\text{(GC)}
How to get ?
\hat D_s(\hat H) \approx e^{is\Delta(\hat H)}
\hat C_s(\hat J) = \hat D_{\sqrt{s}}(\hat J)^\dagger \; e^{i\sqrt{s}\hat J}\; \hat D_{\sqrt{s}}(\hat J)\; e^{-i\sqrt{s}\hat J}
\approx e^{-s \hat W(\hat J)}
1,
1,
1,
1,
0,
0,
0,
0
Phase flip unitaries
\mu = (
)
N
S
N
S
N
S
N
S
\hat Z
\mathbb 1
\mathbb 1
\otimes
\otimes
\otimes
\otimes
\otimes
\otimes
\otimes
\hat Z
\hat Z
\hat Z
\mathbb 1
\mathbb 1
0,
1,
0,
1,
0,
0,
0,
1
\mu = (
)
1
\otimes
\mathbb 1
\otimes
\mathbb 1
\otimes
\hat Z
\otimes
1
\otimes
\mathbb 1
\otimes
\hat Z
\otimes
\hat Z
N
S
N
S
N
S
Phase flip unitaries
Evolution under dephased generators
\hat H \mapsto \hat H_\ell = \hat U_\ell^\dagger \hat H \hat U_\ell
\partial_\ell \hat H_\ell = [[A(\hat H_\ell),B(\hat H_\ell)], \hat H_\ell]
0
0
0
0
\hat Z_\mu e^{-i s \hat J} \hat Z_\mu = e^{-is \hat Z_\mu \hat J\hat Z_\mu}
\hat D_s(\hat J) \approx \prod_{\mu\in R} \hat Z_\mu e^{-i s \hat J/D} \hat Z_\mu
We can make it efficient:
\Delta(\hat J)= \frac 1 {\dim (\hat J)} \sum_{\mu\in\{0,1\}^{\times L}} \hat Z_\mu \hat J \hat Z_\mu
R \subseteq \{0,1\}^{\times L}
Use unitarity
and repeat many times
New quantum algorithm for diagonalization
\hat H \mapsto \hat \mathcal H_\ell = \hat \mathcal U_\ell^\dagger \hat H \hat\mathcal U_\ell
\partial_\ell \hat \mathcal H_\ell = [[A(\hat \mathcal H_\ell),B(\hat \mathcal H_\ell)], \hat \mathcal H_\ell]
0
0
0
0
\hat D_s(\hat J) = \prod_{\mu\in\{0,1\}^{\times L}} \hat Z_\mu e^{-i s \hat J/D} \hat Z_\mu
\hat C_s(\hat J) = \left( \hat D_{\sqrt{2s/K}}(\hat J)^\dagger \;e^{i\sqrt{2s/K}\hat J}\;\hat D_{\sqrt{2s/K}}(\hat J)\;e^{-i\sqrt{2s/K}\hat J}\right)^K
\hat V_k = \hat V_{k-1}\hat C_s(\hat J_{k-1})
\hat J_{k-1} = \hat V_{k-1}^\dagger \hat H \hat V_{k-1}
1) Dephasing
2) Group commutator
3) Frame shifting
\partial_\ell \hat \mathcal H_\ell = [[A(\hat \mathcal H_\ell),B(\hat \mathcal H_\ell)], \hat \mathcal H_\ell]
\hat V_k = \hat C_s(\hat J_{1})\; \hat C_s(\hat J_{2})\ldots \hat C_s(\hat J_{k-1}) \approx e^{-s \hat W_1}\;e^{-s \hat W_2}\ldots e^{-s \hat W_{k-1}}
Version 2025: Double-bracket quantum algorithms
By Marek Gluza
