New quantum algorithms based on Riemannian optimization
Marek Gluza
NTU Singapore
Scan QR code or go to slides.com/marekgluza
Watch on youtube: https://www.youtube.com/watch?v=PLVkuqPemVs
Marek Gluza
The double-bracket quantum algorithms roadmap
I grew up around these mountains where Poland meets Czech Republic and Slovakia (in Europe)
June '22: Single-author double-bracket proposal
This talk is an overview of 4 years of my research on double-bracket quantum algorithms:
- Never worked on quantum algorithms before \(\rightarrow\) 9 papers, 1 experiment
- Never participated in a research program \(\rightarrow\) lead a collaboration of 25 co-authors
- It was the mathematical observations guiding us \(\rightarrow\) Riemannian geometry is key!
[1]
[9]
[8]
[5]
[2]
[3,4]
[6]
[7]
Click these links at slides.com/marekgluza
October '21: Arrived to Singapore
Marek Gluza
The double-bracket quantum algorithms roadmap
...the outline of the talk
Today, I will tell you about double-bracket quantum algorithms
Part 1:
- What are quantum algorithms?
- What is quantum computing?
Part 3:
- What can they be used for?
- What are good tasks for quantum computers?
Part 2:
- Riemannian geometry of the unitary group
Part 4: Just basic properties of the unitary group facilitate quantum algorithm design
What is a quantum computer?
It is a quantum system e.g. ionized atom, loop of a superconductor
|
|
|
|---|---|
|
|
|
|
|
|
|
|
|
|
|
J. Leonard (TU Vienna) pointing where neutral atoms will be trapped
R. Dumke and S. Carrazza discussiong the CQT lab
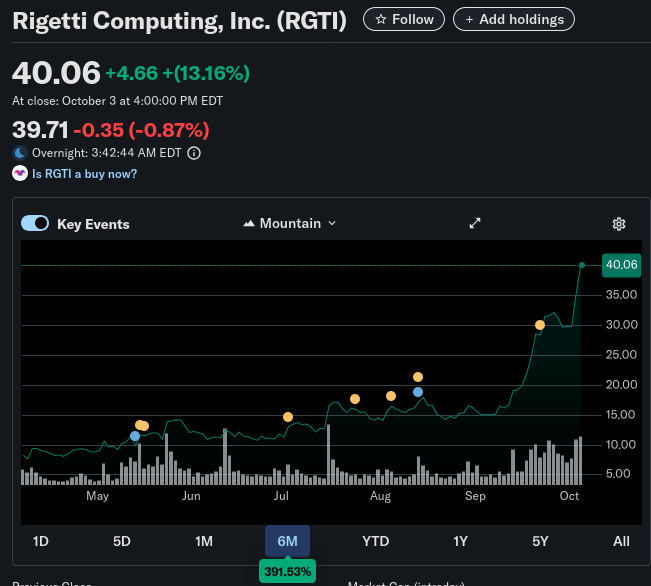
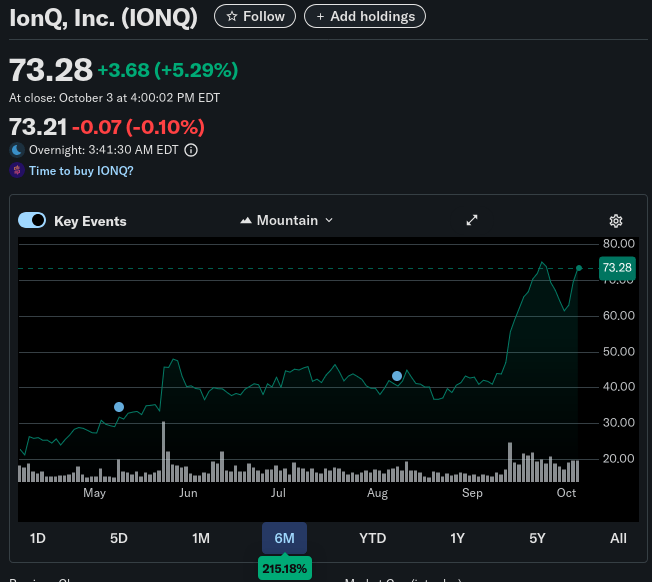
Some investors speculate their money on it - RGTI, IONQ...
We can make it!
What is a quantum computer?
It is a quantum system e.g. ionized atom, loop of a superconductor
It is modeled by a finite dimensional vector space \(\mathcal V = \mathbb C^d\)
It is modular: We can add more of its components and make \(d\) grow
It is programmable: There are ways (quantum gates) to change its states in a reproducible and reversible manner
It is universal: Composing sufficiently many of the programmable operations allows to approximate any \(v = |v\rangle \in \mathcal V\)
We take more qubits
Apply patterned EM radiation
Reproducible: Use FPGA
Reversible: Physics challenge; keep cold
Physics papers from the 90's
|
|
|
|---|---|
|
|
|
|
|
|
|
|
|
|
|
We can make it!
We take \(n\) qubits then \(\mathcal V = (\mathbb C^2)^{\otimes n}\) and \(d=2^n\)
What is a quantum computer?
It is a quantum system e.g. ionized atom, loop of a superconductor
It is modeled by a finite dimensional vector space \(\mathcal V = \mathbb C^d\)
It is modular: We can add more of its components and make \(d\) grow
It is programmable: There are ways (quantum gates) to change its states in a reproducible and reversible manner
It is universal: Composing sufficiently many of the programmable operations allows to approximate any \(|v\rangle \in \mathcal V\)
We take more qubits
Apply patterned EM radiation
Reproducible: Use FPGA
Reversible: Physics challenge; keep cold
|
|
|
|---|---|
|
|
|
|
|
|
|
|
|
|
|
We can make it!
We take \(n\) qubits then \(\mathcal V = (\mathbb C^2)^{\otimes n}\) and \(d=2^n\)
Physics papers from the 90's
For good or for worse quantum computing is influenced by physics...
What is a quantum algorithm?
0
0
0
0
C
What is a quantum computer?
It's an experimental setup A which includes a quantum system B and that setup A allows to manipulate the quantum state of B. This is modeled by mulitplying unitary matrices to vectors from a finite-dimensional vector space.
(This monumental structure is the insides of the dilution refrigerator shielding qubits from noise)
A - basket
B - fruits
Cat - noise
A - quantum computer
B - qubits
C - noise
What is a quantum computer?
A quantum computer is an experimental setup A which includes a quantum system B and that setup A allows to manipulate the quantum state of B.
Types of quantum computers:
- A) Superconducting loops
- B) Ionized atoms
- C) Neutral atoms
- D) Others
Companies:
- A) Google, IQM, IBM, Rigetti
- B) Quantinuum, IonQ
- C) Quera, Atom Computing, Pasqal
- D) Alice&Bob, Qolab, Normal Computing, Psi-Quantum,
Zapata
Currently 80 companies listed here:
https://thequantuminsider.com/2025/09/23/top-quantum-computing-companies/
Braket notation
|\psi\rangle = a | 0 \rangle + b | 1\rangle
\langle \vec v,\vec w\rangle \leftrightarrow \langle \phi|\psi\rangle
1 qubit:
*The biography of the physicist who proposed it is literally called "The strangest man"
\mathcal V = \mathbb C^2 = \mathrm{span}_{\mathbb C}\{ e_1, e_2\}
| 0 \rangle :=e_1, | 1\rangle :=e_2
v \in \mathcal V \leftrightarrow |v\rangle = v_0 | 0 \rangle + v_1 | 1\rangle
\langle \vec v,A \vec v\rangle \leftrightarrow \langle \psi|H|\psi\rangle
A \vec v \leftrightarrow H|\psi\rangle
*Dirac was one of the smartest quantum physicist in history
\vec v^\dagger \in \mathcal V^* \leftrightarrow \langle \psi|
"ket"
"bra"
"bracket"
"quantum superposition"
What is a universal quantum computer?
|\psi\rangle = a | 0 \rangle + b | 1\rangle
|\psi\rangle = a | 00 \rangle + b | 10\rangle+c | 01 \rangle + b | 11\rangle
|\psi\rangle = a | 000 \rangle + b | 100\rangle+c | 010 \rangle + d | 100\rangle+
e | 011 \rangle + f | 101\rangle+g | 110 \rangle +h | 111\rangle
|\psi\rangle = a | 0000 \rangle + b | 1000\rangle+c | 0100 \rangle + d | 1000\rangle+
e | 0011 \rangle + f | 0101\rangle+g | 1010 \rangle +h | 1100\rangle + \ldots
1 qubit
2 qubits
3 qubits
4 qubits
|\psi\rangle = U |00\ldots0\rangle \Rightarrow U \approx U_c
it can approximate any state preparation via circuits
It is a machine for realizing such linear combinations in nature
0
0
0
0
C
Operating a quantum computer is all about the group of unitary matrices
M,M' \in U(d) \Rightarrow (M M')(MM')^\dagger = M (M'M'^\dagger) M^\dagger
= M M^\dagger = I
\Rightarrow (M M')\in U(d)
\ket{\psi'} = M \ket\psi \Rightarrow \ket{\psi''} = M'\ket{\psi'} = M'M \ket\psi
Think of rotations on a sphere
U(d) = \{ M\in \mathbb C^{d\times d}: M^{-1} = M^\dagger\}
|\psi'\rangle
|\psi\rangle
|\psi''\rangle
|\psi\rangle = U |00\ldots0\rangle
Operating a quantum computer is all about the group of unitary matrices
\exist G_1,G_2,\ldots G_K \in U(d) \mathrm{~such~that}
Think of rotations on a sphere
Universal quantum computation means: Composing sufficiently many basic unitary matrices (elementary quantum gates \(G_1,G_2,\ldots, G_K\)) can approximate any other 'larger' unitary.
(finding these sequences = task of unitary synthesis)
U(d) = \{ M\in \mathbb C^{d\times d}: M^{-1} = M^\dagger\}
\forall M \in U(d)~\exist \mathrm{sequence~s.t.} ~M\approx G_1 G_5G_6G_1 G_K G_1 G_2\ldots
Marek Gluza
The double-bracket quantum algorithms roadmap
...the outline of the talk
Today, I will tell you about double-bracket quantum algorithms
Part 1:
- What are quantum algorithms?
- What is quantum computing?
Part 3:
- What can they be used for?
- What are good tasks for quantum computers?
Part 2:
- Riemannian geometry of the unitary group
Part 4: Just basic properties of the unitary group facilitate quantum algorithm design
Next: Why a watermelon?
This visualizes the operations on a quantum computer
(Riemannian geometry)
- Riemannian geometry is a generalization of the geometry of the sphere
- For 1 qubit the sphere is a great model of quantum operations
- In higher dimensions many parallels remain e.g. set of quantum operations is compact (the watermelon fits into the hand) but many get lost e.g. non-convex submanifolds (green colors on the watermelon)
- If watermelon is placed on the table then the table is tangent to it
This visualizes the operations on a quantum computer
(Riemannian geometry)
- Riemannian geometry is a generalization of the geometry of the sphere
- For 1 qubit the sphere is a great model of quantum operations
- In higher dimensions many parallels remain e.g. set of quantum operations is compact (the watermelon fits into the hand) but many get lost e.g. non-convex submanifolds (green colors on the watermelon)
- If watermelon is placed on the table then the table is tangent to it
Next: Let's see how to use geometry to design quantum algorithms
Riemannian geometry is essential for quantum computation
- The unitary group \(U(d)\) is a Riemannian manifold
- It is an embedded manifold \(U(d) = \{M\in \mathbb C^{d\times d}:~M^{-1}=M^\dagger\}\)
- The tangent space is \(\{W\in \mathbb C^{d\times d}:~W^{\dagger}= -W\} \simeq\{iH \mathrm{~where~} H=H^\dagger\in \mathbb C^{d\times d}\} \)
- The geodesics are matrix exponentials \( \{e^{sW}\}_{s\in\mathbb R} \subset U(d)\) or \( \{e^{isH}\}_{s\in\mathbb R} \subset U(d)\)
- Computing a "gradient" must output an element of the tangent space
\mathbb C^{d\times d}
U(d)
g
W
iH
g^\dagger = -g
e^{s g}
g
g^\dagger = -g
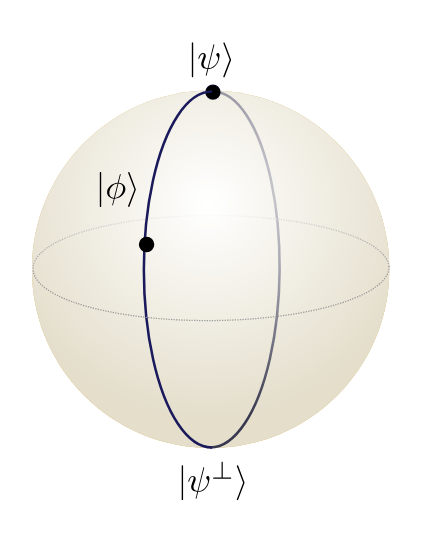
\(\partial_{i,j}\) points to the interior, not tangential
Keep this in mind for later: Unlike in flat space, these 4 steps spiral away from the point of origin
Riemannian geometry is essential for quantum computation
- The unitary group \(U(d)\) is a Riemannian manifold
- The tangent space is \(\{H\in \mathbb C^{d\times d}:~H^{\dagger}= H\} \)
- The geodesics are matrix exponentials \( \{e^{isH}\}_{s\in\mathbb R} \subset U(d)\)
- \(U(d)\) is a curved manifold
e^{is A}e^{is B}e^{-is A}e^{-is B} \neq 1
e^{is A}
e^{isB}
e^{-isB}
e^{-is A}
Operating a quantum computer is all about the group of unitary matrices
\forall A=A^\dagger, B=B^\dagger: ~~M = e^{ [A,B]}\in U(d)
Think of rotations on a sphere
The Lie bracket of two 'velocities' is again a velocity:
Check: \([A,B]^\dagger = (AB- BA)^\dagger = B^\dagger A^\dagger -A^\dagger B^\dagger = -[A,B]\)
M^\dagger = (e^{ [A,B]})^\dagger = e^{ [A,B]^\dagger}=e^{ -[A,B]}=M^{-1}
U(d)
e^{ [A,B]}
\([A,B]^\dagger = -[A,B]\)
Check: \([A,B]^\dagger = -[A,B]\)
U(d) = \{ M\in \mathbb C^{d\times d}: M^{-1} = M^\dagger\}
Operating a quantum computer is all about the group of unitary matrices
\forall A=A^\dagger, B=B^\dagger: ~~M = e^{ [A,B]}\in U(d)
Think of rotations on a sphere
Fact 3: The Lie bracket of two 'velocities' is again a velocity
U(d) = \{ M\in \mathbb C^{d\times d}: M^{-1} = M^\dagger\}
e^{isA}e^{isB}e^{-isA}e^{-isB} = e^{-s^2[A,B]}+O(s^3)
e^{is A}
e^{isB}
e^{-isB}
e^{-is A}
Operating a quantum computer is all about the group of unitary matrices
U(d) = \{ M\in \mathbb C^{d\times d}: M^{-1} = M^\dagger\}
Think of rotations on a sphere
Fact 3: The Lie bracket of two 'velocities' is again a velocity
My quantum algorithms use such unitary matrices - they are implementing Riemannian gradient descent
e^{isA}e^{isB}e^{-isA}e^{-isB} = e^{-s^2[A,B]}+O(s^3)
\forall A=A^\dagger, B=B^\dagger: ~~M = e^{ [A,B]}\in U(d)
The main tool of double-bracket quantum algorithms
e^{is A}
e^{isB}
e^{-isB}
e^{-is A}
Marek Gluza
Marek Gluza
The double-bracket quantum algorithms roadmap
...the outline of the talk
Today, I will tell you about double-bracket quantum algorithms
Part 1:
- What are quantum algorithms?
- What is quantum computing?
Part 3:
- What can they be used for?
- What are good tasks for quantum computers?
Part 2:
- Riemannian geometry of the unitary group
Part 4: Just basic properties of the unitary group facilitate quantum algorithm design
4 stages of creating quantum algorithms
1. Design choice:
How to go about it?
|\psi(\tau)\rangle = \frac{e^{-\tau H}|\psi\rangle}{\| e^{-\tau H}|\psi\rangle\|}
2. Unitary synthesis:
How to do it?
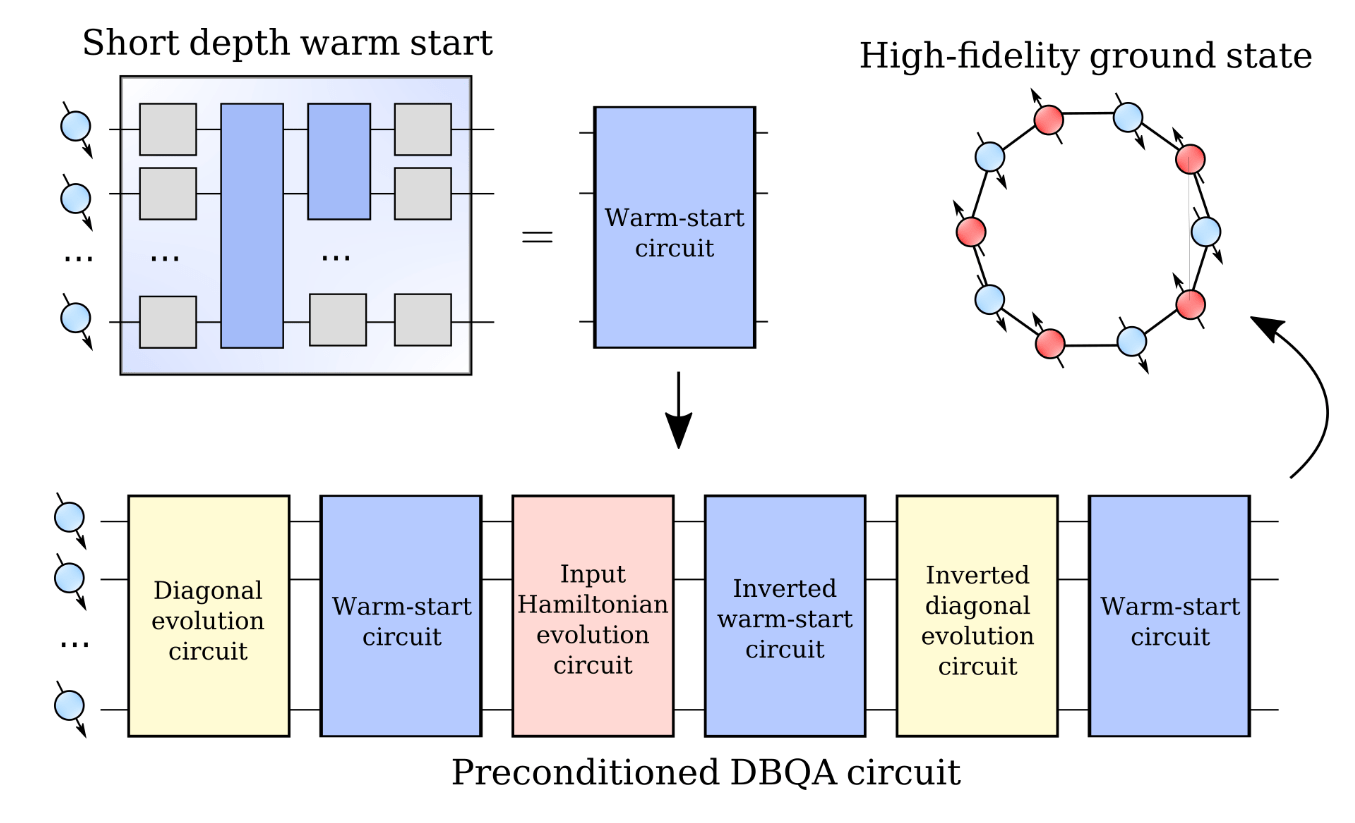
3. Circuit compilation:
What gates to do?
0. Problem choice:
What challenge to take up?
Double-bracket quantum algorithms:
Systematic framework for unitary synthesis
Quantum computing cannot be useful if
- The problem can be solved quickly on classical computers
- Solving the problem isn't important
- Solving the problem is too hard for the quantum computer
Examples
- Trade bonding?
- Random sampling
- Mixed-integer programming? Shortest-vector problem? Etc.
Classical computation
Difficult, important and doable problem
Millenials
What challenge to take up?
0. Problem choice:
What challenge to take up?
Materials science?
Quantum computing cannot be useful if
- The problem can be solved quickly on classical computers
- Solving the problem isn't important
- Solving the problem is too hard for the quantum computer
Examples
- Trade bonding?
- Random sampling
- Mixed-integer programming? Shortest-vector problem? Etc.
When a lot of people can gain by having something to say, some will not resist the temptation to speak without having much to tell which creates hype
How to go about designing quantum algorithms?
- Now: Not many distinct quantum algorithms
https://quantumalgorithmzoo.org/ - Why?
- 00's Shor: Why have not more algorithms been found?
https://cs.brynmawr.edu/Courses/cs380/fall2012/Shor2003.pdf
Either because the easy ones are efficient classically or we have no good language
- Classically: Reduction to decision problems
- Quantumly: Is \(\langle\psi|H|\psi\rangle\) lower than ...?
- Optimization: Only quadratic speed-up?
Click links at slides.com/marekgluza
- 90's Shor: quantum computers can break cryptography
E(\psi) = \langle \psi| H | \psi\rangle
="\overline{v}^\top H v"
Why materials science? Imagine improving photovoltaics by 1%.
What needs to be done? Perform \(\bra\psi H\ket\psi\) optimization.
How? Quantum circuit synthesis.
This is worth being hyped!
Materials science?
Riemannian geometry leads to quantum algorithms
Next: How to get $$ from a quantum computer?
We need to optimize among all operations of the quantum computer to get a low-energy state
(Riemannian optimization)
E(\psi) = \langle \psi| H | \psi\rangle
Marek Gluza
The double-bracket quantum algorithms roadmap
...the outline of the talk
Today, I will tell you about double-bracket quantum algorithms
Part 1:
- What are quantum algorithms?
- What is quantum computing?
Part 3:
- What can they be used for?
- What are good tasks for quantum computers?
Part 2:
- Riemannian geometry of the unitary group
Part 4: Just basic properties of the unitary group facilitate quantum algorithm design
E(\psi) = \langle \psi| H | \psi\rangle
| \psi\rangle \mapsto e^{is A}|\psi\rangle
Note that choosing \(A=H\) doesn't change the energy
E(\psi') = \langle \psi| e^{-is H} He^{isH} | \psi\rangle = E(\psi)
Let's find which directions \(A\) are more useful!
\(\partial_{i,j}\) points to the interior, not tangential so which direction is best?
g
W
iH
iA
Riemannian gradient: Unique vector \(g\) in the tangent space
such that the directional derivative is a projection onto \(g\)
\nabla_W f(x) = \text{lim}_{s\rightarrow 0}\frac{ f(x+s W) - f(x)}{s} = \langle g, W\rangle
\(\partial_{i,j}\) points to the interior, not tangential so which direction is best?
g
W
iH
iA
Tr(ABC) = Tr(CAB)
\langle g, W\rangle_{\rm{HS}} = \mathrm{Tr}\left(g^\dagger W\right)
(|\psi\rangle\langle \psi|)^\dagger = |\psi\rangle\langle \psi|, H^\dagger = H
We will use very simple ingredients to find \(g\) for \(E(\psi) = \langle \psi| H | \psi\rangle\):
Hilbert-Schmidt scalar product:
Cyclicity of trace:
Tangent space:
Riemannian gradient: Unique vector \(g\) in the tangent space such that the directional derivative is a projection onto \(g\)
\nabla_W f(x) = \text{lim}_{s\rightarrow 0}\frac{ f(x+sW) - f(x)}{s} = \langle g, W\rangle
\nabla_A E(\psi) = \text{lim}_{s\rightarrow 0} \frac{ \langle \psi| e^{-isA}He^{isA}| \psi\rangle- \langle \psi|H | \psi\rangle}{s}
Tr(ABC) = Tr(CAB)\\
\Downarrow \\
Tr(|\psi\rangle\langle \psi| [H,A] ) = Tr([|\psi\rangle\langle \psi|,H]A)
E(\psi) = \langle \psi| H | \psi\rangle
| \psi\rangle \mapsto e^{is A}|\psi\rangle
=\partial_s \langle \psi| e^{-isA}He^{isA}| \psi\rangle_{|s=0}
= iTr\left[|\psi\rangle\langle\psi| [A,H]\right]
\nabla_W f(x) = \langle g, W\rangle
\nabla_A E(\psi) =
\langle- i[|\psi\rangle\langle \psi|,H] , A\rangle_{\rm{HS}}
\\\Downarrow\\
g \equiv -i[|\psi\rangle\langle \psi|,H]
|\psi'\rangle = e^{s[|\psi\rangle\langle \psi|,H]} |\psi\rangle
|\psi\rangle \mapsto e^{isg} |\psi\rangle
|\psi''\rangle = e^{s[|\psi'\rangle\langle \psi'|,H]} |\psi'\rangle
Double-bracket quantum algorithms:
Systematic framework for implementing exponentials of commutators on quantum computers. This uncovered new unitary synthesis formulas.
Riemannian gradient: Unique vector \(g\) in the tangent space such that the directional derivative is a projection onto \(g\)
e^{is A}
e^{isB}
e^{-isB}
e^{-is A}
Double-bracket flows
\partial_t O(t)= i[H,O(t)]
\partial_t \rho(t)= i[H,\rho(t)]
\partial_t A(t)= [A(t),[A(t),B]]
H \sim -i[A(t),B]
|
Heisenberg equation |
Linear, variable: observable |
|---|---|
|
Schroedinger equation |
Linear, variable: density matrix |
|
Double-bracket flow |
Non-linear, variable: density matrix or observable The solution is a unitary rotation because |
Why double a bracket?
\partial_t \hat A(t) = i [ \hat H(t), \hat A(t)]
\partial_t \hat A(t) = [ \hat H(t), [\hat H(t), \hat A(t)]]
=
2 qubit unitary
Canonical
\partial_t \hat A(t) = [ \hat A(t), [\hat A(t), \hat B]]
Double-bracket quantum algorithms
are inspired by double-bracket flows
and allow to perform optimization through short quantum computations
4 stages of creating quantum algorithms
1. Design choice:
How to go about it?
|\psi(\tau)\rangle = \frac{e^{-\tau H}|\psi\rangle}{\| e^{-\tau H}|\psi\rangle\|}
2. Unitary synthesis:
How to do it?
3. Circuit compilation:
What gates to do?
0. Problem choice:
What challenge to take up?
We need an optimization solver, i.e. we need to find ways to lower \(\bra\psi H\ket \psi\)
4 stages of creating quantum algorithms
A crisis in quantum algorithm design:
Will quantum computers be fast?
1. Design choice:
How to go about it?
|\psi(\tau)\rangle = \frac{e^{-\tau H}|\psi\rangle}{\| e^{-\tau H}|\psi\rangle\|}
2. Unitary synthesis:
How to do it?
3. Circuit compilation:
What gates to do?
0. Problem choice:
What challenge to take up?
Adiabatic "QAOA" approach:
Slowly change the Hamiltonian to "quantumly" tunnel into the solution - not fast enough see e.g. arxiv:2510.06337
Journalist questions vs. hype:
- What was done?
- Where are its limitations?
- Why is it faster?
(Pros and cons of heuristics)
1. Design choice:
How to go about it?
|\psi(\tau)\rangle = \frac{e^{-\tau H}|\psi\rangle}{\| e^{-\tau H}|\psi\rangle\|}
2. Unitary synthesis:
How to do it?
3. Circuit compilation:
What gates to do?
0. Problem choice:
What challenge to take up?
Double-bracket quantum algorithms are guaranteed to converge. They can pick-up after learning of an optimized circuit has gotten stuck.
Brute-force idea:
Select geodesic directions and learn how long step lengths - will get stuck arxiv:1803.11173
See Nature Comm. referee reports of arxiv:1803.11173
A crisis in quantum algorithm design:
Will quantum computers be fast?
S. Carrazza
August '24: Very few!
August '23: Maybe few?
Game changer - NTU's PPF 200k grant came in: Travel and hire
How many quantum gates are needed?
(Pros and cons of heuristics)
Marek Gluza
The double-bracket quantum algorithms roadmap
...the outline of the talk
Today, I will tell you about double-bracket quantum algorithms
Part 1:
- What are quantum algorithms?
- What is quantum computing?
Part 3:
- What can they be used for?
- What are good tasks for quantum computers?
Part 2:
- Riemannian geometry of the unitary group
Part 4: Just basic properties of the unitary group facilitate quantum algorithm design
4 stages of creating quantum algorithms
1. Design choice:
How to go about it?
|\psi(\tau)\rangle = \frac{e^{-\tau H}|\psi\rangle}{\| e^{-\tau H}|\psi\rangle\|}
3. Circuit compilation:
What gates to do?
0. Problem choice:
What challenge to take up?
2. Unitary synthesis:
How to do it?
Double-bracket quantum algorithms:
Systematic framework for unitary synthesis
4 stages of creating quantum algorithms
4 stages of creating quantum algorithms
1. Design choice:
How to go about it?
|\psi(\tau)\rangle = \frac{e^{-\tau H}|\psi\rangle}{\| e^{-\tau H}|\psi\rangle\|}
3. Circuit compilation:
What gates to do?
|\psi(\tau)\rangle = \frac{e^{-\tau H}|\psi\rangle}{\| e^{-\tau H}|\psi\rangle\|}
0. Problem choice:
What challenge to take up?
2. Unitary synthesis:
How to do it?
4 stages of creating quantum algorithms
Imaginary-time evolution
4 stages of creating quantum algorithms
1. Design choice:
How to go about it?
|\psi(\tau)\rangle = \frac{e^{-\tau H}|\psi\rangle}{\| e^{-\tau H}|\psi\rangle\|}
3. Circuit compilation:
What gates to do?
|\psi(\tau)\rangle = \frac{e^{-\tau H}|\psi\rangle}{\| e^{-\tau H}|\psi\rangle\|}
0. Problem choice:
What challenge to take up?
2. Unitary synthesis:
How to do it?
|\psi(\tau)\rangle = \frac{e^{-\tau H}|\psi\rangle}{\| e^{-\tau H}|\psi\rangle\|}
= e^{\tau[|\psi\rangle\langle\psi|,H]}|\psi\rangle +O(\tau^2)
4 stages of creating quantum algorithms
4 stages of creating quantum algorithms
\frac{e^{-\tau H}|\psi\rangle}{\| e^{-\tau H}|\psi\rangle\|}
= e^{\tau[|\psi\rangle\langle\psi|,H]}|\psi\rangle +O(\tau^2)
Product formula approximation:
\(e^{\tau[|\psi\rangle\langle\psi|,H]} = e^{i\sqrt{\tau}H}e^{i\sqrt{\tau}|\psi\rangle\langle\psi|}e^{-i\sqrt{\tau}H}e^{-i\sqrt{\tau}|\psi\rangle\langle\psi|} + O(\tau^{3/2})\)
4 stages of creating quantum algorithms
2. Unitary synthesis:
How to do it?
1. Design choice:
How to go about it?
|\psi(\tau)\rangle = \frac{e^{-\tau H}|\psi\rangle}{\| e^{-\tau H}|\psi\rangle\|}
3. Circuit compilation:
What gates to do?
|\psi(\tau)\rangle = \frac{e^{-\tau H}|\psi\rangle}{\| e^{-\tau H}|\psi\rangle\|}
0. Problem choice:
What challenge to take up?
= e^{i\sqrt{\tau}H}e^{i\sqrt{\tau}|\psi\rangle\langle\psi|}e^{i\sqrt{\tau}H}|\psi\rangle + O(\tau^{3/2})
Product formula approximation:
\(e^{\tau[|\psi\rangle\langle\psi|,H]} = e^{i\sqrt{\tau}H}e^{i\sqrt{\tau}|\psi\rangle\langle\psi|}e^{-i\sqrt{\tau}H}e^{-i\sqrt{\tau}|\psi\rangle\langle\psi|} + O(\tau^{3/2})\)
Quantum algorithm DB-QITE - iterate recursively:
- Define \(|{\psi_k}\rangle = U_k |0\rangle\)
- Use \(e^{is |\psi_k\rangle\langle\psi_k|} = U_ke^{is |0\rangle\langle0|}U_k^\dagger \)
- Recursively iterate \( U_{k+1} = e^{is H} U_k e^{is |0\rangle\langle 0|} U_k^\dagger e^{-is H} U_k\)
3 stages of creating quantum algorithms
1. Design choice:
How to go about it?
3. Circuit compilation:
What gates to do?
|\psi(\tau)\rangle = \frac{e^{-\tau H}|\psi\rangle}{\| e^{-\tau H}|\psi\rangle\|}
0. Problem choice:
What challenge to take up?
e^{itH}\\
e^{it|\psi\rangle\langle\psi|}
4 stages of creating quantum algorithms
2. Unitary synthesis:
How to do it?
(accepted at PRL)
Product formula approximation:
\(e^{\tau[|\psi\rangle\langle\psi|,H]} = e^{i\sqrt{\tau}H}e^{i\sqrt{\tau}|\psi\rangle\langle\psi|}e^{-i\sqrt{\tau}H}e^{-i\sqrt{\tau}|\psi\rangle\langle\psi|} + O(\tau^{3/2})\)
Quantum algorithm DB-QITE - iterate recursively:
- Define \(|{\psi_k}\rangle = U_k |0\rangle\)
- Use \(e^{is |\psi_k\rangle\langle\psi_k|} = U_ke^{is |0\rangle\langle0|}U_k^\dagger \)
- Recursively iterate \( U_{k+1} = e^{is H} U_k e^{is |0\rangle\langle 0|} U_k^\dagger e^{-is H} U_k\)
3 stages of creating quantum algorithms
1. Design choice:
How to go about it?
3. Circuit compilation:
What gates to do?
|\psi(\tau)\rangle = \frac{e^{-\tau H}|\psi\rangle}{\| e^{-\tau H}|\psi\rangle\|}
0. Problem choice:
What challenge to take up?
e^{itH}\\
e^{it|\psi\rangle\langle\psi|}
4 stages of creating quantum algorithms
2. Unitary synthesis:
How to do it?
(accepted at PRL)
Numerical results for DB-QITE:
DB-QITE:
- Define \(|{\psi_k}\rangle = U_k |0\rangle\)
- Recursively iterate \( U_{k+1} = e^{is H} U_k e^{is |0\rangle\langle 0|} U_k^\dagger e^{-is H} U_k\)
Then:
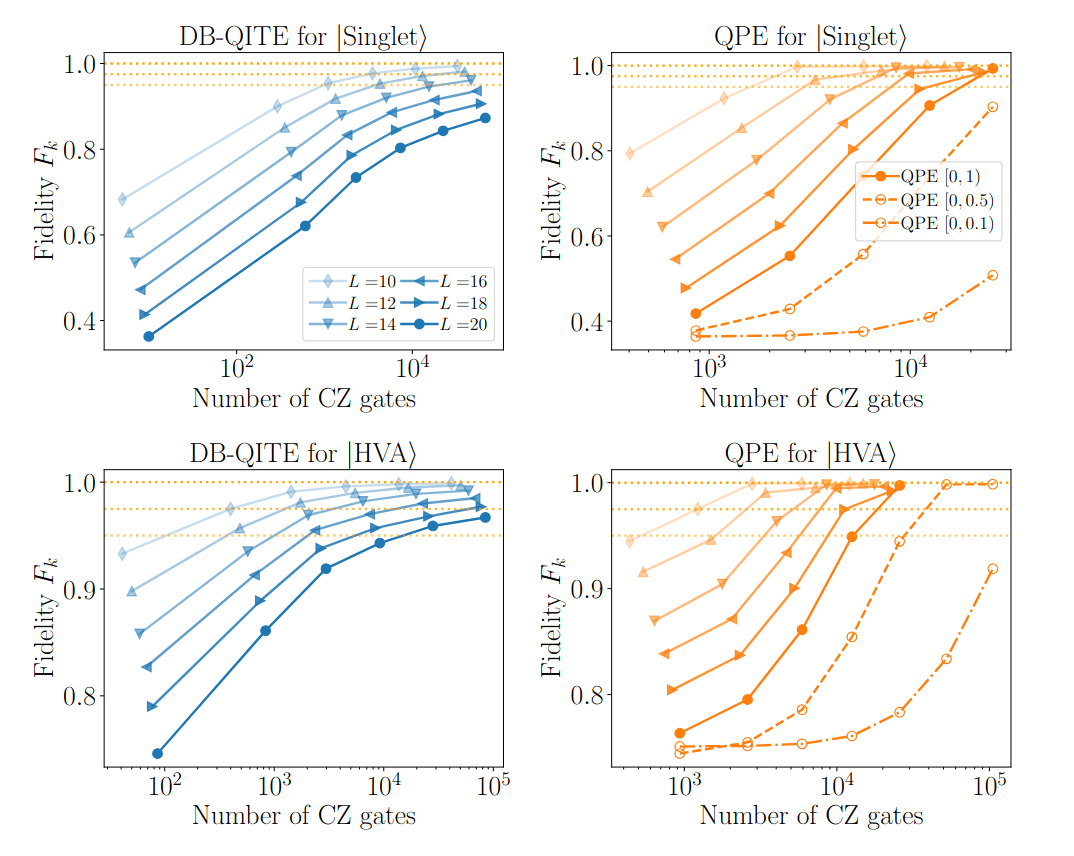
Quantinuum
(accepted at PRL)
4 stages of creating quantum algorithms
1. Design choice:
How to go about it?
|\psi(\tau)\rangle = \frac{e^{-\tau H}|\psi\rangle}{\| e^{-\tau H}|\psi\rangle\|}
2. Unitary synthesis:
How to do it?
3. Circuit compilation:
What gates to do?
0. Problem choice:
What challenge to take up?
Double-bracket quantum algorithms:
Systematic framework for unitary synthesis
4 stages of creating quantum algorithms
Double-bracket quantum algorithms
Click these links at slides.com/marekgluza
| Diagonalization | https://arxiv.org/abs/2206.11772 | ||
|---|---|---|---|
| Imaginary-time evolution | https://arxiv.org/abs/2412.04554 | ||
| Quantum signal processing | https://arxiv.org/abs/2504.01077 | ||
| Grover's search | https://arxiv.org/abs/2507.15065 | Approximates ITE |
U^\dagger H U =
\begin{pmatrix}
\lambda_0&&\\
&\lambda_1&\\
&&\ddots
\end{pmatrix}
|\psi(\tau)\rangle = \frac{e^{-\tau H}|\psi\rangle}{\| e^{-\tau H}|\psi\rangle\|}
\frac{ \prod_{k=1}^K(H-z_k I)|\psi\rangle}{\| \prod_{k=1}^K(H-z_k I)|\psi\rangle\|}
\prod_{k=1}^Ke^{i\theta_k|\psi_k\rangle\langle\psi_k|} e^{s_k[|\psi_k\rangle\langle\psi_k|,H]}|\psi\rangle
H' = e^{-s[D,H]}H e^{s[D,H]}
e^{s[|\psi\rangle\langle\psi|,H]}|\psi\rangle +O(\tau^2)
(1-2|\psi\rangle\langle\psi|)\times e^{i t H_f}
e^{s[|\psi\rangle\langle\psi|,H]}|\psi\rangle
Solve the unitary synthesis problem in all these cases through Riemannian gradients!
How to go about designing quantum algorithms?
- Now: Not many distinct quantum algorithms
https://quantumalgorithmzoo.org/ - Why?
- Classically: Reduction to decision problems
- Quantumly: Is \(\langle\psi|H|\psi\rangle\) lower than ...?
- Optimization: Only quadratic speed-up?
- "Grand unification of quantum algorithms" https://arxiv.org/abs/2105.02859 the block-encoding scheme for accessing \(H\)
- This talk: Another unification based on Riemannian optimization and using geodesics \(e^{isH}\) to access \(H\)
- Double-bracket quantum algorithms give intuition why unification possible: \(\langle\psi|H|\psi\rangle\) is optimization so interpret through Riemannian gradients
Click links at slides.com/marekgluza
E(\psi) = \langle \psi| H | \psi\rangle
="\overline{v}^\top H v"
Double-bracket quantum algorithms
- Coherently implement Riemannian gradient steps
-
Give rigorous unitary synthesis for
- imaginary-time evolution
- quantum signal processing
- diagonalization unitaries
- Grover's as an approximation to imaginary-time evolution
- Training quantum circuits from data doesn't work well, unlike in classical machine learning applications. However those variational learning methods are great for warm-starting double-bracket quantum algorithms!
Tell me when not fast enough? Get stuck? Something else?
Your input is needed to improve them!
N. Ng
Z. Holmes
R. Zander
R. Seidel
Y. Suzuki
B. Tiang
J. Son
S. Carrazza
Stay in touch on LinkedIn:
Text
Text
Text
4 stages of creating quantum algorithms
1. Design choice:
How to go about it?
|\psi(\tau)\rangle = \frac{e^{-\tau H}|\psi\rangle}{\| e^{-\tau H}|\psi\rangle\|}
3. Circuit compilation:
What gates to do?
|\psi(\tau)\rangle = \frac{e^{-\tau H}|\psi\rangle}{\| e^{-\tau H}|\psi\rangle\|}
0. Problem choice:
What challenge to take up?
2. Unitary synthesis:
How to do it?
Double-bracket quantum algorithms:
Systematic framework for unitary synthesis
|\psi(\tau)\rangle = \frac{e^{-\tau H}|\psi\rangle}{\| e^{-\tau H}|\psi\rangle\|}
= e^{\tau[|\psi\rangle\langle\psi|,H]}|\psi\rangle +O(\tau^2)
|\psi(\tau)\rangle = \frac{e^{-\tau H}|\psi\rangle}{\| e^{-\tau H}|\psi\rangle\|} \\
= e^{\tau[|\psi\rangle\langle\psi|,H]}|\psi\rangle +O(\tau^2)\\
= e^{i\sqrt{\tau}H}e^{i\sqrt{\tau}|\psi\rangle\langle\psi|}e^{i\sqrt{\tau}H}|\psi\rangle + O(\tau^{3/2})
e^{itH}\\
e^{it|\psi\rangle\langle\psi|}
Product formula approximation:
\(e^{\tau[|\psi\rangle\langle\psi|,H]}| = e^{i\sqrt{\tau}H}e^{i\sqrt{\tau}|\psi\rangle\langle\psi|}e^{-i\sqrt{\tau}H}e^{-i\sqrt{\tau}|\psi\rangle\langle\psi|} + O(\tau^{3/2})\)
4 stages of creating quantum algorithms
What is quantum signal processing?
|\psi'\rangle = e^{-\tau H} |\psi\rangle = \sum_k \langle\lambda_k|\psi\rangle e^{-\tau \lambda_k }|\lambda_k\rangle \rightarrow 0
|\psi'\rangle = \frac{e^{-\tau H} |\psi\rangle}{\|e^{-\tau H} |\psi\rangle\|} \rightarrow |\lambda_0\rangle
|\psi'\rangle = \frac{P(H) |\psi\rangle}{\|P(H) |\psi\rangle\|} \rightarrow |\lambda_0\rangle
P(x)=\prod_{k=1}^K(x-x_k)\approx e^{-\tau x}
|\psi'\rangle = \frac{P(H) |\psi\rangle}{\|P(H) |\psi\rangle\|} \rightarrow \frac{H^{-1}|\psi\rangle}{\|H^{-1} |\psi\rangle\|}
P(x)\approx 1/x
Example 1: Exponential function
Example 2: Polynomial approximation to exponential
Example 3: Polynomial approximation to inversion
P(H)=\prod_{k=1}^K(H-x_k)\approx e^{-\tau H}
Quantum signal processing maps between states according to a polynomial filter
|\psi'\rangle = \frac{P(H) |\psi\rangle}{\|P(H) |\psi\rangle\|}
Approach 2. Exponentials of commutators
- Recursive ~ exponentially long circuits
- Double-bracket quantum algorithms link to Riemannian gradients
Approach 1. Block-encodings
- Probablistic ~ exponentially unlikely postselection
- Grand unification of quantum algorithms https://arxiv.org/abs/2105.02859
|\psi'\rangle = \frac{P(H) |\psi\rangle}{\|P(H) |\psi\rangle\|} = U_\psi(P) |\psi\rangle
U_\psi(P)
Next:
- we will consider \(1-\tau H \approx e^{-\tau H}\)
- we will find \(U_\psi(P = 1-\tau H)\)
- discuss how to generalize to any QSP
|\psi'\rangle = \frac{P(H) |\psi\rangle}{\|P(H) |\psi\rangle\|} = U_\psi(P) |\psi\rangle
U_\psi(P)
|\psi'\rangle = \frac{P(H) |\psi\rangle}{\|P(H) |\psi\rangle\|} = U_\psi(P) |\psi\rangle
U_\psi(P)
|\phi'\rangle = e^{s[|\phi\rangle\langle\phi|,H]} |\phi\rangle
U_\phi(P) = e^{s[|\phi\rangle\langle\phi|,H]}
We will show that
\(P(H) = 1-\tau_sH\)
Ansatz:
|\psi'\rangle = e^{s[|\psi\rangle\langle \psi|,H]} |\psi\rangle
|\psi'\rangle = \sum_{n=0}^\infty \frac{s^n}{n!} ([|\psi\rangle\langle \psi|,H])^n |\psi\rangle
[|\psi\rangle\langle \psi|,H] |\psi\rangle = |\psi\rangle\langle \psi|H |\psi\rangle - H|\psi\rangle\langle \psi |\psi\rangle
[|\psi\rangle\langle \psi|,H] |\psi\rangle = (E-H) |\psi\rangle
Double-bracket ansatz:
\(n=1\):
([|\psi\rangle\langle \psi|,H])^2 |\psi\rangle = [|\psi\rangle\langle \psi|,H](E-H) |\psi\rangle
([|\psi\rangle\langle \psi|,H])^2 |\psi\rangle = E(E-H) |\psi\rangle - [|\psi\rangle\langle \psi|,H] H |\psi\rangle
= - V|\psi\rangle
([|\psi\rangle\langle \psi|,H])^{2k} |\psi\rangle = (- 1)^k V^k|\psi\rangle
([|\psi\rangle\langle \psi|,H])^{2k+1} |\psi\rangle = (- 1)^k V^k(E-H)|\psi\rangle
[|\psi\rangle\langle \psi|,H] |\psi\rangle = (E-H) |\psi\rangle
\(n=1\):
\(n=2\):
Y. Suzuki
= E^2 |\psi\rangle - EH |\psi\rangle - |\psi\rangle\langle \psi|H^2 |\psi\rangle + E H|\psi\rangle
V =\langle \psi |H^2|\psi\rangle - \langle \psi |H|\psi\rangle^2
([|\psi\rangle\langle \psi|,H])^{2k} |\psi\rangle = (- 1)^k V^k|\psi\rangle
([|\psi\rangle\langle \psi|,H])^{2k+1} |\psi\rangle = (- 1)^k V^k(E-H)|\psi\rangle
This starts looking like quantum signal processing, let's see more next.
Lemma 1. Any linear polynomial with a real root \(P(H) = 1-\tau H\) can be implemented this way.
([|\psi\rangle\langle \psi|,H])^{2k} |\psi\rangle = (- 1)^k V^k|\psi\rangle
([|\psi\rangle\langle \psi|,H])^{2k+1} |\psi\rangle = (- 1)^k V^k(E-H)|\psi\rangle
This starts looking like quantum signal processing, let's see more next.
Lemma 1. Any linear polynomial with a real root \(P(H) = 1-\tau H\) can be implemented this way.
Observation. If there is a complex root \(P(H) = H-z\) can be done by
\(U_\psi(P) = e^{i\theta |\psi\rangle\langle\psi|}e^{s[|\psi\rangle\langle\psi|,H]}\)
Result: Recursive iteration implements any QSP!
This starts looking like quantum signal processing, let's see more next.
Lemma 1. Any linear polynomial with a real root \(P(H) = 1-\tau H\) can be implemented this way.
Goals?
Realistic?
Intuition?
Quantum computer
Quantum algorithm
Cooling
Natural
0
0
0
0
C
[1] Double-bracket quantum algorithms for diagonalization
YES!!!!
Singapore's
quantum computer
R. Dumke
S. Carrazza
Optimizing a random guess to cool gets stuck
Can't do material science?! :(
DBQA moves it ahead!
[3]
We know how to make it run fast!
Quantum gates
N. Ng
Exactly how good is it?
[2]
Double-bracket quantum algorithms
- coherently implement Riemannian gradient steps
-
give rigorous unitary synthesis for
- imaginary-time evolution
- quantum signal processing
- diagonalization unitaries
- Grover's algorithm is an approximation to imaginary-time evolution
J. Son
B. Tiang
S. Carrazza
R. Seidel
R. Zander
Z. Holmes
Y. Suzuki
Tell me when not fast enough? Get stuck? Something else?
Your input is needed to improve them!
N. Ng
What about other methods?
0
0
0
0
Universal gate set:
single qubit rotations + generic 2 qubit gate
Universal gate set can approximate any unitary
What is a universal quantum computer?
|\psi\rangle = U |00\ldots0\rangle
quantum compiling approximates unitaries with circuits
\Rightarrow U \approx U_c
Quantum compiling
2x2 unitary matrix - use Euler angles
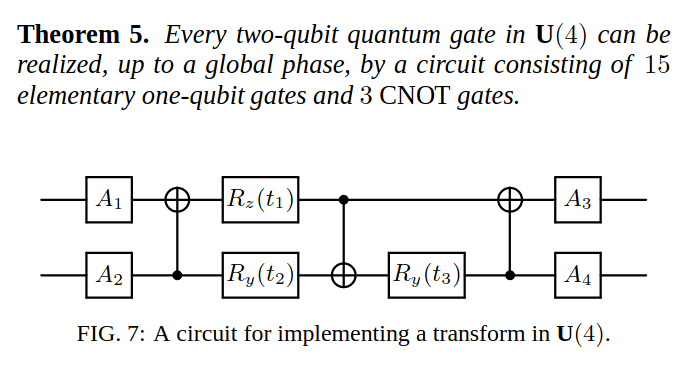
4x4 unitary matrix - use KAK decomposition + 3x CNOT formula
\text{CNOT} = |0\rangle\langle 0|\otimes \begin{pmatrix} 1 & 0\\ 0 &1\end{pmatrix}
+ |1\rangle\langle1 |\otimes \begin{pmatrix} 0 & 1\\ 1 &0\end{pmatrix}
=
2 qubit unitary
Canonical
KAK decomposition, Brockett's work etc
=
2 qubit unitaries modulo single qubit unitaries are a 3 dimensional torus
Quantum compiling
\(2\) qubits - \(4\times 4\) unitary matrix - use KAK decomposition + \(3\) CNOT formula
Quantum compiling
\(1\) qubit - \(2\times 2\) unitary matrix - use Euler angles
\(n\) qubits - \(2^n\) unitary matrix - use quantum Shannon decomposition + \(O(4^n)\) CNOT formula
Variational quantum eigensolver
0
0
0
0
+
+
+
+
+
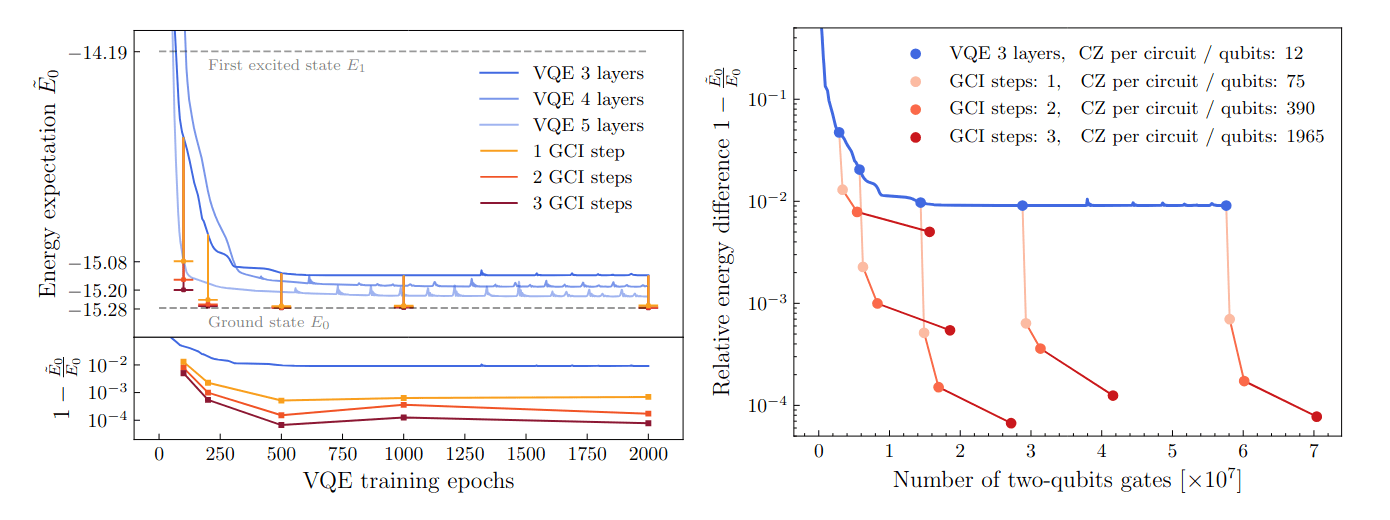
This works but is inefficient
This is efficient but doesn't work
Open: fill this gap!
\hat W_k = [\hat D_{k-1},\hat H_{k-1}]
\hat H_k = e^{s_k \hat W_k} \hat H_{k-1} e^{-s_k \hat W_k}
Double-bracket iteration
s_k
Rotation durations:
Input:
\hat H_0
\hat D_k
Diagonal generators:
A new approach to diagonalization on a quantum computer
Great: we can diagonalize
How to quantum compile?
Overview of double-bracket quantum algorithms
By Marek Gluza
